Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
SO Gladkov*
Received: November 27, 2023; Published: December 12, 2023
*Corresponding author: SO Gladkov, Moscow Aviation Institute (National Research University) (MAI), Volokolamskoe shosse, 4. 125993, Moscow, Russia
DOI: 10.26717/BJSTR.2023.54.008500
It has been strictly analytically proved that there is a possibility of an external low- frequency EM field and resonant acoustic field influence on oncological diseases so that to destroy the diseased cells of the body. A numerical estimate of the frequency range in which this is carried out is given.
Keywords: Low-Frequency EM Field; Acoustic Influence; Frequency Range
In previous author's works (see [1-3]) we investigated some individual cases of the manifestation of the body's reaction to the influence of external variables of electromagnetic (abbreviated – EM) fields. In this paper we will continue our research in this direction and try to answer the question of finding the frequency range in which the destruction of the affected cells is possible. In this message we will expand the search a bit and consider acoustic fields along with an alternating electric field. As we will see later there is a certain frequency range in reality when such a possibility is realizable. It is also worth noting that when any magnetic additives for example iron or manganese are artificially introduced into the body cell structure affected by oncology the reaction of these cells to the alternating magnetic field becomes much more effective. At the same time the same natural question arises: is it possible to find such a frequency range of the external alternating magnetic field so that the affected cells begin to collapse as well as in the result of exposure of the body to alternating electric and acoustic fields? It would be biased on our part not to say that work was carried out in this direction but in the vast majority it was purely experimental research. However, although a number of works are theoretical in nature (see for example [4-11]) the approach discussed below allows to find specific values of "therapeutic" frequencies. Further on we will focus on the study of the effects on the body of electric and acoustic fields only and we will not consider the magnetic field yet.
Consider this situation. Let a constant electric field E0 affect the body for a certain period of time Δt. Time Δt is defined as the time of occurrence of a polarizing moment p induced in each affected cell by a constant and uniform fieldE0. This means that if the body is additional exposed to the alternating field.

where E0 − is its amplitude and is w− the frequency the induced dipole moments dc will begin to oscillate. The lower indexindicates that we are talking about a diseased cell. The connection of the dipole moment vector with polarization as it is known [12] is determined in our case by the dependence.

where V0 − is the volume of one cell. Based on the motion equation ma=F where m− is the mass of the cellular matter exposed to the electric field and the force acting on it is determined by the expression

where q − is the charge induced by the field E0 in accordance with the dependence (1) we have
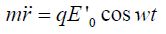
Integrating this equation twice over the time we find

where r0 − is one integration constant. The second constant is set to zero. It follows from (4) that the dipole moment according to the definition of [13] but in relation to our problem is
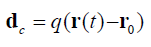
That is

Hence the internal energy of the cell resulting from the superposition of both electric fields based on the general definition of [12] namely E = −d⋅E according to (1) and (5) will be

Taking also into account the energy of the cell surface tension αc which should keep it from disintegrating the total energy taking into account (6) may be represented as

where Sc − is the total cell surface area. We will introduce the average density of the diseased cell Pc into consideration and we will consider it a sphere with radius Rc for simplicity. As a result, the total energy (7) may then be rewritten as follows:
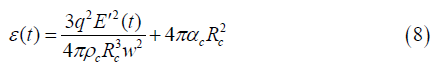
Where it was taken into account that the sphere area
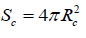
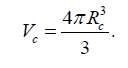
Further averaging the energy (8) over the oscillation period
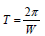

To find the full force acting inside the cell expression (9) should be differentiated by radius Rc. As a result, we
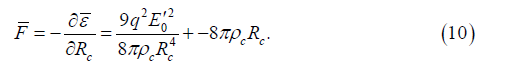
Based on the condition F ≥ 0 we find the threshold value of the frequency at which the cell destruction process should occur

Formula (11) answers the first question about the theoretical possibility of the external electric field influence on oncological diseases. Upper frequency threshold (right side in (11))
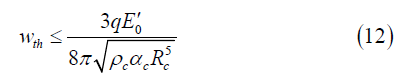
may be estimated based on the following numerical values of the parameters. The cell density may be set equal to the water density that is
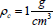
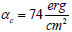
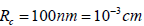
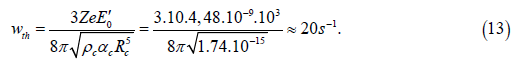
Such a frequency in the case of EM oscillations corresponds to approximately a kilometer wavelength range.
It is worth emphasizing that since both healthy and diseased cells are quite close in physical parameters great caution should be exercised here and it is necessary previously purely experimentally determine all the physical indicators of oncological and healthy cells. After that it will be possible to say quite definitely which specific frequency not affecting healthy cells should lead to the death of the diseased cells.
In order to assess the influence of an acoustic wave on the cell we will proceed as follows. Let ξ =ξ (x, y)- be the deviation of the cell surface points associated with an external acoustic influence from some of its average value Rc. As a simple approximation we will consider the cells to be ideal spheres of radius Rc. If the cell surface tension is denoted as αs(in dimension this is the energy attributed to the unit of its surface) and the surface density as Pcwhich is defined in the usual way in the form
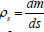
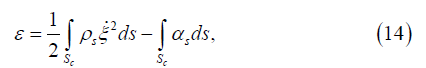
where
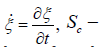
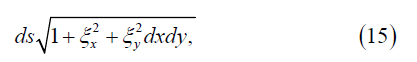
Where
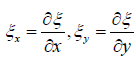
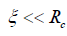
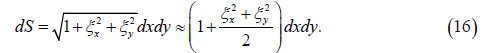
Omitting an insignificant constant, we write expression (14) taking into account (16) in a more general form assuming that the shiftis ξ a vector ξ
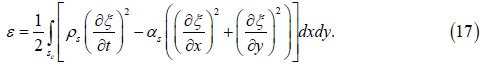
Finding the variation of functional (17) by ξ and setting it to zero we come to the equation

where
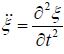
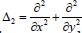
That is instead of (18) the equation should be written
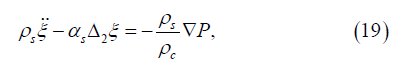
where ρc is the cell density.
Since
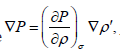
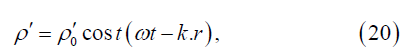
where ω − is the frequency, k − is the wave vector, ρ0′ − and is the amplitude of the sound wave we get from eq. (19)
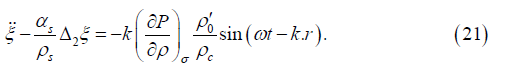
Choosing vector ξ in the radial direction and assuming that the wave inside the cell is homogeneous that is its length λ significantly exceeds the linear size of the cell Rc and this in turn allows to assume that the length of the wave vector may be represented in the form
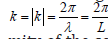
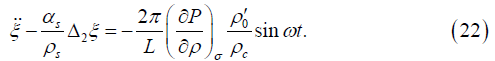
The partial derivative appearing here may be transformed as follows. We will proceed from the state equation of an ideal gas [8] according to which
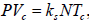

where mc− is the effective mass of the inner part of the cell. Based on the formula
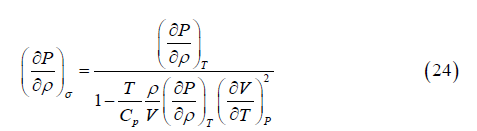
where Cp− is isobaric heat capacity taking into account the dependence (23) we obtain
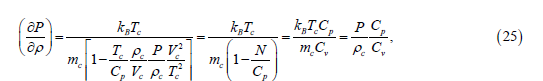
where Cv− is the isobaric heat capacity. For the cell we may assume that

Thus, according to (25) and condition (26) equation (22) may be rewritten as
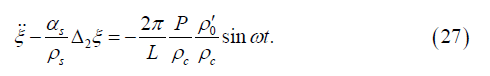
Further using the approximation
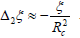
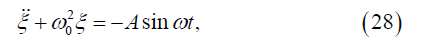
where the amplitude is
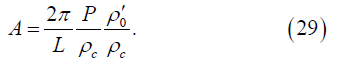
And the natural frequency of the cell surface oscillations
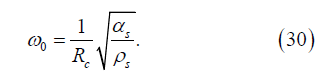
The resonant solution of equation (29) is found trivially and as a result we find
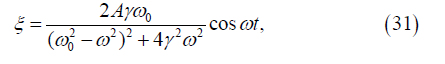
where we have formally introduced attenuation γ which must satisfy the condition

At resonance the wave amplitude appearing in solution (31) takes the value
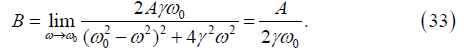
Let's estimate the values of frequency ω0 and amplitude B. According to (30) we have
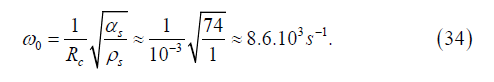
And according to (29) and (33) we get
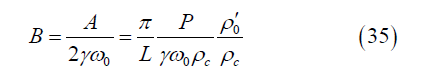
In the CGS system the pressure may be set equal to P =104 SGS . The attenuation based on the inequality (32) and the estimate (34) let be equal to γ =10s−1 . The length of the inhomogeneity may be set equal to the linear size of the cell that is L = 2Rc.
Thus, we will have from (35)
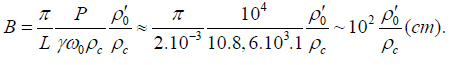
It may be seen that for a real ratio
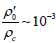
Concluding this message, we note.
1. It is shown that at a frequency close to the ultrasonic threshold (formula (30)) acoustic oscillations may well lead to the destruction of the diseased cells.
For the alternating electric field, the frequency must be extremely low, that is the EM wavelength is very large and that practically allows us to deem the applied electric field to be simply homogeneous.


