ABSTRACT
The mechanism of the electromagnetic field effect on the cellular structure of the body is considered in detail. It is shown that it is possible to take into account the interaction of both healthy and diseased cells with an external variable EM field, the electric component of which behaves according to a special time law, as well as the magnetic one. The mathematical model is based on a system of modified Lotka-Volterra and Verhulst equations, in which the coefficients are functions of time. It is shown that at the moment of time t = t1 there is a “switching” (as in the theory of optimal control) of the destruction mechanism to the reverse one, which should lead to the growth of healthy cells and the destruction of malignant ones.
Keywords: Electromagnetic Field; Predator-Prey Model; Nonlinear Differential Equations
Introduction
This work is a logical continuation of a series of previous works devoted to the analysis of the influence of external constant and variable electromagnetic (abbreviated as EM) fields on biological objects (see articles [1,2]). This report will focus on the study of the influence of variable EM fields on the cellular structure of the body. In this case, the system of the Lotka-Volterra equations [3,4] will be taken as the basis for calculations and estimates, which we will modify accordingly in relation to our problem, relying to a large extent also on the work [5]. It is not difficult to formally introduce any type of interaction into the system under study. The main issue is always the physical and mathematical justification of the appropriate type of interaction and understanding how to apply it to a particular task. It is this justification that we will now deal with in order to achieve this goal. It is worth noting beforehand that issues related to the mathematical description of cancer diseases have been dealt with for a relatively long time, and there are a number of results in this area, described in some detail, for example, in [6- 7]. The approach proposed below is based on considerations other than those mentioned above and gives a theoretical prediction for the treatment of such diseases.
The Energy of Cell Interaction with the EM Field
In order to find the interaction we are interested in, we will need to take into account the following two very important points. Namely, firstly, this interaction should be invariant with respect to the time sign inversion, and, secondly, it should take into account the concentration of “predators” and “preys”. In our case the role of predators will belong to cancer cells, the concentration of which we will designate with a letter n , and the role of the preys – to healthy cells; their concentration we will designate with a letterm . Note that we adhere to the same designations as in [5]. It is quite clear (see monograph [8]) that the interaction of any bodies with the EM fields can be different from zero only if the internal structure of the object under consideration allows to take into account its polarization p and magnetization m . However, if almost any object, including a cell, is under long-term exposure to constant EM fields, it will be certainly polarized. This means that, despite its extremely complex structure, there will be a slight deformation of the cell, which allows us to consider the polarization p . This means that we may take into account the possible interaction of cellular substance with a variable electric field E′(t ) , but only after the 0 E polarization of the cell is induced by the applied constant electric field. Such an interaction, attributed to a unit of volume, as it is known [8], formally has the form of a negative scalar product −p⋅E′ , where

Where αñ − is the cell polarization coefficient As for the magnetic field, if there are magnetic atoms in the cell structure in the form of, for example, iron, manganese or other magnetic particles, as well as moving charges, the energy of interaction with an external variable magnetic field will necessarily manifest itself H′(t ) in the same way as with an electric field, but already having the form of −m⋅H′(t ) where

This vector represents the magnetic moment of the cellular substance, χñ − is the magnetic susceptibility of the cell, and H0 − is the constant magnetic field applied to the body.
The account of interaction with the field will be given further phenomenological (see formulas (18), (19)) in the form of dependencies of coefficients b(t ) and c (t ) (see equations (5)).
Basic Equations and their Analysis
If we denote some average energy of the corresponding group of cells as 1,2 ε , then taking into account (3) and based on the results of [5], we can write the following expression for the functional we are interested in
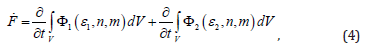
Where functions Φ1,2 (n,m) are given in [5], and their explicit form is not important for us now.
Using the general method of deriving equations proposed in [9], we arrive as a result at the following system of two nonlinear equations that adequately describes our case:
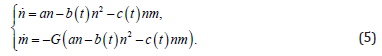
Where a − will be considered a constant parameter, and we will need functions b(t ) and c (t ) further below.
As we can see, if we assume that b(t ) = 0 in the upper equation, we get the generalized Lotka-Volterra equation [3], [4], in which coefficient c (t ) is a function of time. And if we believe that c (t ) = 0 , then we get the generalized Verhulst equation (see [5]), in which coefficient b(t ) is a function of time [10].
Equations (5) also automatically take into account the condition of preserving the total amount of cellular substance in the body, that is,

Where μ1,2 − the masses of one healthy and one cancer cell are, respectively, M − is the total mass of the cellular substance, and V − is the volume occupied by it.
Based on the ratio (6), it is easy to find the time dependencies n(t ) and m(t ) that we are interested in. Indeed, expressing one of them by equation (6), for example m(t ) , we have

Where

After substituting (7) into the upper equation of the system (5), we arrive to the following solution

Where 2 C − is the integration constant, and the function

Constant 2 C is found from the initial condition n(0) = n0 . As a result

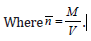
Substituting solution (9) into (7) now, we come to the following time dependence of the temporal behaviour of healthy cells:

As we can see from obtained solutions (9) and (12), the healthy and diseased cells behave quite adequately. Specifically, if the function is A(t ) = b(t ) −Gc (t ) > 0 , then the disease wins, because

In this case, the function A(t )must be such that condition (13) is fulfilled. As we can see from (9) and (12), in this case

And

At some point of “switching” function A(t ) = b(t ) −Gc (t ) changes sign, that is, it becomes negative ( A(t ) = b(t ) −Gc (t ) < 0 ) and we get the opposite picture. In this case, the disease recedes, and we come to equality

And healthy cells are restored, that is:

Now, as for the functions b(t ) andc (t ) . Due to the fact that the connection with the EM field has the form of a dipole interaction, then, based on purely physical considerations and the correct dimension of the equations, the form of these coefficients can only be as follows:


Where 1,2 a − the linear dimensions of diseased and healthy cells are, respectively, c S − is the contact area along the border line between them, and the dot above the letter means differentiation according to time.
Thus, function (10) of out interest, taking into account (1), (18) and (19), should be the following
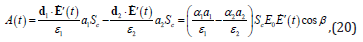
Where β − is the angle between the direction of the external constant field and vectorE ′(t ) .
As we can see from (20), when changing the direction of the polarity of the fields, function A(t ) must change the sign to the opposite. By doing this, we achieve the opposite effect, that is, following the theory proposed above, there will have to be the destruction of diseased cells and the growth of healthy ones.
In this case, we may express function E′(t ) , for example, in the form of a linear time dependence, that is

Where γ − is a certain growth coefficient.
The Main Idea of the Work
The general physical considerations outlined above concerning possible methods of combating malignant tumours (and not only them, but many other similar diseases), allow, in our opinion, to select such variable fields and their amplitudes, which, in the process of reversal magnetization of their directions, will certainly lead to a positive therapeutic result.
Conclusion
Concluding this message, it is worth paying attention to two important points. The influence of variable EM fields on the reproduction of malignant tumours has been studied; It is shown that the proposed model quite adequately describes both the growth and disappearance of cancer cells, that is, the recovery of the body.
References
- SO Gladkov (2019) On the possibility of detecting different kins of diseases with the help of fixation of electromagnetic radiation intensity of red blood cells. BJSTR 20(1): 14806-14808.
- SO Gladkov (2021) On the effect of the variable electromagnetic field on the movement of red blood cells on the circulatory system. BJSTR 36(3): 28477-28479.
- AJ Lotka (1925) Elements of Physical Biology (Williams & Wilkins, Baltimore).
- V Volterra (1926) Mem. Acad. Lince 6: 31-37.
- SO Gladkov (2021) On the question of self – organization of population dynamics on Earth. Biophysics 66(5): 858-866.
- A Rescigno, C De Lisi (1977) Immune surveillance and neoplasia II. Bull. Math. Biol 39: 487-497.
- GW Swan (1977) Some current mathematical topics in cancer research. Xerox University Microfilms, Ann Arbor, Michigan. MI.
- GW Swan (1979) Immunological surveillance and neoplastic development. Rocky Mountain J Math 9(1): 143-148.
- LD Landau, EM Lifshitz, LP Pitaevskii (1984) Electrodynamics of Continuous Media. M Nauka, pp. 620.
- SO Gladkov (2021) On a methodological approach to the derivation of basic physical equations. Physical Education in Universities 27(2): 5-12.

 Mini Review
Mini Review