Physical Model of the Method of Nutrition of Microorganisms Volume 51- Issue 3

Glushchenko AG*, Glushchenko AA and Glushchenko VA

• Department of Physics Povolzhsky State University of Telecommunications and Informatics, Russia

Received: June 30, 2023;   Published: July 10, 2023

*Corresponding author: Alexander Glushchenko, Department of Physics Povolzhsky State Uni-versity of Telecommunications and Informatics, Russia

DOI: 10.26717/BJSTR.2023.51.008103

Abstract PDF

Systems of interrelated oscillators determine the structure of a large number of natural materials. The interaction of oscillators leads to a change in their mode of oscillation, in particular, to synchronization of oscillations. In the present work, we consider the possibilities of another physical effect of the interaction of oscillators, which, when the oscillation frequency changes, leads to the movement of the interference pattern formed by the oscillators to a shift of the high-frequency oscillator towards a lower frequency one. It has been found that the presence of a shift in the frequencies of the oscillator radiation leads to their motion. This allows you to control the movement of one of the oscillators (prey) by changing the frequency of the radiation of the other oscillator (hunter) both in the direction of convergence and in the direction of removal of the oscillators. The conditions for the equilibrium state of a system of oscillators, which require the coherence of oscillators, are obtained.

Keywords: Quasi-Coherent Oscillators; Interaction; Stability; Motion Condition

In nature, an important property of all living organisms from higher to microorganisms are the organs of fixation of oscillatory processes - electromagnetic, acoustic, which allow communication with the external environment [1,2]. In each organism, the organs of perception of oscillations and waves are arranged in a certain way and have individual frequency characteristics for each type [3,4]. The purpose of these sensory organs is diverse, but they are usually associated with the method of communication (the emitted signals are a means for transmitting information), for orientation in the external environment (biolocation), for protection in the form of threat signals to enemies and competitors. Acoustic biosignals are the most studied, it is known that all living organisms, including protozoa, for example, microbes and insects, can make sounds of different frequencies and different timbres, which can change. Here we consider another possibility of using electrical high-frequency signals by bioorganisms and the reason for the continuous supply of signals (close to monochromatic) by the simplest organisms. A possible reason for the regular emission of such signals is the force impact of some organisms on others due to the physical effect of mutual attraction of oscillators (in this case, biooscillators) with similar frequencies. Thus, one observes (by adjusting the radiation frequency) the absorption by some organisms of other, smaller ones (food or an electric method of hunting). It has been established that the immobility or randomness of the movement of the simplest organisms is only apparent. In fact, with their radiation, organisms create an interference pattern controlled by the frequency of the radiation of the hunter, at the minimum of which prey falls, which is affected by an attractive or repulsive force field.

Consider the interaction of two bioorganisms as the interaction of two quasi-coherent oscillators with radiation frequencies 𝜔 and 𝜔+Δ𝜔, under the condition (Δ𝜔<<𝜔) [5,6]. We study the interaction of stationary charges in the form of harmonic oscillators with Coulomb coupling located at a distance r from each other charges. The interaction of charges is described by Coulomb’s law.

The force acting on the second oscillator from the first oscillator has the form:

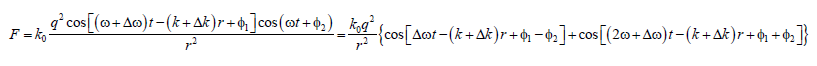
The first term describes the force that determines the position of a stable equilibrium of oscillators. When the condition

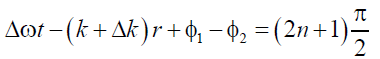
this force is zero at the points defined by the expression (stable equilibrium) that move in time at a speed in the direction of an oscillator with a lower frequency ( ω₂ < ω₁ ). Thus, the frequency difference of the oscillators, leading to a linear change in time of the phase difference of the oscillators ( Δφ = Δωt ) leads to the movement of the system of oscillators in the direction of oscillators with a lower frequency (to the region of stable equilibrium). The second term in characterizes the wave with the frequency 2ω created by the first oscillator in the region where the second oscillator is located. If ( Δω = 0 ), then the system is in a stable stationary state, at ( Δω ≠ 0 ) , the system of oscillators will move in the direction of the stable position of the oscillators, which also moves at a constant speed determined by the frequency difference of the oscillators. Changing the oscillation frequency of one of the oscillators of the system sets the system in motion in the direction of the oscillator with a lower oscillation frequency. Thus, by controlling the oscillation frequency of one of the oscillators, it is possible to cause the system to move (towards the oscillator with a lower oscillation frequency) until the oscillation frequencies differ A change in the frequency of an oscillator can, as in mechanical oscillators, be associated with the value of its mass, i.e. a more massive oscillator may have oscillation frequencies lower than those of other oscillators and thus be an “attraction” region.

It has been established that in addition to the well-known tasks of communication of biological organisms, there is another important function of oscillation used by insects - food, due to the interaction of oscillations, they can physically capture the biooscillator using the described wave process to form a moving wave potential well into which the prey of the biooscillator falls. The mismatch of oscillation frequencies controlled by one of the bioorganisms leads to the movement of the system in the direction of oscillators with a lower oscillation frequency. A physical model of the interaction of two quasi-coherent oscillators that form the interference pattern of the force field is considered, of which one (fixed) is the main source of radiation, the second, unfixed, is located in the interference minimum zone, which, depending on the phases and frequencies of the emitters, can be mobile and cause movement oscillator. More complex combinations of interacting oscillators are considered.

1. https://slidetodoc.com/communication-in-insects-contents-introduction-types-of-insect/.
2. Kaupp UB (2010) Olfactory signalling in vertebrates and insects: differences and commonalities. NATURE REVIEWS | Neuroscience11: 188-200.
3. Wilson BYR (2022) Experiments show by reprogramming the electrical communication between cells, organisms grow extra limbs, eyes and heads.
4. Glushchenko AG, Glushchenko EP, Glushchenko AA (2020) Low Frequency Electromagnetic Radiation Effect Through the Ionosphere. Biomed J Sci & Tech Res 29(2).
5. Csaba G, Porod W (2020) Coupled oscillators for computing: A review and perspective. Applied Physics Reviews 7: 011302.
6. Westra JR, Chris JM Verhoeven A, Roermund HM (1997) Oscillators and Oscillator Systems: Classification, Analysis and Synthesis. N.Y 277.