Abstract
Model parameter selection in the process of mathematical modeling is a formidable problem which requires sophisticated algorithm indexed by a Matlab random generation function having a dominant 0.01 intensity with very few instances of higher random intensity for obvious reasons. This study have utilized the Matlab algorithm with a random function of order ten (10) having the structure: v = m+0.01 times rand(10) with this random generation function. The novel result obtained shows boundary values of each parameter estimate, and have proven clearly why we have chosen our present model parameter values for the case of Port Harcourt HIV infection public health data that defines the number of target cells, number of infected cells, and number of viral load of the virions for every 30 day simplification for the purpose of HIV intervention strategy.
Keywords: Mathematical Modeling; Parameter Selection; Random Generation function; Matlab Algorithm; Numerical simulation
Introduction
Parameter estimation problem being an integral aspect of mathematical modeling has been a long standing problem [1-3]. However, there is urgent need to specify one of the alternatives of determining the estimated parameter values with particular reference with the modeling of HIV infection of CD4+ T- cells. In fast developing country like Nigeria where public health data are in acute shortage for purpose of designing a database that can be useful in the intervention of HIV infection, it is worthwhile to implement and apply this present numerical approach for the purpose of a numerical characterization of a time dependent viral load of the virions with the insight of forming HIV infection intervention database for the city of Port Harcourt in Nigeria. The factors that define the depletion of viral load of the virions over time and those that increase the viral load over time can provide useful insight for the intervention of this public health concerns. Some of the challenging and salient businesses of modelers in mathematical immunology are to develop models, methods of analysis and control of the immune system processes [4-6]. Starting with the classic research of Nwagor P et al. [7-9], on immune system modeling and HIV-infection; this research in same vein also intends to examine further certain other properties of the already solved dynamic model which includes parameter estimation representing the HIV-infectio P n.
Time Dependent ODE Model
Following Nwagor (2020). A system of time dependent nonlinear first ordinary differential equations is considered. In the absence of the delay term with τ=0 then the model reduces to
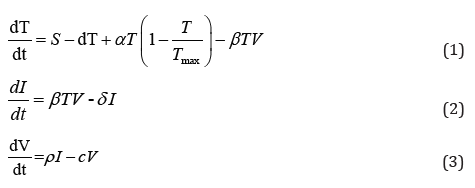
Where the notations T represents the number of target cells, I represent the number of infected cells, V represents the viral load of the virions at time t in units of days, s represents the rate at which the new T cells are created from the source within the body such as the thymus, a represents the maximum proliferation rate of target cells. Tmax represents the T population density at which proliferation shuts off, d represents the death rate of the T cells. β represents the infection rate, δ represents the death rate of infective cells, ρ represents the rate of cure, c is the clearance rate constant of virions. The positive integer τ represents length of time measured in days. The system (1)-(3) satisfies the initial condition
T(0) ≥ 0, I (0) ≥ 0,V (0) ≥ 0
The possible non negative equilibrium of the system are E1( To,0,0) E2( T*, I*,V* )
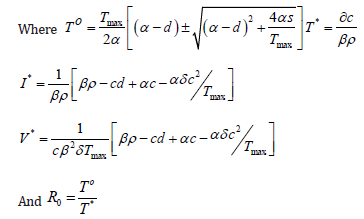
Where R0 defines the basic reproductive ratio, which determines the dynamical property of the system (1 - 3) over a long period of time.
MATLAB Numerical Scheme
The theory of MATLAB numerical scheme considered in this study involves the two-point boundary value problem of the equations of the form.
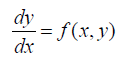
Subject to the initial condition
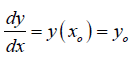
by increasing each step-in x by h, so that the nth step becomes
xn = x0 + nh
The Euler algorithm for the determination of the approximation
yn+1 to y(xn+1) is yn+1= yn+ f( xn, yn )h
The modified Euler method involves taking the gradient of the tangent line approximation at (xn, yn) n n x y the average of the gradient
(xn, yn ) and (xn+1, yn+1)
so that the algorithm for the modified Euler for the determination of approximation is given by
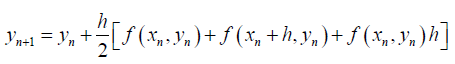
Also, the Runge-Kutta method which is based on a Taylor series approximation to the function f(x,y) defines its algorithm for the determination of the approximation
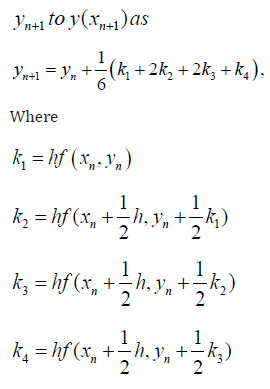
The Runge-Kutta method also extends to the solution of the problem of the type
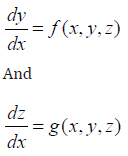
Subject to the initial conditions
y (x0) = y0 z(x0 )= z0
For a step of length h, and the nth integration step, the Runge- Kutta algorithm for systems is of the form
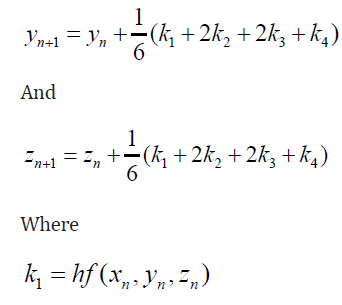
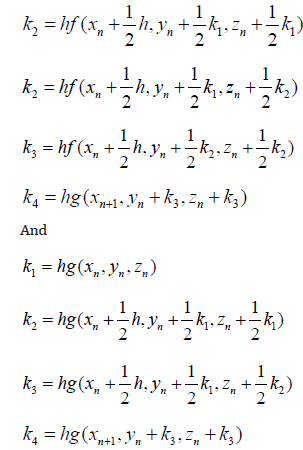
Hence, therefore the error (local) involved in the determination of yn+1 from y0 and zn+1 from z0 is 0(h5 ) as with Runge-Kutta method. (Jeffery and Dai, 2006 in Nwagor 2019)
Materials and Methods
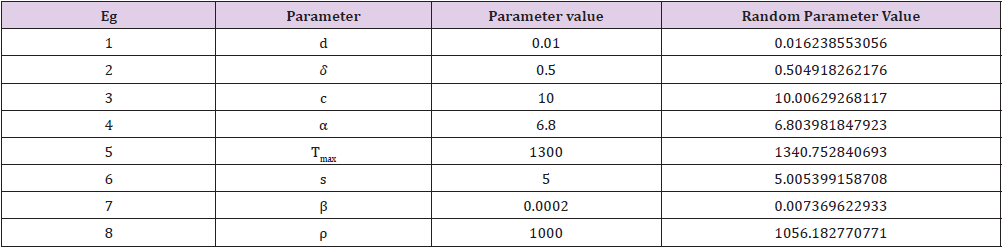
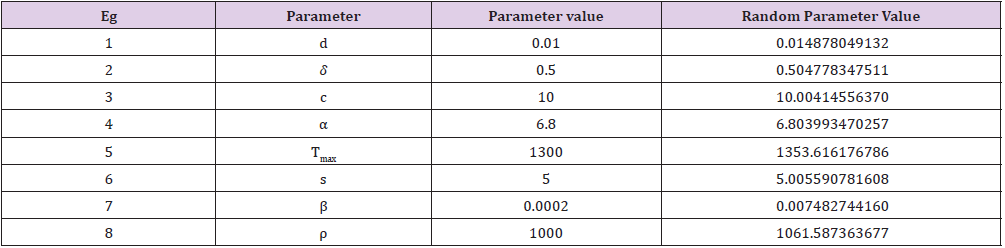
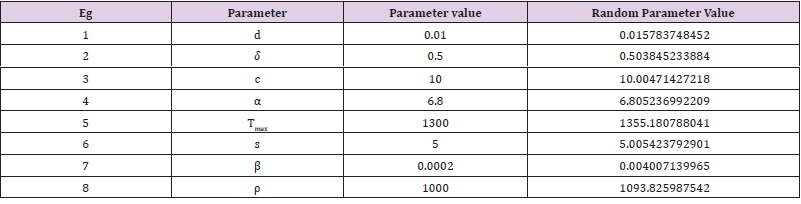
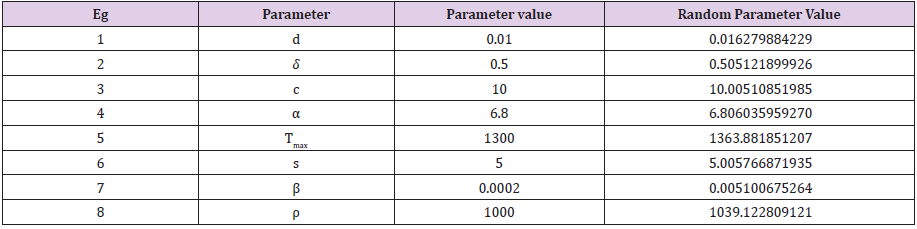
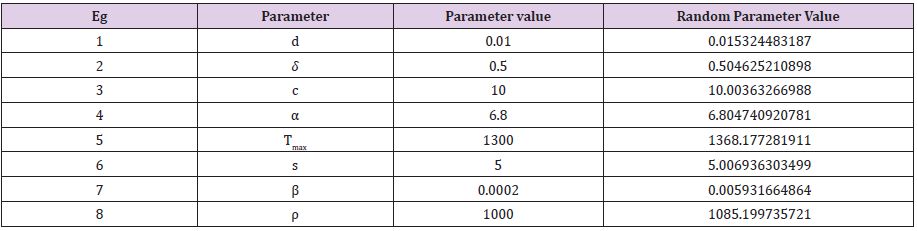
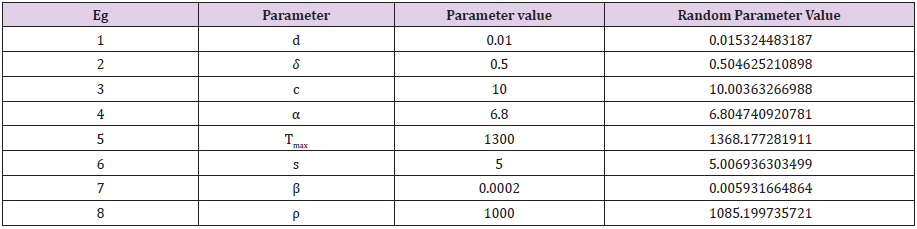
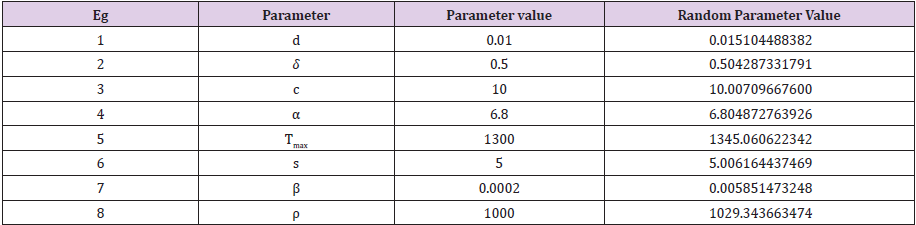
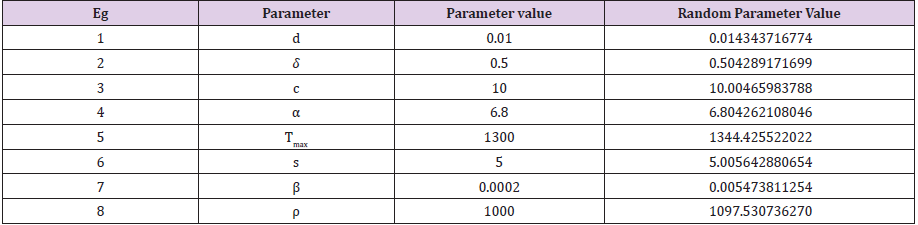
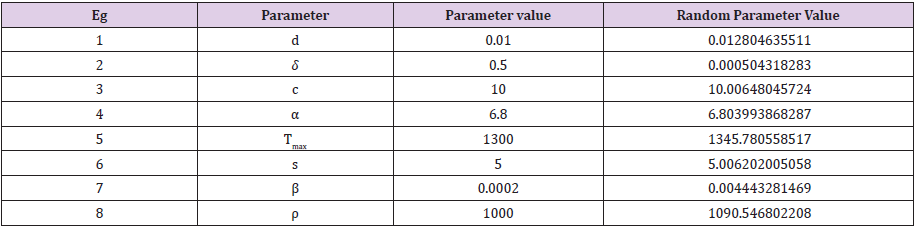
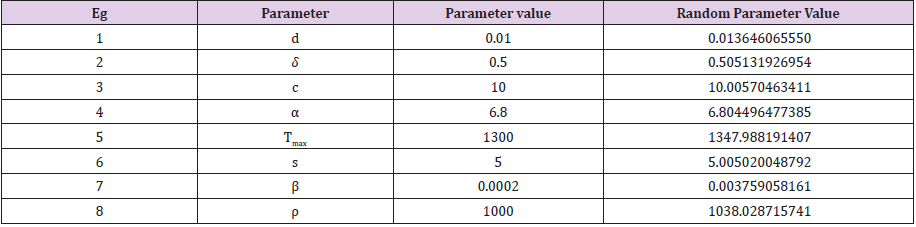
In this study, if m represents a specified model parameter value that contributes to growth of targets cells, the growth of infected cells, and the growth of the viral load of the virions. We have utilized the following Matlab algorithm using a random function of order ten (10) having the following structure: v = m+0.01 times and(10) with this random generation function we are able to prove that the following that the following model parameter values of
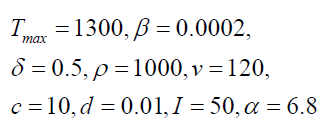
clearly satisfy a mathematical upper bound definition. This key assumption makes sense while the Port Harcourt HIV public health data should be considered as the best, minimum values in the context of modeling the characterization of a time dependent viral load of the virions.
Results
In The results of this study are presented as shown in Tables 1-10.
Table 1: Parameter selection using Random generation function indexed by Matlab algorithm of order 10; scenario 1.
Table 2: Parameter selection using Random generation function indexed by Matlab algorithm of order 10; scenario 2.
Table 3: Parameter selection using Random generation function indexed by Matlab algorithm of order 10; scenario 3.
Table 4: Parameter selection using Random generation function indexed by Matlab algorithm of order 10; scenario 4.
Table 5: Parameter selection using Random generation function indexed by Matlab algorithm of order 10; scenario 5.
Table 6: Parameter selection using Random generation function indexed by Matlab algorithm of order 10; scenario 6.
Table 7: Parameter selection using Random generation function indexed by Matlab algorithm of order 10; scenario 7.
Table 8: Parameter selection using Random generation function indexed by Matlab algorithm of order 10; scenario 8.
Table 9: Parameter selection using Random generation function indexed by Matlab algorithm of order 10; scenario 9.
Table 10: Parameter selection using Random generation function indexed by Matlab algorithm of order 10; scenario 10.
Discussion of Results
From Tables 1-10, it is observed that each model parameter
value is strictly bounded above by its least upper bound which
clearly shows that the choice of the model parameter values is the
minimum for each range such as o This study work have successfully utilized a Matlab function
algorithm to conduct a systematic random generation of HIV
infection model parameter values from which the choice of nonstochastic
parameter values can be deduced as the minimum
estimated values in this context. A future investigation will attempt
to look at error analysis on the difference between pairs of such
random generated data.Conclusion and Further Research
References

 Short Communication
Short Communication