Malaria and Other Infectious Diseases, Suppression of the Evolution of Drug Resistance Volume 12 - Issue 2

Alan Kleinman*

• Primary Care Physician and An Engineer, California, USA

Received:December 05, 2018;   Published: December 17, 2018

*Corresponding author: Alan Kleinman, Primary Care Physician and An Engineer, California, USA

DOI: 10.26717/BJSTR.2018.12.002219

Abstract PDF

It is well understood that combination therapy suppresses the evolution of drug resistance. The number of drugs necessary to do this depends on many factors. This paper addresses the key factors in the context of a treatment protocol for malaria which still saw the emergence of resistance despite the use of combination therapy. This paper gives general guidance on the principles of determining the kind and number of selection pressures needed to suppress the evolution of drug resistance.

Keywords: Evolution; Drug Resistance; Suppression; Combination Therapy; Immune Competence; Susceptibility

Any attempt to use selection pressures to control infectious diseases (or cancers as well) requires an understanding of how the selection pressure(s) work, the environment in which the selection pressures are operating and how the population is altered by the selection pressures in order to suppress the evolution of drug resistance. The treatment of malaria provides a good example of how these principles operate. Any durable treatment for infectious diseases should give a high probability of driving the infectious agent to extinction. That calculation needs to take into account the number of effective selection pressures, the environment (the patients) in which the selection pressures are operating and the population on which the selection pressures are acting.

Rogers et al in their paper “Failure of artesunate-mefloquine combination therapy for uncomplicated Plasmodium falciparum malaria in southern Cambodia” [1] gives a good model for explaining how and why drug resistance occurs. It has long been argued that combination therapy should give durable treatment for malaria in the same manner that combination therapy has given for the treatment of HIV [2]. The effectiveness of combination therapy for the treatment of infectious diseases and cancer was understood more than half a century ago by Edward Tatum which he wrote about this in his Nobel Laureate Lecture in 1958 [3]. But how many drugs in the combination therapy? Why three drugs with HIV and not two? How many selection pressures are needed to suppress the random mutation and natural selection phenomenon (rmns)? What are the variables which determine the number of selection pressures needed to suppress rmns and why?

Rogers and his co-authors describe possible reasons in their study. In their discussion on the failure of combination therapy, they describe some possible explanations. These include defective drugs in one form or another (unlikely), insufficient minimum inhibitory concentrations, preexisting resistance to one or the other drug effectively reducing the treatment to single drug therapy among these reasons. Two possible explanations for the emergence of resistance not considered in this paper are de novo evolution of resistance to the simultaneous use of both drugs and an analysis of those subjects in which the double drug resistant variants appeared.

The de novo evolution of drug resistance by rmns is discussed in [4,5]. Though in the Rogers study they do not include subjects with hyperparasitemia (250,000 parasites/mm3), 100,000 parasites/mm3 still gives rise to huge population sizes which were the upper limit used in the study. In [1] it is shown that with the huge population sizes attainable by malaria, there is a reasonable probability of a double beneficial mutation occurring which would be the mechanism for defeating two-drug therapy. To get an understanding of how combination therapy impacts the ability of a microbial population to adapt to these combination selection pressures, consider the following Venn diagram graphical representation of the mathematical behavior of the process (Figures 1-3).

Figure 1: Single drug treatment, the area inside the ellipse represents variant resistant to drug A1.

Figure 2:Two drug combination treatment, the area inside ellipse A1 represents variants resistant to drug A1. The area inside ellipse A2 represents the variants resistance to drug A2. The intersection of the two ellipses (the shaded area) represents the variants resistant to both drugs A1 and A2.

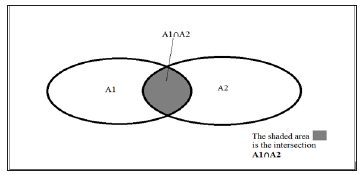
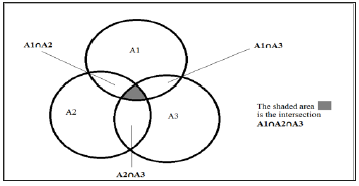
Figure 3:Three drug combination treatment, the area inside ellipse A1 represents variants resistant to drug A1. The area inside ellipse A2 represents the variants resistance to drug A2. The area inside ellipse A3 represents the variants resistance to drug A3. The intersection of the three ellipses (the shaded area) represents the variants resistant to all three drugs A1 and A2 and A3.

What these three Venn diagrams illustrate is the fraction of the malaria population which has some degree of resistance to the particular therapy. Consider what happens when one uses an antimicrobial drug to treat an infection. The drug acts by killing (or impairing the replication) of the weakest variants first. If the agent is effective against all the variants, given enough time of application of the drug (selection pressure), this will drive the microbe population to extinction. If there are variants in the population which have some resistance to the agent, successful treatment may still occur if the patient has adequate immune function to remove the remaining variants. If the patient’s immune system does not mount an adequate response, relapse occurs with variants that have some degree of resistance to that drug and if these variants can replicate sufficiently, there is the potential of more beneficial mutations for that microbe to improve fitness against that drug.

Using two drugs simultaneously reduces the fraction of the population of variants which have resistance to both drugs simultaneously. This smaller residual population of multi-drug resistant variants put a smaller load on the patient’s immune system but still, if the patient’s immune system cannot remove these variants, these remaining variants become candidates for more beneficial mutations getting resistance to both drugs simultaneously. However, unlike single drug therapy which only requires a sequence of single beneficial mutations to achieve resistance, double-drug therapy will require a sequence of doublebeneficial mutations to achieve resistance to the combination of drugs. This requires much larger populations of the infectious microbe but replicators like HIV and malaria can achieve these population sizes.

Three drug therapy follows the same pattern. In this case, though, the sub-population which is resistant to all three drugs will be much, much smaller than for either one or two drug therapy. If there happen to be some variants resistant to all three drugs, this will be a much smaller burden on the patient’s immune system but will also require three simultaneous mutations to continue to improve fitness. The population sizes required for this to occur are much larger than even HIV can attain. But patient compliance is a crucial factor in these situations. If a variant exists with resistance to the three drugs, even a short withdrawal of the selection pressures will allow the population to expand rapidly giving an improved probability of a simultaneous triple mutation improving fitness against these drugs.

The factor not considered in the Rogers study is the immune status of the subjects treated. The immune system is a very potent selection pressure on infections. There are people who survive malaria without treatment, even those without G6PD deficiency, thalassemia, and sickle cell red blood cell defects. There is extensive evidence of the importance of a functioning immune system in fighting disease. The ability of the immune system to fight disease is affected by many different variables. One could start with the very young and the very old who have an immature immune system and an aging immune system respectively. Comorbidities contribute to a poorly functioning immune system such as cancers, diabetes, etc. Malnourishment is an important factor in the functioning of the immune system. Medications which suppress the immune system such as steroids, drugs used to prevent organ rejection and drugs used to treat autoimmune diseases as well are important factors in determining the reason for the failure of a treatment of an infectious disease. Typical examples of how the immune status of patients impacts the evolution of drug resistance is given in references [6,7].

If one considers the three illustrations above in the context of the subject’s immune status, it becomes clear that single drug therapy imposes a greater burden on the subject’s immune system to defeat the malaria infection. Each additional drug used lowers that burden on the subject’s immune system. The parasite load will be much larger with single drug therapy than with two drug therapy. And the parasite load will be much larger with two drug therapy than with three-drug therapy. The mathematics which governs this relationship is given in [3]. Essentially, a patient with a totally compromised immune system would have the same response to treatment of their disease as in vitro lab testing would give.

Any treatment of an infectious disease must take all these factors into account. Even under ideal circumstances and proper use of medications, the existence of variants within the microbial population may require more than two drugs to ensure that the microbial population is driven to extinction (or prevented from accumulating the mutations which would give resistance to the treatment). Any general protocol to treat a particular infectious disease must start with the assumption that some patients will not be able to mount a reasonable immune response to the disease. And then a study of susceptibility patterns in the region will give guidance on which drugs have a reasonable chance of being effective in the set of selection pressures used to treat the disease.

1. Rogers WO, Sem R, Tero T, Chim P, Lim P, et al. (2009) Failure of artesunatemefloquine combination therapy for uncomplicated Plasmodium falciparum malaria in southern Cambodia. Malaria Journal 8: 10.
2. François Nosten, Philippe Brasseur (2002) Combination Therapy for Malaria. Drugs 62(9): 1315-1329.
3. Edward Tatum (1958) Nobel Laureate Lecture.
4. Kleinman A (2014) The basic science and mathematics of random mutation and natural selection. Statistics in Medicine 33(29): 5074- 5080
5. Kleinman A (2016) The mathematics of random mutation and natural selection for multiple simultaneous selection pressures and the evolution of antimicrobial drug resistance. Stat Med 35(29): 5391-5400.
6. Rahman MM, Khan MA (2009) Levofloxacin prophylaxis to prevent bacterial infection in chemotherapy-induced neutropenia in acute leukemia. Bangladesh Med Res Counc Bull 35(3): 91-94.
7. Kristyn E Yemm, Jason N Barreto, Ross A Dierkhising, Kristin C Mara, Naseema Gangat, et al. (2016) A Comparison of Levofloxacin and Oral Third Generation Cephalosporins As Antibacterial Prophylaxis in Acute Myeloid Leukemia (AML) during Chemotherapy-Induced Neutropenia. Blood 128: 3986.