Measuring the Strength of the Evidence Volume 6 - Issue 4

David Trafimow*¹ and Michiel de Boer²

• ¹Department of Psychology, New Mexico State University, Mexico
• ²Department of Health Sciences,VrijeUniversiteit Amsterdam, Netherlands

Received: June 02, 2018;   Published: July 11, 2018

*Corresponding author: AV Belousov,Physics Department, MV Lomonosov Moscow State University, Moscow, Russia

DOI: 10.26717/BJSTR.2018.06.001384

Abstract PDF

Many proponents of p-values assert that they measure the strength of the evidence with respect to a hypothesis. Many proponents of Bayes Factors assert that they measure the relative strength of the evidence with respect to competing hypotheses. From a philosophical perspective, both assertions are problematic because the strength of the evidence depends on auxiliary assumptions, whose worth is not quantifiable by p-values or Bayes Factors. In addition, from a measurement perspective, p-values and Bayes Factors fail to fulfill a basic measurement criterion for validity. For both classes of reasons, p-values and Bayes Factors do not validly measure the strength of the evidence.

Keywords: P-Value; Bayes Factor; Strength of the Evidence; Auxiliary Assumption; Reliability; Validity

Many researchers, statisticians, and mathematicians have suggested that the probability of a finding (or one more extreme), given a hypothesis (the familiar p-value), can be used as a measure of the strength of the evidence provided by that finding. In fact, no less an authority than Ronald Fisher argued that position (e.g., 1925; 1973) [1]. Although Bayesians eschew p-values, they favor Bayes Factors, which also concern probabilities of findings given hypotheses. To compute a Bayes Factor, one divides the probability of the finding given one hypothesis, by the probability of the finding given a competing hypothesis. Although there are many differences between aficionados of p-values and aficionados of Bayes Factors, both camps share a basic assumption, which is that the strength of the evidence can be captured by conditional probabilities of data given hypotheses. Our goal is to question this widely held assumption. We present two categories of arguments. The first category contains arguments based on philosophical considerations. The second category pertains to the specific issue of measurement, and whether conditional probabilities fulfill basic measurement requirements.

A long-known but underappreciated aspect of theory testing is that scientific theories contain nono bservational terms. Consider Newton’s famous equation:force=mass.acceleration As Nobel Laureate Leon Lederman [2] indicated, these are non observational terms. Even mass is a non observational term that should not be confused with weight, an observational term. The difference becomes obvious upon considering that the same object would have the same mass on Earth or Jupiter, but would have different weights on the two planets. To make the connection between mass and weight, it is necessary to have auxiliary assumptions, that relate mass to weight on the planets of interest. In general, researchers who wish to test theories attempt either to falsify or verify them. In either case, it is necessary to address the fact that theories contain non observational terms. Somehow, non observational terms in theories must be brought down to the level of observation, to enable researchers to perform theory tests. This is accomplished by combining the theory with auxiliary assumptions, to derive empirical hypotheses with observational terms. Because, in contrast to theories, empirical hypotheses have observational terms, they are amenable to testing.

Let us consider the traditional falsification perspective [3]. A naïve view might be that a single contrary finding disconfirms the theory, by the logic of as Lakatos [4] stated particularly clearly, a problem with this naïve view is that it starts from a premise that the empirical hypothesis derives from the theory, and only from the theory. But we have seen that empirical hypotheses derive from combinations of theories and auxiliary assumptions used to obtain observational terms in empirical hypotheses. As a logical matter, an empirical defeat disconfirms the conjunction of the theory and the auxiliary assumptions, which means that either the theory or the auxiliary assumptions (or both) are disconfirmed. There is no logically valid way to determine which alternative is the case, and as Duhem [5] and Lakatos [4] discussed in detail, it often is not straightforward to make the determination in practice.

Nor does coming at auxiliary assumptions from a verificationist position help much. As the cliché has it, empirical victories do not prove theories to be true because of the logical fallacy of affirming the consequent. For a chemistry example, phlogiston theory made some correct predictions, but the predictions worked for reasons other than the truth of phlogiston theory, as Lavoisier eventually demonstrated. The main problem in this case was not auxiliary assumptions (though there were problems there too that Lavoisier fixed) but rather that empirical victories fail to provide a valid proof of the theory they were designed to serve, as they could occur for a reason other than the theory. Of course, modern researchers are aware of this, but nevertheless insist that empirical victories increase the probabilities of the theories they serve. Under the condition that auxiliary assumptions are ignored, this latter insistence is valid. However, if auxiliary assumptions are considered, Trafimow [6] has provided detailed analyses showing that empirical victories can increase or decrease theory probabilities.

The latter may seem non intuitive, but an example might be the death-thought-suppression-and-rebound assumption that is an auxiliary assumption of terror management theory in social psychology. The problem is that most terror management theory predictions only work when there is a delay between making mortality salient and a wide variety of dependent variables. The death-thought-suppression-and-rebound assumption is that people suppress mortality salience initially, but it rebounds to become much more important during a delay. Thus, because of the rebound, making mortality salient works well after a delay but does not work well without a delay. Thus, using this auxiliary assumption, the fact that terror management theory effects work well when there is a delay, but do not work well when there is no delay, seems to strongly support terror management theory. However, Trafimow and Hughes [7] showed this auxiliary assumption to be wrong; mortality salience is greater when there is no delay than when there is a delay. Therefore, terror management theory effects should work best when there is no delay, rather than when there is a delay-the exact opposite of what is found in the voluminous literature on terror management theory findings.

The poorness of the auxiliary assumption rendered previous evidence allegedly favoring the theory instead to strongly militate against it. None of this is to say that researchers should not try for empirical victories for theories they wish to support, or for empirical defeats for theories they wish to disconfirm, only that the strength of the evidence such empirical victories or defeats provide depends heavily on the worth of the auxiliary assumptions used to derive empirical predictions from theories. Neither p-values nor Bayes Factors measure the worth of these auxiliary assumptions, and therefore cannot provide a good measure of the strength of the evidence. To see clearly that neither p-values nor Bayes Factors can measure the worth of auxiliary assumptions, consider an example where a researcher is interested in whether attitudes cause behavioral intentions. Attitudes and behavioral intentions are non observational terms, so it is necessary to make auxiliary assumptions to bring attitudes down to the level of a manipulation (e.g., that the persuasive essay used in an experiment really does manipulate relevant attitudes) and to bring behavioral intentions down to the level of a measure (e.g., that the items used in the behavioral intention scale really measure relevant behavioral intentions).

Note that the essay used and the items used are reasonably observable, as they can be read by anyone with passable vision who knows the language. Additional auxiliary assumptions might be that the sample used is randomly sampled from the population of interest, the randomization process is successful, a large assortment of nuisance factors does not matter (e.g., the time of day does not matter, the color of the experimenter’s clothing does not matter, and so on), and many others. Clearly, the worth of auxiliary assumptions is crucial for the strength of the evidence, yet p-values and Bayes Factors are incapable of measuring their worth. But perhaps an argument can be made in a more sophisticated way. For example, Chow [8] has suggested that theory testing can be considered in a cascading manner. There is a theory to be brought down to the level of an empirical hypothesis. In turn, the empirical hypothesis needs to be brought down to the level of a statisotical hypothesis. The statistical hypothesis, though far from definitive, is a necessary precursor to testing the theory. Thus, if one believes that p-values or Bayes Factors do a good job of measuring the strength of the evidence with respect to statistical hypotheses, they might be said to have value with respect to assessing the strength of the evidence more broadly.

As will become clear in the following section, p-values and Bayes Factors fail to meet standard measurement criteria. Therefore, they are not good measures of the strength of the evidence, even with respect to statistical hypotheses (never mind empirical hypotheses or theories). But for the present, let us accept the wrong premise anyhow. Returning to the example of attitudes causing behavioral intentions, suppose the researcher performs an experiment using a persuasive essay to manipulate attitudes and anticipates an effect on behavioral intentions, measured using items on a behavioral intention scale. The empirical hypothesis is that randomly assigning participants to read or not read the persuasive essay, should influence scores on the behavioral intention scale. The statistical hypothesis is that the population mean for the behavioral intention scale in the persuasive essay condition is greater than the population mean for the behavioral intention scale in the control condition. Note how far the statistical hypothesis is not only from the empirical hypothesis, but especially from the base theory that attitudes cause behavioral intentions.

Worse yet, the researcher who computes a p-value does not even test the researcher’s statistical hypothesis, because the p-value is based on the null hypothesis that the populations for the two conditions are the same. We emphasize that the null hypothesis is not the researcher’s statistical hypothesis, but rather a different statistical hypothesis. The poorness of the logic in making inferences about the researcher’s statistical hypothesis, based on a p-value testing the null hypothesis, has been covered by many others and need not be elaborated here. Let us pause and summarize. There is a theory with non observational terms and auxiliary assumptions are used to bring it down to the observational level expressed via an empirical hypothesis. In turn, the empirical hypothesis is transformed into a statistical hypothesis for increasing specificity. But the researcher who computes a p-value does not even test the statistical hypothesis. Instead, she tests the null hypothesis. Thus, she does not measure the strength of the evidence for her statistical hypothesis, nor her empirical hypothesis, nor her theory. A counter argument might be that the researcher could specify a range hypothesis that is closer to the researcher’s actual empirical hypothesis, and a one-tailed p-value can be computed based on the range [9,10].

An obvious problem here is that there is no way to calculate the probability of the finding, given a range null hypothesis, unless one knows the prior probability distribution. The Bayesian way around this problem is to impose an arbitrary or subjective prior probability distribution, and integrate across it; whereas the NHST way is to maximize [11]. Maximization has the advantage of guaranteeing that the resulting p-value is not smaller than it should be, but maximization has the disadvantage that the resulting p-value may be slightly larger than it should be, or immensely larger than it should be, or anywhere in between. If the goal were to control the Type I error rate, maximization might make sense because the researcher could be assured of not committing a Type I error more than 5% of the time; however, the present issue is not about Type I error but rather about using p-values to measure the strength of the evidence. Because the researcher who maximizes has no way of knowing how far off she is from the true value, it is immediately obvious that p-values for range null hypotheses fail to validly measure the strength of the evidence. Maximizing constitutes an admission that one does not have a precise measure of the strength of the evidence.

What about Bayes Factors? In some ways, Bayes Factors are superior to p-values. For example, suppose that one obtains p = .05. There is no logical way to make an inverse inference about the probability of the null hypothesis, given that p = .05, and so the p-value is not particularly useful. According to Kass and Raftery [11], the probability of the data given a hypothesis is useless information if one does not know the probability of the data with respect to a competing hypothesis. In contrast, a Bayes Factor gives the probability of the evidence with respect to two competing hypotheses, so that at least the researcher knows that evidence is more likely under one hypothesis than under a competing hypothesis. In addition, in the Bayesian scheme, it is possible to handle statistical hypotheses that are not specified precisely without resorting to a null hypothesis. For example, a researcher could test competing statistical hypotheses that the effect of the essay manipulation will be positive (experimental condition mean > control condition mean) or negative (experimental condition mean < control condition mean).

However, a disadvantage of Bayes is that one needs to know the prior probability distribution to compute Bayes Factors for continuous data. For a Bayesian, this is a subjective or arbitrary process, with different Bayesians suggesting different types of prior distributions (uniform, Cauchy, and so on). This disadvantage, arguably, is partially mitigated by the possibility of performing sensitivity analyses. Another disadvantage is that Bayes Factors are very sensitive to precisely how the competing statistical hypotheses are stated [12]. In addition to the foregoing example of a positive versus a negative statistical hypothesis, there could be positive versus zero, extremely positive versus mildly positive, extremely positive versus everything else, and so on. And within each of these general possibilities, there are varieties of ranges for both statistical hypotheses that can be specified. Seemingly small differences in how statistical hypotheses are specified may strongly influence the Bayes Factor that is obtained. More generally, then, Bayes Factors necessitate two largely arbitrary or subjective decisions. Which prior probability distribution should be used and how should competing statistical hypotheses be specified? Our argument is not that these are fatal for using Bayes, or even for using Bayes Factors.

Rather, it is that these arbitrary or subjective decisions are problematic for Bayes Factors being a valid measure of the strength of the evidence. The best one could say (and we will see later that even this does not work) is that Bayes Factors give the strength of the evidence with respect to:

a) One way of stating a statistical hypothesis,

b) Versus one way of stating a competing statistical hypothesis,

c) Under one way of specifying the prior probability distribution (though sensitivity analyses may help here). With respect to the strength of the evidence pertaining to empirical hypotheses, auxiliary assumptions, or theory, Bayes Factors lack much. And all becomes worse when basic criteria for valid measurement are considered.

The focus of this section is on the reliability and consequent validity of p-values. Subsections presented below concern attenuation of validity due to unreliability and the increase in statistical regression due to unreliability. There also will be a subsection showing that the reliability of p-values is low, thereby calling their validity, as a measure of the strength of the evidence pertaining to the statistical hypothesis, strongly into question.

It is a truism that measures should be valid and reliable. A measure is valid if it measures that which it is supposed to measure, but determining this is epistemologically complex, particularly as there is much debate about different ways to conceptualize validity, especially construct validity. Fortunately, such complexity is unnecessary at present. Everyone can agree that, whatever else matters for validity, minimum requirements are

a) The measure correlates with something (commonly termed as predictive or concurrent validity, depending on the time frame of the measures of the two variables) and

b) The measure is reliable. There is a classic theorem that relates validity, in the minimal correlative sense (concurrent or predictive), with reliability [13].

It is provided below as Equation 1 where is the observed correlation that can be expected between measures of two variables (observed validity), is the correlation between true scores of the measures of the two variables (true correlative validity, imagining perfect reliability), is the reliability of the measure of the variable designated as X, and is the reliability of the measure of the variable designated as Y:

Before continuing the main thread of the argument, it is important to consider two points with respect to the classical theory and Equation 1 [14,15]. First, a person’s “true score” on a measure is the expectation across a hypothetical set of many test-taking occasions. In this hypothetical scheme, the person takes the test, is mind-wiped to return to the same state as before taking the test, takes the test again, and so on, ad infinitum. Thus, a correlation between true scores is not the correlation between latent variables, across participants; but rather the correlation between expectations on two measures, across participants. It is not necessary to assume anything about latent variables. Thus, Lord and Novick [14] described the classical theory as “weak” in the sense of making minimal assumptions, relative to more powerful modern measurement theories such as generalizability theory and item response theory. However, an advantage of the weak assumptions of the classical theory is that they are subsumed by more modern measurement theories [1] and so any conclusion drawn from the classical theory also would be drawn from one of the more modern and powerful theories, whereas it is not necessarily the case that conclusions drawn from a more powerful theory would be drawn either from the classical theory or from another powerful theory.

Consequently, in those cases where the weak assumptions of the classical theory nevertheless suffice, an advantage is that there is no necessity to use stronger assumptions that are more likely to be wrong, misapplied, or not to fit with alternative measurement theories. Second, in the context of the classical theory, validity of a measure is correlative. An unavoidable consequence is that there is no way to obtain a pure validity coefficient of a measure as the correlation inevitably will depend on the reliability of the measure of concern, the reliability of the other measure, and the relationship between the two measures. However, it is possible to imagine that the other variable has perfect reliability, so that the product of the reliabilities of the two measures equals the reliability of the measure of concern. And it also is possible to assume various true validities and use Equation 1 to map out the consequences of unreliability of the measure of concern on the observed validity. Again, we emphasize that validity in this sense is correlative, and concerned with measures rather than with latent variables. Thus, it is a minimal type of validity that should not be confused with construct validity.

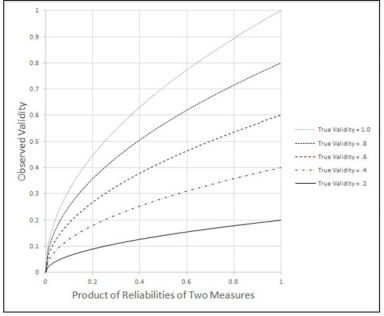
Equation 1 shows how the observed validity (in the correlative sense) attenuates from the true validity as the reliability of the measure decreases (if the reliability of the other variable is set at 1). As an extreme example, suppose that the measure has reliability = 0. In that case, the correlation one can expect to observe also will equal 0. Clearly, then, reliability sets an upper limit on validity. Although a reliable measure may or may not be valid, it is certain that an unreliable measure is not valid. In Figure 1, the product of the reliability of measures varies along the horizontal axis, from 0 to 1. In addition, the true correlation is set at .2, .4, .6, .8, and 1.00. Thus, the observed validity, along the vertical axis, is a function of the product of the reliability of the measures (or just the reliability of the measure if the reliability of the other measure is set at unity) and the true correlation. As one considers each curve in Figure 1, going from right to left, Figure 1 illustrates how unreliability attenuates observed validity. Because of this, substantive researchers usually set 8 or 7 as lower limits for “acceptable” reliability. We shall see later that p-value reliability is much less than 8 or 7.

Figure 1: Observed validity is expressed along the vertical axis as a function of the product of reliabilities of two measures along the horizontal axis and as a function of the true validity (five curves).

Many have pointed out that p-values have a sampling distribution, just like any other statistic [16,17]. A consequence of this fact is that p-values are subject to the phenomenon of statistical regression, sometimes termed regression to the mean. Because obtaining p-values less than .05 is tantamount to being a requirement for publication, the phenomenon of statistical regression renders replication problematic. Low p-values in original published research should be expected not to replicate, because of regression to larger p-values in replication attempts [16,17]. Obvious as the foregoing argument is, it nevertheless has not had much effect on statistical practice in the sciences. One reason might be that nobody has ever taken the trouble to calculate the extent of the effect, thereby rendering the argument too abstract to induce substantive researchers to change their scientific practices. The regression calculations are performed here using Equation 2-the standard formula describing statistical regression-where represents an individual score, the mean score of the population, and the reliability of the dependent variable at the population level:

To apply Equation 2 to p-values, it is necessary to consider the reliability of p-values. It is helpful to imagine a population of possible original studies, as well as a second population of replication studies, with p-values associated with each original study and with each replication study. In this ideal universe, where each replication study corresponds to an original study, it would be theoretically possible to obtain a correlation coefficient representing the strength of the relationship between p-values associated with the cohort of original studies and p-values associated with the cohort of replication studies. In short, we would have an estimate of the reliability coefficient of p-values (estimated ). In addition, in this ideal universe, there is no bias towards either high or low p-values, so the mean p-value is .5. If we substitute .5 into Equation 2, Equation 3 follows:

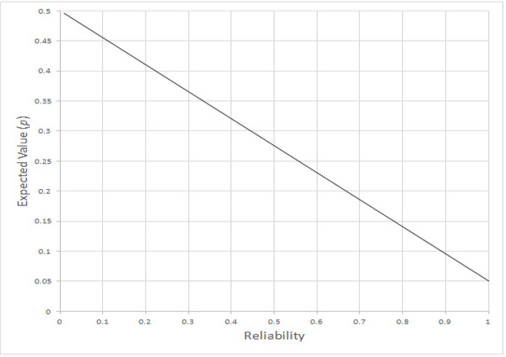
The main difficulty with applying Equation 3 to p-values is that it is unclear what the reliability of p-values happens to be. There are two obvious ways to address the difficulty. First, it is possible to let the reliability vary between 0 and 1 to determine the effect of statistical regression, in general. Second, we can make use of actual data, to be described later. To commence with a general demonstration, imagine that the p-value obtained in a study that has just been published is .05 (this is Z in Equation 3). The goal is to use Equation 3 to make the best prediction of the p-value that can be expected to be obtained in a replication study. Figure 2 illustrates how p-values much larger than .05 can be expected, upon replication, if the reliability of p-values is low, and that the problem is increasingly alleviated as the reliability of the p-values increases. However, even if we assume, unrealistically, that the p-value reliability is .9, statistical regression nevertheless implies that the best prediction for the p-value to be obtained in a replication study is .095 rather than the hoped for .05. We hasten to add that there is no implication that lower p-values are impossible in replication studies, only that the expected value is .095. And matters worsen very substantially as one moves from right to left in Figure 2. Thus, one would have to be an extreme optimist to assume that p-values in replication experiments would be likely to be close to original p-values.

Figure 2: The expected value for p in a replication study is represented along the vertical axis, based on having obtained p = .05 in the original study, as a function of the reliability of p-values along the horizontal axis.

The most systematic data that are available on the issue of replication can be obtained from the Open Science Collaboration Reproducibility Project. Researchers associated with this project replicated many studies published in top psychology journals, and anyone can download an EXCEL file from their website. From the present perspective, one complication is that although exact p-values were presented for the replication cohort of studies, inexact p-values were presented for the original cohort of studies (e.g., p < .05 rather than p = .023). Fortunately, the data file included test statistics (F, t, and so on) and degrees of freedom, so that EXCEL could provide exact p-values. With exact p-values having been obtained for both cohorts of studies, it only remained to have EXCEL provide the correlation between the two columns of p-values. The correlation is .004. This is consistent with the general tenor of their article in Science (Open Science Collaboration, [18], indicating skepticism about whether psychology is a replicable science. More to the present point, with reliability of .004, Equation 2 renders obvious that the regression value for an original p-value of .05 is close to whatever the mean p-value is [19,20].

In the idealized universe where there is no bias, and so the mean population p-value is .5, the regression p-value is extremely close to that (.4982). If we do not imagine an idealized universe, Equation 2 renders obvious that the regression p-value will be extremely close to the mean, and very little information is provided by the obtained p-value. And referring to Equation 1, the extremely low p-value reliability indicates that correlative validity is near zero, regardless of anything else. To be fair, the publication process induces factors that likely lowered p-value reliability, such as restriction of range, statistical regression, not having truly random samples, and others [21,22]. However, even making this concession, it seems unavoidable that at least as far as published p-values are concerned, reliability is low, whatever the reason. And if the reliability of p-values in published studies is low, as it clearly is, there is no reasonable way to support that they validly measure the strength of the evidence even with respect to null hypotheses. Possibly, the reliability of p-values would be raised if p-values played no role in the probability of acceptance of manuscripts for publication, as this would mitigate restriction of range as a problem [23].

But this solution, though it might improve the optics concerning the reliability of p-values, admits that p-values should not influence decisions of journal reviewers and editors. This would be quite an admission! Nor do matters improve if we consider Bayes Factors. If conditional probabilities fail, then quotients of conditional probabilities also fail. In fact, matters become even worse, as the unreliability of two conditional probabilities, rather than only one, becomes relevant. Given that attenuation due to unreliability and regression due to unreliability matter for a single conditional probability, they also matter for a quotient of two conditional probabilities [24-25].

In basic science, the goal is to propose and test theories. It is impossible to test theories without making auxiliary assumptions that connect non observational terms in theories with observational terms in empirical hypotheses. Consequently, the strength of the evidence depends strongly upon the worth of auxiliary assumptions, which is assessed by neither p-values nor Bayes Factors. A watered-down argument might be that p-values or Bayes Factors are at least good for assessing the strength of the evidence with respect to statistical hypotheses that admittedly are very far away from the theories they are used to test. But even this watereddown argument fails. This is because p-values are computed with respect to the null hypothesis, and not the researcher’s empirical hypothesis. Ubiquitously, the empirical hypothesis is inexact, and so it is impossible to form a point statistical hypothesis that can be tested with a p-value. Nor can the problem be solved with range hypotheses because this requires maximizing the p-value, which is an implicit admission that the computed value is not a precise measure of the strength of the evidence. Nor do Bayes Factors solve these issues.

To use Bayes Factors, the researcher must make arbitrary or subjective decisions about prior probability distributions, how to express one of the statistical hypotheses, and how to express the other of the statistical hypotheses. In addition to these considerations, a basic requirement of valid measures is that they must be reliable, but the foregoing section demonstrates that p-values and Bayes Factors fail there too. Conditional probabilities are unreliable, and consequently are strongly subject to attenuation due to unreliability and to regression due to unreliability-two ways of making the same point. Thus, if researchers are to continue to use p-values or Bayes Factors, they cannot justify that use by arguing that they are measuring the strength of the empirical evidence. Other justifications are needed.

1. Fisher RA (1925) Statistical methods for research workers. Edinburgh: Oliver and Boyd p. 66-70.
2. Fisher RA (1973) Statistical methods and scientific inference. Macmillan, London.
3. Lederman L (1993) The god particle: If the universe is the answer, what is the question? New York NYHoughton Mifflin Company 62: 191.
4. Popper KR (1959) The logic of scientific discovery. NY Basic Books, New York, USA.
5. Popper KR (1972) Objective knowledge. Oxford UK Oxford University Press.
6. Popper KR (1983) Realism and the aim of science. London Routledge, UK.
7. Lakatos I (1978) The methodology of scientific research programmes: Philosophical papers. Cambridge UK Cambridge University Press, UK.
8. Duhem P (1954) The aim and structure of physical theory. NY: Atheneum, New York, USA.
9. Trafimow D (2017) Why it is problematic to calculate probabilities of findings given range null hypotheses. Open Journal of Statistics 7: 483- 499.
10. Trafimow D, Earp BD (2017) Null hypothesis significance testing and Type I error: The domain problem. New Ideas in Psychology 45(1): 19- 27.
11. Trafimow D, Hughes JH (2012) Testing the death thought suppression and rebound hypothesis: Death thought accessibility following mortality salience decreases during a delay. Social Psychology and Personality Science 3(5): 622-629.
12. Chow SL (1996) Statistical significance: rationale, validity and utility. Sage Publications, London.
13. Greenwald AG (1975) Consequences of prejudice against the null hypothesis. Psychological Bulletin 82(1): 1-20.
14. Serlin RC,Lapsley DK (1985) Rationality in psychological research: The good-enough principle. American Psychologist 40(1): 73-83.
15. Serlin RC,Lapsley DK, G Keren,C Lewis (1993) Rational appraisal of psychological research and the good-enough principle. A Handbook for Data Analysis in the Behavioral Sciences: Methodological Issues pp. 199- 228.
16. Kass RE,Raftery AE (1995) Bayes factors. Journal of the American Statistical Association 90(430): 773-795.
17. Mayo D (1996) Error and the growth of experimental knowledge. Chicago The University of Chicago Press.
18. Spearman C (1904) The proof and measurement of association between two things. AmericanJournal of Psychology 15(1): 72-101.
19. Gulliksen H (1987) Theory of Mental Tests. Hillsdale NJLawrence Erlbaum Associates Publishers.
20. Halsey LG, Curran-Everett D, Vowler SL, Drummond GB (2015) The fickle P value generates irreproducible results. Nature Methods 12: 179-185.
21. (2015) Open Science Collaboration (2015) Estimating the reproducibility of psychological science. Science, 349(6251): 4716.
22. Cronbach LJ, Gleser GC, Nanda H, Rajaratnam N (1972) The dependability of behavioral measurements: Theory of generalizability for scores and profiles. John Wiley, New York, USA 178: 1275-1275A.
23. Hulin CL, Drasgow F, Parsons CK (1983) Item response theory: Application to psychological measurement.Homewood IL: Dow Jones- Irwin 26(3): 171-177.
24. Lederman L (1993) The god particle: If the universe is the answer, what is the question? New York NYHoughton Mifflin Company 62: 191.
25. Lord FM, Novick MR (1968) Statistical theories of mental test scores. Reading MA Addison-Wesley.