How Does Stathmin Destabilize Microtubules? A Root of Consciousness and Alzheimer’s Disease Volume 1 - Issue 5

Majid Monajjemi*¹, Farnoush Naghsh² and Afshar Alihosseini¹

• ¹Department of Chemical engineering, Central Tehran Branch, Islamic Azad University, Tehran, Iran
• ²Department of Chemistry, Science and Research Branch, Islamic Azad University, Tehran, Iran

Received: October 04, 2017;   Published: October 16, 2017

Corresponding author: Majid Monajjemi, Department of Chemical engineering, Central Tehran Branch, Islamic Azad University, Tehran, Iran

DOI: 10.26717/BJSTR.2017.01.000442

Abstract PDF

Alzheimer’s disease due to dementia and the memory brain that might be related to the microtubules disorder interrupt daily life. Alzheimer’s is a brain disease that causes a slow decline in concentrations, memory, thinking and reasoning skills. By this research we exhibited the important rules of stathmin destabilize microtubules as a root of this problem in view point of chemical molecular engineering.

Abbreviations: MT: Microyubule; SLD: Stathmin Like Domain; LOL: Localised Orbital Locator; ESP: Electro Static Potential; MAP: Microtubule Associated Proteins

Microtubule (MTs) is a long protein filament that forms of a dynamic cytoskeletal within a morphological change. MTs have multiple functions in the cellular processes including a peculiar biophysical setting in the internal environment. MTs grow and shrink continually in the living cells qua the harmony between these processes is vital for normal cell function [1-5]. Microtubules are tubularpolymers (as its name points) and its diameter is about 24 min which the hetero dimers are assembled head to tail in a polar fashion (This polarity is reflected by the distinction between the socalled plus and minus ends of proto-filaments). The “building brick” from which they are formed called alpha and beta-tubulins that are proteins and occurs in solution as a dimer of two similar subunits [4,5]. Their assembly is in part determined by the concentration of free tubulins in the cytoplasm [3].

Although most of MTs combinations are largely deprived from the cytoplasmic influence, 2 nm2 lateral pores and 200 nm² entrances at its ends are connected to cytoplasm [4, 5]. Recently, spherical particles have been found in the microtubules which the particles’ existence varied between cell types while the neuronal cells have the most particles [6-9]. In 1984, Burton exhibited the particles could be voided from the lumen quickly via reassembly or disassembly of intracellular microtubule [10]. Although identification of components inside of luminal has been difficult, during of the next 30 years observation of these particles in the microtubules lumen has culminated using vitreous cryo-electron microscopy [11].

These subunits polymerise end to end for formation protofilaments similar to a hollow tubes and their dynamic instability is controlled by numerous compounds. Proteins that destabilize microtubules have been identified recently (such as stathmin family proteins and Colchicine) [12-14]. These proteins increase microtubule turnover in cells, contributing to rapid reorganization of the microtubule cytoskeleton. Stathmin family was initially identified as a protein in response to extracellular signals, overexpressed in highly proliferative breast cancers and malignant ovarian cancers [15,16]. Stathmin is a cellular microtubule inhibitor, which forms a tight complex with two αβ-tubulin dimers, In the references [15,16] the structural information has shown how the stathmin protein family binds tubulin dimers and those studies suggest that phosphorylation occurs in a localized fashion, resulting in decreased microtubule destabilizing activity near microtubule polymer [17].

One of the important stathmin family proteins is RB3 which shares with other members the stathmin-like domain (SLD). Stathmin is a disordered protein, and their activities are downregulated by multiple phosphorylation. Stathmin is derived from the Greek word “stathmos” and it can also be translated as “terminal or stop”, which this translation loosely fits the microtubule destabilizing for the terminating or stopping microtubule growth [18]. Stathmin is a soluble, cytoplasmic protein which enforces an important function in regulating rapid microtubule remaking of the cytoskeleton in response to the cell’s requirements. At low concentrations of free tubulin in the cytoplasm, the growth rate at the microtubule ends is languid and results in an increased rate of disassembly (de-polymerization) [19]. The intracellular concentration of stathmin varies considerably among different cell types, ranging from0.005% up to 0.5% of the total cell protein [20], and in vertebrates, is expressed in cells with the potential to proliferate as well as in neurons [20,21].

Proteins related to stathmin are also expressed in the nervous system and include SCLIP, SCG10,RB3 (and two its splice variants RB3′& RB3′′) [21-23]. Non-polymerised tubulins exists as a hetero dimer of “α-tubulin” & “ β-tubulin” with binding sites for two molecules of guanosine triphosphate (GTP), one exchangeable and the other not. Via electron microscopy (EM) it can be seen that each proto-filament consists of globular 4nm subunits and it is possible for refined tubulin to assemble with a range of diameters containing between 9 and16 proto-filaments (Scheme 1). Only two atomic structures of αβ-tubulin are currently known which the first one is GDP-tubulin in straight anti parallel proto-filaments of twodimensional zinc sheets stabilized by Taxol (Figure 1) that has been employed to construct pseudo-atomic models of microtubules. The second is the curved structure of two head to tail GDP-tubulin dimers in complex with the stathmin-like domain of RB3 (RB3- SLD) [15-18].

Scheme 1 : The schematic images of various microtubules including “12-16” proto-filaments (pf).

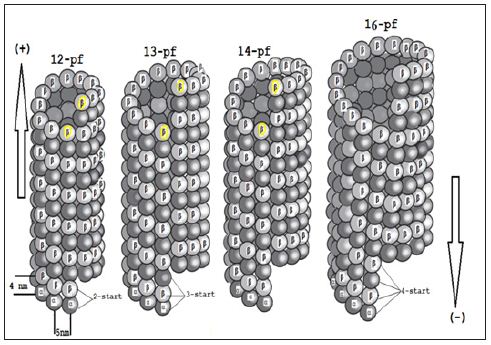
Figure 1 : Ribbon diagram of αβ-tubulin heterodimer.

The structure of tubulin in microtubules is related to the straight zinc-sheet structure, since both are made of similar proto-filaments, although the different lateral contacts cause modifications. Monomers in adjacent proto-filaments arrange a set of shallow helices, which for 13-protofilament microtubule 3 shallow helices run in parallel and for a smaller or larger number of proto-filaments there may be 2 or 4 shallo whelices. This difference provides some flexibility in the bonds between adjacent heterodimers (at least in the direction running around the microtubule). MT-associated motor proteins, such as dynein and kinesin can be run for long distances along a microtubule when there are 13 protofilaments (without switching lanes) [24,25]. In more or fewer than 13 proto-filaments, the structure must rotate somewhat, so that the proto-filaments twisted slowly around the microtubule axis [26].

The atomic structure of tubulin proto-filaments is discovered firstly from electron crystallography of zinc-induced 2D sheets [27]. Ravelli et al. [28] extracted important information about conformational change by X-ray crystallography. Each monomer has a pair of spherical domains set which the larger domain, containing the N-terminal half of the polypeptide, has the same fold as a “Rossmann fold” [29]. There is a binding site for the guanosine nucleotide on the plus end area of this domain that contact is made with the next subunit in the proto-filament. A binding site for “Taxol” is placed on the second domain of αβ-tubulin, whichalso makes contact with the core helix, on the opposite side from its contact with the nucleotide base (Figure 1). The C-terminal end of each tubulin polypeptide makes two long helices which those residues (from C-terminal) would be suitable for isoform recognition by tubulin binding proteins.

As it has exhibited in the (Figure 1), some long coil loops from the globular domains are complexed in lateral contacts between the proto-filaments in a microtubule. In addition there is common agreement that the “M-loops” of one proto-filament make contact with the guanosine triphosphate (GTPase) domains and the M-loops make different contacts with the adjacent proto-filament (Figure 1). In some positions the proto-filament forms a ring via bending at all of the interfaces between monomers. The bending of protofilament was first seen by electron microscopy [30] and has been confirmed in cocrystals of tubulin-sequestering protein stathmin by Gigant et al. [31]. The bending occurs even in the absence of destabilizing agents such as stathmin or colchicine. The core helix is a likely means of communication from the top to the bottom of the β-subunit via a cooperative mechanism. Whole microtubules can twist and bend without coming under great strain or snap and this is clear from images of fluorescently labelled microtubules growing [32].

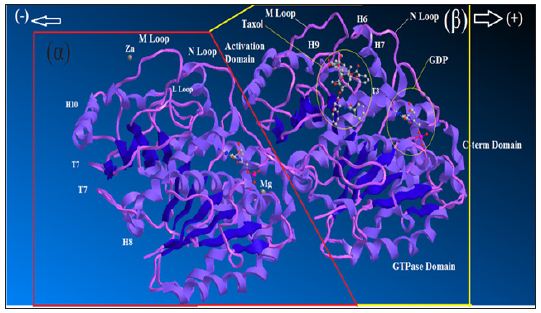
Although various stathmin activities have been reported, the mechanism by which stathmin affects microtubule dynamics is still a subject of argument. In this work theoretically, we found in vitro that the effects of stathmin can be concluded from its ability to form the strong bonded and non-bonded interaction via a ternary complex including α and β subunit tubulins, αβ hetero dimer of tubulins and one stathmin (Figure 2).

Figure 2 : Interaction of stathmin with 4 sub units of tubulin.

When a microtubule bends, individual proto-filaments are bent in a variety of directions. It is likely, therefore, that there are multiple “bent” states for dimers and proto-filaments and there is no certitude that the curved conformations induced by different agents of disassembly are identical. Many efforts have been made to characterize structurally the three major forms of microtubules, hetero dimers, and curved Proto-filament. The overall structure of the tubulin-stathmin complex has been suggested via scanning transmission electron microscopy combined with digital image processing [33,34].

Formation of the tubulins-stathmin complex introduced a new path to stabilize tubulin in solution for crystallization. Benoıt Gigant et al. [35] has been reported the 4 A˚ X-ray structure of a complex of GDP-tubulin with the “Escherichia coli”explicit stathmin-like domain of RB3 (RB3-SLD), a stathmin family protein. This shape defines the 3D structure of the complex, the arrangement of tubulins within this complex, and shows that RB3 contacts tubulin through a 91-residueα-helix. This structure helps to interpreter a clear model for tubulin -stathmin family combination in the nonbonded attraction and provides a structure of GDP-tubulin which is compared with the structure of tubulin in microtubules (Figure 1).

Ribbon diagram of αβ-tubulin heterodimer, the structure solved by electron crystallography using sheets of bovine brain tubulin in complex with Taxol [27] is shown in an orientation corresponding to the inside view of amicrotubule. The guanosine triphosphate “GTPase”domain, the activation domains, the core helix that connects the two globular domains in each monomer and the C-terminal domain on the external surface are shown.GTP is sandwiched between α and β tubulin subunits of each heterodimer. The nucleotide bound to β-tubulin has been hydrolyzed to GDP through contact with helix H8 and loop T7 of the activation domain of another α-tubulin subunit. Taxol sits in the pocket of β-tubulin on the inside face of microtubules. In -tubulin, this pocket is occupied by the extended L-loop [33].

Stathmin-Microtubules Interactions

Stathmin interacts with two molecules of dimeric α, β-tubulin to form a tight ternary complex which one mole of stathmin binds to two moles of tubulin dimers through the SLD [36]. Tubulin is able to switch between a curved structure in complex with the stathminlike domain of the RB3 protein and a straight microtubule-like structure. The proto-filament curvature and disassembly has done via GTP hydrolysis. The first opinion for GTP was thought that it would allosterically induce a straight conformation of tubulin subunits thorough-paced of microtubule assembly while the GDP would induce a curved conformation approving disassembly. Themicrotubule-associated proteins (MAPs) of tubulin-GDP protofilament spirals have indicated different intra- and inter-dimer curvatures [37]. However, this type of allosteric mechanism is challenged by the findings of curved structures of GTP-bound γ-tubulin [38].

This evidence led to a proposition that the free GTP-tubulin dimer is curved similarly to tubulin rings and is driven into the straight conformation by the microtubule (opposed to what was previously thought). So the GTP γ-phosphate only lowers the unfavorable free energy difference between the curved and the straight form [39]. Consequently, in the allosteric model GTP binding would induce a straighter conformation pre-structured in solution for lateral interactions [40] whereas in the lattice model [39] αβ- tubulin adopts a microtubule incompatible, curved conformation independent of the nucleotide state. It should me important to discuss of the GTP hydrolysis mechanism for destabilizing the microtubule lattice. To provide some answers to this question, Alushin et al. [41] exhibited a structural study for comparing highresolution cryo-EM reconstructions of GMPCPP microtubules and GDP microtubules. It shows that GTP hydrolysis induces a compression at the linear interface between dimers, immediately over the exchangeable nucleotide-binding site.

This compression is amalgamated by conformational changes in α-tubulin. In contrast, lateral contacts between α & β tubulins were basically unchanged in the different nucleotide states. These understanding suggest that GTP hydrolysis introduces strain into the lattice, but how this strain affects the strength of longitudinal and lateral bonds to destabilize the microtubule remains unknown. In this works 16 main sections have considered for investigation of bonded and non-bonded interaction between Stathmin with microtubules. Although the bonded situations and the GTP hydrolysis essentially are important for the proto-filament curvature and disassembly, the no bonded interaction helps to this processing in other side. More over this kind of non-bonded interaction provides the dynamic behavior for this phenomenon. It now seems clear that changes in the curvature of αβ-tubulin are fundamental to microtubule dynamics and the regulatory activities of microtubule-associated proteins (MAPs) during microtubule polymerization [42].

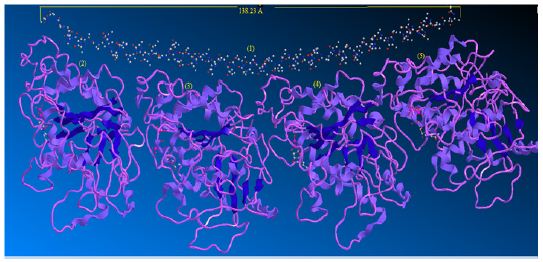
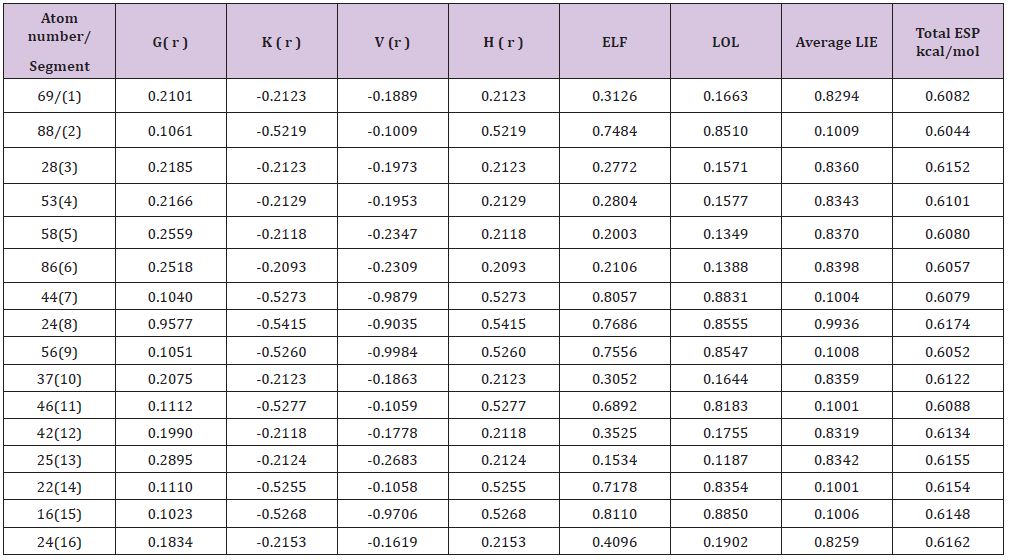
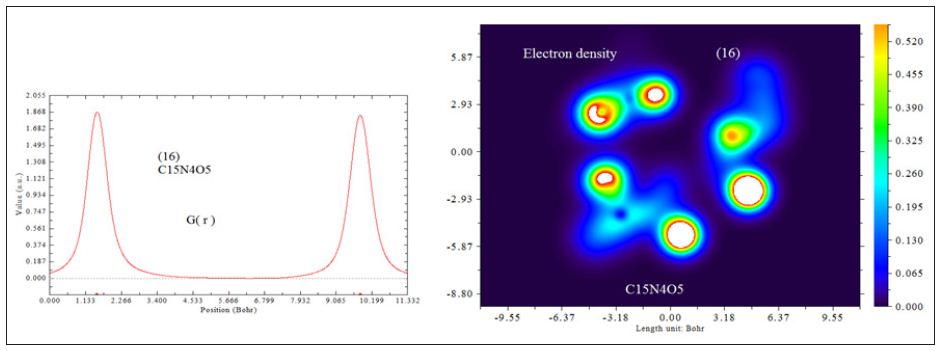
In this work it has been described a novel method of the stepfunction models for the microtubules within electron density profile in the composition of the stathmin. In this work we have focused on the electron density of the systems when each parts of 16 sections in stathmin has interaction one by one with α and β tubulin (Figures 1-3) (Tables 1 & 2). The electron density has been defined as

Figure 3 : 16 important section of stathmin.

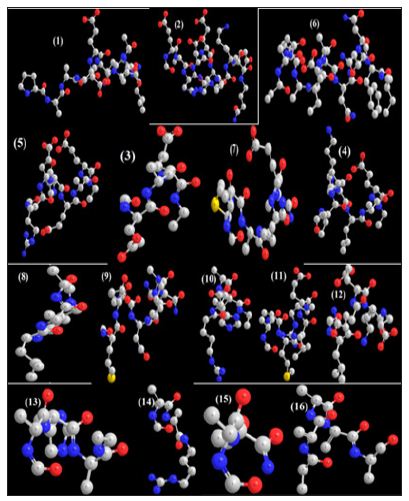
Table 1 : The Homo and Lumo of each system of 16 sections.

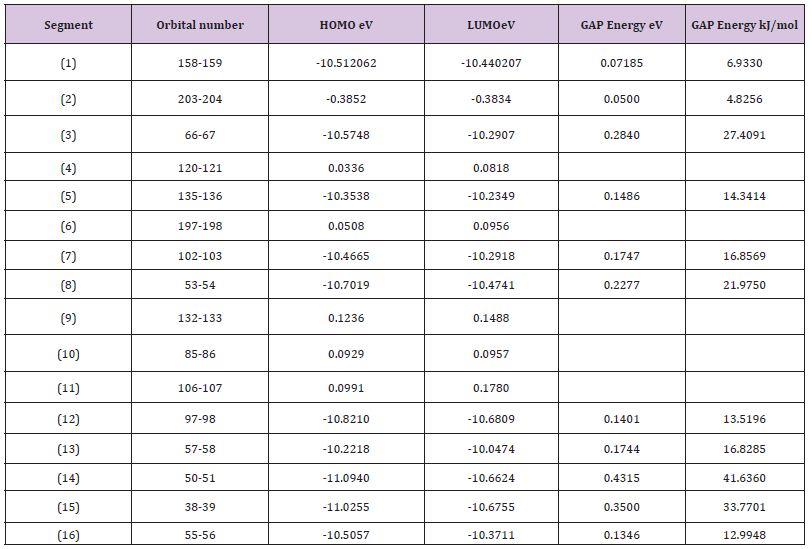
Table 2 : The various energies of each system of 16 sections.

Equation 1 :

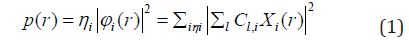
Where η_i is occupation number of orbital i, φ is orbital wave function, is basis function. C is coefficient matrix, the element of i_th row j_th column corresponds to the expansion coefficient of orbital j respect to basis function i. Atomic unit for electron density can be explicitly written as e/Bohr³. Baderm [43] found that the regions which have large electron localization must have large magnitudes of Fermi-hole integration. However, the Fermi hole is a six-dimension function and thus difficult to be studied visually. Becke and Edgecombe noted that spherically averaged like spin conditional pair probability has direct correlation with the Fermi hole and then suggested electron localization function (ELF) [44].

Equation 2 :

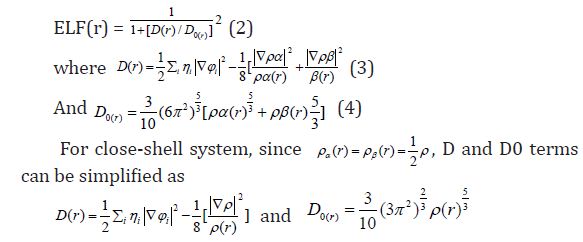
Savin et al. [45] have reinterpreted ELF in the view of kinetic energy, which makes ELF also meaningful for Kohn-Sham DFT wave-function or even post-HF wave-function. They indicated that D(r) reveals the by Pauli repulsion, while D0(r) can be considered as Thomas-Fermi kinetic energy density. Since D0(r) is introduced into ELF as reference, what the ELF reveals is actually a relative localization. ELF is within the range of (0,1).

A large ELF value means that electrons are greatly localized, indicating that there is a covalent bond, a lone pair or inner shells of the atom involved. ELF has been widely used for a wide variety of systems, such as organic and inorganic small molecules, atomic crystals, coordination compounds, clusters, and for different problems, such as the revealing atomic shell structure, classification of chemical bonding, verification of charge-shift bond, studying aromaticity. Notice that there is a deficiency of ELF, sometimes with r going beyond from molecular boundary, D(r) decreases faster than D0(r) and then ELF reaches 1 (completely localized). To overcome the problem, Multiwfn automatically adds a minimal value 10-5 to D(r). This treatment almost does not affect the ELF value in interesting regions [46]. In which the actual kinetic energy term in D(r) is replaced by Kirzhnits type second-order gradient expansion,that is

Equation 3 :

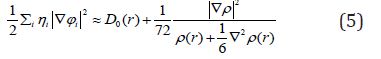
So that ELF is totally independent from wave-function, and then can be used to analyze electron density from X-ray diffraction data. Of course Tsirelson’s ELF can also be used to analyze electron density from quantum chemistry calculation, but is not as good as the ELF defined by Becke owing to the approximation introduced in kinetic energy term; however, qualitative conclusions can still be recovered in general. Localized orbital locator (LOL) is another function for locating high localization regions likewise ELF, defined by Schmider and Becke in the paper [47].

Equation 4 :

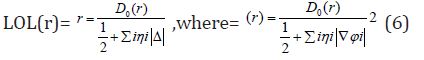
D₀ (r) For spin-polarized system and close-shell system are defined in the same way as in ELF. LOL has similar expression compared to ELF. Actually, the chemically significant regions that highlighted by LOL and ELF are generally qualitative comparable, while Jacobsen pointed out that LOL conveys more decisive and clearer picture than ELF, [48]. Obviously LOL can be interpreted in kinetic energy way as for ELF; however LOL can also be interpreted in view of localized orbital. Small (large) LOL value usually appears in boundary (inner) region of localized orbital’s because the gradient of orbital wave-function is large (small) in this area. The value range of LOL is identical to ELF, namely (0,1). The Total electrostatic potential (ESP) measures the electrostatic interaction between a unit point charges placed at r and the system of interest. A positive (negative) value implies that current position is dominated by nuclear (electronic) charges. Molecular electrostatic potential (ESP) has been widely used for prediction of nucleophilic and electrophilic sites for a long time. It is also valuable in studying hydrogen bonds, halogen bonds, molecular recognitions and the intermolecular interaction of aromatics. Moreover, based on statistical analysis, Murray and coworkers found a set of functions called GIPF [49-55], which connects ESP in molecular surface and macroscopic properties.

Computational details

We have simulated a part of microtubule systems including αβ -tubulin hetero dimer and stathmin through QM/MM simulation using Monte Carlo method. Each system was composed of 16 sections of stathmin molecules including interaction with tubulin [56]. Thermodynamic averages for molecular properties were determined from Monte Carlo methods, as can minimum-energystructures [57]. At finite temperature, clusters have finite vapor pressures, and particular cluster sizes are typically unstable to evaporation. Introducing a constraining potential enables one to define clusters of desired sizes. Composed of 16 sections of stathmin molecules were carried out with the simulation microtubules. The pressure was maintained by a variant of the extended system formalism, the Langevin Piston algorithm, which reduces oscillations in the cell parameters. The temperature was maintained at 300 K, well is the body temperature and identical to the relevant experiments.

Configurations of αβ -tubulin hetero dimer and stathmin consistent with a mean field were generated by Monte Carlo (MC) simulation, with field values adjusted to obtain agreement with experimental order parameters [58]. In this investigation, differences in force field are illustrated by comparing the calculated energy by using force fields AMBER and OPLS. Furthermore Hyper- Chem professional release 7.01 is used for the calculations. The final parameterization of stathmin was computed using self-consistent field calculations in order to find the optimal starting geometry, as well as the partial charges. We employed density functional theory with the van der Waals density functional to model the exchangecorrelation energies of αβ -tubulin hetero dimer. All optimization of 16 section of stathmin monomer were performed by Gauessian and GAMESS-US package [59]. We have mainly focused on getting the results from DFT methods such as m062x, m06-L, and m06 for the αβ -tubulin hetero dimer (Figures 4-9).

Figure 4 : 16 important section of stathmin.

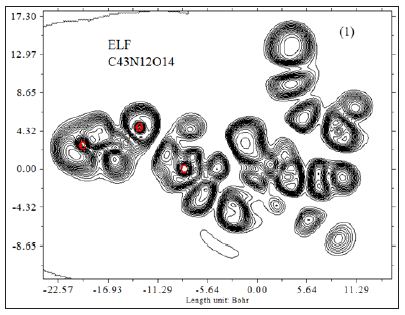
Figure 5 : 16 important section of stathmin.

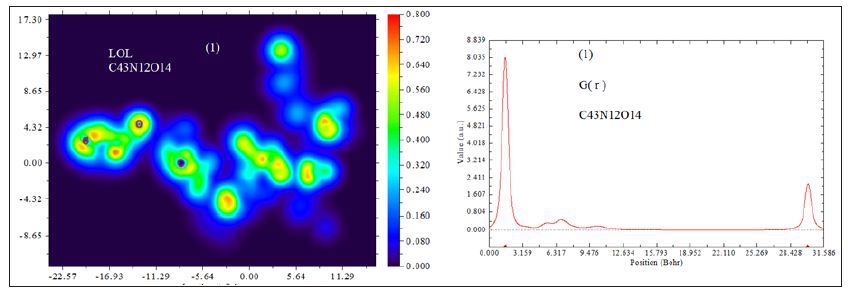
Figure 6 : 16 important section of stathmin.

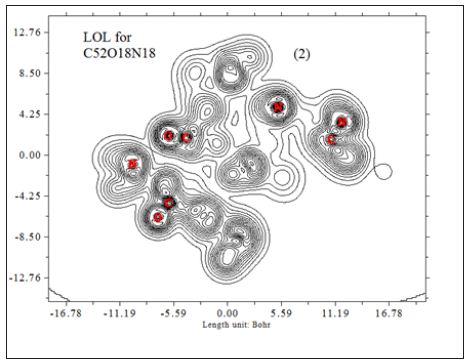
Figure 7 : 16 important section of stathmin.

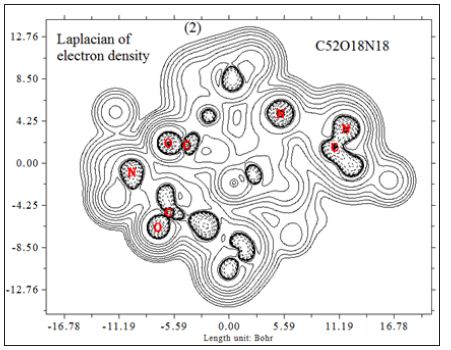
Figure 8 : 16 important section of stathmin.

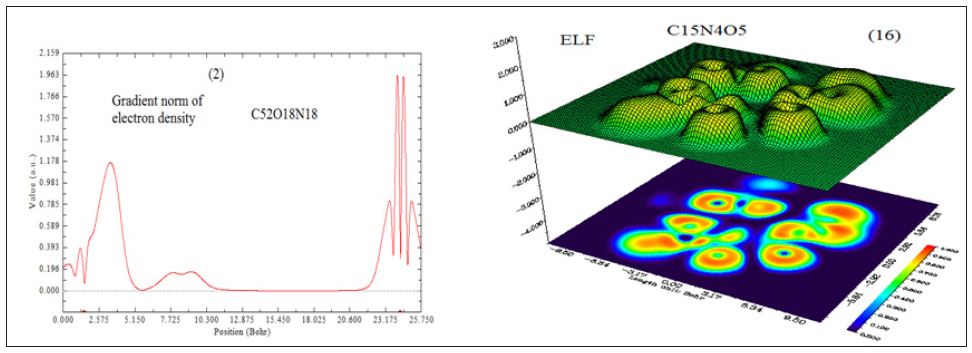
Figure 9 : 16 important section of stathmin.

The m062x, m06-L and m06-HF are rather new DFT functional with a good correspondence in non-bonded calculations between tubulin hetero dimer and are useful for the energies of distance between two fragments in phospholipids [60]. For non-covalent interactions, the B3LYP method is unable to describe van der Waals [61,62] microtubules systems by medium-range interactions such as the interactions of two tubulins. So the ONIOM methods including 3 levels of 1-high calculation (H), 2-medium calculation (M), and 3-low calculation (L) have been performed in our study for calculating the non-bonded interactions between tubulins. The ab-initio and DFT methods are used for the model system of the ONIOM layers and the semi empirical methods of Pm6 (including pseudo=lanl2) and Pm3MM are used for the medium and low layers, respectively. The semi empirical methods have been used in order to treat the non-bonded interactions between two tubulins.

B3LYP and the most other popular functional are insufficient to illustrate the exchange and correlation energy for distant non-bonded medium-range systems correctly. Moreover, some recent studies have shown that inaccuracy for the mediumrange exchange energies leads to large systematic errors in the prediction of molecular properties [63,64] Geometry optimizations and electronic structure calculations have been carried out using the m06 (DFT) functional. This approach is based on an iterative solution of the Kohn-Sham equation [65] of the density functional theory in a plane-wave set with the projector-augmented wave pseudo-potentials. The Perdew-Burke-Ernzerhof (PBE) [66] exchange-correlation (XC) functional of the generalized gradient approximation (GGA) is adopted. The optimizations of the lattice constants and the atomic coordinates are made by the minimization of the total energy.

The charge transfer and electrostatic potential-derived charge were also calculated using the Merz-Kollman-Singh [67], chelp [68], or chelp G [69]. The electron density (Both of Gradient norm & Laplacian), value of orbital wave-function, electron spin density, electrostatic potential from nuclear atomic charges, electron localization function (ELF), localized orbital locator (LOL defined by Becke & Tsirelson), total electrostatic potential (ESP), as well as the exchange-correlation density, correlation hole and correlation factor, and the average local ionization energy using the Multifunctional Wave-function Analyzer have also been calculatedin this study [70-73]. We used Multiwfn software to draw the contour line map [70,71]. The solid lines indicate positive regions, while the dash lines indicate negative regions.

We have plotted the contour line corresponding to vdW surface (electron density=0.001 a.u., which is defined by R. F. W Bader). This is useful to analyze distribution of electrostatic potential on vdW surface. Such a contour line has also been plotted in gradient line and vector field map by the same option. Color, label size and line style of the contour line can be changed based on models. The relief map was used to present the height value at every point. If the values are too large, they will be truncated in the graph. Therefore, it can be chosen to scale the data with a factor to avoid truncation. The graph is shown on interactive interface. Shaded surface map and shaded surface map with projection are used in our representation of height value at each situation [70-73].

By this work it has been exhibited the mechanism of microtubules are related to tubulins interaction with stathmin. Each section of 16 parts of stathmin has specific rules for nonbonded interaction between tubulins and stathmin. These subunits polymerise end to end for formation proto -filaments similar to a hollow tubes and their dynamic instability is controlled by numerous compounds. The bending occurs even in the absence of de-stabilizing agents such as stathmin or colchicine. The core helix is a likely means of communication from the top to the bottom of the β-subunit via a cooperative mechanism.

1. Charak Sanhita Part I (1975) Jaynendra Press New Delhi, India 27: 249.
2. Meyer, LH (1960) Food chemistry. Litton Educational Publishing, Inc. USA.
3. Sharma R, Khan S (2007) Health aspects of traditionally processed indigenous edible oils. Recent Progress in Medicinal Plants, Natural Products-II stadium, Press LLC, USA 18: 430.
4. Sharma R, R Bhutra, S Acharya, MRK Sherwani (2007) Comparative analysis of four edible oils for stability against longer storage and heat deterioration during frying. J lipid sci and Technology 39: 3.
5. Hildich TP, PN William (1964) Chemical Constitution of Natural Fats. 4th edn. Chapman & Hall, London.
6. Tewfilk IH, HM Ismail, S Sumar (1998) The effect of Intermittent heating on some chemical parameters of refined oils used in Egypt. A Public health nutrition concern. Int J Food Sci Nutr 49(5): 339-342.
7. Goburdun D, B Jhuree (1995) Effect of deep fat frying on fat oxidation in soyabean oil. Int J Food Sci Nutr 46(4): 363-371.
8. Esterbauer H (1993) Cytotoxicity and genotoxicity of lipid-oxidation products. Am J of Clinical Nutrition 57(5): 779S-785S.
9. Woodside JV, IS Young (2001) Dietary antioxidants and protection from coronary heart diseases. In: Nutritional Health: Strategies for disease prevention. Eds: Wilson T and Temple NI Humana Press, Totowa, USA.
10. Byers T (1997) Hardened fats, hardened arteries? New England. Journal of Medicine 337: 1543-1545.
11. Ascherio A, Katan MB, Stampfer MJ, Peter L Zock, Walter C Willett (1999) Trans fatty acids and coronary heart diseases. New England Journal of Medicine 340: 1994-1998.
12. Law M (2000) Plant sterol and stanol margarines and health. BMJ 320(7238): 861-864.
13. Tyagi VK, Vashishtha AK (1994) Effect of deep fat frying on the characteristics and composition of soyabean oil. J Oil Technologist’s Association of India 26: 111.
14. Tyagi VK, Pramod Kumar (1995) Formation of polymeric fractions in frying fats. J Oil Technologist’s Association of India 26: 363.
15. Shiva V (2000) Stolen Harvest: The Hijacking of the Global Food Supply. South End Press, Cambridge, MA.
16. RangaSwamy Baby Latha, Prabhdial Singh, Nasirullah (2008) J Lipid Sci and Technology 40(2): 59-64.
17. Nasirullah, Rangaswamy Baby latha (2009) J Lipid Sci and Technology 41(1): 10-14.
18. Yale J Biol Pred, Sankar D et al. (2006) Department of Bio Technology, Vinayaka Mission Research Foundation University, Paiyanoor chennai, India.
19. (2005) J Nutr Sci. Vitaminol, Tokyo 51(4): 223-230.
20. (2005 ) J Med. Food Fall 18(3): 377-381.
21. (2005) Alcohol Clin. Exp. Res 29(11): 116S-120S.
22. Peanuts : Worlds Healthiest foods, Wh foods Com.
23. Sanders TH, Mc Micheal RW, Hendrix KW (2000) “Occurance of resveratrol in edible peanuts “Journal of agriculture and food chemistry 48(4): 1243-1246.
24. (2007) “Coenzyme Q 10 “ American Cancer Society.
25. (2003) Clinical Versatility of Antioxidants and w-6/w-3 PUFA content in Edible Vegetable Oil- Shyam Prakash et al. National Convention on Health, Nutrition and value Addition, New Delhi, p. 22.
26. (2005) Food and Nutrition, Priya Bhargava, Tarachand, Commen Wealth Publishers, pp. 209- 2.