Research ArticleOpen Access

The Distinguishing Role of 2.f(O) – f(H) in Electrolytic Systems

Volume 8 - Issue 1

Anna Maria Michałowska Kaczmarczyk¹ and Tadeusz Michałowski²*

Author Information Open or Close
- ¹Department of Oncology, The University Hospital in Cracow, Poland
- ²Department of Analytical Chemistry, Technical University of Cracow, Poland
*Corresponding author: Tadeusz Michałowski, Department of Analytical Chemistry, Technical University of Cracow, Cracow, Poland

Received: July 18, 2018; Published: August 16, 2018

DOI: 10.26717/BJSTR.2018.08.001591

Full Text PDF

To view the Full Article Peer-reviewed Article PDF

Abstract

The linear combination f₁₂ = 2⋅f(O) – f(H) of elemental balances: f₁ = f(H) for H and f₂ = f(O) for O is the keystone in formulation of Generalized Electron Balance (GEB), which completes the set of equations necessary for resolution of an electrolytic redox system according to Approach II to GEB in aqueous media. The f₁₂ does not involve the numbers of free and hydrating water molecules. The linear dependency or independency of f₁₂ from charge balance (f₀ = ChB) and other elemental/core balances f_k = f(Y_k) (k=3…,K) for elements/cores Y_k of the system is the general criterion distinguishing between non-redox and redox systems. This criterion is provided by linear combination 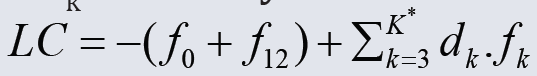, where K* (≤K) is the number of electron-non-active elements (fans) of the system, and dk are the multipliers related to oxidation numbers (ONs) of the elements involved in Yk. For non-redox systems, LC is transformed into identity, 0 = 0, whereas for redox systems, the LC and each linear combination , where a_k ∈ ℝ, are different from identity. The ONs, reductant, oxidant are derivative concepts in this formulation. All these interesting regularities are illustrated by simulated titration in a symproportionating redox system, resolved according to Generalized Approach to Electrolytic Systems (GATES) principles.