info@biomedres.us
+1 (502) 904-2126
One Westbrook Corporate Center, Suite 300, Westchester, IL 60154, USA
Site Map
ISSN: 2574 -1241
ISSN: 2574 -1241
Received: July 18,2018; Published: August 16,2018
*Corresponding author: Tadeusz Micha∤owski, Department of Analytical Chemistry, Technical University of Cracow, Cracow, Poland
DOI: 10.26717/BJSTR.2018.08.001591
The linear combination f12 = 2 f(O) - f(H) of elemental balances: f1 = f(H) for H and f2 = f(O) for O is the keystone in formulation of Generalized Electron Balance (GEB), which completes the set of equations necessary for resolution of an electrolytic redox system according to Approach II to GEB in aqueous media. The f does not involve the numbers of free and hydrating water molecules. The linear dependency or independency of f12 from charge balance (f0 = ChB) and other elemental/core balances fk = f(Yk) (k=3...,K) for elements/cores Yk of the system is the general criterion distinguishing between non-redox and redox systems. This criterion is provided by linear combination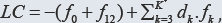 
where K* (≤K) is the number of electron-non-active elements (fans) of the system, and dk are the multipliers related to oxidation numbers (ONs) of the elements involved in Yk. For non-redox systems, LC is transformed into identity, 0 = 0, whereas for redox systems, the LC and each linear combination 
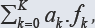are different from identity. The ONs, reductant, oxidant are derivative concepts in this formulation. All these interesting regularities are illustrated by simulated titration in a symproportionating redox system, resolved according to Generalized Approach to Electrolytic Systems (GATES) principles.
The Generalized Electron Balance (GEB) [1-6] concept, related to electrolytic redox systems, is put in context with the principle of conservation of all elements in electrolytic redox systems, in aqueous, non-aqueous or mixed-solvent media. Two equivalent approaches to GEB, termed as the Approaches I and II to GEB, were formulated. The Approach I, when perceived in convention of card game, is based on the common pool of electrons as money, introduced by electron-active elements, named as players; elec- tron-non-active elements are called there as fans [3]. The GEB, formulated according to Approach II, results from the linear combination f12 = 2-f(O) - f(H) of elemental balances: f1 = f(H) for H, and f2 = f(O) for O. For a redox system, the f is linearly independent on charge balance (f0 = ChB) and other elemental balances fk = f(Yk) (Yk ≠ H, O; k=3...,K); all the balances are presented here as equations, fk = 0. For a non-redox system, f is linearly dependent on f0,f3...,fK. The redox system is described with use of K independent balances f0,f12,f3...,fK, whereas a non-redox system is described with use of K-1 independent balances f0,f3...,fK. This property of f12 provides the general criterion distinguishing between redox and non-redox systems of any degree of complexity, namely: equilibrium, non-equilibrium and metastable, mono- and polyphase, static and dynamic electrolytic systems, also in mixed-solvent media. The GEB enters, as GATES/GEB, the Generalized Approach to Electrolytic Systems (GATES), i.e. GATES/GEB ⊂ GATES.
The linear combination 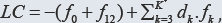(1) is formulated, where all fans (K* elements) of the system are involved; K* = K for a non-redox system, K* < K for a redox system, where K-K* players are involved. When dk are equal to the oxidation numbers (ONs) of elements in the corresponding fans (k=1...,K) of a non-redox system, then LC is transformed into identity, 0 = 0. For a redox system, LC assumes the simpler form, where only the species and components related to players are involved. The f12 is considered as the primary form of GEB, f12 = pr-GEB. The f12, LC (Eq. 1) and any other combination 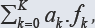have full properties of GEB, although - for obvious reasons - the simplest/shortest form of GEB, involving the smallest number of components, is more desirable. The GEB concept is perceived as the law of the matter conservation, as the general law of Nature, as the hidden connection of physicochemical laws, and as a breakthrough in thermodynamic theory of electrolytic redox systems [3,7-15]. The GATES/GEB is perceived as an example of excellent paradigm, as the best possible thermodynamic approach to electrolytic redox systems [16].
We refer here to a dynamic D+T system (aqueous medium), composed of titrand D and titrant T; V mL of T is added into V0 mL of D according to titrimetric mode, and V0+V mL of D+T mixture is obtained at a given point of the titration T(V) D(V0), if the assumption of the volumes additivity is valid/tolerable. In this system, the species Xi(zi)> exist as hydrates Xi(zi) ; zi = 0, ±1, ±2,...is a charge, expressed in terms of elementary charge units, e = F/NA (F = 96485 C-mol-1 - Faraday's constant, NA = 6.022-1023 mol-1 - Avogadro's number, ni =niw ≥ 0 is a mean number of water (W=H2O) molecules attached to ; the case niW=0 is then also admitted. For ordering purposes, we assume:Xz22 ni2W = H+1-n2W, Xz33 n3W = OH- 1-n3W, i.e., z2 = +1, z3 = -1, ... . The n, = niW values are virtually unknown - even for xz22 = H+1 [17] in aqueous media and depend on ionic strength (I) of the solution.
It is advisable to start the balancing from the interrelations between numbers of particular entities: N0j for components repre-sented by molecules composing D and T, and Ni - for species (ions and molecules) of i-th kind (i = 1...,I), where I is the number of kinds of the species xzii niW in D+T. The N0j (j=1,2...,J) is the number of molecules of the component of j-th kind, including water, forming D in static (V=0), or D and T in a dynamic D+T system. The mono- or two-phase electrolytic D+T system thus obtained involve N1 molecules of H2O (xzi1 = H2O(z= 0) and Ni species of i-th kind, xzii niw (i=2, 3,...,I), specified briefly as xzi i(Nini), wheren ≡i niw ≡niH2O is the mean number of hydrating water molecules (W=H2O) attached toxzii niw The net charge of xzii niw equals to the charge of xiz, zi +niW 0 = z. For ordering purposes, we write the sequence: H+1 (N2, n2), OH-1 (N3, n3), .... Molar concentration of the species xzii niwis denoted as[xzii]. For a dynamic D+T system we have [xzii]= 103-(N./Na)/(V0+V) (2)
‘Electrolytic (redox and non-redox) systems are formulated according to the GATES principles [1], and the set of K+1 balances f0, f1, f2, f3..., fK is thus obtained. The charged/ionic species X,o -nW of the system are involved in the charge balance (ChB)
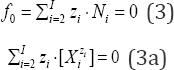
applicable for static and dynamic systems. Note that 0- [Xm]= 0 for a species Xm. nmw with zero charge (zm=0), e.g., 0^ [H2O] = 0 (z1=0).
Free water particles (N1), and water bound in the hydrates
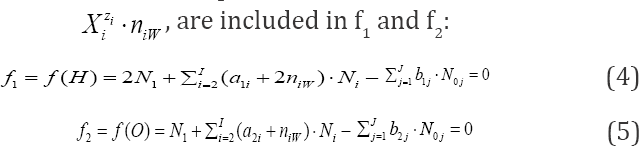
Next, the linear combination
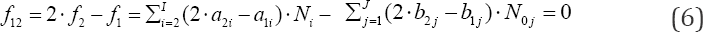
is obtained, where aki and bkj in equations (4)-(6) are the numbers of atoms/cores y(k=1 k(k=1.....k)in xzii niw and in the j-th component of the system, resp. A core is perceived as non-transformable cluster of atoms, of the same elemental composition (expressed by chemical formula) and structure; the cores are involved only with fans. One can notice that: (a) N1 involved with H2O as the species, (b) all N0i related to water as the component of the system, and (c) all ni = niW specified in f(H) and f(O), are cancelled within 2-f(O) - f(H) in aqueous media. The necessity of prior knowledge of niW values in the balancing procedure is thus avoided. All these regularities are valid for non-redox and redox systems. The elemental/core balances: f3..., fK, interrelating the numbers of atoms/cores Yk * H, O in components and species, are as follows
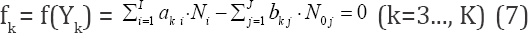
In an electrolytic system, with K elements/cores involved in it, where H and O do not participate as players, we arrange the elemental/core balances in the sequence f1, f2...,,,...,fK , where K* is the number of fans. Then we formulate the linear combination
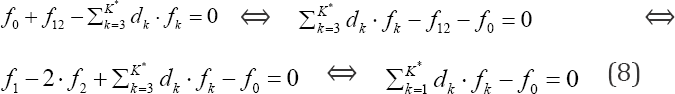
involving balances: f0, f12, f3., fk* for all fans. In particular, d1 = +1, d2 = -2.
In a non-redox system, we have K* = K fans, i.e., the number of players equals zero, K -K*= 0. In a redox system, we have K* fans, K* < K, i.e., the number of players equals K - K* (> 0). When the multipliers dk are equal to (or involved with) the oxidation num-bers (ONs) of the corresponding elements (k=1..., K) in fans of a non-redox system, then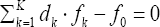 
(Eq. 8) is transformed into identity, 0 = 0. This proves that f12 is not the independent equation in the set 
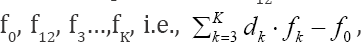and then fo, f3....fK is the
set of K-1 independent balances, composed of charge balance (f0) and K-2 elemental/core balances f3,.,fK. Referring now to a redox system, we state that the Eq. (8), i.e.,
involving the balances for all K* fans, with dk (k=1..., K*) equal to ONs of elements in fans, gives the balance involving only the com-ponents (N., N0j) related to players in species and compounds, with coefficients equal to (or involved with) ONs of these elements. To facilitate the purposeful linear combination of the balances that enables to avoid possible/simple mistakes in the realization of the linear combination procedure, we apply the equivalent relations:
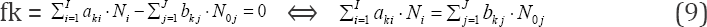
for elements with negative oxidation numbers, or
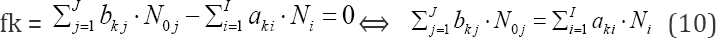
for elements with positive oxidation numbers, k 6 3., K; the change of places of numbers Ni for components and N0j for species around equality sign is realized here.
We consider the T(V) D(V0) titration, where V mL of C mol/L KIO3 is added into V0 mL of KI (C0) + HCl (C01); V mL of T is composed of N molecules of KIO3 and N02 molecules of H2O, and V0 mL of D is composed of N03 molecules of KI, N04 molecules of HCl and N05 molecules of H2O. In the D+T system thus formed we have the following species:
H2O (N1), H+1 (N2, n2), OH-1 (N3, n3), K+1 (N4 n4), I-1 (N5, n5), I3-1 (N6 n6) I2 (N7 n7), I2(s) (N8 n8), HI0(N9 n9), IO-1 (N10, n10), HIO3 (N11 n11), IO3-1 (N12, n12), H5IO6 (N13, n13), H4IO6-1 (N14, n14), H3IO6-2 (N15, n15, Cl-1 (N16, n16), Cl2 (N17, n17), HClO (N18, n18), ClO-1 (N19, n19,), HClO2 (N20, n20), ClO-12 (N21, n21), ClO2 (N22, n22), ClO-13 (N23, n23), ClO4-1 (N24,n24) I2Cl-1 (N25,n25)ICl (N26,n26) ICl2-1 (N27,n27) (11)
where I2(s)is the solid (s) iodine, characterized by solubility s =1.3310-3 mol/L in aqueous media (25 oC).
For the system specified above, we formulate the charge (f0) and elemental (f1, f2, f3, f4, f5) balances:
The set of balances presented above was formulated according to Approach II to GEB, for the redox system with K - 5 elements: H, O, K, I, Cl involved. In accordance with the terminology applied in [3], we have their K* = 3 fans: H, O, K, and K - K* = 5 - 3 = 2 players: I and Cl. The balance f12 = 2-f(O) - f(H) (Eq. 18a) involves also the species: H+1, OH-1 composed only of fans (H, O). These species are cancelled in the linear combination f12 + f0. On the other hand, the species formed by players and fans, where H and O are not involved, i.e., K+1, I-1, I3-1, I 2, I 2(s), Cl-1, Cl2 , I2Cl-1, ICl and ICl -1, are also cancelled within f. The linear combination f + f0 - f3 = 0 (Eq. 19) composed of f0 and balances for fans: f1, f2, f3 includes only the species where players are involved. Note that the coefficients/multipliers for the balances: f1, f2, f3 are equal to ONs for the elements: H, O and K, respectively. The coefficients at concentrations in Eq. (22) are equal to the products of numbers of the player's atoms and the related ONs, see e.g., (-1).[I-1] = ≡1-(-1)-[I-1], 3-(-+)-[I3-1], 0-[I2] = 2 0-[I2], and 0-[I2(s)] = 2-0-[I2(s)]). In I2Cl-1, ICl and ICl2-1, where only players (I, Cl) are involved (Eq. 22), the coefficients are weighed sums of ONs of the players.
As results from the above, the formulation made according to Approach II to GEB does not require prior knowledge of oxidation numbers for all elements (players, fans) of the system in question. The roles of oxidants and reductants are not ascribed to components and species. Within the Approach II to GEB, the terms: oxidation number (ON), oxidant and reductant are derivative concepts.
In the D+T system considered above, calculation of ONs for all the elements is an easy task, however. Therefore, one can use here Approach I to GEB, known also as the 'short version’ of GEB [3]. In the Approach I to GEB, the players, and their ONs in the components and species are indicated.
Unlike the Approach II exemplified above, the Approach I to GEB needs prior knowledge of ONs for all (K = 5) elements in com-ponents and species of the system in question. In the D+T system, there are K* = 3 'fans', whereas iodine (I) and chlorine (Cl) are considered as players; KI and KIO3 are the carriers of iodine electrons, whereas HCl is the carrier of chlorine electrons. One molecule of KIO3 involves ZI-5 iodine electrons, one molecule of KI involves ZI+1 iodine electron, and one molecule of HCl involves ZCl+1 iodine electron. Then N molecules of KIO3 involve (ZI-5) N iodine electrons, N03 molecules of KI involve (ZI+1) -N03 iodine electrons, and N04 molecules of HCl involve (ZCl+1) -N04 chlorine electrons. Thus, the total number of the players' electrons introduced by the solutes in this system is (ZI-5) N01 + (ZI+1) N03 + (ZCl+1) N04. Referring to the species where the players are involved, we state that:
a) N5 species I-1-n5H2O involve (Z1+1) -Ns iodine electrons;
b) N6 species I3-1-n6H2O involve (3Z1+1) -N6 iodine electrons;
c) N7 species I2-n7H2O involve 2Z1N7 iodine electrons;
d) N8 species I2(s.n8H2O involve 2Z1N8 iodine electrons;
e) N9 species HIO-n9H2O involve (Z1-1) N iodine electrons;
f) N species IO-1n10H2O involve (Z1-1) W iodin electrons;
g) N11pecies HIO3.n11H2O involve (Z1-5) -N iodine electrons;
h) N12 species IO3-1.n12H2O involve (Z:-5) W iodine electrons;
i) N13 species H5IO6n13H2O involve (Z:-7) .N13 iodine electrons;
j) N14 species H4IO6-1.n14H2O involve (Z1-7) .N14 iodine electrons;
k) N15 species H3IO6-2.n15H2O involve (Z1-7) .N1S iodine electrons;
l) N16 species Cl-1-n H2O involve (ZCl+1) W chlorine electrons;
m) N17 species Cl2-n17H2O involve 2ZCl.N chlorine electrons;
n) N species HClO.n18H2O involve (ZCl-1) W chlorine electrons;
o) N19 species ClO-1.n19H2O involve (ZCl-1) .N19 chlorine electrons;
p) N20 species HClO2-n20H2O involve (ZCl-1) .N20 chlorine electrons;
q) N21 species ClO2-1.n21H2O involve (ZCl-1) .N21 chlorine electrons;
r) N22 species ClO2.n22H2O involve (ZCl-1) -N22 chlorine electrons;
s) N23 species ClO3-1-n23H2O involve (ZCl-1) W chlorine electrons;
t) N24 species ClO4-1.n24H2O involve (ZCl-1) W chlorine electrons;
u) N25 species I2Cl-1.n25H2O involve (2Zj+ZCl+1) .N25 io- dine+chlorine electrons;
v) N26 species ICl.n26H2O involve (Z,+ZCl) .N26 iodine+chlorine electrons;
w) N27 species ICl2-1.n27H2O involve (Zj+2ZCl+1) .N27 io- dine+chlorine electrons.
Approach II to GEB ↔ Approach I to GEB (24)
For more details - see [3] (pp. 41-43).
We can also formulate the balances for D and T, considered separately, as independent units. Applying the notation specified above, we have:
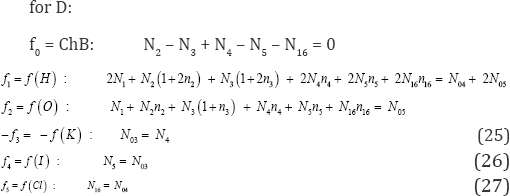
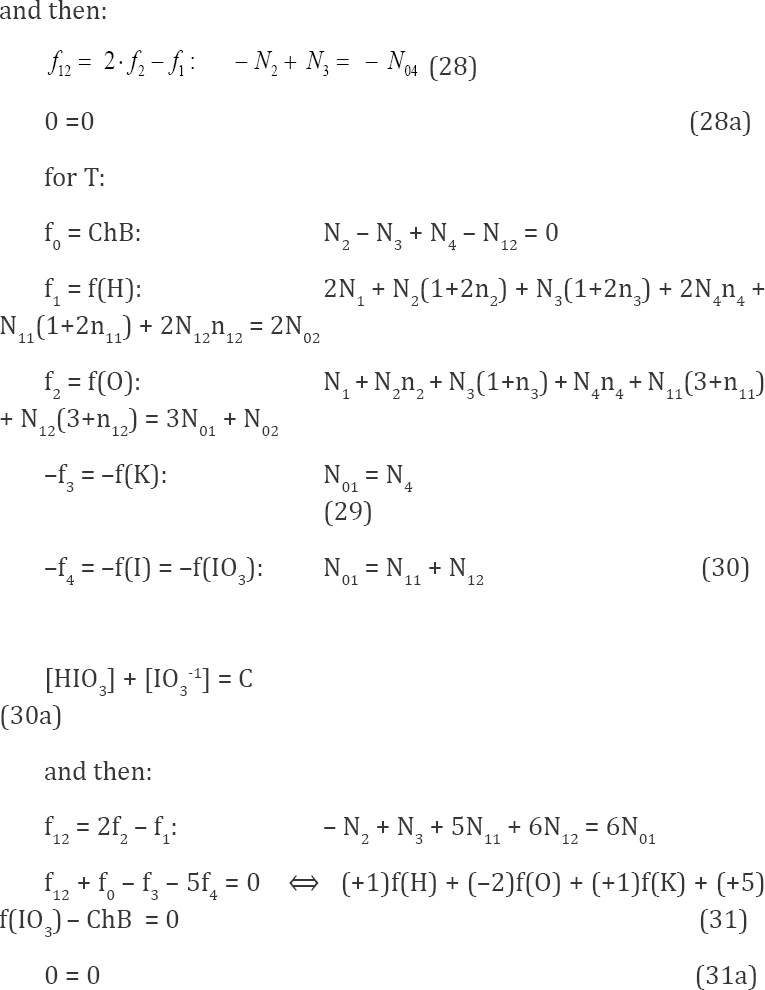
The relations 0 = 0, see (28a) and (31a), named as identities,mean here that:
a) f12 is linearly dependent on: f0, f3, f4 and f5 in Eq. (28), i.e., f12 = f3 - f4 - f5 - f0;?
b) f12 is linearly dependent on: f0, f3 and f4 in Eq. (31), i.e., f12 = f3 + 5f4 -f0.
In other words, the f12 are not the independent equations in D and T, considered here as separate subsystems.
It can be added that IO3-1 can be considered in T as the core, see Eq. (30a); IO3-1 is not considered as the core in the D+T system, considered in section 3.
The computer program is analogous /like one presented elsewhere [14,18-20]. The values for parameters of the system were as follows: V0 = 10; C0 = 0.01; C01 = 0, 0.2 or 5.0; C = 0.1. The independent variables: x (1) - E, x(2) - pH, x(3) - pI, x(4) - pCl were applied for the set of equations: (23a) for GEB, (12a) for ChB, (16a) for iodide, (17a) for chloride, rewritten as follows:
As we see, the number of balances (equations 23b, 12b, 16b, 17b) related to the system in question is equal to the number of independent variables: x(1), x(2), x(3), x(4) (i.e., 4 = 4). The relation (15a) is considered as equality, not equation; at pre-assumed C0, C and V0 values, it is simply a number (not variable!) at given V value; V is considered as parameter (not variable!) at defined step of calculation procedure, realized according to iterative computer program, e.g. MATLAB [1].
Some representative curves are plotted in Figures 1 - 5, as functions of the fraction titrated Φ [21] on the abscissa
The curve s in Figures 1a-1c are related to absence of HCl (C01 = 0) in D. The main products of the symproportio-nation reaction, indicated in Figure 1a, are formed in reactions:
Figure 1: The plots for (1a) speciation curves, and (b) pH = pH(Φ), (1c) E = E(Φ) relationships, at C01 = 0 and (C0, C, V0) = (0.01, 0.1, 10).
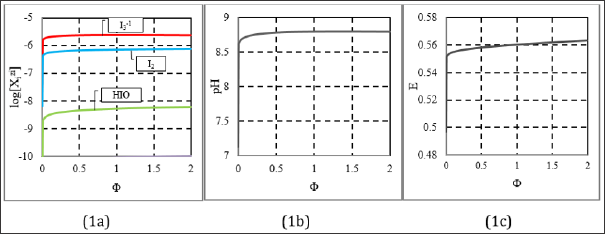
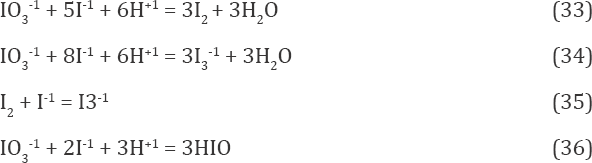
only with very slight efficiencies, ca. 10-6 mol/L for I3-1. The (weakly) alkaline reaction of the mixture (Fig. 1b) is expected based on simplified form of ChB
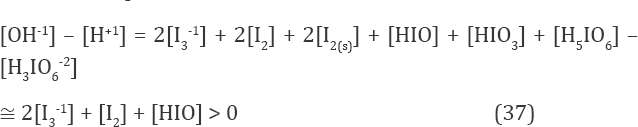
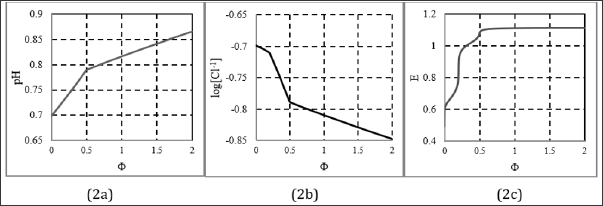
obtained from Eq. 12a, after omission of charged chlorine species/complexes. Moreover, [I2] < s, and then [I2(s)] = 0. Note that H3IO6-2 is the minor species in Eq. (37); its graph lies far below the plane of Fig. 1c. At Φ=2, we have pH(Φ=2) = 8.796 (Figure 1b); it results from reactions (33), (34), (36), where protons are consumed. The solution of KI is neutral, pH(⒃=0) = 7.00 in Figure 1b. Greater (but narrow) changes in pH and E values comprise, generally, the initial fragments of the respective curves in Figures 1b, c. The plots in Figures 2 & 3 were obtained at C = 0.2. The curves in Figures 2a, b is characterized by break points, whereas the curve in Figure 2c has inflection points. To explain the essence of these interest- ing changes, we will use speciation diagram (Fig. 3). The analysis of the course of the speciation curves will allow to formulate the reactions occurring at stages of the titration. A slope of the curve in Fig. 2a indicates greater consumption of protons at Φ < 0.5 than at O > 0.5. From Fig. 2b, we see that more Cl-1 ions are consumed within O ∈ <0.2, 0.5> than outside this Φ-interval. Moreover, the Cl-1 consumption within Φ ∈ <0, 0.2> and Φ ∈ <0.5, 2> proceeds in a similar degree. Within Φ ∈ <0, 0.2>, the main product (among I2Cl-1, ICl, ICl2-1) where Cl-1 is involved, is I2Cl-1. The reaction where I2Cl-1 is formed can be written as follows (Figure 3):
Figure 2: The plots of (2a) pH = pH (Φ), (2b) log [Cl-1] = φ(Φ) and (2c) E = E (Φ) relationships, at (C0, C01, C, V0) = (0.01, 0.2, 0.1,10).
Figure 3: The speciation diagram at (C0, C01, C, V0) = (0.01, 0.2, 0.1, 100).
IO3-1 + 5I-1 + 3Cl-1 + 6H+1 = 3I2Cl-1 + 3H2O
For O ∈ < 0.2, 0.5 >, concentration of I2Cl-1 decreases mono- tonically while concentrations of ICl2-1 and ICl increased; one can write the reactions:
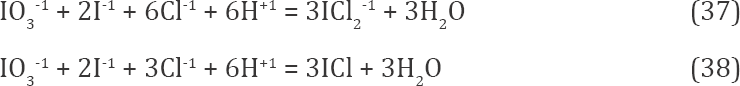
where Cl-1 is consumed in greater degree than within O ∈ <0, 0.2>, 6 >, compare Equations 37, 38 with Eq. 36; ICl2-1 predominates there significantly over ICl, see Figure 3. Within O ∈ <0, 0.5>, other iodine species: I2, I , and I3-1 are also formed
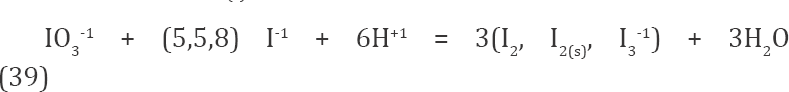
The number of protons consumed in reactions (36) - (39) is the same: 6. It explains the right course of the line in Fig. 2a within Φ ∈ <0, 0.5>. A decrease in concentration of I2Cl-1 on account of formation of ICl2-1 and ICl can be expressed by reactions: I2Cl-1 + Cl-1 = I-1 + ICl2-1 and I2Cl-1 = I-1 + ICl (where protons are not involved), obtained from linear combination of equations (36) - (38), respectively.
A precise location of inflection points on the E - E (Φ) curve (Figure 2c) is facilitated by derivative curves (Figures 4a & 4b). We see that the inflection points on the curve E - E(Φ) (Figure 2c) fit the related stoichiometric points exactly (Fig. 4a) or approximately (Figure 4b) - see location of break-points in Figures 2a, 2b and stoi- chiometries of reactions: 1:5 (in Eq. 36) versus 1:2 (in Equations 37, 38).
Figure 4: The ΔE/ΔΦ = (Ej+1–Ej)/(Φj+1–Φj) vs. (Φj+1+Φj)/2 relationships in the vicinity of Φ=0.2 (4a) and Φ=0.5 (4b), at (C0, C01, V0, C) = (0.01,0.2,100,0.1).
The D and T, when considered separately, are non-redox-sys- tems; ONs for I are: -1 in KI, and +5 in KIO3. The -1 is the lowest, boundary value of ON for iodine. On the other hand, +7 (not +5) is the highest, boundary value for iodine. However, the species: H5IO6, H4IO6'1 and H3IO6'2, represented by the numbers: N13, N14 and N15, were not involved in Eq. (30). This omission resulted from the fact that at E ≈ 0.5 V and pH ≈ 7 (Figures 1b, c), concentrations of the iodine (+7) species are extraordinarily small. It testifies because of the assumption that iodine (+5) species: IO3_1 and HIO3 do not disproportionate, practically, in KIO3 solution, and the simplified balance (30) is valid. The iodine (+7) species were involved in the balances related to D+T system, see section 3.
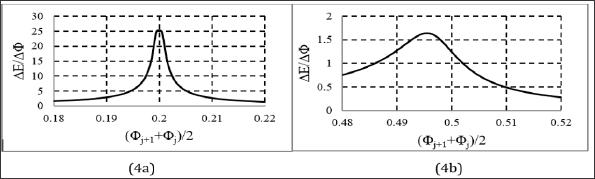
Figure 5: Speciation diagrams for mixed species: I2Cl-1, ICl, IC12-1 at (C0, C, V0) = (0.01, 0.1, 10), and: (5a) C01 = 0.2, (5b) C01 = 5.0.
In the model applied for the D+T system, the iodine and chlorine species with different ONs were involved a priori. However, the Cl-1 ions introduced by HCl (C01) practically do not participate as a reducing agent in this system; they act, however, as a complexing agent for iodine, depending on the concentration of C , compare Figures 3 & 5. Analogous situation was stated in the D+T system HCl NaIO, considered in [12, 18-20]; HCl acts in this system (first of all) as the component providing H+1 ions. Nota bene, the D+T system HCl NaIO is a simple example of electrolytic system, where all four types of chemical reactions, i.e. redox, acid-base, complexation (I2Cl'1, ICl, ICl2-1) and precipitation (I.) occur simultaneously.
Referring to the main problem raised in the title of this paper, we summarize and generalize the remarks stated above. From K+1 starting balances: f0, f1, f2, f3, ..., fK, after linear combination f - 2-f2-f1 we obtain the set of K balances: f0, f , f3, ... , fK. In the linear combination procedure, the identity 0 = 0, obtained from linear combination of balances, indicates that the equations involved in the combination are linearly dependent, i.e., they are not linearly independent. In a non-redox system, f is the dependent balance; we have their K-1 independent balances: f0, f3,..., fK. In other words, f12 is not a new, independent balance in non-redox systems; f is then omitted in formulation of any non-redox system. In a redox system, any linear combination of the balances f0, f1, f2, f3... , fK is different from (is not reducible to) the identity, 0=0, i.e., f is the independent balance. Then in a redox system we have K independent balances: f0, f12, f3, ..., fK.
The difference between redox and non-redox systems is then ‘coded’ in f . This unique, general property explains clearly why the elemental balances: f and f2 are not formulated for non-redox systems, of any degree of complexity. In conclusion, the linear independency/dependency of f - 2-f(O) - f(H) from other balances: f0,f3,...,fK is the general criterion distinguishing between redox and non-redox systems [13,22-24], also in mixed-solvent media [2,25]; the proper linear combination, with dk equal to ON’s, is the way towards the simplest/shortest form of GEB; for a non-redox system, it is the way towards identity 0 = 0. These remarks coincide well with the quotation ascribed to Einstein: ‘Everything should be made as simple as possible, but not simpler’. Transformation of a set of equations into the identity, 0 - 0, is a relatively simple/efficient/ useful operation when applied to the system of algebraic equations related to non-redox electrolytic systems [23].
In a redox system, f is considered as the primary form of Generalized Electron Balance (GEB), f = pr-GEB. The linear combination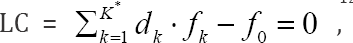
with balances for K* elec- tron-non-active elements (fans) has full properties of GEB. Any linear combination of the LC with K - K* balances for electron-active elements (players) can also be made. Other linear combinations of the K balances for redox systems, although acceptable (from an accounting point of view), devoid of motivation. Two equivalent (Eq. 24) approaches to GEB, known as the Approach I to GEB [26-34] and Approach II to GEB were formulated. The equivalence (24) is valid for redox systems of any degree of complexity, where one, two or more electron-active elements are involved. Formulation of GEB according to Approach II has - undoubtedly - the cognitive advantages, even in the cases when the oxidation numbers for all elements in the system are known beforehand.
In all instances, the balances are ultimately expressed in terms of molar concentrations [mol/L] of compounds and species, like the expressions for equilibrium constants. The related algorithm, with all attainable/complete physicochemical/thermodynamic knowledge involved in it, is resolvable with use of an iterative computer program, and then presented graphically. The Approach II to GEB does not require any prior knowledge of the oxidation numbers (ONs) of elements in the components and in the species; it is a fact of capital importance, particularly in relation to organic species (molecules, ions, radicals and ion-radicals), of any degree of complexity, also in two-phase systems [15,27,35]. Note that the oxidation number was essentially the contractual concept [36-38], based on arbitrary assumption that even the small difference in electro-negativities of atoms makes ionic bond between the atoms. However, the 'clean' ionic bonding does not exist, i.e., polar covalent bonds are formed. Even for CsF, i.e., for the compound with the greatest electronegativity difference 4.0 - 0.7 = 3.3 in the Pauling scale, we have 92% ionic bond, i.e., no compound can be 100% ionic. From the viewpoint of the Approach II to GEB, the ONs values are defined as multipliers of the corresponding linear combinations (Eq. 8a).
Some kinetic effects involved with organic compounds can also be tested [39]. The dynamic buffer capacities [40] in the form analogous to dynamic buffer capacity in acid-base systems [41,42] were also formulated. From the GATES/GEB [1,3-8,10-16,43-46] viewpoint, the terms: oxidation number, oxidant and reductant, equivalent mass [8] are derivative terms [47], not necessary (not applicable) for considerations on a redox system. Within the Approaches I and II to GEB, the roles/terms of oxidants and reductants are not assigned a priori to individual components; GATES/GEB provides full 'democracy' in this regard. If the oxidation numbers are easily determined, the Approach I to GEB, known as the 'short' version of GEB, can be applied. The Generalized Electron Balance (GEB) completing the set of equations necessary for resolution of electrolytic redox systems of any degree of complexity is a general law of Nature [3], one of the laws of the matter conservation. The GEB, together with linearly independent set of charge and concentration/core balances, completed by a set of independent equilibrium constants, provides a complete set of equations used for thermodynamic description of a redox system taken for quantitative considerations.
Within GATES, we refer to closed electrolytic systems, separated from their surroundings by diathermal (freely permeable by heat) walls; a matter cannot be exchanged by these walls. A proper heat exchange through diathermal walls enables the temperature T of the system to be kept constant, i.e., processes in the closed system can occur under isothermal conditions. Constancy of temperature, T = const, is one of the assumptions needed to secure constant values of the related equilibrium constants, defined based on mass action law. In principle, the diathermal walls separate condensed, e.g., liquid, liquid+liquid [27,48] or liquid solid [1,6,11,18-20,35,39] phases from its gaseous environment. An open chemical system approximates the closed system - provided that the matter (e.g., H2O, CO2, O2) exchange between the system and its surroundings can be neglected, within a relatively short period of time assumed to carry out the dynamic process, e.g. titration. The GATES is perceived as the unrivalled tool applicable, among others: (a) to mathematical modelling of thermodynamic behavior of the systems, (b) in choice of optimal a priori conditions of chemical analyses, and (c) in gaining chemical information invisible in real experiments, in general.
All the inferences made within GATES/GEB are based on firmly established physical, physicochemical and algebraic foundations. Consequently, it allows to understand far better the physicochemical phenomena occurring in the system in question and improve some methods of analysis. All the facts testify very well about the potency of simulated calculations made, according to GATES, based on all attainable and preselected physicochemical knowledge involved. Contrary to appearances, established by the current paradigm, the criterion distinguishing non-redox and redox systems is not immediately associated with free electrons in the related system; it provides a kind of uniformity in the formulas derived for this purpose. This fact, especially the simple calculations [11] of free electron concentrations in redox systems, deny the unique role of free electrons in elementary redox reactions, as described in half- or partial reactions, where the species of the same element with different oxidation numbers are involved. On the other hand, it points to the unique role of H and O in redox systems, suggested in earlier theoretical/ hypothetical/qualitative considerations on these systems. Let's repeat: the GEB concept, valid for redox electrolytic systems, is the emanation of balances for H and O, referred to aqueous media.
Abstract
PDF
