Quantifying Emotional Energy from a Physics Perspective Volume 63- Issue 5

Alexander Harrison*

• Fmr. Professor of Engineering, Newcastle University, NSW, Berkeley Computational Research, Berkeley Vale, NSW 2261, Australia

Received: November 11, 2025; Published: November 19, 2025

*Corresponding author: Alexander Harrison FRSN, Fmr. Professor of Engineering, Newcastle University, NSW, Berkeley Computational Research, Berkeley Vale, NSW 2261, Australia

DOI: 10.26717/BJSTR.2025.63.009968

Abstract PDF

The total energy describing a person’s feelings may be modelled in a similar way to inanimate bodies in which their energy is the sum of kinetic and potential energies. Since all bodies in the physical world conform to the energy law of physics, a person’s emotional and attraction feelings are quantified in relation to energy. A conceptual mathematical model is developed from psychology’s understanding of consummate feeling, combining physical and resonance energy to model a person’s dynamic energy. A visualization model using emotional “jolts” that modify the emotional states are proposed for an individual. The larger question of the influence of another person on one’s individual energy state is addressed by defining a stability criterion for entanglement energy between two people.

Keywords: Emotion; Personal Energy; Consummate Feeling; Physical and Resonance Feeling; Human Emotions; Models; Energy Jolts; Entanglement

Human understanding of abstract concepts such as feelings and emotions has been debated for eons by all tribes and cultures, as described by Darwin [1]. Understanding the connections between people that involve emotions is a complex field of psychology. Psychologists have studied human emotions for centuries with various interpretations related to parental effects and societal influences. Concepts such as closeness, trust, gut and heart feelings, love, desire, hate and body urges including hunger, procreation and even greed are emotions with complex interactions within a person and between people. Emotions are regularly discussed in relation to “who we are” as humans. Philosophical concepts naturally evolve from a human endeavor to understand ourselves. Plato produced philosophical treatises about desire versus spiritual love [2]. Schopenhauer viewed love as a metaphysical illusion driven by reproduction [3]. Many of these concepts have become embedded in religious doctrine and societal laws. Psychologists have attempted to define categories into which feelings may be broadly addressed. Hazan and Shaver researched Ainsworth’s bonding patterns and attachment styles related to romantic relationships [4], while feelings that stem from physical intimacy and somatic attraction have been researched by Siegel, et. al. [5,6]. Sternberg (1986) developed a triangular theory of love, where the concept of consummate or integrated love is a sum of somatic attachment or physical intimacy (given a symbol A), emotional intimacy or resonance (given the symbol R) and commitment (symbol K) [7]. At a mathematical level, work by Fry applied probability and game theory to model relationship longevity [8], while Suksasilp researched a framework of multi-dimensional interoception [9]. In all cited cases, no research exits that define an underlying basis to quantify in a mathematical way the interacting emotions alluded to by Sternberg. Indeed, emotions and attraction can be statistically modeled to describe the evolution of feelings in any given population. So how can emotions be modelled? To begin, use of descriptive symbols to describe a total emotional state, such as those proposed by Sternberg, may be a useful starting point in development of any model. Once an emotions-based model is developed at a mathematical level, the models can be tested by experiment or inputs from laboratory data. A particularly important development would be the derivation of equations describing the way individual and interpersonal connection can occur at a physics level. A procedure needs to be proposed to elucidate a fundamental mathematical model to describe emotional dynamics and emotion-related energy within and between people.

In a modern world of computing using mathematical algorithms, the question arises as to whether one can define emotions within a mathematical framework? Developing an “integrated emotion” equation would represent a new way of describing ourselves. More importantly, if an emotional coupling mechanism could be formulated that considers people’s interacting emotions, the mathematical description would have an even greater impact in understanding of humanity and connection with other people. This paper develops an energy balance model from physics to extend Sternberg’s emotional triad theory into a quantifiable form that can test psychological theories in a visual way. A basis for defining a person’s emotional energy that encompasses both individual and connected emotional energy is developed. An inter-personal energy coupling is further considered to explain, at a mathematical level, how people can influence others based on entanglement energy [10].

Prior research in the field of emotional psychology has laid a framework for the terminology of emotion theory applied to individuals and to some degree between people. In the Introduction, somatic attraction is referred to using the symbol “A”, while emotional intimacy uses the symbol “R”, capturing the embodied neurological basis for physical love and dynamic or bidirectional emotional attachment, respectively. Sternberg’s equation was formulated as L = A + R + K to define a total or consummate form of love. The term K may be questionable as an emotion, so it may be truncated from Sternberg’s definitions. Emotional interactions of all types are observable between people all the time. Many concepts exist to support a multidimensional view of emotional experiences. Sensing internal bodily states (e.g., heartbeat, gut tension) is termed “interoception”. Affective neuroscience describes how bodily urges and visceral feedback shape emotions [11]. Embodied cognition further describes how physical sensations influence desire, intuition, and decision-making [12]. Many questions arise as to how the mind and body work together to impart an emotional response in others. Humans know such emotional interactions are immediate, they may take the form of a gut feeling, body language or a blush [13]. As indicated, no scientific formulation exists to enable higher-level research on the dynamics of feelings and emotional energy. A great deal of knowledge exists in psychology and sociology fields that discuss observations and even body responses, including gut signals or feelings, measurements of brain activity and maps of emotions [14-18]. The descriptive equation of integrated feeling put forward by Sternberg shows considerable value in understanding the feelings of an individual but doesn’t address the influence of one person on another’s feelings. Indeed, many in the field of psychology might argue that that you are not responsible for the way others feel. The concept may not be true if it can be shown mathematically that a couple can interact at an energy level, even though we don’t know how to measure such interaction at this time [10].

In model development, one has to assume a condition where an individual can self-generate conditions from their own sensory inputs that cause them to experience their own feeling, and hence emotional energy. In that scenario, the total emotional energy L of one person should not influence the emotion of another being, unless there is some inter-coupling mechanism. In other words, a model needs to accommodate unknown interactions that people experience like body language or other thoughts like premonitions. As a reader will appreciate, emotional energy is a complex set of interacting concepts in psychology. An energy approach to human feeling has to be considered even though in psychology the use of an energy field has not been considered. A possibility exists that charge measurement via ECG tests is just a physical form of inherent energy transporting charges in animate beings. In order to consider a person’s attachment and somatic energy, a first step is to review known ways to define energy. Energy and particularly emotional energy are dynamic, meaning variations in energy may occur. In extending the conceptualization of energy as a way to define emotions, one could expect that there may be need to incorporate time-dependent emotional “jolts” into any model. Jolts from external events, such as a touch, bad news, a happy finding, would introduce peaks or losses in the energy relative to a baseline. From a model perspective, variations in the energy level of a body, which includes a person, introduces dynamic effects in their total energy. Energy is a well-known and easily understood entity in physics, therefore to cross-couple concepts in psychology with those of physics would be a natural progression.

In classical mechanics, the total energy of a single body 𝐸 is defined as the sum of kinetic energy K (the energy of motion), and potential energy U, which is the energy stored due to position or configuration. Without the addition of any coupling energy fields connecting other bodies, a single body has a total energy E = K + U. The equation is analogous in form to Sternberg’s emotional states L = A + R, implying that physical energy E in physics may be applied to describing emotional states. The energy equivalence in an emotional state would stem from fields that drive charge propagation in biological beings. A mathematical treatment defining a person’s emotional energy begins by supposing the person’s energy equation L described above equivalently describes the total emotional energy of a person. The energy for A originates as embodied tactile and neurochemical processes. The kinetic or driving energy R, is attributed to affective resonance, the physical attachment of emotional states like empathy and co-regulation. Clearly the concept of describing theories in psychology with a mathematical approach is feasible in this context.

Emotional Dynamics

Consider total emotional energy over time as a change of state of an average level of feeling. Discounting the influence of commitment K as an undefinable energy initially, the general form of Sternberg’s equation L = A + R becomes the sum of components A and R of a time-dependent energy function:

where A(t) is a somatic attraction energy with i representing one of the various feeling types, and R(t) is one of the affective resonances or physical attachment types of an emotional state k at time t. Each component has a baseline level at a given instant t, and responds to emotional jolts (positive or negative) caused by perception from external or internal inputs that decay or recover over time. On the basis that, at any time, emotional energy can suffer a jolt that may increase or decrease the energy. Jolts may result from a surprise or bad news, respectively. Suppose a positive jolt occurs at time 𝑡₀, causing an instantaneous increase ΔA or ΔR, which then decays exponentially back to baseline A₀ or R₀ respectively;

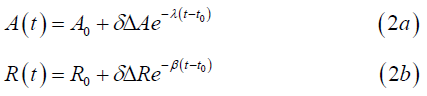
when time 𝑡 ≥ 𝑡₀, and where ΔA or ΔR > 0 represent the magnitude of a jolt. In equation (2a), λ > 0 is the decay rate of a body jolt, β > 0 is the decay rate of a heart jolt, and 𝑡₀ = time of jolt. The symbol δ is a switch with the conditions δ =1 for a positive jolt and δ = -1 for a negative jolt. In the case of a negative jolt to the persons energy, a drop in A or R occurs, followed by recovery back to baseline. This formulation ensures that A(𝑡) and R(t) return to a baseline as 𝑡 → ∞. Given that life is full of emotional jolts at time instances “i or k”, the solution is simply treated by generalizing each component as a sum of jolts:

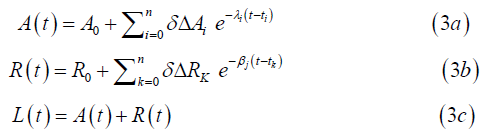
and each ΔA or ΔR may be positive or negative, at each 𝑡ᵢ or 𝑡k respectively at the time of a jolt. Each λ or β is the decay/recovery rate of the A or R field respectively. Equation (3c) captures the total dynamic emotional landscape of an individual suffering the feeling, which consists of a superposition of jolts, each fading or recovering over time. With respect to a baseline level of both A and R, there is no guarantee that these baseline levels remain constant over time. Rather than just looking at exponential decay, addition of long-term effects of recovery need to be added to the model to give a more nuanced effect into the time dependent A(t) and R(t) functions. A simple way to handle these baseline shifts over time is to replace constants A₀ =A₀(t) in equation (2a) and R₀ =R₀ (t) in equation (2b) so that the constants are replaced by a time-evolving variable. Gradual increase functions are;

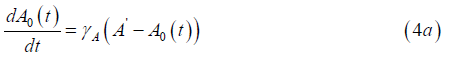
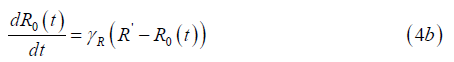
where γ is a growth factor representing how quickly the baseline improves, A’ and R ‘are ideal stable values achievable through healing and growth. As an emotional situation improves one would expect that A₀ and R₀ would asymptotically approach A’ and R ‘. With the above approach, this modification to baseline emotions of passion A (e.g. body) or emotional resonance R (e.g. heart) means past damage isn’t permanent, even if temporary jolts decay at differing rates. For example, a touch may cause a jolt in a person’s feeling that lasts a few minutes, whereas a bad news input may last days. The individual’s overall energy gradually strengthens if the individual experiencing the emotion improves over time. At present, analysis assumes no influence of person P2 on person P1. At present, a person’s energy state assumes it is all within themselves, with nothing “leaking out” to influence another person.

Discretized Recurrence Solution for an Emotional Jolt Discretizing a time-domain solution provides a method for rapid computer simulation and graphing of a dynamic process. The recurrence method of reducing ordinary differential equations into iterative recurrences is a valuable tool in mathematics [16]. For a continuous emotional jolt to body energy shown by equation (2), a discretization into time steps of size Δt is performed with a time incrementing time step t_n = t₀ +n Δt . The exponential decay can be approximated by a geometric progression, γ =e^−λ_iΔt ,and for Δt =1 which is a unit step size, then the recurrence pair for a body attraction jolt A and an emotional heart jolt R emotion is;

where ΔA[n] and ΔR[n] are the body and heart jolt feeling levels remaining at the nth time step, respectively. In both cases, a positive emotional jolt decays by a constant multiplicative factor α or β, respectively. If the jolt is negative, the same process occurs except the level grows back towards the respective baseline. Recurrence for a Time Variable Baseline in A or R An arithmetic recurrence (baseline recovery) is applied to the set in equation (4), as follows;

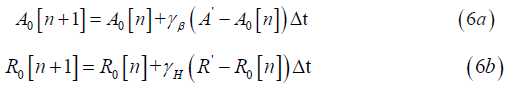
and for a unit step of the iteration, Δt =1. In equations (6), the value of the baseline recovery value in A₀

or R₀ is iterated at step (n) to calculate the new value at the next step (n+1). The relation pair makes an arithmetic adjustment toward A’ or K’ at t every iteration step, which is the discrete analogue of the continuous recovery process.

Overall Discrete Model for Jolts and Baseline Shifts

In analysis, use A[n] when calculating total body energy at time n, and A[n+1] when recursively updating A[n]. Using the above recurrence relations, the model for body emotion, incorporating both the evolving baseline and multiple jolts at the current time step n, is;

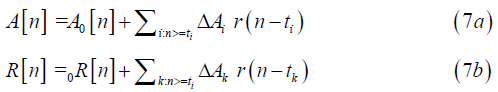
where each ΔA_i and ΔR_k could, for example, represent a body or heart jolt at a discrete time t₁, and r^{(n-t_i )} captures the geometric decay of the jolt over the (n - t_i) time steps following its occurrence. If the emotion being evaluated is, for example, body and heart emotion, then a body desire is only one part of the overall emotion, in which a heart emotion might apply. So, for the single emotion like love, variable A(t) becomes B(t) while R(t) becomes H(t), as is used to define a total energy E(t) in a following example.

A Simulation Example

Visualizing the model is possible using a graph that calculates every value of equation (3). In the time-dependent emotional energy model, namely, L(𝑡)= A(𝑡)+R(𝑡), let’s assume that the heart energy R(t) is replaced by a H(𝑡), and body physical feeling A(t) is replaced by B(t) since the equations are general and can be used to visualize feeling labels in any way. In this example, arbitrary values are chosen to show how the value of L(t) ≡ E(t) evolves under modeling conditions. Future researchers can use real laboratory values or other values based on psychological evaluation or physical testing methods. To illustrate the model’s application, parameters for the emotional energy equation are provided for body and love emotions as examples. A person experiences a rising body feeling of the baseline wellbeing from 60 units at t = 0, rising up to t=20 minutes. At t=20, a 40-unit jolt occurs in wellbeing from a good “phone call”. The parameters with a positive jolt at t = 20 are as follows:

𝐵₀ = 60; 𝐿₀ = 40; Δ𝐵 = +30 at 𝑡₀ = 2; Δ𝐿 = −20 at 𝑡₁ = 20; λ = 0.5; B₀(t) = 0.3t; H0(t) = 0.2t
For 𝑡 < 20, 𝐵(𝑡) = 60, thereafter, 𝐵(𝑡) = 60 + 30 ⋅ exp (−0.5 (𝑡 − 20)).
Parameters for a negative jolt in a heart emotion such as love, at t = 50, are as follows:
For 𝑡 < 50, H(𝑡) = 40, thereafter, H(𝑡) = 40 − 20 ⋅ exp (−0.5 (𝑡 − 50)).
Total emotional energy for 𝑡 ≥ 50 is:
𝐸(𝑡) = 60 + 30 ⋅ exp (−0.5 (𝑡 − 20)) + 40 − 20 ⋅ exp (−0.5 (𝑡 − 50)) +B₀(t) + H0(t)
For 𝑡 < 20: 𝐸(𝑡) = 60 + 40 = 100+ B₀(t) + L₀(t)
For 20 < 𝑡 < 50: 𝐸(𝑡) = 60 + 30 ⋅ exp (−0.5 (𝑡 − 2))
Figure 1 shows the graph simulating emotional dynamics using a hypothetical example with the above parameters. At 𝑡 = 20, body energy spikes to 𝐵 = 93, then decays toward 66. At 𝑡 = 50, a heart emotional feeling dips to H = 10 after rising gently from 40 to 50 over a 50-minute period, followed by a slow recovery near 30. Total emotional energy 𝐸(𝑡) reflects the sum of these two emotions of body and heart, including baseline shifts and emotional jolts. Clearly, more frequent jolts would lead to a more elevated E(t).

Figure 1

Discussion

The above analysis relates to the energy dynamics for a single person. Analysis of the dynamics of emotion for a single individual have not been related to other people with regard to any coupling mechanism between people. Without introducing a coupling mechanism between people, an individual’s feelings cannot affect or force an emotional response in the other. The effect of an emotion being modified by another person needs to be addressed for completeness. Addressing such a coupling influence would imply that an individual’s emotion is not solely self-generated and that their emotional energy may be affected by an external source. The mechanism of energy transfer between people requires further exploration. According to the model, a person’s total emotional energy L(t) consists of a sum of energies from A(t) and R(t), where both energies may consist of multiple components of differing emotions. In the above simulation example, only body feeling and heart feeling were modelled, however the equations allow for the computation of L(t) with multiple emotions added together within each component. The model shows that total emotional energy of a person can consist of a baseline with continually fluctuating jolts from life events. As discussed, the model doesn’t address connections between people.

Can there be an emotional connection between people such as experienced from a nearby person’s body language or thoughts? Can a person’s heart race by a body thought (e.g. of an impending meeting) or some anxious moment or feeling caused by another via precognition or a premonition? [10]. Prior research shows that two people can have a connection through the process of entanglement, where one person affects another’s ideas or feelings. The connection could take to form of information transfer from a nonlocal source such as a premonition. The idea that a condition can exist in the fifth dimensional realm that can immediately affect knowledge in the fourth dimension has been previously researched. From the discussion so far, total emotional energy will include somatic, physical and sensory-affective resonance components like those described in psychology. Kinetic energy could include emotional, relational, desire, love or feelings of the gut and heart, and perhaps even spiritual components. Compared to classical mechanics, A(t) represents the potential energy of embodied, tactile and neurochemical drivers including embodied experience (touch, presence, sexual bonding). The R(t) value, equivalent to kinetic energy captures deeper, unexpressed physical affective resonance.

If a coupling filed Uint is added between Persons P1 and P2 as suggested earlier, then one might expect that coupling equations might take the static form L₁ = A¹ + R¹ + U^int1, and L² = A² + R² + U^int2. The dynamic form would include time dependence terms forming L₁(t) and L2(t). The question as to what degree can one object interact or influence another object or set of objects is not clear in human understanding. Even though people report “feeling” something between each other, how is that feeling or energy transferred as information in a mathematical sense? Consider an inter-personal connectivity process across spacetime. Specifically, connection through nonlocal entanglement that is not related to gravitational or electromagnetic effects. A new fifth dimensional field Q has been proposed to explain how information can present itself instantly or from a future domain [10]. A starting point for analysis of the new field between 2 people requires that a connection exists by an entanglement mechanism. Considering the earlier definition of a person’s true emotional energy being a sum of a body energy and feeling energy, a natural extension would be to examine the application of entanglement.

An Emotional Entanglement Field

Introducing a fifth-dimensional nonlocal field Q that connects two persons P₁ and P₂ through emotional entanglement permits analysis of connectivity between people. The field Q is used to describe the emotional states of P₁ and P₂. A phase difference in emotional resonance Δφ can be part of a function ƒ, so that the field Q = ƒ (L₁, L₂, Δφ) where L₁ and L₂ are the total emotional energy states of P₁ and P₂ respectively. The interaction potential VQ, mediated by the field Q, is defined as;

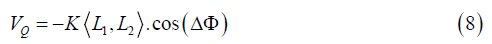
where k is the entanglement coupling constant, 1 2 L , L is the dot product of emotional vectors, and cos(ΔΦ) captures the phase coherence. Since Q is a fifth-dimensional nonlocal field, a classical time variable t may not be appropriate. Instead, introduce a nonlocal evolution parameter τ, defined as in which Φ is a scalar function representing shared emotional depth or entanglement phase. Thus, the field simply becomes Q = Q(τ ). Emotional energy functions can be set up in general so that “A” defines a scalar field dependent on spatial proximity and orientation, i.e. A = A (r, θ) where r is spatial separation and θ is orientation of physical states. Define the emotional part R as a vector field in affective space where e₁ and e₂ are emotional components and γ is the coherence factor (such as trust, vulnerability or shared meaning).To extract the scalar intensity of R, compute the mathematical norm of R, i.e., that represents the total emotional depth between P₁ and P₂. Dynamics of the entanglement field Q occurs by summing emotion components to form a differential equation for the evolution of Q:

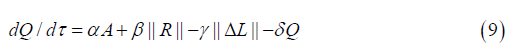
where α, β are positive coupling constants, γ penalizes emotional divergence, δ represents entanglement decay, and total absolute energy is a difference in equation (9), . Emotional states A and R respectively are allowed to evolve from the simple differential equation pairs;

using μ as the entanglement-to-body coupling parameter, ν is physical dissipation, 𝐂 is the coherence vector, ξ amplifies emotional growth via entanglement and ς = x represents emotional fatigue or misalignment. A dynamic triad forms a closed-loop system Q ↔ A ↔ R. Each component energizes and regulates the others, forming a dynamic model of emotional entanglement. One may explore equilibrium and stability conditions for entanglement of the triad, by investigating how the derivates evolve. Assuming that the closed-loop system is at equilibrium, meaning all derivatives with respect to the nonlocal parameter τ are zero, then . Derivates applied to equation (9);

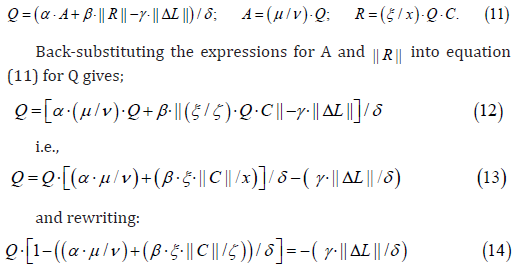
An entanglement condition between two people must ensure Q > 0, therefore the left-hand side must be negative (since the right-hand side is negative). This implies that entanglement feedback strength;

which is an entanglement threshold condition. If the combined feedback strength exceeds the decay rate δ, and emotional divergence || ΔL is sufficiently small, then Q > 0, proving that emotional entanglement is present and self-sustaining between P₁ and P₂. in summary, if the combined feedback strength exceeds the decay rate δ, and emotional divergence || ΔL || is low, then Q > 0 implies P₁ and P₂ are emotionally entangled. This is because Q is generated and sustained by mutual coupling through A and R, and its persistence reflects a nonlocal connection between the two individuals, that is, entanglement exists and information transfer can be instant as a premonition feeling.

Visualizing the Entanglement Between People

From the above analysis, the threshold condition may be graphed to show how Q behaves as a function of feedback strength and emotional divergence. Recall that emotional entanglement was defined as the existence of a fifth-dimensional field Q that is non-zero, Q > 0, is self-sustaining so it remains positive over τ without external forcing, is bidirectionally coupled to a body emotion A and heart feeling R. Analysis further implies that Q is not a transient or random fluctuation, but a persistent field generated by mutual emotional and physical resonance. Equation (15) effectively defines the equilibrium expression as Q = Q_e. A graph of how Qₑ behaves as a function of emotional divergence || ΔL || is shown in Figure 2. The horizontal axis shows emotional divergence || ΔE || , representing misalignment between emotional states of P₁ and P₂. The vertical axis is entanglement strength Qe, showing how strongly the field Q binds the two individuals. This graph confirms that Qₑ > 0 only occurs when the system satisfies the threshold condition (α ⋅μ /ν ) + (β ⋅ξ ⋅ ||C || /ζ ) >δ for an instant feeling between two people, including premonitions.

Figure 2

Defining a person’s emotional energy from a physics perspective supports a multidimensional view of the emotional experience experienced by humans. When emotions are connected, a criterion for entanglement shows that nonlocal information transfer can exist instantly between people, giving rise to premonitions when people are spatially separated. Interoception involves sensing internal bodily states (e.g., heartbeat, gut tension). Affective neuroscience describes how bodily urges and visceral feedback shape emotion, while embodied cognition details how physical sensations influence desire, intuition, and decision-making Perspective views between psychology and physics converge when a mathematical treatment of a psychological description can be elucidated. Psychologists quantify love’s components and dynamics, whereas mathematicians model its dynamics and patterns. Philosophers are left to interrogate its meaning, ethics, and existential role. The research shows that an equivalence can be drawn between energy in physics and emotional energy of a person and between people. A person’s emotional ups and downs may be modelled as variations in the baseline level of one or more emotions. The “ups and downs” have been modelled as energy jolts on the baseline levels, giving some insight into ways of visualizing the evolution or dynamics of a particular emotion. Similarly, modelling how these jolts may persist, grow or decay at different rates affects the baseline where an emotion settles before the next jolt. These methods are considered verifiable with suitably devised laboratory experiments. Philosophers, psychologists and even mathematicians have explored love before, but none have provided a quantifiable model for trust recovery, emotional jolts or baseline shifts with exponential decay and with a capability to model gradual repair.

As such, the modelling in this paper might be considered as a fusion of mathematical precision with human relationships, almost like how we model physical phenomena or population growth. Development of a kind of mathematical psychology for one aspect of emotions, love, could have implications and real applications in understanding how relationships strengthen or deteriorate over time, and how others may influence the outcome of a person’s emotion. Introducing the concept of energy to describe emotional states of a person has provided a way to develop a quantitative model that can be tested by experiment and measurements. The concept that one person cannot affect the emotional states of another or is not responsible for the other’s feelings should be reconsidered based on these findings. Entanglement theory shows that a threshold condition exists to prove a nonlocal transfer of information, instantly, such as through a premonition or with a precognition delay. The research indicates that people can sense each other’s feelings across spacetime. Future research can aim to discover ways of measuring and proving the mechanism of entanglement between people.

1. Darwin C (1872) The Expression of the Emotions in Man and Animal. London: John Murray. (1^st)., Book, pp. 398.
2. Plato (n.d.). Symposium. Translated by Benjamin Jowett.
3. Schopenhauer A (2010) The World as Will and Representation. Translated by J. Norman, A. Welchman and C. Janaway. Cambridge: Cambridge University Press. Chapter 44: Metaphysics of Sexual Love 2.
4. Hazan C, Shaver PR (1987) Romantic love conceptualized as an attachment process. Journal of Personality and Social Psychology 52(3): 511-524
5. Siegel DJ (2012) The Pocket Guide to Interpersonal Neurobiology: An Integrative Framework of the Mind. New York: W.W. Norton & Company.
6. Carvalho GB, Damasio A (2021) Interoception and the origin of feelings: A new synthesis. DioEssays 43(6): 2000261.
7. Sternberg RJ (1986) A triangular theory of love. Psychological Review 93(2): 119-135.
8. Fry H (2015) The Mathematics of Love: Patterns, Proofs, and the Search for the Ultimate Equation. London: Simon & Schuster.
9. Suksasilp C, Garfinkel SN (2022) Towards a comprehensive assessment of interoception in a multi-dimensional framework. Biol Psychol 168: 108262.
10. Harrison A (2025) Human premonitions explained by nonlocal entanglement theory. UAR J Multdisciplinary Studies 1(8): 1-18.
11. Immordino-Yang MH, Damasio A (2007) We feel, therefore we learn: The relevance of affective and social neuroscience to education. Mind, Brain and Education 1(1): 3-10.
12. Barsalou LW (2008) Grounded cognition. Annual Review of Psychology 59: 617-645.
13. Nikolić M, di Plinio S, Sauter D, Keysers C, Gazzola V (2024) The blushing brain: neural substrates of cheek temperature increase in response to self-observation. Proc Royal Soc B 291(2027): 20240958.
14. Holzer P (2022) Gut Signals and Gut Feelings: Science at the Interface of Data and Beliefs. Front Behav Neurosci , p.16.
15. He Z, Li Z, Yang F, Wang L, Li J, et al. (2020) Advances in multimodal emotion recognition based on brain-computer interfaces. Brain Sci 10(10): 687.
16. Harrison A (2021) A single recurrence simulates growth cycles in nature. Int J Sci Res Multidisciplinary Studies 7(8): 01-07.
17. Nummenmaa L, Glerean E, Hari R, Hietanen JK (2014) Bodily maps of emotions. Proc Natl Acad Sci USA 111(2): 646-651.
18. Mauss IB, Robinson MD (2009) Measures of emotion: a review. Cogn Emot 23(2): 209-237.