Coupled Structure-Fluid Analysis of Fiber Shaking in Dry Spinning Volume 62- Issue 5

Tatsuhiro Yamamoto*

• Faculty of Human–Environment Studies, Kyushu University, Japan

Received: August 01, 2025; Published: August 08, 2025

*Corresponding author: Tatsuhiro Yamamoto, Faculty of Human–Environment Studies, Kyushu University, 744 Motooka Nishi-ku, Fukuoka City, Fukuoka 819-0395, Japan

DOI: 10.26717/BJSTR.2025.62.009814

Abstract PDF

The global automotive industry has seen an increase in battery electric and hydrogen fuel cell vehicles, which has been driven by incentives. Battery electric vehicles suffer from low-temperature performance issues and limited charging infrastructure, while fuel cell vehicles deliver high energy efficiency and zero tailpipe emissions, but they are hampered by sparse refueling networks and stringent safety requirements for pressurized hydrogen. Carbon fiber–reinforced composite tanks are produced using a dry-spinning process that has been stagnant since the 1990s. Current theoretical models treat solvent diffusion and convective transport separately. These models rely on empirical transfer coefficients and semi-empirical correlations, which reduce predictive accuracy and reproducibility. Here, the authors present a unified three-dimensional numerical framework that integrates convective-diffusive transport with fiber structural dynamics on a single computational mesh. Validation simulations reveal the impact of fiber vibrations on solvent removal kinetics and thermal profiles, demonstrating the model’s ability to capture coupled transport and mechanical effects. The framework’s novelty does not stem from new governing equations, as these have been detailed in earlier studies, but rather from adapting hemodynamic analysis methods to dry-spinning theory. Though the model is purely theoretical and awaits experimental validation, it provides patentable insights derived from industrial observations. Leveraging cross-disciplinary techniques promises to optimize high-throughput carbon fiber production and advance robust hydrogen tank design.

Keywords: Dry Spinning; Computational Fluid Dynamics; Numerical Analysis; Heat and Mass Transfer Equation; Fiber

In recent years, the global automotive industry has experienced an unprecedented acceleration in the development of battery electric vehicles (BEVs) and hydrogen fuel cell vehicles (FCVs). This growth has been driven largely by market leaders and supportive policy frameworks. Tesla’s rise has made BEVs particularly appealing to consumers [1] yet concerns about battery performance in cold climates continue to hinder widespread adoption [2]. Although the charging infrastructure has expanded significantly compared to a decade ago, it still falls short of meeting the surging demand in many regions [3]. Major economies, such as the United States, have announced plans to ban the sale of new gasoline-powered vehicles by 2035 [4], and Japan is pursuing a similar phased elimination strategy [5]. Meanwhile, Toyota Motor Corporation and other leading manufacturers have accelerated fuel cell vehicle (FCV) development and introduced commercial models to the market [6]. However, the scarcity of hydrogen refueling stations and the high barriers to entry for infrastructure providers remain significant obstacles to adoption [7,8]. Nevertheless, hydrogen fuel cell vehicles operate on a fundamentally robust electrochemical principle [9] and deliver high energy efficiency alongside minimal tailpipe emissions [10].

The safe operation of fuel cell vehicles (FCVs) hinges on pressurized hydrogen storage tanks. Their ability to withstand cyclical and extreme loading conditions is crucial for regulatory certification and vehicular safety [11]. Carbon fiber, which has been used for a long time in aerospace and military applications due to its exceptional strength-to-weight ratio [12,13], has become the preferred composite reinforcement material for these pressure vessels. Its various grades and customizable properties allow for precise optimization for pressure regimes and service lifetimes [14]. Its production involves several processes, from precursor synthesis to final heat treatment [15]. The production of high-performance carbon fiber relies primarily on the dry-spinning process. In this process, a polymer solution is extruded and the solvent is evaporated by hot air to form continuous filaments [16]. Although the process is industrially mature, it reached a technological plateau in the 1990s, resulting in relatively few fundamental studies in subsequent decades [17,18]. Recent academic efforts have focused on improving the quality of fibers at the laboratory scale, such as enhancing their crystallinity and surface morphology [19]. Traditional theoretical models emphasise radial solvent diffusion and vertical moisture transport, particularly when water serves as the solvent. However, these models fail to capture the coupled transport phenomena encountered in high-throughput production lines [20-22].

Conventional approaches to quantifying heat and mass transfer in dry spinning typically treat transfer coefficients as empirical fitting parameters derived from post hoc calibration rather than from a fundamental analysis [23]. These methods rely heavily on dimensionless Nusselt and Sherwood numbers and use semi-empirical correlations, which introduce inconsistencies and limit the precision of predictions for process design [24,25]. Conversion between convective regimes via proprietary adjustment factors is not transparent and hinders reproducibility of results [26]. For instance, heat flux estimations based on tire vertical oscillation experiments using Nusselt-number correlations have been demonstrated [27], and macro-scale building simulations often use Nusselt-based models without ensuring consistency with micro-scale computational fluid dynamics (CFD) findings [28,29]. To overcome these limitations, the present study introduces a thorough, three-dimensional numerical framework that unifies convective and diffusive transport phenomena with fiber structural dynamics on a single computational mesh [30]. Demonstration calculations validate the framework and clarify the impact of fiber vibrations on solvent removal rates and temperature distributions. This provides a solid theoretical basis for carbon fiber production and comfort index evaluations in vehicle interiors and architectural settings.

Dry spinning is a process in which the solvent, water, is removed by a combination of hot air and aerodynamic forces; however, controlling this process is extremely challenging. Although numerous patents have been filed, none include detailed accuracy verification, making experimental validation essential. This paper aims to develop a theoretical framework, since conceptual formulation and validation are key elements that justify undertaking costly experiments. Figure 1 presents a conceptual diagram illustrating cases involving airflow intensity and the natural vibration period of fibers. In the left panel, nonuniform airflow impinges on the fibers, causing periodic yet steady deformations in unexpected directions; thus, a semi-steady solution grounded in structural-mechanics insights is required. During solvent evaporation, the distance to alignment serves as an effective metric: while it enhances drying, it also induces fiber agglutination and degrades fiber quality. Therefore, the air-blowing system must be optimized to minimize deleterious vibrations. For example, airflow reduction might be achieved through dynamic breathing from a single surface or by exploiting porous-material characteristics via “fire-working” techniques; these approaches warrant careful experimental investigation.

Figure 1

In the right panel of Figure 1, a green auxiliary line indicates the corrected fiber deformation. Although this step advances the determination of actual fiber length and enables detailed heat-and-masstransfer calculations via the Theorem of the Square, fiber handling remains challenging due to their fragility, so thorough experimental scrutiny is imperative. As shown in Figure 2, it is difficult to follow the physical behavior of the fiber swing in the calculation if the wind flow path is not directional. Conversely, obtaining a steady-state solution is straightforward if the fiber oscillation can be considered periodic and stationary, provided that the rectifier is stable. This is because the steady-state solution can be easily calculated using the theorem of three squares and the principle of virtual work in structural mechanics. Although there may be some calculation errors, they are within the acceptable range. Please refer to our previous report [31,32] for details on the formulas and other information. However, this is an applied use of structural mechanics, like understanding the heat and mass transport of technical fibers, e.g., the evaporation of water as a solvent. Equation (4) quantifies the effect of longitudinal vascular oscillation per second and represents heat loss resulting from strain (σ), which is induced by external work on the vessel wall.

Figure 2

In this context, the applied strain (σ) can be predetermined by modelling a non-stationary response in structural mechanics via the principle of virtual work to accurately capture dynamic loading conditions. Alternatively, σ can be more simply computed by assuming that the distal end of the vessel is fixed and that there is no axial expansion or contraction along the x-axis, as illustrated in Figure 3. Under this assumption, the vessel’s heat loss is determined using equation 1, and the deformed vessel length is obtained using equation 3 and the Pythagorean theorem for strain displacement. Consequently, one can derive the instantaneous length of a vessel undergoing cyclical expansion and contraction. In these calculations, heat loss is presumed to be measurable and known. However, it is important to note that this approach requires sufficiently refined mesh discretisation in finite- element analyses to ensure convergence. In the present study, we focused on establishing a steady-state solution, which is a challenging computational task that requires iterative solvers. Given the availability of well-established nonstationary theories, we propose that transient modelling follows the development of steady-state methodology. As shown in Figure 3, an increase in the amplitude of structural deformation corresponds to greater vessel elongation, which directly affects heat loss during each distinct oscillation period.

Figure 3

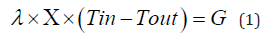
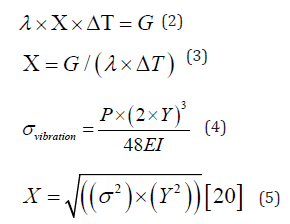
Assuming strain σ is determined via the principle of virtual work and the Pythagorean theorem (Equation 5) (Figure 4) the resulting deformation can be quantified, and the discrepancy between demonstrative and actual calculations can be assessed. Although horizontal flow-induced forces are present, they are omitted from this demonstration. The deformed length X is computed using the Pythagorean Theorem. Then, Equation (2) yields the corresponding heat transfer. Once σ is established, the oblique vascular deflection length follows from these thermomechanical relations. This result has already been confirmed by numerical calculation. Although incorporating horizontal blood flow would complicate the theoretical framework, excluding it under the present assumptions ensures error-free computations within the specified range.

Figure 4

Figure 5

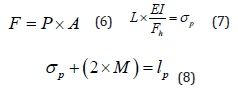
Figure 5 illustrates the new dry spinning process. First, drawing together is a critical factor in fiber quality. Therefore, the process carefully aligns the fibers with rollers in the direction of gravity after decreasing the moisture content. Otherwise, variations in fiber diameter may occur, associated with phenomena such as fiber agglutination. Thus, it is important to wind the material onto a bobbin after sufficient alignment. Additionally, preparing the wall surface of the porous body allows the “fire” from the breathing wall body to contribute to reducing the moisture content of dense fibers in the multirole process. However, the degree of adjustment is important. Figure 6 shows how to achieve stable spinning by adjusting the flow rate through a breathing wall or duct. Since the outlet flow rate varies depending on the duct’s path, a pressure-regulating valve is essential. The performance of the hot-air equipment also depends on the pressure loss calculation, so a professional in mechanical equipment design should oversee its selection. The adjustment function is important. Figure 7a illustrates the occurrence of “thermal fluctuation” in response to fibre oscillation (e.g., carbon fiber). The fibre oscillation is due to aerodynamic forces, and the oscillation appears like vibration. Therefore, it is necessary to reduce the discrete time to milliseconds. Figure 7b illustrates the appeal to “thermal fluctuation” of fibers by the next-generation unit system. We recently discussed the possibility of using J or g per unit temperature to define heat and mass transfer. The g unit is familiar because it is used to measure human body weight. Therefore, it is necessary to redefine how we understand water content. Thus, g is preferable as the unit of measurement for water content. Additionally, calculations with millisecond resolution may be necessary depending on thermal fluctuations or fiber shaking.

Figure 6

Figure 7

This study presents a comprehensive overview of a novel theoretical framework for accounting for fiber oscillations in dry-spinning numerical simulations, illustrated with schematic figures. The governing equations themselves are not new—they have been detailed in prior work—and demonstration calculations are likewise deferred to existing reports. The core contribution of this research lies in the persuasive cross-disciplinary application of hemodynamic analysis techniques to drive innovations in dry-spinning technology

As a purely theoretical proposition, immediate experimental success cannot be assumed. Nevertheless, the challenges addressed were extracted from empirical observations, and the underlying concepts possess patentable potential and significant novelty. It should be noted, however, that real-world manufacturing entails budgetary constraints and unforeseeable obstacles, and readers are kindly asked to consider these practical realities when evaluating the framework.

Numerical simulation of dry-spinning has appeared in several peer-reviewed studies, most of which rely on complex equations or partial differential formulations and thus lack practical simplicity. Dry spinning is inherently a Multiphysics process; by adapting methodologies from other disciplines, it is possible to tackle the intricate coupled phenomena highlighted in this work. Once a robust steady-state analysis is established, extending to unsteady simulations becomes straightforward, mitigating the need to prioritise transient modelling at this stage. In the near future, the realisation of highly resilient, rigid hydrogen storage tanks fabricated from carbon fiber is anticipated, underscoring the industrial relevance of advancing dry-spinning theory.

There are no conflicts of interest to declare.

1. (2022) Tesla, Inc. 2022 impact report. Palo Alto, CA (USA): Tesla, Inc.
2. Howell D, Browne M, Rodgers S (2020) Low-temperature performance of lithium-ion batteries for electric vehicles. J Power Sources 459: 227999.
3. Sierzchula G, Bakker S, Maat K, van Wee B (2014) The influence of financial incentives and charging infrastructure on electric vehicle adoption. Energy Policy 68: 183-194.
4. (2021) The White House. Executive order 14008: Tackling the climate crisis at home and abroad. Washington, DC: The White House.
5. (2020) Ministry of Economy, Trade and Industry, Government of Japan. Green growth strategy through achieving carbon neutrality in 2050. Tokyo: Ministry of Economy, Trade and Industry.
6. (2021) Toyota Motor Corporation. Launch of the second-generation Mirai fuel cell vehicle. Yokohama (Japan): Toyota Motor Corporation.
7. Peterson SB, Inman VA, Liu LP (2019) Fuel cell electric vehicle hydrogen infrastructure development: Costs, challenges, and solutions. Int J Hydrogen Energy 44(15): 7403-7419.
8. Peters M, Lam S (2020) Economic assessment of hydrogen refueling infrastructure deployment in urban areas. J Clean Prod 245: 118801.
9. Züttel A (2004) Hydrogen storage methods. Naturwissenschaften 91: 157-172.
10. (2020) U.S. Department of Energy, Fuel Cell Technologies Office. Multi-Year Research, Development, and Demonstration Plan. Washington, DC: U.S. Department of Energy.
11. Grzelakowski S, Saari G, Hjelm FD (2018) Fatigue and burst testing of composite hydrogen storage cylinders. J Pressure Vessel Technol 140(5).
12. Tognon E, Berto F (2015) A review on mechanical behavior of aerospace-grade carbon fiber composites. Compos Part A 74: 54-67.
13. Choi J, Sohn B, Kim J (2016) High-performance carbon fiber composites for military applications. Mater Sci Eng A 651: 85-98.
14. Ziemian M, Pecora T, Jastrzebska M (2019) Tailoring carbon fiber properties via controlled pre-oxidation and carbonization. Carbon 145: 102-110.
15. Kim K, Kim H, Lee S (2017) Manufacturing of carbon fibers: From precursor polymer to final carbonization. Polym Int 66(7): 425-433.
16. Eom TH, Yang JK, Lee SH (2018) Fundamentals of the dry-spinning process for high-performance polymer fibers. J Appl Polym Sci 135(23).
17. Hernandez JP, Zhang L, Wilson D (1995) Technological evolution of dry-spinning: Historical development and current status. J Fibers Textiles 12(4): 22–30.
18. Sanchez-Rivera L (1996) Advances in fiber spinning technologies: A comprehensive review. Polym Rev 36(2): 101-148.
19. Gupta A, Kumar R (2020) Laboratory-scale improvements in carbon fiber crystallinity via optimized dry-spinning parameters. Mater Lett 264: 127288.
20. Yamamoto H, Tanaka S, Sasaki K (2017) Modeling radial solvent diffusion in dry-spun polymer fibers. Chem Eng J 340: 355-363.
21. Petekidis M, Tsotsas G (2019) Moisture and heat transfer in dry spinning of water-soluble polymers: experimental and theoretical insights. J Membr Sci 578: 117000.
22. Sarwar F, Sundaram PK, Ghosh C (2021) Coupled heat and mass transfer in polymer fiber spinning: Experimental validation and modeling. Int Polym Process 36(1): 57-68.
23. Rao KR, Venkateshan SP (2016) Empirical correlations in convective heat and mass transfer: A critical review. Heat Transfer Eng 37(12): 1069-1087.
24. Dhir VK, Singh SK (2015) Dimensionless correlations in convective heat and mass transfer and their limitations. Int J Heat Mass Transf 80: 42-53.
25. Moore EJ, Hall FL, Brown RK (2018) Evaluation of dimensionless correlation usage in industrial drying processes. Dry Technol 36(3): 300-312.
26. Hanratty TJ, Dunn PF (2014) Uncertainty analysis of heat transfer correlations in chemical engineering design. J Heat Transfer 136(6).
27. Saberi AM, Higgins SA, Bishop LE (2015) Heat flux characterization from tire-soil interaction using Nusselt number correlations. Int J Therm Sci 90: 1-12.
28. Schiavon S, Yang B, Altoé V (2016) Application of Nusselt number correlations in whole-building energy simulation. Build Environ 100: 210-219.
29. Yang Y, Chen J (2020) Bridging microscale CFD findings with macroscale heat transfer models in building energy analysis. Energy Build 226: 110353.
30. Liu Z, Patel M, Xu H (2023) Three-dimensional modeling of coupled heat and mass transfer with structural dynamics in fiber spinning processes. Comput Mater Sci 204: 111029.
31. Yamamoto T (2025) Innovative theory of heat and mass transfer in dry spinning. Biomed J Sci & Tech Res 62(5): 009793.
32. Yamamoto T (2025) Human thermal comfort and pressure modeling in automotive seats: A practical approach for engineers and clinicians using structural mechanics and thermal science. Kyiv: ElivaPress, p. 1-43.