Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Shinichi Tamura1,2*
Received: July 24, 2025; Published: September 01, 2025
*Corresponding author: Shinichi Tamura, NBL Technovator Co., Ltd., 631 Shindachi-Makino, Sennan City, Osaka 590-0522, Japan
DOI: 10.26717/BJSTR.2025.62.009806
Diversity is an effective factor in evolution. Based on a previous study on the play instinct of artificial lives in which the author participated, this paper presents two theories that can quantitatively show how many LGBTQ+ (a typical diversity in humans) people there are. One theory reflects that the number of sexes that maximize evolution from a global, long-term perspective is e (Napier’s number = 2.71...), meaning that the number of sexes that will possibly be under pressure to become nonbinary is 2 or more. In addition, this paper presents a sex-aspect birth model that explains that LGBTQ+ people exist at a constant rate, although they appear to have difficulty producing offspring. This model posits that there still may be possibilities for human evolution. For this reason, LGBTQ+ people should not be excluded or discriminated against, but recognized as the result of a natural flow accompanying human evolution and should coexist with non-LGBTQ+ persons in an inclusive manner.
Keywords: Base-e; Discrimination; Evolution; Generational Change; Number of Sexes; Rate of LGBT; Sexual Orientation
The author was asked by the president of a company, “Why do people play”. This question probably arose from the desire to create a system in which said president’s employees could enjoy more actively their work. This led the author to begin researching artificial lives where play occurs as a hobby or for fun. The benefit of play itself has been summarized by Ellis [1], but the discussion remained on a nonquantitative level. The productivity and adaptability of human society, which is comprised of people with various genetic qualities, abilities, and preferences, were simulated through generational changes in a changing environment [2]. The results demonstrated that societies that include a large amount of play have a high ability to respond to and adapt to change, whereas societies that have a limited amount of play have a low adaptability. When a changed environment and people’s abilities match, they achieve high productivity; conversely, when they do not match, productivity decreases, and sometimes the human race itself becomes extinct. In other words, societies in which there are many opportunities to train people in required skills through play that do not appear to be directly linked to productivity are more likely to have stable productivity, despite changes such as the Industrial Revolution. It was also discovered that in a stable and developed society, each person has a greater variety of abilities and talents than they appear to, and play is the expression of these abilities. Simply put, a diverse society has greater adaptability to a changing environment.
Although the research began from the perspective of play, the same framework and conclusions can be applied if LGBTQ+ appearance is also viewed as a genetic characteristic of each person. In other words, if society accepts LGBTQ+ people as having diverse characteristics and abilities, it is posited that the productivity of society will improve, and this will have the effect of stabilizing society. Therefore, in this paper, to quantitatively analyze the extent of LGBTQ+-related diversity, we will study mathematics regarding the number of sexes in the process of maximizing the evolutionary rate from a broad and long-term perspective, and mathematics of short-term stationarity, in which LGBTQ+ people exist as a certain percentage of the population, even though they appear to have difficulty producing offspring.
Although sexual reproduction requires twice as much effort as asexual reproduction, its superiority under various changing environments has been demonstrated [3]. Further, paramecium have many sexes, and a paramecium with sixteen sexes has been reported [4]. Therefore, how many sexes are appropriate from the perspective of human evolution? In this paper, as an evaluation function where the number of sexes (complexity) is moderately small and the number of generations required for evolution is also small, the number of sexes whose these product is the minimum is derived. (Figure 1) shows a generational alternation model for humans with two sexes (N = 2). Where the number of individuals is x = Nd = 8, offspring with a combination of talent genes from all people will be born in d = 3rd generation. In a living organism (human) with three sexes, genes from three individuals combine to produce one child. Where x = Nd = 9 people, in the 2nd (=d) generation, talents from all individuals are combined, and progeny with a combination of genes will be born (Figure 2).
In reality, it is impossible for humans to combine all three bodies at the same time, but this is a hypothetical case including proportionally counted siblings. In a living organism with N sexes, it is desirable that the number of sexes (complexity) N is moderately small, and the number of generations d is small, producing offspring with the best combination of talents so that the evaluation of y = N × d, including the conflicting demands, becomes the smallest. By differentiating this y with N and setting it to 0, the N that minimizes y becomes N = e (Napier’s number), as in the e-base number problem. In reality, for example, it is almost impossible for three individuals to combine their genes and create a child, so the actual number of sexes is N = 2. However, the optimality of the number of sexes N = e = 2.71... becomes a natural pressure, which may lead to three sexes, a sex change, or LGBTQ+ appearance. (See Appendix Ap1)
Simply thinking, it must be difficult for LGBTQ+ people to produce children. However, there is always a percentage of LGBTQ+ people in the population. Recently, a large-scale genetic analysis of nearly 500,000 people revealed that although there appears to be a relationship between sexual orientation and genetic factors, there is no specific gene that determines sexual orientation (Ganna, et. al. Science [5]). The author used a pairing model that includes this information and the more comprehensible LGBTQ+ persons whose body and mind do not match, where under realistic parameter conditions, a few percent of LGBTQ+ children are always born at a steady rate. The model was derived as follows. Non-LGBTQ+ (sometimes referred to as heterosexual or cisgender but referred to here as non-LGBTQ+) and LGBTQ+ are represented by MM, MF, FF, and FM. The physical nature is indicated by the capital letter, and the mental nature is indicated by the subscript. Supposing that the human genetic distribution is in a steady state, the male-to-female ratio is 1:1 symmetrical, the probability of non-LGBTQ+ existence (birth) is r, and that of LGBTQ+ birth is 1-r; k, k’, k” are the probabilities of mating preferences and producing a child between the aspects. In other words, k and k’ are the probability that a non-LGBTQ+ person procreates with an LGBTQ+ person of the physically opposite sex.
The relative probability (relative to non-LGBTQ+) k” is the probability that both LGBTQ+ persons procreate. If one child is born with a certain proportion of non-LGBTQ+ and LGBTQ+ children based on the establishment of such pairs, the genetic flow will be as shown in (Figure 3). Here, let r’, α, β, and γ be the probabilities that the child born from each of the four pairs is non-LGBTQ+. The probabilities that they are LGBTQ+ are 1-r’, 1-α, 1-β, and 1-γ, respectively. At this time, the following three-dimensional equation (1) holds true for the proportion r of non-LGBTQ+ people in a steady steady state. (See Appendix Ap2)
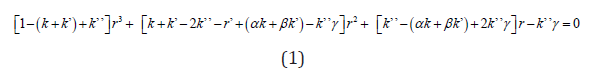
The existence percentage of LGBTQ+ people in society is said to be several to ten percent. In such a model, there exists a steady state solution for r that is a reasonable value as a solution to the cubic equation under reasonable parameters. (Figure 3) shows numerical examples. In addition to LGBTQ+, there are other types of sexual aspects, such as, e.g., “questionable.” Although these are not included in the model, they can be absorbed into 1-k, 1-k’, and 1-k”, so the applicability of the model is sufficient. To determine the solution of this equation, (Figure 4) shows the variation of r with respect to r’ when several γ and k’ are given as parameters. At this time, the pairing rates are fixed at k = k’ = 0.7 because even if they were varied, it would not have a substantial effect on the trends and characteristics of the valid solution.
However, to determine the limit, we also show the solution curve with k’ changed to the maximum limit value of k’=1.0. Similarly, the solution curve with γ = 1.0 (maximum limit) is also shown to determine the limit. The thick lines and × marks are typical curves and typical examples, respectively. Usually, because the non-LGBTQ+ ratio r is larger than that of LGBTQ+ 1- r, the relative number (r2) of pairings between both non-LGBTQ+ people is larger than that between others. Therefore, the non-LGBTQ+ birth rate (r’) from that pair becomes dominant (strongly influences) to the overall non-LGBTQ+ birth rate r, which includes those from pairs including LGBTQ+. For example, the typical example (mark “×”) in (Figure 4) is r’/r = 1.036–1.052.
The research here presented models and mathematical formulas, which are highly objective and can be understood by many people, to accord LGBTQ+ people as a natural phenomenon of the result of the evolutionary process. In this way, we can understand LGBTQ+ sexuality using a comprehensible macromodel theory, thereby eliminating unnecessary intolerance, discrimination, and prejudice against LGBTQ+ people and promote social recognition of LGBTQ+ sexuality as a natural existence. This will lead to the harmonious progress of humanity. This is the purpose of this study. In the artificial life simulation of play/preferences that led to this research, results demonstrated that diversity is important. LGBTQ+ sexual orientation is also a type of diversity where ability conversion or development will function. From the perspective of diversity, as a development of this research, the authors aim to clarify and model these relationships, including the active adoption of side jobs, work-style reforms, flexible discretionary labor systems. These simulations are also expected. An issue that is similar to LGBTQ+ is pedophilia, which is said to affect 5% of the population. Although similar to LGBTQ+, pedophilia is asymmetrical and immoral, and it is necessary to strictly distinguish it. Although LGBTQ+ sexuality or pedophilia are phenotypes that create difficulty in producing offspring, there are a certain number that cannot be ignored.
Although many genotypes are common (including polymorphisms; wild type), some genotypes are due to mutations/biasedness, the balance is disrupted, and the phenotype may be expressed as “heresy.” Because there are many “heretical” genes among the general population, it is expected that using the meta-analysis of public databases, such as LGBTQ+Data.com, will eliminate taboos and tackle several practical social discussions and policies head-on. We hope that this will provide theoretical support. As described above, this study presents two theories that can quantitatively analyze the extent of diversity related to LGBTQ+ sexuality. The areas are as follows: The number of sexes that maximize evolution from a global, long-term perspective is e (Napier’s number = 2.71...). Therefore, it is possible that the two sexes are under pressure to become non-binary, including LGBTQ+. It has also been shown that it is possible to explain why LGBTQ+ people exist in a certain number as a proportion of the population, even though it is difficult for them to produce offspring, leaving the possibility of human evolution open. In short, this article explains the inevitability of LGBT from a scientific and quantitative perspective. Furthermore, this article points out the social problem of boundaries between criminal and moral. These are uniqueness of this article that can hardly be found anywhere else.
The author declares that I have not used Artificial Intelligence (AI) tools in the creation of the article.
The author would like to thank Mr. Kazuma Sekiya, the president of DISCO Corporation, for giving the suggestion to effectively utilize the diversity of employees, which led to this research, and for putting it into practice and showing the remarkable performance of the company. The author would also like to express his deep gratitude to Professor Katsuhiko Chika of Osaka Metropolitan University and Chairman of the Global Urban Business Society for supporting this research and external presentations.
The author declares that there is no conflict of interest.
Derivation of the formulas.
Ap1. Theory of base-e sexes
When x = Nd, we have the evaluation function
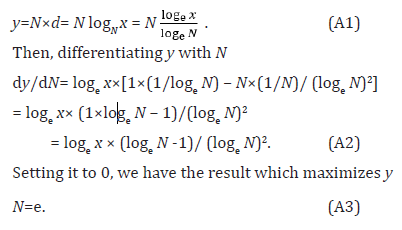
Ap2. Human birth model of sexual aspect
Total of the relative probabilities of mating and making child is from Figure 3,