Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Emin Taner Elmas* and Ismail Kunduracioğlu
Received: April 11, 2025; Published: May 12, 2025
*Corresponding author: Emin Taner Elmas, Assistant professor dr., Vocational School of Higher Education for Technical Sciences, Division of Motor Vehicles and Transportation Technologies, Department of Automotive Technology, Iğdir University, Turkey & Graduate School of Natural and Applied Sciences - Major Science Department of Bioengineering and Bio-Sciences, Iğdir University, Turkey
DOI: 10.26717/BJSTR.2025.61.009659
This article gives introductory information about the “Conservation Laws and the Main Physical Parameters for Advanced Biomechanics”. The study has been realized within the scope of a Ph.D. lesson which is lectured by Asst. Prof. Dr. Emin Taner Elmas. The name of this Ph.D. lesson is “Medical Engineering and Advanced Biomechanics” and taught at the Major Science Department of Bioengineering and Bio-Sciences at Iğdır University, Turkey. İsmail KUNDURACIOĞLU is a Ph.D. student and he is one of the students taking this course. This article has been prepared within the scope of this Ph.D. lecture, as a part of one of his (İsmail KUNDURACIOĞLU) homework assignment tasks which was prepared using the summary translation of Reference [1]: Book Part 1. [1-67].
Keywords: Conservation Laws; Conservation of Mass; Conservation of Momentum; Conservation of Energy; Bones and Muscles; Blood Vessels; Pressure; Tension; Physical Stress; Advanced Biomechanics; Biomechanics; Comparative Biomechanics; Anatomy; Physiology; Thermodynamics; Energy Transfer; Fluid Mechanics; Heat Transfer; Mathematics; Medical Technique; Medical Engineering; Medicine; Biomechanical Analysis; Bioengineering, Health Science
Field Preparation
This will be the first of two sections that will present terminological, conceptual, and logical tools from the physical sciences for analyzing biological situations. These tools assume familiarity with topics typically covered in basic mathematics and physics courses, but include topics that most biology students rarely encounter or often overlook in their courses. The information in this article is essential to biomechanical analysis because the simplifying assumptions in these courses, such as solid bodies, frictionless fluids, and resistance less motion, prevent us from understanding the subtleties of biomechanical functioning in nature. Therefore, the abstract concepts presented provide a more comprehensive understanding in biological analysis. [1-67].
Conservation Laws
Some of the most elegant and powerful statements in physics are the conservation laws. Each law states that in any process occurring in a neatly isolated system, some things remain the same. That is, some quantities always retain the same total value, amidst changes of state of matter, chemical arrangements, speeds, shapes, and other complex transformations. Many such laws will be of particular use to us. [1]
Conservation of Mass
Conservation of mass has an important application in fluid mechanics as the “principle of continuity”. For example, when a functionally incompressible liquid, such as water, flows through a rigid pipe, the mass and volume remain proportional; therefore, the principle applies to both quantities. The rate of mass flow through any point in the pipe must be equal to the rate of mass flow through any other point in the pipe, because the liquid is incompressible and the pipe is rigid. This is a simplified model, but a good approximation. For example, it is a consequence of the principle of continuity that water exits a pipe at a higher speed at the narrower end. [1] This principle also works in a simple form for gases; when flow velocities are lower than those commonly encountered in living systems, gases are not compressed by the flow. Therefore, the mass and volume relationship is not affected by velocity. However, when compression is significant, the density is no longer constant and the application of the principle becomes more complicated. [1] Very small blood vessels, such as capillaries in the body and tracheoles in the respiratory tract, have a much slower flow rate than the aorta or bronchi (Figure 1). Therefore, their total cross-sectional area must exceed the area of the aorta and bronchi. Using this principle, we can approximate how many capillaries are open and functional in a person at rest. [1]
Conservation of Momentum
Momentum (mass m Understanding the concept of velocity times v) allows us to state a powerful new conservation law. While mass is a scalar quantity, velocity is a vector quantity; hence, momentum is in the direction of the velocity. Therefore, when an object moves in a certain direction, it creates positive momentum, while when it moves in the opposite direction, it creates negative momentum. For example, when two pieces of clay of equal mass collide with equal and opposite velocities, the combined masses remain at rest and the sum of their momentums is zero. To better understand this conservation law, consider a hose and a nozzle. When the nozzle is narrowed, the hose is seen to be pushed backwards. Here, while the speed of the water coming out of the hose increases, the amount of water flowing in a given time period remains the same (the principle of continuity prevents this). As the water leaves the hose, its momentum increases and pushes the hose back. If you do not hold the hose, it will move backwards; otherwise, this momentum is transferred to the ground through your feet. [1] This principle is also seen in artillery fire or rocket recoil; the backward thrust of gas causes the devices to move forward. Similarly, a fish moves forward by imparting backward momentum to the water. When water hits a stationary object, its speed decreases and its momentum decreases, creating a backward force (drag) on the object. By measuring the decrease in momentum of the water, you can calculate the drag of the object without directly touching it; this is especially useful with organisms that are distressed or immobile. [1]
Conservation of Energy
The law of conservation of energy is known as the “first law of thermodynamics” and is one of the most well-known conservation laws. However, it is less useful for biomechanical problems than the law of conservation of momentum; it is only considered when non-purely mechanical issues such as heat, metabolism, or storage of potential work come into play. The important difference between the laws of conservation of momentum and energy is that both deal with mass (m) and velocity (v), but momentum is a vector quantity that is directional. Energy, on the other hand, becomes non-directional when the velocity is squared. For example, when two equal masses collide and stick, kinetic energy is destroyed but conserved and mostly converted to heat. [1]
Unprotected Quantities
Mass, momentum, and energy form the basis of conservation laws. However, quantities such as force are not conserved; you can turn a small force into a large force with levers or pulleys. Power is also not conserved in the short term. For example, a flea can reach great speeds with its short legs by storing energy and transferring it to an elastic cushion, which can release a very high force when released rapidly. [57,58]
Biological Significance of Stress
In the following sections, we will encounter several variants, but one must be considered first, as it appears in many different contexts. Although it may seem simple at first glance, the references made in everyday speech are often misleading. For example, if you press a knife against a carrot with a force of 10 newtons on its wide surface, the carrot remains firm; but if you apply the same force with the sharp edge, the carrot is cut. Often, it is not the force that should be considered, but the physical concept of “stress”, which is the result of dividing the force by the area to which it is applied. Expressions such as strength or durability often refer to stress. Durability actually refers to a certain level of stress, such as the stress at break. This highlights the importance of stress. The most common symbol for stress is the Greek letter sigma (σ), which is expressed in the SI unit of newtons per square metre, or Pascal (Pa). Since the Pascal unit represents such a small quantity, the units meganewton or megapascal are more commonly used. [1] Stress inevitably creates deformation; stress is how much force you apply to something, and deformation is how much the thing changes shape as a result of that force. In the real world, nothing can reach perfect rigidity, so when a stress is applied, a deformation always occurs. This inevitability allows strain gauges to be used to measure stress by calibrating them. We need to distinguish between types of stress (Figure 2). [1]
Tensile Stress: Tensile stress is a force exerted on a unit cross-sectional area and occurs when two ends of an object are tried to be pulled apart. For example, when you pull on the ends of a string, a piece of candy, or a metal or wooden beam, tensile stress occurs whether or not the material stretches. The area considered for converting force into stress is the area perpendicular to the force. This is the cross-sectional area of the string, candy, or beam. [1]
Compressive Stress: Compressive stress is the opposite of tensile stress, in which the object is compressed. Pressing against a wall, stepping on a full beer can, or closing the nozzle of a bicycle pump and pressing down on the handle all apply compressive stress to liquids, solids, or gases. Again, the area considered is the area perpendicular to the force. The symbol for both tensile and compressive stress is “σ”. [1]
Shear Stress: Shear stress is quite different from the first two types of stress. In this stress, forces are applied to an object in opposite but non-coincident directions. When such a pair of forces is applied, the object usually tends to rotate; but here we assume that the object is not rotating and therefore must change shape. Shear stress is most noticeable in a soft material—for example, a wet sponge, dough, or gel. Shear stress results in movement in the direction of the applied force for a certain distance. The area considered here is in a horizontal plane, not vertically as in tensile and compressive stresses. The appropriate symbol for shear stress is usually given as “τ”. [1]
Other Structural Stresses
When forces are applied to objects with certain shapes, two additional types of stresses are created: bending (flexural) and torsional (torsional) stresses. These structural stresses can be thought of as combinations of the three basic “material” stresses. For example, if you bend an object, you stretch one side and compress the other, creating shear stress in the middle. When you twist an object (for example, a wet towel), you stretch the outside and compress the inside, creating shear between concentric cylindrical layers in the center. [1]
Stresses on Organisms
Bones and Muscles: The force that a muscle can exert depends on its cross-sectional area. For example, ordinary striated muscle can exert a maximum tensile stress of about 0.1 to 0.5 megapascals. This means that a muscle with a cross-sectional area of 10 square centimeters can exert a force of 100 to 500 newtons (about 20 to 100 pounds). A bone can withstand about 200 megapascals of longitudinal compression. This suggests that bones are more durable than muscles. [59]
Compensatory Growth in Trees: Trees similarly respond to increased loads by producing “reaction wood.” This indicates that trees are sensing stress or strain. If a supported tree’s growth is inhibited, it will not be able to adequately strengthen itself and will not be able to stand safely when the supports are removed. [60] Sizing of Blood Vessels: Pressure in closed vessels creates tensile stress on their walls. When the blood flow rate increases, shear stress occurs on the vessel walls and the vessel feels this stress and grows or shrinks. This principle is known as “Murray’s Law”, developed by Cecil Murray, and predicts that the vessel diameter should be directly proportional to the flow rate. [1]
Importance of Size
There is a huge difference in scale between the size of atoms and molecules and the size of life forms. For example, the number of molecules in a cell is equal to the number of cells in a cat compared to the number of cells in a cat. As Schrödinger noted in his 1944 work “What Is Life?”, well-ordered structures can only be formed by the misbehavior of individual atoms when there are enough atoms. [61] Living organisms range in size from the smallest bacteria, about 0.3 micrometers long (about one hundred thousandth of an inch), to whales, about 30 meters (100 feet) long. This represents a difference of about 100,000,000 times in magnitude. The book “Powers of Ten” by Morrison and Morrison (1982) provides an excellent introduction to the cosmic subject of size. Size plays a large role in comparative biomechanics because it covers the entire size scale of organisms. [62]
We humans are relatively large beings, about three or four feet tall. While there is only a small amount of size difference between us and the largest living beings, there are six to seven orders of magnitude between us and the smallest. A “typical” organism is usually between one millimeter and one centimeter in size. Size largely determines the nature of the organism’s physical environment and the phenomena that directly affect its life. [1] To better understand the relationship between size and reality, we can consider airborne animals. These creatures are denser than the environment around them and can fall when dropped from a height. We can divide organisms into four categories based on the consequences of their fall:
Category One: Animals weighing more than about 100 kilograms (220 pounds). These animals can be injured if they fall from a distance shorter than their own height. For example, this is the case for cows and horses. [1]
Category Two: Animals weighing between about 100 kilograms and 100 grams (4 ounces). These animals can be injured by a fall, but the distance of the fall must be greater than the animal’s height. For example, dogs should avoid cliffs, and cats should descend trees with caution. [1]
Category Three: Creatures weighing 100 grams to 100 milligrams. Falling creatures of this size are usually harmless; the threat is usually from ground-level predators. For example, two mice that fell from a roof were briefly stunned but unharmed. [1]
Category Four: The smallest airborne organisms. The fall of these organisms is of uncertain statistical significance; they may remain suspended in the air or fall slowly. [1] Although gravity is the same everywhere on Earth, the practical effects of this force vary depending on the size of the organism. Consequently, size is no small factor in the design of organisms. Dimensional variation in living things is very wide. Comparing a spheroidal bacterium to a large whale is a good example to illustrate this point. The size of organisms plays an important role in evolutionary and practical “fitness”; nature has determined the sizes according to the unique characteristics of each organism (Table 1). [1] The relative decrease in surface area as the body grows triggers a certain response in the evolutionary process. This response does not involve a violation of geometry, but rather an escape from the assumption of isometry; it involves a great proliferation of additional surfaces that are often hidden in larger organisms. The relationship between a whale and a bacterium to geometric isometry is much more than what appears on the surface. We can illustrate this with some examples: Trees appear much less round than whales or bacteria because they have a very pronounced leaf surface. For example, an orange tree with 2,000 leaves would have an outer surface of 200 square metres, while the inner surface for gas exchange is 30 times greater, i.e. 6,000 square metres (0.6 hectares).
Plants absorb water and minerals from the soil; this process depends on adequate surface area. A square metre of lawn planted with Kentucky bluegrass has 10,000,000,000 root hairs and a total surface area of 350 square metres; twice the floor area of my entire house. [1] The lungs are our functional interface with the atmosphere. The capacity of a pair of lungs is about 6 liters, but when this volume is divided by 30,000,000 alveoli, the total surface area varies between 50 and 100 square meters, equivalent to the floor area of a large classroom. [1] The entire digestive system is considered to be outside the body. Absorption of nutrients into the blood and cells occurs primarily through the walls of the small intestine. Each individual has a small intestine that is approximately 7 meters long and has projections such as villi and microvilli on it; the total surface area of these structures reaches 2000 square meters (0.5 acres). [1] Even inside the organism, the places of exchange processes are the areas where the surface is increased. Our muscles exchange various substances such as oxygen and carbon dioxide with the blood circulation; this process takes place through the walls of capillaries, whose total surface area is about 6000 square meters, which is the same as the total internal surface area of the leaves of an orange tree. [1] As a result, as biological systems (organisms or internal components of organisms) grow, there is an increasing tendency towards functional sphericity. This arrangement can be recognized even at the cellular level; many metabolic machines operate on surfaces, and cells are filled with internal membrane surfaces. In cases where surfaces maintain absolute (not relative) internal spacing, the surface area of the system remains proportional to its volume. Growth is usually allometric, with parts increasing disproportionately. Thus, shape becomes a function of size. [1]
Pressure Stress and Radius of Curvature
There is a size-dependent relationship that is biologically important, related to the tension created by the pressure difference on the curved walls between cylindrical and spherical structures. Here we are talking about thin-walled biological balloons, where a tensioned wall surrounds a pressurized volume. For example, when you slowly inflate and deflate a spherical balloon, you monitor its internal pressure. As the balloon grows, the surface membrane becomes more taut, and you might think that the internal pressure would also increase. However, the manometer tells a different story; the pressure is much more constant than proportional to the volume. A slightly higher pressure is measured at the point of zero inflation, and a slightly higher pressure is measured if the balloon is tested just before it bursts. You will notice that you experience this pressure behavior every time you inflate the balloon; it is initially difficult, then as it grows, it does not become more difficult to expand, and there is a feeling of fear at the moment of bursting. The same pressure-volume behavior is seen in urinary bladders and other biological bags. In the medical literature, concepts such as “reflex softening” have been introduced to explain this pressure constancy.
Why shouldn’t pressure and tension remain simply proportional? The dimensions of pressure and tension are key here; pressure (like stress) is expressed as force per unit area, while tension is expressed as force per unit length. When you stretch a thin sheet of rubber, you need to apply more force to stretch a given distance as the width of the sheet increases. However, when you press on a flexible surface, you need to apply more force to compress a given distance as the surface area increases. To convert stress to pressure, that is, to determine the internal pressure created by a wall stress, we need to divide the stress by the length. The specific formula depends on whether we are dealing with cylinders or spheres; cylinders bend in only one direction, while spheres bend in two directions. [1] the pressure difference between the inside and outside as Δp, the wall tension as T, and the radius (or “radius of curvature”) of the object as r, our formulas are:
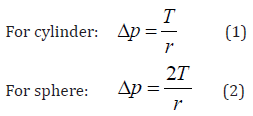
This relation between pressure, tension, and radius for curved structures has been called “Laplace’s Law”, at least by biologists, after the French mathematician and astronomer Pierre Simon Laplace. In fact, Thomas Young may have been the first to note this, and “Laplace’s law” is often confused in mathematics with the “Laplace transform” and “Laplace’s equation”. [1] This rule has a simple origin. Consider the force balance on a cylinder that is split in half lengthwise. The halves are pushed apart by the pressure Δp on the effective area in both directions. This creates an effective area equal to the area of the split surface; this area is calculated by the length (l) times twice the radius (2r), so the external force is 2Δpr. However, the force holding the cylinder together (Figure 3a) is the tension force at the top and bottom edges of the cut; this force is 2T. When we equate and rearrange these two forces, Equation (1) emerges. For a split sphere (as shown in Figure 3b), 𝜋 T 2 Δp will push outward, while 2 𝜋 rT will hold the halves together. Equation (2) emerges by rearranging the forces. [1]
Results – Cylinders
The effects and applications of cylinders are both profound and mundane. For example, the thin tires of a racing bicycle are usually inflated to about 700 kilopascals (seven atmospheres, or 100 psi), while the tires of a car only take about 200 kilopascals (two atmospheres, or 30 psi). However, car tires must be thicker because of the stresses on their walls. [1] A few years ago, I built a flow tank to expose organisms and models to water currents. Water pumped from the top channel had to return through a similar channel several feet downstream; the hydrostatic pressure at the bottom was therefore about 10 kilopascals (1.5 psi). I noticed that the cost of the pipe increased with the square of the diameter. Larger pipes must increase not only with their circumference but also with their wall thickness to withstand the same pressure; Laplace’s law requires that the thickness increase in proportion to the diameter. With these economics in mind, I built my first large flow tank with a return channel made of cheap plywood instead of expensive plastic pipe. But this choice made me realize why the pipes had to be round; square pipes have straight walls, and those walls have an infinitely large radius of curvature. So any internal pressure, say 10 kilopascals, would create infinite stress on those walls.
In reality, the walls bulged a little and put a lot of strain on the corner joints, leading to constant leaks. After this experience, I realized that I needed to invest in cylindrical pipes for the return ducts. [1] The very thin walls (about 20 micrometers) of the xylem elements (about 0.1 millimeters in diameter) that carry water in the trunk of pine trees can also withstand an internal pressure of about 2 megapascals, or 20 atmospheres. In this case, both the pressure and the wall stress would be negative; failure would be by buckling failure rather than bursting. However, the relationship between pressure and stress is valid. Our perception of high pressure needs to be adjusted according to the size of the system; failure is due to tension. [1] Blood vessels are cylindrical in structure and can withstand internal pressure. Furthermore, our capillaries have a pressure that is about one-third the internal pressure of the aorta (13 kilopascals instead of 4 kilopascals); they carry this pressure through walls that are only one cell thick. The tension in the walls is reduced not by a factor of 4/13, but by a factor of 10,000. This can be checked by calculating with the radii of the aorta (13 millimeters) and the capillaries (4 micrometers). As the wall thickness decreases from 2 millimeters to 1 micrometer, the tensile stress (calculated by dividing the stress by the wall thickness) is reduced by a factor of 10,000/2000, or only five-fold. In short, the stresses on the aorta and the capillary walls are quite similar, even though their thicknesses are different. [1] It is important to note the stress in the cylinder walls; here we are talking about hoop stress. The stress in any wall is equal to the stress divided by the wall thickness. Therefore, we can rewrite the equation in terms of stress. The form of equation (3) for the hoop stress in a thin-walled cylinder is obtained:
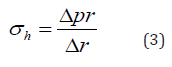
The internal pressure of a cylinder produces a longitudinal stress. The longitudinal stress results from an equilibrium and is analogous to the derivation of Laplace’s law for a sphere. This pressure tends to push out the circular ends of the cylinder. The equation in the texts (Equation 4) relates the wall stress of the cylinder or the stress in the sphere. [1]
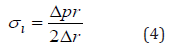
It is noteworthy that the hoop stress (circumferential stress) is exactly twice the longitudinal stress. If you burst a cylindrical balloon, the rupture will produce a longitudinal gash. This indicates that the balloon has burst radically, i.e. not at its ends. Blood vessels are more supported against circumferential failure than longitudinal failure. If a cylinder is wrapped with helically (diagonally) reinforced fibres, these fibres need to be wrapped slightly more circumferentially. If the fibre angle is slightly more than 45°, the stresses can be accommodated equally. [1]
Force and Pressure Properties of Spheres
A sphere with two-way curvature is automatically stiffer and more rigid than a cylinder with the same radius of curvature. For example, a given pressure will be half as effective in producing tension in a spherical vessel as it is in a cylindrical vessel. This explains why a cylindrical vessel can have hemispherical ends, and the ends can have a larger radius of curvature (flatter) than the side walls. [1] Laplace’s law has an additional consequence for spheres. In an experiment in which two spherical balloons are pressurized together by a Y-tube, an interesting situation occurs when one balloon is first completely inflated while the other begins to fill. This contradicts the fact that there is no difference in pressure between the two balloons, one soft and the other inflated. If the inflated balloon is compressed sufficiently, the soft balloon may begin to fill; at a certain point the compression becomes unnecessary and the inflated balloon completes its process, becoming completely deflated and almost empty. In this case, the pressure produces more stress on the surfaces of greater curvature, while the stress on the walls of the separate containers is less. [1]
Biological Applications
Each human being has two lungs, like subdivided balloons inflated through a tracheal Y-tube. The lungs are inflated by reducing the pressure outside them (by the diaphragm descending and the ribs expanding). The two lungs are in separate compartments, separated by a solid wall called the mediastinum. This allows one lung to collapse without life-threatening consequences, such as a punctured lung. The presence of two balloons in a glass jar has been a hoax for biology students: either the balloons are not large enough, or teachers explain their failure to inflate by supposed differences. [1]
Alveolar Expansion
The alveoli face a similar problem; why does one alveolus not burst before the others swell? The external pressure difference across the alveolar walls works against two sources of resistance: tissue elasticity and the surface tension of the inner water layer. Surface tension prevents additional air-water surface from forming as the alveoli expand. However, a surfactant secreted by the cells in the alveolar walls reduces the surface tension. This substance acts as the alveoli expand, increasing surface tension; thus opposing expansion as the alveolus swells. “Hyaline membrane disease” is associated with insufficient production of surfactant. [1]
Small Spheres and Pressure
Laplace’s law also explains how thin-walled small sapphires can withstand large internal pressures; in plant cells the internal pressures are often over a million pascals. Carpita (1985) studied the pressures that various thick-walled cells can withstand and found that these pressures correspond to a narrow range of nuclear strengths. [63]
Great Dome Structures
The basic principle of Laplace’s law also applies to large domes. Here the pressure analog is gravity. The loading forces are inward, and the dome must take on negative tension. A larger or flatter dome will produce greater compression under the same weight and therefore must be reinforced. However, this reinforcement may result in an increase in weight at the same rate, which may be undesirable for architectural applications. Natural domes also exist in nature, such as pumpkins, turtles and human heads. [1-67]
In this chapter, we have examined in detail how the physical and mathematical tools that will form the basis of biomechanical analysis play a critical role in understanding biological systems. The fundamental principles of physical sciences – conservation laws, the principle of continuity, conservation of momentum and energy – are indispensable tools in the study of biological phenomena and in explaining the complex workings of nature. These tools provide the opportunity to go beyond simplifying assumptions and to interpret the multi-layered and dynamic processes observed in real life in a more comprehensive way. [1] In particular, how fundamental principles such as the mass-volume relationship apply to liquid and gas systems is of vital importance in the study of biological flows (e.g. blood vessels, respiratory tracts, and other fluid systems). The explanations provided by the principle of continuity for the changes in flow rate that occur with constricted and expanded pipe cross-sections shed light on the understanding of the adaptation processes and functioning of biological systems. Similarly, the conservation of momentum, the interactions of moving objects, and the reflections of these interactions in biological models play a critical role in the analysis of the mechanisms of movement and balance of organisms. [1] The conservation laws discussed in this chapter are not limited to simple mathematical formulas, but have also been used to explain how real-world systems operate, such as the wall tension of blood vessels or the expansion of lung alveoli. Laplace’s law provides important information about the durability and functionality of biological structures by revealing the relationship between internal pressure and wall tension in both cylindrical and spherical structures. These principles also reveal how pressure and tension differ at the organismal scale, and how size is an evolutionary and functional determinant. [1]
In addition, the huge differences between the sizes of biological systems play a decisive role not only in the structural arrangements of organisms but also in achieving functional sphericity. The sizes of organisms are not just geometrical features, but also reflect how the basic principles of life, matter, energy and forces, are distributed and which interactions dominate at which scales. This is valid both at the micro level (intracellular processes and molecular interactions) and at the macro level (organ, system and organism levels). [1] In conclusion, the theoretical tools and principles presented in this section provide a solid foundation for us to grasp the rich and multidimensional structure of biomechanical analyses. Terminological, conceptual and mathematical models provided by physical sciences serve as powerful guides in revealing the subtleties of biological systems. This approach shows that biological events cannot be explained with simple assumptions, but rather require detailed analysis of the complex structure and dynamic processes of nature. Thus, both researchers and practitioners can perform a more holistic and in-depth analysis of biological systems by utilizing these principles, and make more accurate and comprehensive interpretations of the functioning of nature [1-67].


