Comparing of Using Different Systems of Kinetic Equations for Numerical Simulation of Deflagration Initiation in Hydrogen-Air Mixtures Flows Volume 61- Issue 2

Martyushov S N*

• Moscow Aviation Institute, National Research University, Russia

Received: March 28, 2025; Published: April 10, 2025

*Corresponding author: Martyushov S N, Moscow Aviation Institute - National Research University, Moscow, Russia

DOI: 10.26717/BJSTR.2025.61.009585

Abstract PDF

Abbreviations: ODE: Ordinary Differential Equations

Main preference of hydrogen as a fuel is detonation fuel cycle which is more energetic preferable in comparing with ordinary fuel cycle [1]. In connection with this preference problem of hydrogen detonation engine constructing is extreme actual. Perspective results are projects of pulsing detonation engine [1] and spin detonation engine [2,3]. Nowadays investigations in this field are provided mainly by mathematical modelling methods. Essential part of investigations is developing and improving of mathematical methods for numerical simulation of deflagration initiation and transition from deflagration to stable detonation in hydrogen-air gas mixes flows. From the kinetic point of vie process of transition to detonation can be treated as transition from slowly deflagration to branching chain reaction in hydrogen- air mix. Different authors [4-7] used different systems of reactions for numerical simulation of hydrogen-air mixes deflagration. In this paper attempt was made to compare results of using some of these different systems. Coefficients for all reactions, used in this paper where taken from [8].

Process of deflagration appearance in hydrogen-air mixes can be treated as transition from slow chemical reactions to fast branching chain reactions. Theory of branching chain reactions was developed by Semenov [4]. Equations of chemical reactions can be presented as follows

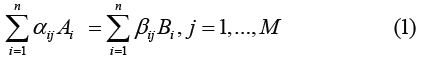
where M, n–number of reactions and components of the mix, α_ij , β_ij - coefficients of direct and inverse reactions. Arrhenius low is predicted for calculating of speeds of changing of mix components concentration c_i

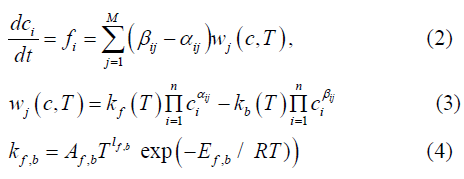
The algorithms for numerical solving of system [2-4] consist of solving fool system of stiff ODE (ordinary differential equations) on the basis of numerical Gear method. Different authors [4-7] used different systems of reactions for numerical simulation of hydrogen-air mixes deflagration. In this paper we try to compare results of using some of these systems. The first system of reaction for hydrogen-air gas mix of 9 component: Н₂, О₂, Н, О, Н₂О, ОН, НО₂, Н₂О₂, N₂ is the most widespread. The next 9 reactions where choose: Results of numerical decision (for small closed finite volume without gas dynamics effects) of stiff ODE system [2-4] on the basis of Gear method with system of reaction from Table 1 are shown on the Figure 1. Initial meanings of components H₂ =0.2 of molar amounts of mix, O₂ =0.1 of molar amounts of mix, N₂ =0.7 of molar amounts of mix, initial concentration of H₂ O =0., final meanings of H₂ O 0,2 of molar amounts of mix. During the calculation time changes from 0 to 12 sec. Calculation began with temperature T=3.3Tatm, and it changes during calculation in connection with heat effect of chemical reactions. From this example and the next ones can be seen that appearance of significant amount of radical H₂ O₂ in gas mix lead to fast speed of changing for main components (H₂, O₂ and H₂ O), that demonstrate deflagration initiation. The second system of reactions (situated in Table 2) was system of 13 reactions for the same components Н₂, О₂, Н, О, Н₂О, ОН, Н О₂, Н₂О₂, N₂: Results of numerical decision of stiff ODE system [2-4] on the basis of Gear method with system of reaction from Table 2 are shown on the Figure 2. Initial meanings of components H₂ =0.2 of molar amounts of mix, O2 =0.1 of molar amounts of mix, N₂ =0.7 of molar amounts of mix, initial concentration of H₂ O =0., final meanings of H₂ O 0,2 of molar amounts of mix. During the calculation time change from 0 to 9 sec. Calculation began with initial temperature T=3.25Tatm. The third system of reactions (situated in Table 3) was system of 28 reactions-with one additional component O3: Results of numerical decision of stiff system of ODE [2-4] on the basis of Gear method with system of reaction from Table 3 are shown on the Figure 3. Initial meanings of components H₂ =0.2 of molar amounts of mix, O₂ =0.1 of molar amounts of mix, N2 =0.7 of molar amounts of mix, initial concentration of H₂ O =0., final meanings of H2 O 0,2 of molar amounts of mix. During the calculation time change from 0 to 9 sec. Calculation began with temperature T=3.1Tatm, and it changes during calculation in connection with heat effect of chemical reactions.

Table 1: CT Exam Protocol.

Table 2: The first system of chemical reactions.

Table 3: The third system of chemical reactions.

Figure 1

Figure 2

Figure 3

In this paragraph we compare using of systems of reactions from Table 2 and Table 3 for numerical simulation of deflagration appearance in hydrogen – air gas mixtures flows. Numerical simulations of deflagration appearance in hydrogen – air gas mixtures flows with using system of reactions from Table 1 can be found in, for example, in [4-7] and previous papers of author [9]. The system of the equations of ideal gas and the kinetic equations in the integral form for two dimensional flows with source term which are velocities of changing gas mix components (2) can be presented as follows:

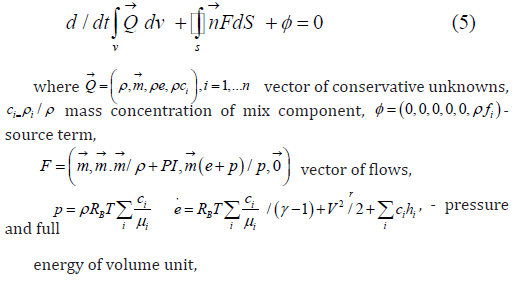
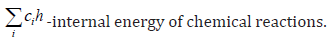
Numerical simulation where provided for test problem of deflagration initiation from spreading shock wave of intensity of Msh and initiating of deflagration front in isolated cylinder for hydrogen-air gas mixes. Numerical algorithm [9] was developed on the basis of pure upwind variant of difference scheme Chakravarthy - Osher [10] second order of accuracy for time and third order accuracy for space. Aim of providing calculation was simulation of initial stage of deflagration. The first example consist of numerical simulation deflagrarion initiation in hydrogen – air gas mixtures flow behind shock wave intensity Msh=3.5 (calculations was provided with stable shock wave and appropriate velocity of flow before shock) for system of chemical reactions from Table 2 (Figure 4). The second example just the same consist of numerical simulation deflagrarion initiation in hydrogen – air gas mixtures flow behind shock wave intensity Msh=3.5 (calculations was provided with stable shock wave and appropriate velocity of flow before shock) for system of chemical reactions from Table 3 (Figure 5).

Figure 4

Figure 5

Three test variants of numerical solution of system of stiff ODE [2- 4] for system of reactions from Table 1, Table 2 (9 components, 9 and 13 reactions) and Table 3 (10 components, including O3 and 28 reactions) where provided. Proposal was used that process of deflagration initiation realized in one small closed finite volume without gas dynamic effects. For testing possibility of using system reactions from Table 2 and system reactions from Table 3 in gas dynamic numerical simulation of flows with hydrogen-air deflagration two variants for one gas dynamic problem was calculated. Gas dynamic problem consist of deflagration initiation behind stable shock wave of intensity Msh 3.5 in cylinder. (Possibility of using system reactions from Table 1 was shown previously in numerous calculations of different authors, see [4-7] and author himself [9]).

Results of provided calculations demonstrate possibility of using system reactions from Table 2 and system reactions from Table 3 in gas dynamic numerical simulation of hydrogen-air deflagration. This results didn’t show preferences of using system reactions from Table 2 and Table 3 before using system reactions from Table 1. Nevertheless, using systems reactions from Table 2 and Table 3 provide additional possibilities for solving other problems in numerical simulations of gas dynamics flows with deflagration.

1. Taki C, Fujiwara TF (1978) Numerical analysis of two-dimensional non steady detonations. AIAA Journal 16(1): 73.
2. Zhdan SA, Bykovskii FA, Vedernikov FF (2007) Mathematical modeling of a rotating detonation wave in a hydrogen-oxygen mixture. Combustion Explosion and Shock Waves 43: 449-459.
3. Frolov SM, Aksenov VS, Shamshin IO (2007) Shock wave and detonation propagation trough U-bend tube. Proceedings of the Combustion Institute 31(2): 2421-2428.
4. Semenov NN (1967) Uspehy Himii 36: 3.
5. Denisov ET, Sarkisov OM, Lihtenshtein GI (2000) Chemikal Kinetic (Moscow), Himiya, pp.568.
6. Liberman MA (2008) Introduction to Physics and Chemistry of Combustion, Springer-Verlag, Berlin-Heudelberg,
7. Galburt VA, Ivanov MF, Mineev VN, Fortov VE Funtikov AI (2002) Action of Hydrogen Explosion on Reactor Hall Safety Containment. J of Mathematical Modelling 14(1): 73-86.
8. Ibragimova L B, Smechov G D, Shatalov O P (2003) Recommended Rate Constants of Chemical reactions in an H₂-O₂ Gas Mixture with Electronically Excited Species O₂, O, OH Involved. Institute of Mechanics of Lomonosov Moscow State University 11.
9. Martyushov SN (2021) Numerical simulation of deflagration in hydrogen-air gas mixes. J of Physics: Conference Series 2124.
10. Chakravarthy SR, Osher S (1985) Appl Math. 22(1): 57.