Complex Network Analysis and Implementation to Wildlife Corridor Using Machine Intelligence Volume 59- Issue 3

Saurabh Shanu*

• School of Computer Science, UPES, India

Received: November 04, 2024; Published: November 15, 2024

*Corresponding author: Saurabh Shanu, School of Computer Science, UPES, Dehradun 248007, Uttarakhand, India

DOI: 10.26717/BJSTR.2024.59.009311

Abstract PDF

The work of designing wildlife corridors for any focal species is quite complex and scientific (Hilty, et al. [1]). It incorporates a vast array of elements and components. Additionally, the approach does not ensure that the species would disperse in the designated direction; rather, it also depends on a variety of internal factors. These internal factors may be the cause of the focal species’ dispersal from one habitat patch to another (TJB, et al. [2]). The concepts covered in this proposed model centre on the use of computational methods, artificial intelligence and GIS data to gather information of the landscape and identify a set of paths that may serve as possible wildlife corridors in a landscape (Shanu [3]). The first objective is to identify the crucial factors that influence how species disperse. Recently many researchers working in the said area have done ample work using a variety of tools, including literature reviews, field reports, GIS, and remote sensing (Shanu, et al. [4]). Equation (i) shows how a factor set “” is created using “” different detected factors. The opinion proposed in this work assesses the spatial-temporal dependence of the focal species on these parameters for dispersal.

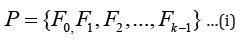
The opinion suggests using machine intelligence’s computational methods to study the interactions amongst the parameters and with the focal species. To do this, a cost surface over the focal landscape is developed using a mathematical framework. A cost matrix “”, representing the cost incurred by the focal species when dispersing across each grid of the landscape matrix, is computed to lay a cost surface on the landscape (Shanu [5]). Equation (ii) shows how the cost of each grid would be calculated depending on how much each factor in the grid is present or absent.

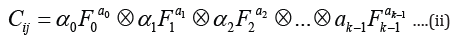
here, α_i indicates the coefficient of factor F_i and a_i represents the order of factor in the equation, where C_ij is the value of the i^th and j^th column of matrix “”. The operation that must be performed within the equation’s constituent parts is denoted by. The equation has to have several different components identified, and the suggested approach makes use of training datasets to do this (Uijlings, et al. [6]). Previous datasets from survey reports, studies of species abundance, studies of species dispersion, GIS datasets, maps from species reports, etc. would be included in these training datasets. After utilising the training dataset to train the model, Algorithm 1 of dependency existence will be used to determine whether or not species dispersion depends on the parameter, and if so, how much.

Algorithm Dependency_Exist ( )
//Input: (i) Set of factors “P”
(ii) training dataset
//Output: Coefficients to evaluate grid cost
Declaration Section
n, i, p, q, count, z as integer
T, L, Pi as double
Procedure Section
n = |P|
For i = 0 to n
If change in Pi changes Cpq //Cpq is the focal grid cost
“Dependency exists”
Else
Func_recheck (Pi)
End If
Result Section:
Dependency coefficients αi found.
Func_recheck (T)
Do while (δT = δL)
δT = δL
δL = Ti+1 - Ti //calculates error
count = count + 1 // no. of iterations
Loop
z = count //z is no. of iterations when error repeats

Output: The constant error gives level of dependency of species dispersal on the parameters

Understanding the degree of dependence provides insight into the coefficients of each parameter in the equation (ii). After obtaining the coefficients, a 2-person game of the prisoner’s dilemma would be modelled to determine the parameter values i F (Wang, et al. [7]). The parameter is designated as the second player, with the focal species as the first. As a result, a score is (will be) determined for each parameter using the game’s payoff matrix. This score is based on how each player strategizes in terms of cooperation or defection (Hertwig [8]). The score matrix for the game is displayed in Table 1. As aforementioned, the model suggests a method for determining the coefficients and values for each factor. Getting the order of each factor in the equation (ii) is a crucial next step. The idea of area occupancy by each element in a focal grid is (will be) used to determine the order. The method used by the proposed model to determine the order of each factor is represented by equation (iii).

Table 1: Payoff Matrix of 2-Person’s Prisoner Dilemma Game.

In order to generate a cost surface over the focal landscape, the suggested approach assesses the significance of each factor (Best [9]). Finding the operator to examine the internal interactions of the parameters is another task the model does. The model suggests using a Recurrent Neural Network (RNN) for the purpose using the training data sets (Sherstinsky [10]). Figure 1 illustrates how the RNN may be utilized and visualized.

Figure 1

1. Hilty J, Worboys GL, Keeley A, Woodley S, Lausche BJ, et al. (2020) Guidelines for conserving connectivity through ecological networks and corridors.
2. TJB, Boyle, Boontawee B (1995) Measuring and monitoring biodiversity in tropical and temperate forests: proceedings of a IUFRO symposium held at Chiang Mai, Thailand August 27^th September 2^nd In: TJB, Boyle, Boontawee B (Eds.).,
3. Shanu S (2023) A decision support system for modelling wildlife corridors in India. Biomedical Journal of Scientific & Technical Research 52(1).
4. Shanu S, Agarwal A (2023) A computational model for determining tiger dispersal and related patterns in a landscape complex. Sustainability 15(11): 8539.
5. Wang Z, Wang L, Szolnoki A, Perc M (2015) Evolutionary games on multilayer networks: a colloquium. The European Physical Journal B 88(5).
6. Uijlings JRR, Van De Sande KEA, Gevers T, Smeulders AWM (2013) Selective search for object recognition. International Journal of Computer Vision 104(2): 154-171.
7. Hertwig R, Hoffrage U (2012) Simple heuristics: the foundations of adaptive social behavior. In Oxford University Press eBooks, p. 3-36.
8. Best J (2018) Anthropogenic stresses on the world’s big rivers. Nature Geoscience 12(1): 7-21.
9. Sherstinsky A (2020) Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Physica D Nonlinear Phenomena 404: 132306.
10. Shanu S, Idiculla J, Qureshi Q, Jhala Y, Aggarwal, et al. (2019) A graph theoretic approach for modelling tiger corridor network in Central India-Eastern Ghats landscape complex, India. Ecological Informatics 50(10): 76-85.