The Chain of KRASG12D Proteins Volume 58- Issue 4

Orchidea Maria Lecian*

• Sapienza University of Rome, Italy

Received: August 07, 2024; Published: September 16, 2024

*Corresponding author: Orchidea Maria Lecian, Sapienza University of Rome, Rome, Italy

DOI: 10.26717/BJSTR.2024.58.009189

Abstract PDF

Some of the Kirsten rat sarcoma viral oncogene homologue (KRAS) are newly analysed. The qualities of the KRASG12D proteins are investigated. In the case of interaction with generic membranes, the corresponding new Hidden Markov-State model is newly defined. The Kolomogorov backward equation and the Kolomogorov forward equations are thereafter considered. The clustering method of the states of the Hiddedn Markov-States Model (HMsM) is one based on the analysis of the root mean-square deviations; the fundamental matrix of the chain is defined. The relevance of the study of the standard deviation in the choice of the representation of the probability matrix is newly studied.

Keywords: Krasg12d; Markov Fundamental Matrix; Markov Probability Matrix; Hidden Markov-States Models; Non-Markov Processes

Abbreviations: HMsM: Hiddedn Markov-States Model; KRAS: Kirsten Rat Sarcoma Viral Oncogene Homologue; HVR: Hyperviable Region; MM: Markov Model; Ras: Rat sarcoma Virus; GDP: Guanosine Di-Phosphate; GTP: Guanosine-5’-Tri-Phosphate

Kirsten rat sarcoma viral oncogene homologue (KRAS) proteins are understood as [1] ’drivers’ in human cancer. The quantification of their qualities have rendered has rendered possible to infer the biological timescales of the processes sampled. The studies can be conducted also at atomic level. The different KRAS proteins are discriminated according to the properties of their hyperviable regions (HVR). The role of KRAS proteins is understood as signal-transducer proteins of the Hyper-Viable Regions (HVR’s) of the pathways. The phenomenon can happen both either as a direct Ras mutation, or according to the proteins in the Ras pathways. The speed of the diffusion of the Ras proteins in membranes are used for signaling the response time in the activation of Raf and in that of PhosphatidylInositol 3-Kinase (PI3K) [2]. The speed of the response time in the activation is relevant for understanding whether all the pathways are ’affected’ in all the coordinates.

In the present paper, the interaction patterns of the KRASG12D proteins are recapitulated; the behaviours are outlined, which allow one to define a new Hidden Markov-State Model in which the clustering methods are based on the analysis of the variances. The oroginating (Markov) chain is newly inspected. The questions about the choice of the representation of the probability matrix for the Markov Model (MM) is here discussed within the obeyance of the Kolomogorov backward equations and to that of the Kolmogorov forward equations according to the experimental data accounting for the variances. The study can be apt for a crisp landscape of the MM, where the states are defined on opportune Borel subset. The analysis is pertinent with the confrontation with possible non-Markov behaviours The present study is relevant within the most recent understanding of new properties of the KRAS12D proteins, as pointed out in [3].

The understanding is proven, that the KRAS interact with the lipidic membranes allosterically [4]; indeed, the binding of the Rat sarcoma virus (Ras) proteins demonstrates a perturbation effect on the conformational ensembles of its ’effectors’ [5]. Inhibitors of KRAsG12G have begun being studied [6]; for this purpose, allatoms molecular dynamics has been attempted to be codified within MarkovState Models (MSM’s): more in detail, stationary probabilities can be derived for the selected MSM. The AMG 510 is an effective selective inhibitor which is apt for interaction with non-small cancer cells. The design of KRAS inhibitors can therefore be pursued; for these purposes the covalent bonds between the compound of the thiol groups from the cystine residue are studied [7]. MSM’s are used to analyse the trajectories from the molecular dynamics. Guanosine di-phosphate (GDP) bounds and Guanosine-5’-tri-phosphate (GTP) bonds of KRAS are studied. The effective MSM is one obtained after clustering: the clustering method apt for describing the dynamics is one which selects the states according to the rootmean-square deviation. The MSM is constructed according to the gathering of the several metastable states after the use of ’defined collective variables’. A transition probability matrix 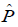is this way constructed, which obeys the forward equation.12 clusters are issued which define the states X_i, i = 1,...,12, which gather the trajectories: probabilities of transition between states are found from the entries of .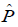

The stationary populations of the states are calculated. It is one of the purposes of the present study to develop the tools to calculate the variation in time of the population(s) of the states; the compatibility with the biological timescales will allow for the comparison with possible properties of non-Markovianity. The differences between the properties of GTP and those of GDP are outlines in the differences between populations of selected states. From [8] and form [9], the difference between ’active’ conformations and ’inactive’ conformations are found in the interaction between the γ-phosphate of the GTP form the Switch 1 region and that of the Switch 2 region. In active conformations, the Switch 1 and the Switch 2 are ’stabilised’. For inactive conformations, the loss of interaction of the γ-phosphate is described. The drug MRTX1133 is known as potential inhibitor of KRASG12D. The structural binding paradigms of MRTX1133 are studied in [10]. MRTX1133 stabilises the sites of the binding after the increase of hydrophobicity, which modifies the movements of Switch 1 and those of Switch 2.

From the results from [6], the states contained in each cluster are selected according to the root mean-square deviation; in the analysis of [4], clusters of states are selected according to the k-mean method [11], according to which a Hidden Markov State Model (HiddMSM) is built. The Kolmogorov backward equation must be imposed for a Markov Model to hold. The fundamental matrix needs to be defined; it is found from the request that the possible transition matrices of the possible chains obey the backward equation

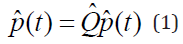
where the p(t) transition matrix is one of the possible transition matrices.

In the present case, the analysis of the variances allows one to define the HiddMSM with a . The main interest in the new HiddMSM is the relevance of the roles of the states X11 and X12; in addition to the calculation of the stationary populations, the passage times from the state X11 to the state X12 can be calculated from the eigenvalues of (i.e. as from [12]). The new HiddMSM is therefore one consisting of the final state where the state X₁₁ and the state X₁₂ are clustered; the resulting state from the Markov landscape is one Borel subset. The construction of this HiddMSM is allowed according to the possibility to build one single state after the clustering of the two previous-mentioned states; this possibility is validated after the control of the variances. The choice of the representation of the probability matrix importantly depends on the entries of the fundamental matrix. The obeyance of the Kolmogorov backward equation is controlled accordingly. The eigenvalues can therefore be calculated. The eigenvalues are once more defined after the control of the variances of the two clustered states.

The behaviour of the KRASG12D are newly analysed with the purpose of isolating the properties which allow one to construct Hidden Markov-States models, whose state are issued according to the analysis of the variances. The forward equation is obeyed by the probability matrix P; the request that the backward equation be obeyed requires the definition of a fundamental matrix of the chain, that, on its turn, allows one to define a host of possible transition matrices , from which the transition matrix apt for the model is scrutinised according to the analysis of the variances. The calculation of the eigenvalues allow one to estimate the Mean Fisrt Passage Times (MFPT’s) and their time evolution. The further perspectives are the study of the changes in population in times of the states Xi within the biological timescales for the dynamics to be validated; the possible chains have to be discussed within the (propagation of the) statistical errors. The compatibility of different timescales within the Markovian features of the model is still an open problem. The new HiddMSM is therefore to be analysed as far as the time evolution of the eigenvalues is concerned. The procedure allows one to reconstruct the time evolution of the errors according to the Markov modellisation chosen, and, in case, on the discretisation scheme adopted, i.e. such as (but not necessarily only) the coarse-graining methods. It is therefore possible to trace back the pathways of the Markov landscape(s) (i.e. the paths on the chosen Borel subset).

1. T Pantsar (2019) The current understanding of KRAS protein structure and dynamics. Comput Struct Biotechnol J 26(18): 189-198.
2. Nussinov, C-J Tsai, H Jang (2019) Oncogenic KRas mobility in the membrane and signaling response. Semin Cancer Biol 54: 109-113.
3. J Kim (2023) Nucleic Acid-Based Approaches to Tackle KRAS Mutant Cancers. Int J Mol Sci 24(23): 16933.
4. C A Lopez, Animesh Agarwal, S Gnanakaran, Andrew G Stephen, Que N Van, et al. (2021) Unveiling the Dynamics of KRAS4b on Lipid Model Membranes. The Journal of Membrane Biology 254(2): 201-216.
5. R Nussinov, C-J Tsai, H Jang (2019) Does RAS activate Raf and PI3K allosterically?. Front Oncol.
6. F Liang, Xianqiang Sun, Jiao Chen, Xuemin Duan, Hu He, et al. (2023) Inhibition mechanism of MRTX1133 on KRASG12D: a molecular dynamics simulation and Markov state model study. 37(3): 157.
7. J Canon, Karen Rex, Christopher Mohr, Keegan Cooke, Dhanashri Bagal, et al. (2019) The clinical KRAS(G12C) inhibitor AMG 510 drives antitumour immunity. Nature 57: 217.
8. F Shima, Shin Muraoka, Min Ye, Mitsugu Araki, Yuichi Ijiri, et al. (2010) Structural basis for conformational dynamics of GTP-bound Ras protein. J Biol Chem 285(29): 22696-22705.
9. M Araki, Fumi Shima, Yoko Yoshikawa, Yuichi Ijiri, Yuka Nagahara, et al. (2011) Solution structure of the state 1 conformer of GTPbound H-Ras protein and distinct dynamic properties between the state 1 and state 2 conformers. J Biol Chem 286(45): 39644-39653.
10. A R Abdul Rashid Issahaku, Johra Khan, Sahar M Aldosari, Clement Agoni, Mithun Rudrapal, et al. (2022) Characterization of the binding of MRTX1133 as an avenue for the discovery of potential KRASG12D inhibitors for cancer therapy. Scientific Reports 12(1): 17796.
11. J A Hartigan, M A Wong (1979) Algorithm AS 136: a K-means clustering algorithm. J R Stat Soc 28: 100-109.
12. O M Lecian (2023) Analytical Expressions of the Markov Chain of K-Ras4B Protein within the Catalytic Environment and a New Markov-State Model. Ig Min Res 1(2): 170.