Non-Markov Processes and Analytical Expressions of Markov Chains of Biomaterials Volume 57- Issue 2

Orchidea Maria Lecian*

• Sapienza University of Rome, Italy

Received: June 19, 2024; Published: June 27, 2024

*Corresponding author: Orchidea Maria Lecian, Sapienza University of Rome, Rome, Italy

DOI: 10.26717/BJSTR.2024.57.008975

Abstract PDF

The Markov chains from which the Markov models of biological macromolecules originate are ana`oytically studied. The aspects of modifications of the Markov chain after numerical approximation are analytically formulated; the comparison between Markovian objects is induced after the individuation of criteria of strong stability and of ergodicity: unassociatedly, the confrontation of Markovian objects and non-Markovian objects is achieved between the framework of the definition of geometrical ergodicity. The perturbation approach is considered: the decays of the correlation functions allow for the Sinai Markov partitions to be set, which constitute the playground on which the Landau–Lifshitz–Gilbert equation is implemented for the construction of the density operator after the collapse of the wavefunction. The applications are scrutinised to the Markov analysis of the Langevin equation for the analytical description of soft matter.

Keywords: Markov Chains; Perturbation Theory of Markov Chains; Ergodic Markov Chains; Strong Stable Markov Chains; Decays of the Correlation Function; Collapse of the Wavefunction; Landau–Lifshitz–Gilbert Equation; Biological Macromolecules; Bio- Chemical Materials

The description of biomaterials in terms of probabilistic interpretation of the phenomenological evidence from the experiential data from biological macro- molecules is presented; in particular, the Markov models are chosen according to their memory-less-ness- properties matched in the data analysis. The long-time-scale dynamics of the biological macromolecules is analysed as ’memory-less’; the time evolution of stochastic biochemical systems is interpreted according to the qualities of the reactants. After the modelisation of the output of the experimental data of an experiment, i.e. one modellising a particular Markov model, the collapse of the wavefunction is interpreted as a measurement postulate. The dynamics of biological macromolecules happens to be fitted after the prescription of the Markov schemes; the time evolution of the macromolecules is exploited according to (computer-based) numerical approximations. The influence of the numerical approximations of the features of the Markov models are analysed in the present work according to the qualities of the Markov chains originating the several Markov Models, which are interpreted within the experimental data: it is understood that numerical approximations might induce modifications in the originating Markov chain, where the modifications can be Markovian or non-Markovian. For these reasons, the qualities of the Markov chains whose descending Markov Models are individuated in the biochemical materials are summarised, and the criteria according to which the perturbed chains are compared with the analytical expressions of the theoretical ones are set.

The Markov approximations are analysed according to their behaviour after the exact time evolution of the density operator; the correspondence with the von Neumann conditions, and the hypothesis that the solutions coincide with the exact density operator are expressed: as far as the obtention of the wished expression of the density operator is concerned, the notion of ’open quantum system’ and that of ’heat bath’ are compared. The von-Neumann equation and the Bloch equation can be juxtaposed: the collapse of the wavefunction is therefore understood as deriving from the Lan- Dau–Lifshitz–Gilbert equation, where the latter can be reconducted to a ’non- linear variant of the von Neumann equation’. The purpose is formulated, that the multiple-pathways techniques be applied to the analysis of ’soft matter’. To these aims, the Markov chains are presented according their technical capability to comprehend the requested tasks. More in details, the features of the Markov chains are analysed, such as ergodicity, strong stability and geometrical ergodicity, for the sake of the Sinai Markov partitions to be applied.

The paper is organised as follows.

• In Section 2, the argumentation for the study of the long-timescale dynamics of biological macromolecules is introduced.
• In Section 3, the focus on the thoeretical understanding of stochastic biochemical systems is motivated.
• In Section 4, the qualities of the dynamics of biological macromolecules which can be theoretised according to the Markov models are evidentiated.
• In Section 4.1, the perturbations of ergodic Markov chains are presented as the schemes according to which the phenomenological evidence is compared with the theoretical framework; in particular, the expansions of perturbation series are explained.
• In Section 5, the perturbations of ergodic Markov chains are studied; associatedly, the notions of strong stability and of ergodicity are reviewed for Markov chains admitting partition with the ’zero’ state, to introduce the criteria for the comparison of Markov chains admitting the same phase space, which are needed for the application of the Sinai Markov partitions.
• In Section 6, geometrically-ergodic Markov chains are complemented with the analysis of the possible non-Markovian modifications of the Markov chains, which can be due to numerical approximation.
• In Section 7, particular clustering algorithms which are used for the definition of some Hidden Markov Models are recalled; as a consequence, the behaviour of the wavefunction can be induced.
• In Section 8, after the stochastic Markov model, both statistical reconstructions and predictions with respect to the unknowns of the equations are accomplished.
• In Section 9, perturbation theory on ergodic Markov chains is performed as far as the aspects of numerical approximations are concerned.
• In Section 10, the ’Markovian-noise’ bath is proposed as a tool of the present investigation; the analysis is aimed at confronting the decay properties of the correlation function, after which the Sinai Markov partitions can be used.
• In Section 11, the Markov approximation of quantum theory of dissipative processes is taken into account for the construction of the density matrix.
• In Section 12, the relations between the von Neumann equations and the Lan- Dau–Lifshitz–Gilbert equation are examined.
• In Section 13, the coarsegrainig methods and the techniques to be applied for the analytical descirption of soft matter are selected.

Long-Time-Scale Dynamics of Biological Macro- Molecules

In [1], the memory-less time-evolution equation is postulated as

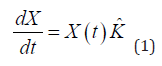
being X the probability of the nth state to be occupied at the time t, and K ≡ {k_ij} the (constant) transition-rate matrix: the k_ij entry corresponds to the transition from i to j. The ’conservation of mass’ laws are expressed as

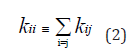
Given the time steps τ, the transition probability matrix (TPM) P ≡ {p_ij} is constructed as with the entries pij corresponding to the transition for i to j. The propagation of the Markov chain is expressed as iterates of the probability matrix.

About Stochastic Biochemical Systems

In [2], the ’chemical equations of motions’ can be calculated.

From the rate equations, the transformation is looked for, which allows one to approximate from the ’continuous domain’ chemical equations of motion to a ’discrete domain of molecular states, with the definitions of the corresponding probabilities and of the appropriate times description. Let qw be the number of all possible combinations of reactant: the molecules are associated with the m-th reaction channel when the system is at a state x, i.e. q(m)(x) is defined as
q(m)(x) = xi, monomolecular reactions; (3a)
q(m)(x) = xi (xi − 1)/2, biomolecular reactions with identical reactants; (3b)
q(m)(x) = xixj, biomolecular reactions with different reactants, (3c)
with i ≥ 1, j ≤ N, i /= j.
Let cm be the probability per unit time for a reaction at the m-the channel, with cm > 0.

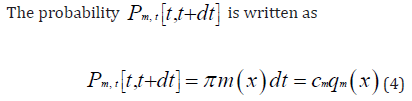
The mean first passage time < t >fp is defined as the average time when a particle reaches the final state for the first time; in particular,

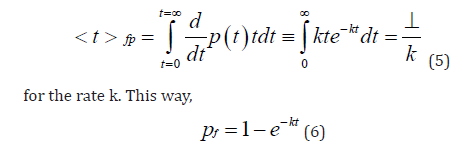
About the Dynamics of Biological Macromolecules

As an example, from [1], the conformational changes of proteins are studied, within the frameworks of protein folding, ligand binding, signal transduction, allostery and enzymatic catalysis.

For a state X, the transition matrix defines the distribution velocity

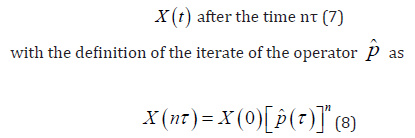
Perturbation Theory of Finite Markov Chains: Markov chains which comprehend one irreducible set of states (sub chain) are studied in [3]. The approach here followed is to impose the variation of the probability matrix. Stationary distributions and fundamental matrices are hypothesised to vary if the probability matrix is perturbed. The method here followed is based on the definition of the fundamental matrix from the given perturbed probability matrix.

Let A be an N -state stationary Markov chain. Let 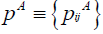be the probability matrix.

Definition a

The ’time-averaged’ probability PA∞ matrix is defined as

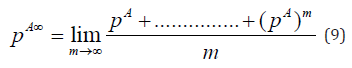
From [4], A always exists.
From [5], its fundamental matrix QA always exists.
The fundamental matrix QA is written as the fundamental matrix QA is written as

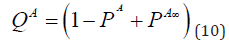
Under the hypothesis that A contains only one irreducible set of states (i.e. one subchain), the following Theorem holds:

• Theorem 1

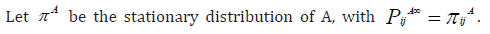
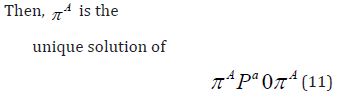
Let B be an N -state stationary Markov chain. Let PB be its transition matrix. Let PB be ’close’ to PA (in the meaning which will be specified in the following). π^B is expected to be close to π^A .

The sub chains of the chains are now hypothsised not to overlap. Let U^AB be the differential matrix such that

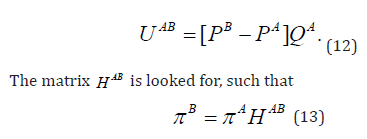
with π^B normalised as a probability distribution.
The aim of the following theorem is to obtain πB and the fundamental matrix
Q^B from π^A, Q^A, U^AB.
It is necessary to remark that there exists the matrix HAB such that

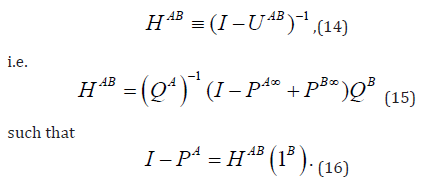
If A contains only one subchain, and if B contains only one subchain, the following theorem holds: Theorem 2

The statements are given: after

The following statement is taken from the proof of Theorem 2: Statement:
Let β be defined as

then

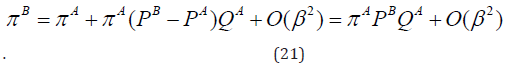
The Expression of the Perturbation Series: From [3], under the hypothesis that PB be sufficiently close to PA, the ’close- ness’ is here expressed as

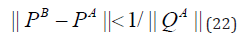
for the opportune measure (to be defined [6]); the expansion of the matrix (1-U)-1 in series of U holds.
Eq. (17), Eq. (18) and Eq. (19) become

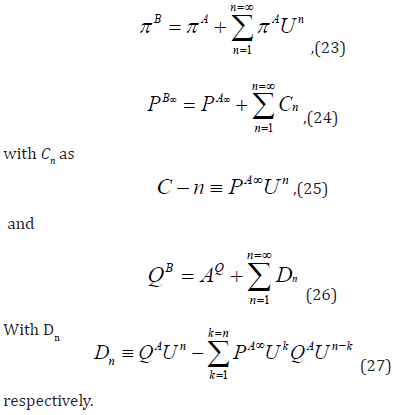
Some Qualities of Markov Chains with Generic Phase Space: Further investigations about perturbations of Markov chains are from [7], where the linear mappings of the Kernels are made use of: within the context of a generic phase space, the criteria for the strong stability and the fundamental operator are introduced. The existence and the bounded-ness of a ’fundamental operator’ T allows one to recover items of information in the cases of comparison of different objects. Given a strong stable Markov chain, every stochastic kernel Z on the neigh- bourhood of the transition kernel P obeys the relation

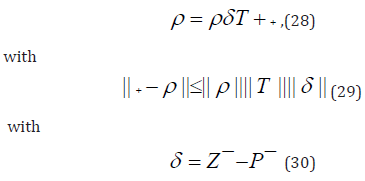
where ρ is defined in the following theorem.

• Theorem 3

Given X a Markov chain strongly stable with respect to the norm || · ||, for Y¯ a stochastic kernel in the neighbourhood of P¯, such that

Perturbations of Ergodic Markov Chains

From [8], the following definition of a ’generalised potential operator’ is reviewed. For a Markov chain X, the Korolyuk-Turbin partitions are assumed (which admit the ’zero’ state), and the Korolyuk-Turbin stationary projector Π¯ is taken. Let P¯ denote the transition kernel (and its corresponding linear operator). Let B be the Banach space.

• Theorem 4

A ’generalised potential operator’ R is well-defined on the subspace B0 = B (I − P¯+Π¯). A potential operator is a linear isomorphism between the space B0(I −Π¯) and the space B (I − Π¯) such that

Definition d

A Markov chain is strongly stable in the norm || · || if, to small perturbations (with respect to the induced operator norm) of the kernel P¯ there correspond small || · || perturbations of the invariant measure of the originating chain. Given two Markov chains with common phase space, it is possible to establish the criteria for comparisons: these procedures are useful in the comparisons of a Markov chain and its perturbed version; more in detail, in the case the perturbation of the Markov chain produces an object which is still Markovian. The following useful theorems are issued from [10]. Let B be a Banach space with norm || · ||. Let X(t) be with values in a measurable Markov chain. Let P¯ (x, A) be the transition kernel with x ∈ E, and A ∈ G; mG is the space of infinite measures in G. There exists and is unique the invariant probability matrix π¯.

• Theorem 5

X is ’uniformly ergodic’ with respect to the norm || · || if the operator Oˆ as

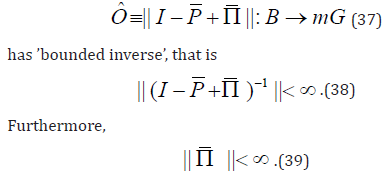
• Theorem 6

X is uniformly ergodic if is it ’strongly stable’ in this norm.

Perturbation of Geometrically-Ergodic Markov Chains

In [11], the computer-based numerical simulations of the Markov chains are critically analysed; in particular, perturbations are studied to be ascribed to finite precision and finite range, ’pseudo-random- ness’ instead of random-ness, and algorithms that involve (numerical) approximations: the present scrutiny is based on the latter instance. Be R a measurable separable space endowed with metric, and be P (x, ·) a family of transition probabilities of a Markov chain. Let the function h be denominated a ’round-off function’; the function h(x) is hypothesised to be ’close’ to x ∀x ∈ R.

The operator P (x, ·) the transition operator of the ’rounded-off’ chain.

The operator P (x, A) is defined as

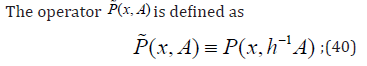
this way, the first iteration corresponds to the original chain: nevertheless, the successive iterations do not. Actually, P˜ cannot be considered a perturbation of P, as there does not exist any natural operator norm apt for this definition. The analysis of the perturbation is therefore developed after different tools. More in detail, the Markov Kernel K is defined as

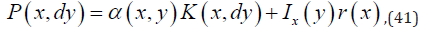
where α is the ’acceptance probability’ (i.e. for the system to move from x to y), and r is such that P must be stochastic. The ’total variation perturbations’ affect the numerical simulations. Given P a geometrically ergodic, let π¯ be the stationary distribution. There exists a finite function V, and there exist the finite positive numbers γ and b such that the ’geometrical drift condition’ is implemented after ΔV (x) defined as

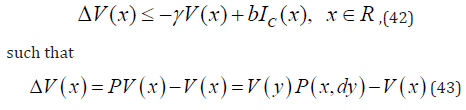
A particular Hidden Markov Model

From [12], discrete first-order HidMM can be considered. The probabilistic model describes a stochastic sequence O as

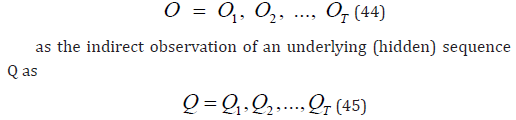
i.e. where the hidden process is Markovian. It is possible that the process is observed as not being Markovian. From [13], the qualities of the Hidden Markov Model (HidMM) can be quantified. Let M be the number of distinct observations symbols per state; the observation symbols correspond to the physical output of the modelled system: individual symbols are denoted as Vi as

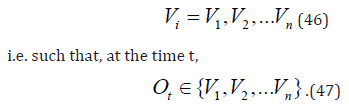
The collapse of the wavefunction has to be taken as a measurement postulate.

Proper Stochastic Markov Models

From [14], the stochastic Markov model is made use of two to achieve both statistical reconstructions and predictions with respect to the unknowns of the equations. The hypothesis is taken, that only one measurable state is available for the time series: therefore, an algorithm is proposed in order to both tailor any orders and write the transition matrix of the chain. The time series enables the probability density function and the conditional- probability density function to be constructed. The required estimators are the maximum likelihood function and the conditional expectation value. This way, it is possible to reconstruct from chaotic data.

Perturbative Theory of Ergodic Markov Chains: Numerical Approximations

From [15], it is learnt that perturbation to Markov chains implies perturbations to Markov processes. When the unperturbed chain is geometrically ergodic, the perturbations studied are uniform in the weak sense on bounded time intervals. The long-time behaviour of the perturbation chain must be investigated. Geometric ergodicity implies the exponential convergence of expectations of functions ’from a certain class’ (which will be clarified in the below). The perturbations of the chains which are due to the numerical approximations are studied.

Nearly-Gaussian Markovian-Noise Bath

From [16], to study the role of a nearly-Gaussian Markovian noise bath it is necessary to investigate on how a test system interacts with a heat bath, where the latter has a proper frequency spectrum which produces a Gaussian Markovian random perturbation. The elimination of the bath is this way performed. The relationship with the stochastic approach and the mechanical one has to be further explored. For this purpose, it is possible to envisage a partial destruction of quantum coherence of a system interacting with its environment. Quantum processes in dissipative systems can therefore be studied. The stochastic approach is here summarized. Let A be a test system; and let B be a bath, denoted as Ω = (Ω1, Ω2, ...): B is taken to have a stochastic evolution described after a Markovian equation. Be P (t, Ω) the probability to find B in the state Ωat the time t; the transition rate between Ω and Ω′ is denoted as (Ω | Γ | Ω′): the equilibrium state of Γ is | 0), i.e. such that

The decay of correlation functions in Markov processes was investigated in [17]; after this control, the Sinai Markov partitions [18] can be applied as far as the formulation of the analysis of the properties of soft matter is concerned.

Markov Approximation of Quantum Theory of Dissipative Processes

In [19], the Markov approximation is investigated to be improved after the ex- act time evolution of the density operator, the obeyance to the von Neumann conditions, and the request that the solutions should coincide with the exact density operator in the limit to a Markov process. The notion of ’open quantum system’ can be compared with that of a heat bath: the density operator is obtained in a manner such that it obeys a time-evolution equation under the hypothesis that the generator be independent of time and that the von Neumann conditions be fulfilled. The hypothesis of the exponential decay of the correlation function is taken. The Bloch equations and the density matrix can then be written in a way such that the von Neumann conditions be respected.

The Nakajima-Zwanzig Equation: The von Neumann conditions are respected at both shot time scales and longtime scale sin the Nakajima- Zwanzig equation when the first-Born approximations are made. The wished weak-coupling limit is obtained for the time evolution. After the decay of the correlation functions, the density operator becomes Markovian.

From the Von Neumann Equation to the Bloch Equation

The space-independent von Neumann equation can be derived from the Bloch equation, as in [20]. As an example, the analytical expression of the density matrix in the quantum- mechanical formalism can be recovered from a pure state of electron spin. When the Bloch equation is extended, the collapse of the wave-function is taken after the induction factor in the Landau–Lifshitz–Gilbert equation, where the latter can be reverted to a ’nonlinear variant of the von Neumann equation’.

Comparison of Computational Methods of Coarse- Graining

For generalised Langevin equations [21], the dissipative forces can be schematised as the presence of a ’memory term’. The definition of a ’memory kernel’ allows one to apply the analysis also to samples of data with large statistical noise. From model-reduction theory, form a data-driven model for the motion of particles, it is possible to extract the relevant items of information for a Markov model. The developped algorithm is one based on the ’exponential-interpolation’ method, which makes use of the Positive Real Lemma (for optimisation) for the ’model- reduction’ theory for the recovery of the associated Markov model. As an important advantage, large stochastical noise is acceptable for the implementation of the algorithm. Applications are found to ’soft-matter’ systems, also as far as ’dynamic coarse graining’ is concerned. Following the guidelines, it is necessary [22] to build Markov-State-Models (MSM’s) along pathways to determine the free-energies and the rates of the transitions. For these purposes, it is useful to study the MSM with slow re- laxation time. For the trajectories which take a shorter time than the ’slowest relaxation time’, some non-Markovian features could be expected.

These trajectories are used to reconstruct the transition probability matrix (i.e. that of the associate Markov chain studied [23]). The method is to be applied to multiple pathways, ’possibly-relaxed’ paths.

Outlook and Perspectives

The present paper is aimed at providing one with analytical expressions of finite Markov chains apt for the analytical description of biochemical materials of macromolecules, whose qualities are exptrapolated after the experimental verification of their conformational dynamics. The implementation of the Markov models which fit the experiments are formulated after the originating finite Markov chains form which the opportune Markov Models are selected. The originating finite Markov chains are to be verified to be apt for software implementation, which is achieved after ’pseudo-rando-ness’ rather than after ’random-ness’, mostly due to numerical approximations. The two causes might produce two effects on the originating Markov chain. As a first instance, perturbed Markovian objects are produced; as a second instance, non-Markovian objects are produced: the two possibilities are affected of huge theoretical differences. The tools for controlling the two different effects are explained. In the case new Markovian objects are produced, the Markovian object can be reconducted to the originating (perturbed) Markov chain, which share with the non-perturbed Markov chain a common phase space: for this reason, the notions of ergodicity and that of strong stability are introduced. In the case the new object produced is non-Markovian, the techniques of geometrically- ergodic Markov chains allow one to retrieve the wanted items of information about the non-perturbed chain.

The perturbation approaches allow one to recast the decays of the correlation functions, after which the Sinai Markov partitions can be applied. While from the perturbative approach of the originating Markov chain the collapse of the wavefunction is taken as an experimental postulate, the implementation of the decays of the correlations allows one to recover the Lan- Dau–Lifshitz–Gilbert equation, where the latter contain the ’induction factor’ which is taken as responsible for the collapse of the wavefunction. The Markovian-methods approaches to the generalised Langevin equations allow one to infer application to the description of soft matter. The Langevin equations are indeed based on irreversible dynamics of (coarse-grained) observables: no complete separation of the time scales is considered. A set of coarsegrained variables is chosen, whose time evolution contains a memory kernel. whose decay is ensured. The further degrees of freedom are treated as stochastic processes. Further studies complement the present analysis. Further characterisation of the Markov heat bath is provided with in [24]. Instead of considering the correlation decays, the ’convergence times’ of Markov chains are considered in [25]; more in details, ergodic Markov chains are analysed within this viewpoint in [26]. In [27] and [28], further techniques of comparison of Markov chains are presented.

Not applicable.

1. LT Da, FK Sheong, DA Silva, X Huang (2014) Application of Markov State Models to simulate long-time-scale dynamics of biological macor- molecules. Adv Exp Med Biol 805: 29-66.
2. P Ghosh, S Ghosh, K Basu, SK Das (2007) A Markov-model-based analysis of stochastic biochemical systems. Comput Syst Bioinformatics Conf 6:121-132.
3. PJ Schweitzer (1968) Perturbation Theory and Finite Markov Chains. Journal of Applied Probability 5(2): 401-413.
4. AT Bharucha Reid (1960) Elements of the Theory of Markov Processes and their Applications. McGraw-Hill, New York 132(3435): 1224.
5. JG Kemeny, JL Snell (1960) Finite Markov Chains. Van Nostrand, New York.
6. OM Lecian, in preparation.
7. B Rabta, D Aissani (2018) Perturbation bounds for Markov chains with general state space. Journal of Mathematical Sciences 228(5): 510.
8. NV Karthashov (1996) Strong stable Markov chains. De Gruyter.
9. NV Kartashov (1986) Inequalities in theorems of ergodocity and stability for Markov chains with common phase space. I Theory of Probability & Its Applications 30(2): 247.
10. NV Kartashov (1984) Criteria of uniform ergodicity and uniform stability for Markov chains with common phase space, Teoriya Veroyatnostey Matem- aticheskaya Statistika 30: 65-81.
11. GO Roberts, JS Rosenthal, PO Schwartz (1998) Convergence properties of perturbed Markov chains, Journal of Applied Probability 35(1): 1-11.
12. LL Wei, JQ Jiang (2010) A Hidden Markov Model based K-means time series clustering algorithm. IEEE International Conference on Intelligent Computing and Intelligent Systems, Xiamen, China, pp. 135-138.
13. Z Jiangping, D Jiangjiao, W Chengrong (2010) A new distance measure for hidden Markov models, Expert systems with applications 37(2): 1550-1555.
14. M Jokar, H Salarieh, A Alasty (2019) On the existence of proper stochastic Markov model for statistical reconstruction and prediction of chaotic series, Chaos, Solitons & Fractals 123: 373-382.
15. T Shardlow, AM Stuart (2000) A perturbation theory for ergodic Markov chains and applications to numerical approximations. SIAM Journal on Numerical Analysis 37(4): 1120-1137.
16. Y Tanimura, R Kubo (1989) Time evolution of a quantum system in contact with a nearly-Gaussian Markovian noise bath. J Phys Soc Jpn 58: 101-114.
17. NI Chernov (1998) Markov Approximations and Decay of Correlations for Anosov Flows. Annals of Mathematics Second Series 147(2): 269- 324.
18. YaG Sinai (1968) Markov partitions and C-diffeomorphisms. Funct Anal Its Appl 2: 61-82.
19. AJ van Wonderen, K Lendi (1995) Quantum theory of dissipative processes: The Markov approximation revisited. J Stat Phys 80: 273–305.
20. LV Wang (2022) Derivation from Bloch equation to von Neumann equations to Schroedinger-Pauli Equation. Foundations of Physics 52: 61.
21. N Bockius, J Shea, G Jung, F Schmid, M Hanke, et al. (2021) Model reduction techniques for the computation of extended Markov parameterizations for generalized Langevin equations. J Phys Condens Matter 33(21).
22. AC Pan, B Roux (2008) Building Markov state models along pathways to determine free energies and rates of transitions. J Chem Phys 129(6): 064107.
23. OM Lecian, in preparation.
24. M Dyer, C Greenhill, M Ullrich (2014) Structure and eigenvalues of heat-bath Markov chains, Linear Algebra and its Applications 454: 57-71.
25. I Brosh, Y Gerchak (1978) Markov chains with finite convergence time. Stochas- tic Process. Appl 7(3): 247-253.
26. B Lindqvist (1981) Ergodic Markov chains with finite convergence time. Stochas- tic Process. Appl 11: 91-99.
27. M Dyer, LA Goldberg, M Jerrum, R Martin (2006) Markov chain comparison. Probab Surv 3: 89-111.
28. P Diaconis, L Saloff Coste (1993) Comparison theorems for reversible Markov chains. Ann Appl Probab 3(3): 696-730.