Machine Learning for Enhanced Heat Transfer: LMT-ABPNN Modeling of Hybrid Nanofluid Flow on a Vertical Plate Volume 57- Issue 1

Imran Abbas*

• Department of Mathematics, Air University, Islamabad, Pakistan

Received: June 15, 2024; Published: June 21, 2024

*Corresponding author: Imran Abbas, Department of Mathematics, Air University, Islamabad, Pakistan

DOI: 10.26717/BJSTR.2024.57.008954

Abstract PDF

In recent times, there has been a notable surge in the interest of researchers in soft computing and machine learning methods. The primary reason for their value in many artificial intelligence applications is attributed to their resilient nature, exact modeling capabilities, simulation capability, and efficient assessment functionalities. This study uses Levenberg Marquardt Technique and Artificial Back Propagated Neural Networks (LMT- ABPNN) to analyze the continuous free convection flow of a hybrid nanofluid across a vertical plate. The governing partial differential equations that describe the flow are converted into a system of ordinary differential equations through the use of a similarity transformation. Subsequently, numerical methods are employed to solve this transformed system. The analysis and discussion focus on the impact of copper nanoparticle volume fractions ϕ2 on the velocity f′(η) and temperature θ(η). The findings indicate a negative correlation between velocity and temperature, as the value of ϕ2 grows. It has been found that the rate of heat transfer at the surface becomes more pronounced as the value of ϕ2 increases. In addition, it has been observed that the rate of heat transfer for the hybrid nano uid is higher compared to that of the conventional nanofluid.

Keywords: Hybrid Nanofluid; Boundary Layer Flow; Heat Transfer; Free Convection; Vertical Plate; Leven berg Marquardt Technique with Artificial Back Propagated Neural Networks

In recent years, there has been a growing interest among researchers, notably those in the eld of nanofluids, regarding the importance of fluid flow over boundary walls. This interest stems from the wide range of applications that such flow has in various engineering and industrial sectors. There is an increasing focus on the study of the medicinal and cooling qualities of mechanical instruments, such as those used in nuclear reactors, biological processes, electronics, and other related fields. [1-3]. The day when Khan and Pop made a nanofluid analysis along a sheet [4], interest increased rapidly due to combining the application of nanofluid and sheet. Different scholars extended the classical work of Khan and Pop [4] by observing the impact of pertinent parameters [5-10]. Similarly, Mohammadein and Jamshaid et al. examine the convective heat transfer using the base model of Tewari and Das [10,11]. Research on nanofluid flow problems, along vertical plate are extended by Kuznetfov and Nield [12,13]. Recently, Mahabaleshwar et al. studied the Newtonian fluid ow passed a porous stretching sheet with CNTS effects [14]. MHD Impact with slip and mass transportation examined by Vishalakshi, et al. [15]. In recent years, there has been a notable increase in the interest surrounding the investigation of heat transfer characteristics within engineering and industrial contexts. Choi and Eastman [16] were the pioneers in introducing a heat transfer fluid with enhanced performance, known as “nano fluid.”

The term “nano fluid” denotes a fluidic medium that consists of a primary fluid with nano-scale particles dispersed throughout it. Research findings have demonstrated that the rate of heat transmission in nanofluids is arugmented in comparison to conventional fluids. In contrast to conventional nanofluids that comprise a singular type of nanoparticles, hybrid nanofluids are composed of two separate types of nanoparticles. This composition has the potential to enhance heat transfer performance, since it is influenced by the presence of the second type of nanoparticles. As a result, other associated applications, such as the utilisation of hybrid nanofluid as a coolant in machining processes, are being contemplated. Recently, there has been a significant amount of scholarly discourse surrounding the numerical calculations pertaining to the flow characteristics of hybrid nanofluids. This emerging area of research has garnered considerable attention within the academic community. An investigation conducted by Devi and Devi [17] explored the characteristics of ow and heat transmission over a stretching surface using a hybrid nanofluid including Cu-Al₂O₃ nanoparticles. It was observed that the heat transfer rate is comparatively greater in relation to the nanfluid containing a singular sort of nanoparticles. Subsequently, Devi and Devi [17] expanded upon the aforementioned problem by considering three-dimensional flows and incorporating a distinct surface heating condition known as Newtonian heating.

The stagnation-point ow along a wavy cylinder surface in a hybrid nanofluid containing titania and copper nanoparticles was investigated by Youse, et al. [18]. In their study, Waini, et al. [19] examined the characteristics of unsteady hybrid nanofluid flow on a surface that undergoes stretching or shrinking. Their investigation revealed the presence of non-unique solutions. The temporal stability of the solutions was examined, revealing that just one solution exhibited both stability and physical reliability over time. Several research examining various physical features have been documented, including the work conducted by Waini, et al. [19] as referenced in [20-27], among other researchers, have conducted studies in this eld. Furthermore, the issue of nanofluid or hybrid nanofluid has been extensively discussed in the publication authored by Das, et al. [28]. Artificial neural networks (ANNs) play a crucial role in the eld of artificial intelligence since they possess the capacity to reconstruct and generate models based on non-linear phenomena. Artificial neural networks possess a diverse array of applications spanning multiple disciplines, encompassing system identification, sequence recognition, process control, sensor data analysis, natural resource management, quantum chemistry, data mining, pattern recognition, medical diagnosis, nance, visualization, machine translation, and social network filtering.

Artificial neural networks (ANNs) are characterized by their multidimensional nature and their ability to assimilate incoming data as they undergo the learning process. Artificial neural networks (ANNs) are well recognized for their effective and practical use of stochastic numerical techniques, particularly in the eld of backpropagation. The backpropagation algorithm is a supervised learning technique that use a gradient descent algorithm to minimize the error gradient, hence reducing the likelihood of errors being seen. The backpropagation method was first presented by Paul Werbos in 1974 and subsequently found independently by Rumelhart and Parker. The use of the backpropagation algorithm is prevalent in the context of feed-forward multilayer neural networks, with the primary objective of facilitating the learning process. The Levenberg Marquardt (LM) backpropagation method is a recently developed approach within the domain of artificial neural networks (ANNs) that offers computational remedies for a range of fluid flow-related issues. The achievement of stable convergence, referred to as LBM-BN, has been accomplished by researchers via the use of a Levenberg-Marquardt back-propagating artificial neural network (ANN) in conjunction with both Newtonian and non-Newtonian fluid systems. Ly, et al. [29] conducted a metaheuristic analysis to evaluate the efficacy of LBM-BN in forecasting the shear capacity of foamed concrete.

The study focused on examining the specifications and structure of LBM-BN, with the objective of assessing its effectiveness in terms of both speed and reliability. In the research conducted by Zhao, et al. [30] the Lattice Boltzmann Method-Bayesian Network (LBM-BN) approach was used to evaluate the structural deficiencies present in reinforced concrete beams. The research conducted by Nguyen, et al. [31] investigated the utilisation of artificial neural network (ANN)- based linguistic models (LM) to improve the accuracy of robot placement. Ali, et al. [32] utilised an Artificial Neural Network (ANN) in combination with a Language Model (LM)-based training methodology to forecast the volumetric ow rate of water over a steep- crested weir. Ye and Kim [33] used the LBM-BN approach to evaluate the energy consumption of a building located in China. Bharati, et al. [34] proposed a novel systematic methodology that utilises a neuro-fuzzy system framework and self-organizing maps to analyse superconductor prediction. Artificial neural networks (ANNs) are increasingly utilised in scholarly literature to tackle practical difficulties, due to their versatile nature in the domain of fluid dynamics and their efficacy in developing deterministic computer models.

As a consequence, there has been a notable increase in the number of research publications investigating a range of subjects, including entropy-generated systems, porous ns, COVID-19, and other interconnected domains. Artificial neural network methodologies are widely employed in the domains of engineering and research due to their demonstrated efficacy in augmenting production, optimising company strategies, and fostering social progress. Artificial intelligence- based stochastic solution strategies are utilised for resolving non-linear ordinary differential equations (ODEs) that arise in fluid ow problems. This methodology successfully addresses the issues encountered in supervised learning through the utilisation of intelligent computing methodologies. [35-37] conducted a study on ohmic behaviour.

Novelty of the work

This research study presents some innovative notions related to the specified problem and soft computational model. The present study proposes the utilization of the Levenberg Marquardt Technique in conjunction with artificial back propagated neural networks (LMT-ABPNN) to investigate the effect of the evaporator outlet pressure (EOP) in a mixed hydrodynamic and solutal gravity ow model (MHDSGFM). The study focuses on the analysis of free convection how around a vertical plate in a hybrid nanofluid. The nanofluid model employed in this investigation is based on the formulation proposed by Tiwari and Das [38]. Copper (Cu) and alumina (Al₂O₃) are regarded as the nanoparticles that are dispersed in water to create a hybrid nanofluid. The datasets were generated by employing the bvp4c function provided in the Matlab software. These datasets were then utilized as targets in the training, validation, and testing processes to establish the approximate solution of the proposed LMT-ABPNN. The proposed methodology effectively analyzes the dynamics of the problem across multiple scenarios by considering the variations in relevant parameters. This analysis aims to portray the behaviors of flows, velocity, temperature pro les, Nusselt number, and skin friction coefficient. The validity and verification of the LMT-ABPNN model rely on a comprehensive evaluation of accuracy assessments, histograms, and regression analysis performed for the MHDSGFM. These evaluations are presented in both graphical and numerical formats, providing adequate detail.

This study investigates the characteristics of a constant free convection ow and heat transfer occurring in the vicinity of a vertical plate, utilizing a hybrid nanofluid. The constant temperature of the plate is denoted as Tw. The following equations govern the ow [12] which can be read as:

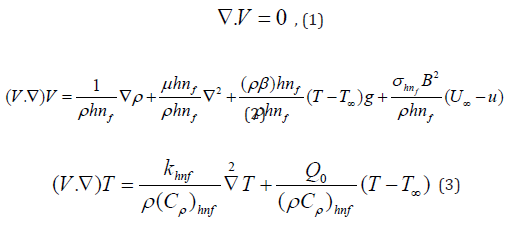
where V = (u, v), T, p, g and 2 denote the velocity, hybrid nanofluid temperature, pressure, gravitational acceleration, and Laplacian operator, respectively. Further μ_hnf, ρ_hnf, β_hnf, (ρCp) _hnf and k_hnf are the hybrid nano fluids values for its dynamic viscosity, density, coeffcient for thermal expansion, heat capacity, and the thermal conductivity respectively where the equations to evaluate their thermo-physical characteristics are provided in the following equations [26]:
Dynamic Viscosity:

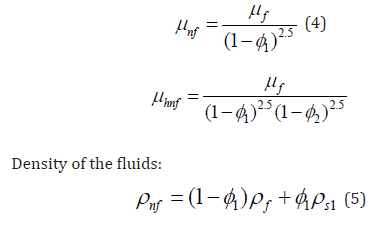
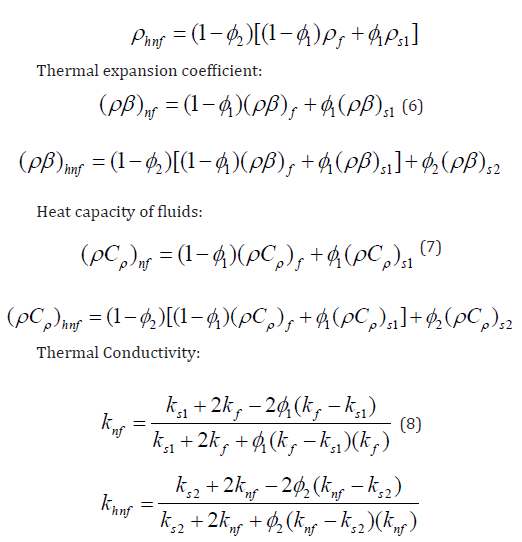
The equations (4,5,6,7 & 8) display the volume fractions of Al2O3 and Cu nanoparticles, denoted by ϕ1 and ϕ2 respectively. A value of ϕ1 = ϕ2 = 0 indicates a fluid that is not infused with nanoparticles In this study, we investigate the ow and heat transfer properties of a Casson hybrid nanofluid using a two-dimensional stable mixed convection boundary layer. The Casson parameter, denoted as C0, is employed to describe the relevant parameter in the analysis. The examination of heat transport entails the contemplation of both heat sources and heat sinks. A coordinate frame is chosen in a manner that aligns the x-axis parallel to the surface of the sheet, while the y-axis is used to measure the normal to the surface. A positive number along the y-axis is anticipated for the normal to the surface. The variable U∞(x) represents the velocity of the ow at a significant distance from the plate. Conversely, the quantity denoted as uw(x) represents the rate of change of velocity at which the sheet is undergoing either expansion or contraction. Furthermore, the symbol Tw(x) is used to represent the temperature of the surface, whereas T∞ is used to describe the unchanging ambient temperature. The manufacturing process of nanofluids commences with the initial step of systematically introducing alumina nanoparticles into the base fluid (BF). This procedure leads to the formation of a nanofluid consisting of a mixture of Al₂O₃/ water. The process of producing the hybrid nanofluid Cu−Al₂O₃/water involves treating the Al₂O₃/water nanofluid with copper nano-particles. (Table 1) presents thermophysical parameters of water, copper, and aluminum oxide. Following the theoretical model and making the assumption of the Boussinesq and BL approximation, the governing equations of the problem are as follows

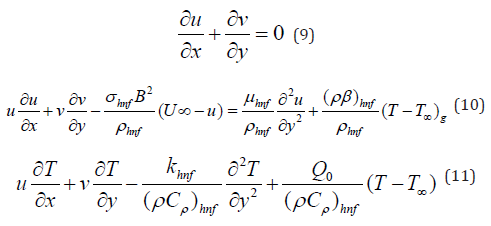
Subject to boundary conditions, which are as follows

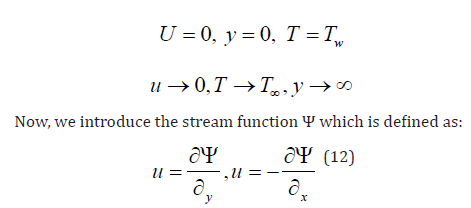
Therefore, the equation (9) is satisfied identically. According to Kuznetsov, et al. [12], we introduce the similarity variables,

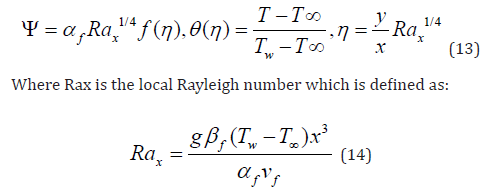
Similarity variables are then substituted into equations 10-11 to get the following ordinary (similarity) diffe erentiation equations:

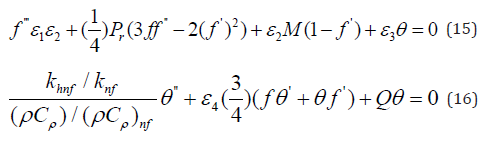
where, the formula for the terms ε₁ , ε₂ , ε₃ and ε₄ can be seen from the following (Table 2). Whereas the boundary conditions are changed to read as follows:

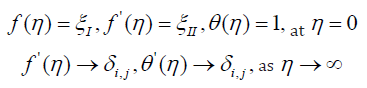
Also, αf denotes the base fluid thermal diffusivity, and primes stand for differentiation in relation to η, whereas the magnetic field parameter is denoted by M along heat source/sink by Q. On the other hand, C0 refers to the Casson parameter, the mixed convection parameter is denoted by Λ. Also, δi,j represents the constant value for different arguments. These parameters are defined as follows:

Table 1: Thermophysical characteristics of the BF and the nano- particles.

Table 2: The formula for the terms ε₁, ε₂, ε₃ & ε₄ [26].

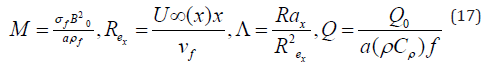
In engineering problems, two important physical quantities are the shear stress rate, which can be quantified by the skin friction coefficient, and the rate of heat transfer, which can be quantified by the Nusselt number. The formulae for N_ux & C_f, can be elaborated as:

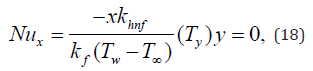
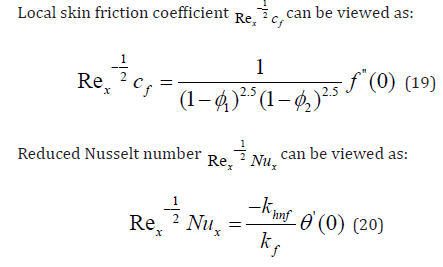
Validation

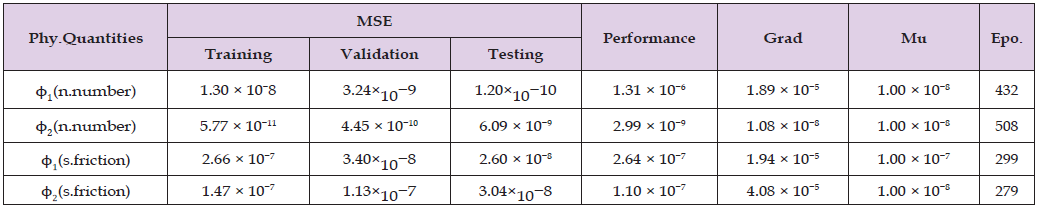
We have presented the values of −θ′ (0) for a case where (ϕ₁ = ϕ₂ = 0), shows a regular uid. These values are shown in (Table 3) for various Prandtl (Pr) numbers. Subsequently, we have compared our current findings with previous studies under extreme conditions, revealing a remarkable agreement between our results and those from prior research. (Table 4) presents the outcomes of LMT-ABPNN concerning different variations of the local Nusselt number and skin friction coefficient for the MHDSGFM. The table includes information on the use of backpropagation networks, mean squared error (MSE) values for training, validation, and testing, as well as the total number of iterations/epochs and the time required for all the MHD-SGFM scenarios.

Table 3: Value of θ′(0) for regular uid (ϕ₁ = ϕ₂ = 0) with various values of P r.

Table 4: Results of LMT-ABPNN for local nusslet number (n.number) and skin friction coefficient (s.friction) with ϕ₁(Cu/water) and ϕ₂(Cu − Al₂O₃/water).

(Figure 1a) the graph depicts the optimal validation performance of the model at each epoch, with the objective of reducing validation loss progressively. The train loss exhibits a quick decline, reaching a plateau at epoch 20, but the validation loss has a slower rate of decrease. The smallest validation loss of the model observed at epoch 83 is 8.3346e-11, suggesting that the model is effectively avoiding ovefitting to the training data. (Figure 1b) the graph illustrates the average squared error (MSE) of a deep learning model utilized for the prediction of the Nusselt number, a significant parameter in the eld of heat exchanger construction. The mean squared error (MSE) of the model exhibits a decreasing trend in the earlier stages, followed by a plateau at epoch 70, which suggests a high level of accuracy. The epoch that yields the highest validation performance is epoch 70, where the mean squared error (MSE) is recorded as 5.7722e-11. g 1(c) provided graphic exhibits the optimal validation performance of a deep learning model in the prediction of the skin friction coefficient, a critical parameter in the elds of aerodynamic and hydrodynamic design. The mean squared error (MSE) serves as a metric for evaluating the accuracy of a model, where a smaller MSE value signifies more accurate predictions. The epoch at which the highest validation performance is observed is epoch 1000, with a mean squared error (MSE) value of 1.5262e-12. This result suggests that the model has strong generalization capabilities. The proposed model offers the capability to forecast the skin friction coefficient pertaining to novel airplane and vehicle designs. This has the potential to diminish the necessity for wind tunnel experiments and facilitate the development of more streamlined and hydrodynamic items. Consequently, this advancement could result in energy conservation and a decrease in emissions. (Figure 1d) The graph illustrates a notable initial decrease in the mean squared error (MSE) of the model, followed by a stabilization phase occurring approximately around epoch 100. This implies that the model has acquired the ability to accurately forecast the skin friction coefficient. The epoch at which the highest validation performance is attained is epoch 500, exhibiting a mean squared error (MSE) of 1.5262e-12. The obtained outcome is very commendable, indicating a high likelihood of the model’s ability to effectively extrapolate to novel data. The model predicts skin friction coefficient for new aircraft and vehicle designs, reducing wind tunnel tests and promoting more aerodynamic and hydrodynamic objects, potentially leading to energy savings and reduced emissions. (Figures 2) depict the degrees of convergent efficiency, perfection, and accuracy in resolving the scenarios of Nusslet and skin friction coefficients. The time point at which the highest level of validation performance was attained was identified as the most exceptional. This observation illustrates that all lines display a consistent level of smoothness and converge towards a shared point, so concerning the concept of an ideal performance.

Figure 1

Figure 2

(Figure 3a) The error histogram shows that the model accurately predicts local Nusselt numbers, with most errors being small, with less than 5 greater than 10. However, some outliers occur due to the complexity of the problem, which can be affected by various factors. (Figure 3b) The error histogram is a useful tool for assessing uncertainty in the prediction of the local Nusselt number, indicating high uncertainty in the prediction. This information can guide experiment design or develop more conservative engineering designs. (Figures 3c & 3d) illustrates the distribution of the skin friction coefficient across 20 distinct bins. The skin friction coefficient exhibits its maximum value in the initial bin and thereafter diminishes as the bin number increases. This phenomenon can be attributed to the fact that the first bin typically encompasses the highest Reynolds values. The graph additionally illustrates a considerable degree of variability in the skin friction coefficient, even among Reynolds numbers that are similar in magnitude. The skin friction coefficient is influenced by several factors, including surface roughness and the existence of turbulence. (Figures 4a & 4b) The autocorrelation plot reveals a significant association between the error and time lag at lower values, whereas the strength of this correlation diminishes considerably as the time lag grows.

Figure 3

This implies that the discrepancy observed at a given time step is expected to exhibit similarity to the discrepancy observed at the subsequent time step, while it is improbable for the discrepancy to exhibit similarity to the discrepancy observed at a significant distant time step. This observed behavior is characteristic of convective heat transmission, wherein the punctuation of the local Nusselt number is attributed to the stochastic movement of fluid molecules. The temporal punctuations at a given point are expected to exhibit similarity with subsequent temporal punctuations, while displaying dissimilarity with temporal punctuations occurring at significantly distant points. The utilization of the autocorrelation graph is crucial in the development of control systems for convective heat transfer applications. The graph can be utilized to ascertain the requisite sampling frequency for precise measurement of the local Nusselt number. The graph can also serve as a tool for the development of controllers that possess the capability to mitigate the inherent variability of the local Nusselt number. (Figures 4c & 4d) illustrates the local skin friction coefficient, while also demonstrating the autocorrelation of error 1. Autocorrelation of error 1 refers to the correlation between the error term in a given period and the error term in the preceding period. The autocorrelation coefficient quantifies the magnitude of the correlation. The autocorrelation coefficient has a potential range of values between -1 and 1. A value of 1 signifies a complete positive correlation between the error terms, implying that the error term in one period serves as an exact predictor of the error term in the subsequent period. A value of -1 signifies a state in which the error terms exhibit complete negative correlation, implying that the error term observed in one period serves as a awless predictor of the opposite of the error term observed in the subsequent period. A value of zero signfies that the error terms exhibit no correlation, implying the absence of any association between the error term in one time period and the error term in the subsequent time period. (Figures 5a-5d)) The graph you sent displays the output of training, validation, and test models for an artificial neural network (ANN). The models have a high R-value, close to 1, indicating accurate prediction of the target output for various inputs. This ANN model has potential applications in machine or process performance prediction, fraud detection, data classification, and content generation. For instance, it can predict polyamide− 12 degradation by biocompatible fuels, a complex process di cult to model using traditional methods. It can also develop a sensitive sensor for detecting penta-chlorophenol, a toxic compound harmful to human health and the environment. Overall, the ANN model is a powerful tool for solving various problems.

Figure 4

Figure 5

Nano Particles Volume Fraction

The volume fraction of nano-particles is a crucial physical parameter for assessing the impact of nano-particles on fluid flow and heat transfer rate. (Figures 6 & 7) depict the impact of nano- particles volume fraction ϕ₁ and ϕ₂, on f′ (η) and θ(η) respectively for a Cu − Al₂O₃/ water hybrid nanofluid. Analysis shows an upward trend because of increment of volume fraction of ϕ₁ & ϕ₂, see (Figures 6 & 7) therefore momentum BL thickness decreases, the velocity of the fluid flow will be higher hence increment observed in the surface shear stress. The temperature profiles of the base fluid as shown in (Figures 8 & 9) are significantly more moderate than the temperature pro les of the hybrid nanofluid. It would appear that the temperature pro les and thickness of the thermal BL are increasing in conjunction with each subsequent increase in ϕ₁ and ϕ₂, therefore, the amount of heat how on the surface decreases. As a result, many different solid volume fractions of copper are added to the mixture in order to create a hybrid nanofluid consisting of copper, aluminum oxide, and water. The Prandtl number, represented by the numerical value 6.2, is utilized in our calculations. This value specifically pertains to water as the foundational fluid. In order to obtain accurate numerical results, it is necessary to maintain a constant value, as we have observed a high level of agreement [26]. The results show that there is an increase in both the standard nanofluid and the hybrid nanofluid when the value of ϕ₂ is raised from its initial value to a level that is considered to be satisfactory, such as 5%. Thus, the presence of hybrid nano-particles has a tendency to increase the domain of the relevant parameters for which solutions are present

Figure 6

Figure 7

Figure 8

Figure 9

This study use the Levenberg-Marquardt Technique in conjunction with Artificial Back Propagated Neural Networks (LMT-ABPNN) for the purpose of investigating. The present study investigates the phenomenon of continuous free convection ow of a hybrid nanofluid in close proximity to a vertical plate. The PDEs that govern the MHD SGFM were converted into ODEs by the application of a suitable transformation methodology. The dataset was acquired through the utilization of the Runge-Kutta-Fehlberg fourth-fifth order (RKF45) algorithm. This study investigates the spectrum of physical attributes including all conceivable scenarios of the LMT-ABPNN. The reference data samples were employed as targets throughout the training, validation, and testing phases in order to approximate the solution of the proposed LMT-ABPNN. The performance validation of LMT-ABPNN was carried out by t- ness evaluation utilizing the mean squared error (MSE), examination of the error histogram, and regression analysis. The LMT-ABPNN model’s validity and verification are determined through a thorough examination of accuracy evaluations, histograms, and regression analysis [39-41].

The convergence of the obtained outcomes for the minimum Mu and gradient values exhibits enhancement when the testing and training efficiency of the network improves. The LMT- ABPNN model’s validity and verification are demonstrated through a thorough examination of accuracy evaluations, histograms, and regression analysis. The convergence of the obtained endings for the minimum Mu and gradient values demonstrates enhancement as the testing and training efficiency of the network improves. The current findings were compared to the previously established results for extreme scenarios, and shown a high level of concurrence. The findings of the study indicated that an increase in ϕ2 resulted in a decrease in the velocity f′(η), while simultaneously causing an increase in the temperature θ(η). The incorporation of nanoparticles resulted in an increased heat transfer rate for the hybrid nanofluid compared to the conventional nanofluid.

Not applicable.

1. Paul McElfresh, David Holcomb, Daniel Ector (2012) Application of nanofluid technology to improve recovery in oil and gas wells. In SPE international oil eld nanotechnology conference and exhibition.
2. Kaufui V Wong, Omar De Leon (2010) Applications of nanofluids: current and future. Advances in mechanical engineering 2: 519659.
3. Ali Imran, Rizwan Akhtar, Zhu Zhiyu, Muhammad Shoaib, Muhammad Asif Zahoor Raja (2020) Heat transfer analysis of biological nanofluid flow through ductus efferentes. AIP Advances 10(3): 035029.
4. WA Khan, I Pop (2010) Boundary-layer ow of a nanofluid past a stretching sheet. Inter- national journal of heat and mass transfer, 53(11-12): 2477 2483.
5. Alin V Ro ca, Ioan Pop (2013) Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. International Journal of Heat and Mass Transfer 60: 355-364.
6. H Zargartalebi, M Ghalambaz, A Noghrehabadi, A Chamkha (2015) Stagnation-point heat transfer of nanofluids toward stretching sheets with variable thermo-physical properties. Advanced Powder Technology 26(3): 819-829.
7. Dhananjay Yadav, GS Agrawal, Jinho Lee (2016) Thermal instability in a rotating nanofluid layer: a revised model. Ain Shams Engineering Journal 7(1):431-440.
8. Shah Jahan, Hamzah Sakidin, Roslinda Nazar, Ioan Pop (2017) Flow and heat transfer past a permeable nonlinearly stretching/shrinking sheet in a nanofluid: A revised model with stability analysis. Journal of Molecular Liquids 233: 211-221.
9. SA Mohammadein, K Raslan, MS Abdel Wahed, Elsayed M Abedel Aal (2018) Kkl-model of mhd cuo-nanofluid flow over a stagnation point stretching sheet with nonlinear thermal radiation and suction/injection. Results in Physics 10: 194-199.
10. Mohamed Abdelghany Elkotb, Aamir Hamid, M Riaz Khan, Muhammad Naveed Khan, Ahmed M Galal (2021) Thermal radiation and chemically reactive aspects of mixed convection ow using water base nanofluids: Tiwari and das model. Waves in Random and Complex Media, p.1-31.
11. Wasim Jamshed, SR Mishra, PK Pattnaik, Kottakkaran Sooppy Nisar, S Suriya Uma Devi, et al. (2021) Features of entropy optimization on viscous second grade nanofluids streamed with thermal radiation: A tiwari and das model. Case Studies in Thermal Engineering 27: 101291.
12. AV Kuznetsov, DA Nield (2010) Natural convective boundary-layer ow of a nanofluid past a vertical plate. International Journal of Thermal Sciences 49(2): 243-247.
13. AV Kuznetsov, DA Nield (2014) Natural convective boundary-layer flow of a nanofluid past a vertical plate: A revised model. International journal of thermal sciences 77: 126-129.
14. US Mahabaleshwar, KN Sneha, Huang Nan Huang (2021) An effect of mhd and radiation on cnts-water based nanofluids due to a stretching sheet in a newtonian uid. Case Studies in Thermal Engineering 28: 101462.
15. AB Vishalakshi, US Mahabaleshwar, Ioannis E Sarris (2022) An mhd fluid flow over a porous stretching/shrinking sheet with slips and mass transpiration. Micromachines 13(1): 116.
16. S US Choi, Je reyA Eastman (1995) Enhancing thermal conductivity of fluids with nanoparticles. Technical report, Argonne National Lab. (ANL), Argonne IL (United States).
17. SP Anjali Devi, S Suriya Uma Devi (2016) Numerical investigation of hydromagnetic hybrid cu al2o3/water nanofluid flow over a permeable stretching sheet with suction. International Journal of Nonlinear Sciences and Numerical Simulation 17(5): 249-257.
18. Mohammad Youse, Saeed Dinarvand, Mohammad Eftekhari Yazdi, Ioan Pop (2018) Stagnation-point flow of an aqueous titania-copper hybrid nanofluid toward a wavy cylin- der. International Journal of Numerical Methods for Heat & Fluid Flow 28(7): 1716-1735.
19. Iskandar Waini, Anuar Ishak, Ioan Pop (2019) Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. International Journal of Heat and Mass Transfer 136: 288-297.
20. Iskandar Waini, Anuar Ishak, Ioan Pop (2019) Hybrid nanofluid flow and heat transfer over a nonlinear permeable stretching/shrinking surface. International Journal of Numerical Methods for Heat & Fluid Flow 29(9): 3110-3127.
21. Tanzila Hayat, S Nadeem (2017) Heat transfer enhancement with ag cuo/water hybrid nanofluid. Results in physics, 7: 2317 -2324.
22. Tanzila Hayat, S Nadeem, AU Khan (2018) Rotating flow of ag-cuo/h 2 o hybrid nanofluid with radiation and partial slip boundary effects. The European Physical Journal E 41: 1-9.
23. Maryam Subhani, Sohail Nadeem (2019) Numerical analysis of micropolar hybrid nanofluid. Applied Nanoscience 9(4): 447-459.
24. Wasim Jamshed, Asim Aziz (2018) Cattaneo christov based study of tio 2 cuo/eg cas- son hybrid nanofluid ow over a stretching surface with entropy generation. Applied Nanoscience 8(4): 685-698.
25. M Usman, M Hamid, T Zubair, Rizwan Ul Haq, Wei Wang (2018) Cu-al2o3/water hybrid nanofluid through a permeable surface in the presence of nonlinear radiation and variable thermal conductivity via lsm. International Journal of Heat and Mass Transfer 126: 1347 1356.
26. Mohammadreza Nademi Rostami, Saeed Dinarvand, Ioan Pop (2018) Dual solutions for mixed convective stagnation-point flow of an aqueous silica alumina hybrid nanofluid. Chinese journal of physics 56(5): 2465-2478.
27. Saeed Dinarvand (2019) Nodal/saddle stagnation-point boundary layer ow of cuo ag/water hybrid nanofluid: a novel hybridity model. Microsystem Technologies 25(7): 2609-2623.
28. Sarit K Das, Stephen U Choi, Wenhua Yu, T Pradeep (2007) Nanofluids: science and technology.
29. Hai Bang Ly, May Huu Nguyen, Binh Thai Pham (2021) Metaheuristic optimization of levenberg marquardt-based artificial neural network using particle swarm optimization for prediction of foamed concrete compressive strength. Neural Computing and Applications 33(24): 17331-17351.
30. Jue Zhao, Hoang Nguyen, Trung Nguyen Thoi, Panagiotis G Asteris, Jian Zhou (2021) Improved levenberg marquardt backpropagation neural network by particle swarm and whale optimization algorithms to predict the deffection of rc beams. Engineering with Computers, p. 1-23.
31. Ha Xuan Nguyen, Hung Quang Cao, Ty Trung Nguyen, Thuong Ngoc Cong Tran, Hoang Ngoc Tran, et al. (2021) Improving robot precision positioning using a neural network based on levenberg marquardt apso algorithm. IEEE Access 9: 75415-75425.
32. Md Shaheer Ali, Md Ayaz, Talib Mansoor (2022) Prediction of discharge through a sharp- crested triangular weir using ann model trained with levenberg marquardt algorithm. Modeling Earth Systems and Environment 8(1): 1405-1417.
33. Zhaoyang Ye, Moon Keun Kim (2018) Predicting electricity consumption in a building using an optimized back-propagation and levenberg marquardt back-propagation neural network: Case study of a shopping mall in china. Sustainable Cities and Society 42: 176-183.
34. Subrato Bharati, Mohammad Atikur Rahman, Prajoy Podder, Md Robiul Alam Robel, Niketa Gandhi (2019) Comparative performance analysis of neural network base training algorithm and neuro-fuzzy system with som for the purpose of prediction of the features of superconductors. In Intelligent Systems Design and Applications: 19^th International Conference on Intelligent Systems Design and Applications (ISDA 2019) held December 3-5, 19. Springer, 2021, p. 69-79
35. Muhammad Shoaib, Ghania Zubair, Kottakkaran Sooppy Nisar, Muhammad Asif Zahoor Raja, Muhammad Ijaz Khan, et al. (2021) Ohmic heating effects and entropy generation for nanofluidic system of ree-eyring uid: Intelligent computing paradigm. International Communications in Heat and Mass Transfer 129: 105683.
36. Iftikhar Ahmad, Hira Ilyas, Muhammad Asif Zahoor Raja, Zirwa Khan, Muhammad Shoaib (2021) Stochastic numerical computing with levenberg-marquardt backpropagation for performance analysis of heat sink of functionally graded material of the porous n. Surfaces and Interfaces 26(4): 101403.
37. Muhammad Shoaib, Muhammad Asif Zahoor Raja, Muhammad Touseef Sabir, Ayaz Hussain Bukhari, Hussam Alrabaiah, et al. (2021) A stochastic numerical analysis based on hybrid nar-rbfs networks nonlinear sitr model for novel covid-19 dynamics. Computer Methods and Programs in Biomedicine 202: 105973.
38. Raj Kamal Tiwari, Manab Kumar Das (2007) Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. International Journal of heat and Mass transfer 50(9-10): 2002-2018.
39. Adrian Bejan (2013) Convection heat transfer. John wiley & sons.
40. Ali J Chamkha, AM Aly (2010) Mhd free convection ow of a nanofluid past a vertical plate in the presence of heat generation or absorption effects. Chemical Engineering Communications 198(3): 425-441.
41. Wubshet Ibrahim, OD Makinde (2013) The effect of double strati cation on boundary-layerow and heat transfer of nanofluid over a vertical plate. Computers & Fluids 86: 433-441.