Predicting the Body Weight of Indigenous Sheep from Linear Body Measurement Traits Using Classification and Regression Tree Data Mining Algorithm Volume 56- Issue 4

Kefelegn Kebede¹*, Mesfin Asaminew² and Ashenafi Getachew Megersa¹

• ¹School of Animal and Range Sciences, Haramaya University, Ethiopia
• ²Department of Animal Science, Wolaita Soddo University, Ethiopia

Received: May 06, 2024; Published: May 15, 2024

*Corresponding author: Kefelegn Kebede, School of Animal and Range Sciences, Haramaya University, Ethiopia

DOI: 10.26717/BJSTR.2024.56.008875

Abstract PDF

Objectives: This study aimed to investigate the association between body weight (BW) and linear body measurements (LBMs) in indigenous sheep. Additionally, the study sought to establish a predictive model for BW using the Classification and regression tree (CART) data mining algorithm.
Materials and Methods: A total of 347 ewes were randomly selected for physical measurements. LBMs, i.e., height at wither (HW), body length (BL), chest depth (CD), chest girth (CG), rump length (RL), rump height (RH), pelvic width (PW), shoulder width (SW), head width (HW), head length (HL), cannon bone length (CBL), cannon bone circumference (CBC), ear length (EL), horn length (HL), tail length (TL), and tail circumference (TC), were recorded following the recommended FAO descriptors for sheep genetic resources. Statistical analyses, including descriptive statistics, correlation coefficients, and CART algorithm were employed to assess the impact of LBMs on sheep BW.
Results and Discussions: The correlation coefficients between LBMs and BW ranged from 0.11 (between RL and PW) to 0.97 (between HG and BL and between BW and HG). For the training dataset, the model explained 93% of the variance in BW acounted for by the LBMs. The root average squared error was found to be 1.27, suggesting that, on average, the model’s predictions deviated from the actual BWs by approximately 1.27 units. The CART analysis identified distinct nodes and partitions based on LBMs, specifically heart girth (HG), body length (BL), rump height (RH), and shoulder width (SW). The study reveals that BW can be effectively predicted using different combinations of LBMs.
Conclusion: The findings provide valuable insights for researchers seeking to understand the relationships between LBMs and BW in sheep. The developed predictive model can aid in estimating BW accurately, facilitating decision-making in livestock management. Further research should focus on validating these results using larger datasets and diverse sheep breeds. Additionally, future studies should consider factors such as age, sex, and breed effects to gain a comprehensive understanding of BW determinants in sheep.

Keywords: Algorithm; Body Weight; Data Mining; Sheep

Abbreviations: BW: Body Weight; LBMs: Linear Body Measurements; HW: Height At Wither; BL: Body Length; CD: Chest Depth; CG: Chest Girth; RL: Rump Length; RH: Rump Height; PW: Pelvic Width; SW: Shoulder Width; HdW: Head Width; HdL: Head Length; CbL: Cannon Bone Length; CbC: Cannon Bone Circumference; EL: Ear Length; HL: Horn Length; TL: Tail Length; TC: Tail Circumference

Ethiopia harbours a diverse population of sheep across various production systems and agro ecologies [1,2]. Small ruminants play a significant role in the livelihoods of resource-poor communities [3,4]. The small ruminant population in Ethiopia has been increasing due to factors such as population growth, urbanization, and climate change. This growth, coupled with the rising demand for meat in domestic and international markets, has elevated the importance of small ruminants in the country’s livestock sector [3,5]. According [5], Ethiopia possesses the largest populations of small ruminants (42.9 million sheep and 52.5 million goats) in the world. Almost the entire population (99.6% and 99.9%) respectively consists of native sheep and goats, with only a small number of crossbred sheep found mainly in research stations or their surrounding area. Despite the large size and wide distribution of sheep in Ethiopia, their productivity remains relatively low. This can be attributed to various factors, including inadequate nutrition, disease prevalence, insufficient breeding strategies, and a limited understanding of the production system. Body weight (BW) is an important economic trait in livestock production. Linear body measurements (LBMs) can be utilized by farmers to predict the BW of their animals. Predicting BW assists farmers in making informed decisions regarding breeding, feeding, medication, and pricing [6]. However, smallholder farmers in rural areas often face challenges in estimating the BW of their animals due to the lack of weighing scales, which are expensive to acquire.

Previous efforts to predict BW using multiple linear regression equations have been limited by poor predictions caused by multicollinearity issues [7-9]. To address this problem, some researchers have employed principal component and factor analyses in multiple linear regression analysis [9,10]. However, data mining algorithms such as classification and regression tree (CART) offer more robust and accurate alternatives to traditional methods [6-13]. These non-parametric algorithms can handle large datasets without requiring any ambiguous parametric structure [14]. They have been successfully used in predicting BW, growth responses, age, milk yield, nutritional efficiency, energy expenditure, and clinical conditions in livestock [15-19]. However, there is a lack of information on the use CART analytical technique for BW prediction in Ethiopia. The objectives of the current study were thus twofold: i. determine the association between BW and LBMs of indigenous sheep. ii. establish a model to predict BW from LBMs using the CART data mining algorithm.

Description of the Study Area

The study was conducted in three districts (Damote-Sore, Damote- Gale, and Sodo-Zuria) of the Wolaita Zone of Ethiopia. Wolaita Soddo is located 330 km away from Addis Ababa and is situated at 6.51 - 7.35 N latitude and 37.23 - 38.14 E longitudes. The three districts were purposively selected based on sheep population density (Figure 1).

Figure 1

Data Collection

A total of 347 ewes (148 from Damote-Sore, 64 from Damote-Gale and 135 from Sodo-Zuuria) were randomly selected and used for physical measurements. In livestock, such studies are mainly carried out on females due to their larger numbers as compared to males [20-22]. Body weight (BW) and linear body measurements (LBMs) namely height at whither (HW), body length (BL), chest depth (CD), chest girth (CG), rump length (RL), rump height (RH), pelvic width (PW), shoulder width (SW), head width (HW), head length (HL), cannonbonelength (CBL), cannonbone circumference (CBC), ear length (EL), horn length (HL), tail length (TL), and tail circumference (TC) were recorded following the recommended FAO descriptors for sheep genetic resources [23]. Measuring tapes and a suspended spring balance were used to measure the respective LBMs and BW of sheep.

Statistical Data Analysis

For all statistical analyses in this study, JMP 17 Pro [24] was used.

Exploratory Data Analysis

The BW and LBMs were subjected to exploratory data analysis to get results of descriptive statistics and correlation coefficients. Descriptive statistics such as average, standard deviation, standard error, and coefficient of variation were calculated. Pearson correlation coefficient was used to estimate the degree of the linear relationship between BW and LBMs.

Classification and Regression Tree (CART) Analysis

In this study, the impact of LBMs on sheep BW was assessed using a model based on the CART algorithm [25,26]. CART is a tree-based model that identifies optimal cut-off values for LBMs that significantly influence BW. By establishing prediction rules based on the values of LBMs, CART aims to create homogeneous subgroups, referred to as “terminal nodes,” by reducing variation in the BW. In CART, the initial node is known as the “root node,” and continuous LBMs are transformed into categorical variables by applying appropriate cut-off values. Initially, all observations are placed at the impure or heterogeneous root node. The objective is to devise a rule that divides these observations and generates binary nodes that are more internally homogeneous than the root node. The tree-building process continues until it becomes infeasible, with the maximum tree size reached. To determine the most effective regression tree with appropriate complexity and fit to the training data, a 10-fold cross-validation with a one-standard error rule was employed as an error estimation method, and the corrected Akaike information criterion (AICc) value was calculated [27]. The model with the lowest root average squared error, coefficient of variation, and corrected Akaike information criteria values but the highest R2 values were selected as the optimum. The Bonferroni method is used to obtain adjusted significance values for merging and splitting criteria.

Exploratory Data Analysis

Descriptive statistics results for BW and LBMs namely heightat- whither, body length, chest depth, chest girth, rump length, rump height, pelvic width, shoulder width, head width, head length, cannon bone length, cannon bone circumference, ear length, horn length, tail length, and tail circumference are expressed as mean, standard deviation, coefficient of variation, minimum, and maximum in the Table 1 below. The degree of linear association among the LBMs measured by the Pearson correlation coefficient (r) and their statistical significance are presented in Table 2. The correlation coefficients varied from 0.11 (between RL and PW) to 0.97 (between HG and BL and between BW and HG). Among 107 possible pairs of correlations, all pairs of correlations were found significant. Such positive and significant correlation coefficient values have also been reported in sheep by the studies of [28,29]. BW was positively correlated, with a statistical significance at p < 0.05, with all the LBM traits. In line with the current study, previous studies also reported a positive and statistically significant correlation between BW and body length (BL) [26]. Additionally, heart girth (HG) and BWT were observed to have a statistically significant correlation by [30]. Positive correlations suggest that selection for a trait also leads to a correlated response in the other trait, thus providing a basis for the genetic manipulation and improvement of animals.

Table 1: Descriptive statistics of BW and LBMs (n = 347).

Note: SE-standard error of mean; STD-standard deviation; CV- coefficient of variation; Min.- Minimum; Max.-Maximum. The mean body weight was 25.2 kg while for the LBM traits average values were 70.5 cm (HG), 63.3 cm (HW), 63.6 cm (BL), 17.0 cm (PW), 16.5 cm (SW), 29.7 cm (CD), 9.2 cm (HdW), 18.0 cm (HdL), 16.0 cm (CbL), 9.7 cm (CbC), 29.7 cm (TL), 17.2 cm (TC), 65.4 cm (RH), 19.7 cm (RL), and 10.5 cm (EL) respectively. Rump length varied the most (CV = 40.4 %) while height at withers (CV = 5.8 %) varied the least. The descriptive statistics results found in this study agree with earlier reports by [28] and [29].

Table 2: Correlation coefficients and their statistical significance levels among BW and LBMs (n = 347).

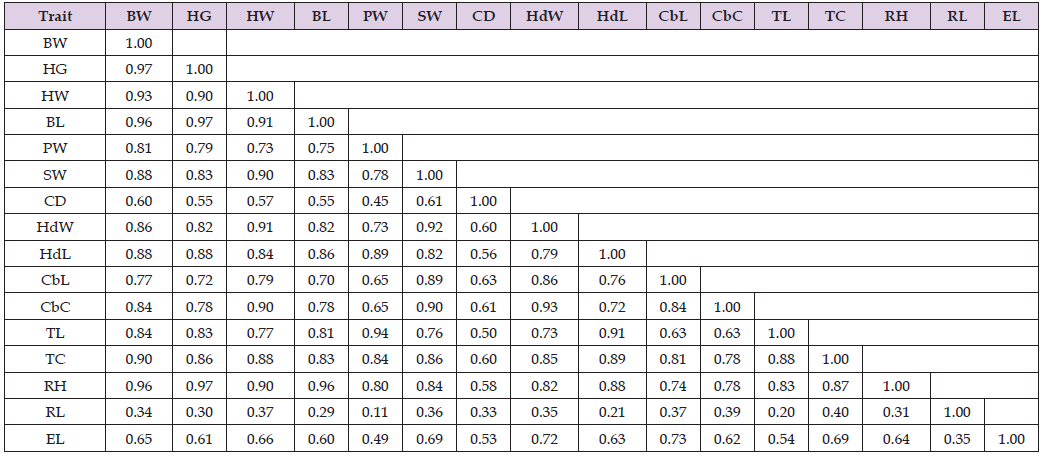
Note: significant at p<0.05 for all correlation coefficients; Bodyweight (BW); heart girth (HG); height at whither (HW); body length (BL); chest depth (CD); heart girth (HG); rump length (RL); rump height (RH); pelvic width (PW); shoulder width (SW); head width (HdW); head length (HdL); cannon bone length (CbL); cannon bone circumference (CbC); ear length (EL); horn length (HL); tail length (TL); and tail circumference (TC).

Classification and Regression Tree (CART) Analysis

LBMs are alternatives which can be used to predict BW mostly in rural areas where weighing scale is not available [6,31,32]. CART is the best decision tree technique for recognizing LBMs playing a critical role in the BW of animals [6,33]. In the current study, CART analysis was conducted to predict BW based on LBMs.The CART model’s performance was evaluated on both training and validation datasets Table 3. The training dataset consisted of 260 observations, and the regression tree had 8 splits. For the training dataset, the model explained R2 = 95% of the variance in BW, indicating that 95% of the variability in BW was accounted for by the LBMs. The logworth value for the partition was 68.73, indicating a significant relationship between the predictors and body weight. The root average squared error (RASE) was found to be 1.04, suggesting that, on average, the model’s predictions deviated from the actual BWs by approximately 1.04 units. The corrected Akaike Information Criterion (AICc) value was 780.59 for the training dataset. In a similar study conducted by [34], they compared the predictive performance of different data mining algorithms in predicting the BW of Mengali rams in Pakistan. They estimated R2 (0.90) which is comparable with the present study. However, [35] and [36] obtained a lower value of R2 (72% and 85%) respectively as compared to the current study. Such differences may be ascribed to wide variations in animal ages, type of breed, managerial conditions, and environmental factors.

Table 3: CART Model’s Performance.

The validation partition, comprising 87 observations, yielded an R2 = 94%, indicating a good fit between the LBMs and BW weight. The RASE for this partition was 1.28, suggesting a slightly higher average prediction error compared to the training partition. The CART diagram (Figure 2) constructed result has 16 Nodes and it provides a visual representation of the relationships between the LBMs and BW.The CART analysis identified distinct nodes and partitions based on different LBMs: heart girth (HG), body length (BL), rump height (RH), and shoulder width (SW). This result was in agreement with those reported by several authors [37,38]. These partitions allowed for the identification of subgroups within the population that exhibited variations in average BW. The root node (Node 0) represented the entire dataset, consisting of 260 observations. The mean BW of sheep in Node 0 was 25.35 kg, with a standard deviation (SD) of 4.80 kg. The initial partition based on HG resulted in two distinct nodes: Node 1 (HG < 72 cm) and Node 2 (HG ≥ 72 cm). Similarly, [13,39,40] reported that heart girth had the largest influence on the BW of Dorper rams. In disagreement with the current study, [33] reported that body length had the highest remarkable role in BW prediction followed by heart girth. Node 1 had a predicted average BW of 21.15 kg, which was lower than that of Node 2 (29.18 kg). Node 1, representing animals with HG < 72 cm, was further divided based on BL into Node 3 (BL < 61 cm) and Node 4 (BL ≥ 61 cm). In Node 3 (BL < 61 cm), the average BW was 18.95 kg (SD =1.70).

Figure 2

This partition comprised 62 observations. In Node 4(BL ≥ 61 cm), the average BW increased to 23.35 kg (SD = 1.33 kg). Within the BL < 61 group (Node 3), a further split was made based on RH. For RH values < 60 cm (Node 7), there were 19 observations with a mean body weight of 16.95 kg (SD = 1.03). For RH values ≥ 60 (Node 8), there were 43 observations with a mean body weight of 19.84 kg (SD = 1.07).For the BL ≥ 61 cm (Node 4) group, there were 62 observations with a mean body weight of 23.35 kg (SD = 1.33). Within the BL ≥ 61 cm (Node 4) group, a further split was made based on BL values. When BL was < 64 (Node 9), there were 37 observations with a mean body weight of 22.49 kg (SD = 0.93). For BL values ≥ 64 cm (Node 10), there were 25 observations with a mean body weight of 24.64 kg (SD = 0.57). Returning to the initial split, when HG was ≥ 72 cm (Node 2), there were 136 observations with a mean body weight of 29.18 kg (SD = 2.59). Within the HG ≥ 72 cm (Node 2) group, a further split was made based on RH. For RH values < 69 cm (Node 5), there were 81 observations with a mean body weight of 27.41 kg (SD = 1.46). For the RH ≥ 69 cm (Node 6) group, a subsequent split was made based on SW. When SW was < 19 cm (Node 11), there were 24 observations with a mean body weight of 30.54 kg (SD = 0.78). Within the SW < 19 cm (Node 11) group, a further split was made based on EL. For EL values < 12 cm (Node 13), there were 15 observations with a mean body weight of 30 kg (SD = 0). For EL values ≥ 12 cm (Node 14), there were 9 observations with a mean body weight of 31.44 kg (SD = 0.53).

For the SW ≥ 19 cm (Node 12) group, a subsequent split was made based on CD. When CD was < 36 cm (Node 15), there were 23 observations with a mean body weight of 32.35 kg (SD = 0.49). For CD values ≥ 36 cm (Node 16), there were 8 observations with a mean body weight of 34 kg (SD = 0). The CART analysis results demonstrate the hierarchical structure of the relationship between LBMs and BW in the sheep population. The identified nodes and partitions provide a clear understanding of how different LBMs contribute to variations in BW. The average BW and standard deviation values within each partition provide insights into the range and dispersion of BW within the identified subgroups. These findings have important implications for animal management and breeding programs. By considering LBMs such as HG, BL, RH, and SW, it is possible to predict the BW of animals and identify specific subgroups with different BW characteristics. This information can be utilized to optimize feeding strategies, monitor growth patterns, and identify potential outliers or sheep with exceptional BW.

Variable Importance

The importance of each EV in predicting the BW of sheep is presented in descending order in Table 4. The table shows the number of splits associated with each trait, their respective sum of squares (SS), and the contribution of contributions to the model.The results indicate that heart girth (HG) has the highest importance in predicting BW, as it accounts for approximately 75% of the overall contribution in the regression tree model. Body length (BL) is the second most important predictor, with a contribution of approximately 12% to the overall prediction of BW. Rump height (RH) follows in importance, by accounting for approximately 11% of the contribution in the regression tree model. Shoulder width (SW) demonstrates a relatively lower importance compared to the other predictors. It contributes approximately 1% to the overall prediction of body weight. The remaining predictor variables (i.e., HW, PW, CD, HdW, HdL, CL, CC, TL, TC, RL, and EL) do not contribute to the prediction of BW, as they have zero contribution values. These findings suggest that heart girth (HG), body length (BL), and rump height (RH) are the most important LBM traits for predicting BW in the studied sheep population. Researchers should focus on these traits when assessing the relationship between LBMs and BW. In agreement with the current study, [35] specified the CART algorithm to predict BW from chest girth and height at withers at yearling age in the indigenous sheep breeds of Pakistan.

Table 4: Linear body measurements important in predicting body weight.

Note: Others = HW, PW, CD, HdW, HdL, CL, CC, TL, TC, RL, and EL.

Terminal Leaf Report

Table 5 The terminal leaf report provides information about the mean body weight and the count of observations for each terminal leaf node of the regression tree. The terminal leaf labels are based on the conditions for chest girth (CG). The terminal leaf report provides information on the mean BW and the number of observations within each terminal leaf of the regression tree. The report revealed nine distinct terminal leaves in the CART (Nodes 5, 7, 8, 9, 10, 13, 14, 15, and 16), representing different combinations of LBMs. Each terminal leaf is identified by the condition that categorizes the observations falling within it. In leaf 1, individuals with HG < 72, BL < 61, and RH < 60 had an average body weight of 17 kg. While in leaf 2, individuals with HG < 72, BL < 61, and RH ≥ 60 had an average body weight of 20 kg. In leaf 3, individuals with HG < 72, BL ≥ 61, and BL < 64 had an average body weight of 22 kg. While in leaf 4, individuals with HG < 72, BL ≥ 61, and BL ≥ 64 had an average body weight of 25 kg. In leaf 5, individuals with HG ≥ 72 and RH < 69 had an average body weight of 27 kg; while in leaf 6, individuals with HG ≥ 72, RH ≥ to 69, SW < 19, and EL < than 12 had an average body weight of 30 kg. In leaf 7, individuals with HG ≥ 72, RH ≥ 69, SW < 19, and EL ≥ 12 had an average body weight of 31 kg; while in leaf 8, individuals with HG ≥ 72, RH ≥ 69, SW ≥, and CD < 36 had an average body weight of 32 kg. Finally, in leaf 9, individuals with HG ≥ 72, RH ≥ 69, SW ≥ 19, and CD ≥ 36 had the highest average body weight of 34 kg. These findings demonstrate the specific combinations of LBM traits that are associated with varying body weights. The regression tree analysis provides a comprehensive understanding of the relationships between these predictors and body weight, shedding light on the significant influence of particular LBM traits on weight variations [41-43].

Table 5: Terminal leaf report with mean body weight and count.

The current study used Pearson correlation coefficient to determine the association between body weight (BW) and LBMs of sheep with the use of CART algorithms to identify LBMs that can be used to estimate BW. Results of the correlation analysis indicated that there is a relationship between BW and LBMs in the studied sheep population. BW was significantly correlated with all LBM traits (p < 0.05). The CART analysis indicated that BW can be effectively predicted using a combination of LBMs. The predictors including heart girth (HG), body length (BL), rump height (RH), and shoulder width (SW) exhibited varying levels of contribution to the model. HG was the most important predictor, followed by BL and RH, while SW contributed relatively less to the model. The current study will help resource-limited farmers, researchers, and extension officers in determining the feed amount, drug dose, and market price of an animal and in improving the profitability of animal farms. It is recommended that the prediction of BW using LBMs, especially at rural areas might save farmers expenses for scales and help in decision-making for breeding purposes. However, further research and validation using larger datasets and diverse sheep breeds are recommended to confirm the generalizability of these findings. Additionally, other factors such as age, sex, and breed effects were not considered in this analysis, and their potential influence on BW should be explored in future.

1. Hassen H, Baum M, Rischkowsky B, Tibbo M (2012) Phenotypic characterization of Ethiopian indigenous goat populations. African Journal of Biotechnology 11(73): 13838-13846.
2. Melesse A, Yemane G, Tade B, Dea D, Kayamo K, et al. (2022) Morphological characterization of indigenous goat populations in Ethiopia using canonical discriminant analysis. Small Ruminant Research 206: 106591.
3. Haile A, Wurzinger M, Mueller J, Mirkena T, Duguma G, et al. (2018) Guidelines for Setting Up community-based small ruminants breeding programs in Ethiopia. Beirut, Lebanon: ICARDA, p. 38.
4. Tesema Z, Alemayehu K, Kebede D, Getachew T, Deribe B, et al. (2021) Evaluation of growth and efficiency-related traits of different levels of Boer x Central Highland crossbred goats. Heliyon 7(10): e08184.
5. (2020/21) CSA (Central Statistics Agency). Agricultural sample survey,; Volume II, Report on livestock and livestock characteristics (private peasant holdings). Statistical bulletin, 589. Addis Ababa, Ethiopia, pp. 199.
6. Eyduran E, Zaborski D, Waheed A, Celik S, Karadas K, et al. (2017) Comparison of the predictive capabilities of several data mining algorithms and multiple linear regression in the prediction of body weight by means of body measurements in the indigenous Beetal goat of Pakistan. Pakistan J Zool 49 (1): 257-265.
7. Yakubu A, Salako AE, Imumorin IG, Ige AO, Akinyemi MO (2009). Fixing collinearity instability in the estimation of body weight from morpho-biometrical traits of West African Dwarf goats. Trakia Journal of Sciences 7(2): 61-66.
8. Valsalan J, Sadan T, Venteketachalapathy T (2020) Multivariate principal component analysis to evaluate growth performances in Malabari goats of India. Tropical Animal Health and Production 52: 2451-2460.
9. Kefelegn K, Mesfin A (2023) Multivariate Multiple Regression Models Based on Principal Component Factor Scores to Predict Bodyweight from Morphometric Traits in a Population of Indigenous Sheep in Ethiopia. J Vet Sci Ani Husb 11(1): 104
10. Eyudran E, Waheed A, Tariq MM, Iqbal F, Ahmad S (2013) Predıctıon of lıveweıght from morphologıcal characterıstıcs of commercıal goat ın Pakıstan usıng factor and prıncıpal component scores ın multıple lınear regressıon. Journal of Animal and Plant Sciences 23: 1532-1540.
11. Akkol S (2018) The prediction of live weight of hair goats through penalized regression methods: LASSO and adaptive LASSO. Archives of Animal Breeding 61: 451-458.
12. Yakubu A, Oluremi OIA, Ibrahim ZN (2018) Modelling egg production in Sasso dual-purpose birds using linear, quadratic, artificial neural network and classification regression tree methods in the tropics. Livestock Research for Rural Development 30, Article #172.
13. Olfaz M, Tirink C, Onder H (2019) Use of CART and CHAID algorithms in Karayaka sheep breeding. J Kafkas Univ Vet Fak Derg 25(1): 105-110.
14. Song, YY, and LU Y ( 2015) Decision tree methods: applications for classification and prediction. Shanghai Archives of Psychiatry 27: 130-135.
15. Corron L, Marchal F, Condemi S, Chaumoitre K, Adalian P (2016) A new approach of juvenile age estimation using measurements of the ilium and multivariate adaptive regression splines (MARS) models for better age prediction. Journal of Forensic Science 62(1): 18-29.
16. Celik S, Eyuduran E, Karadas K, Tariq MM (2017) Comparison of predictive performance of data mining algorithms in predicting body weight in Mengali rams of Pakistan. Revista Brasileira de Zootecnia 46: 863-872.
17. Akin M, Eyduran E, Reed BM (2017) Use of RSM and CHAID data mining algorithm for predicting mineral nutrition of hazelnut. Pl. Cell Tissu. Organ Cult 128: 303-316.
18. Zakeri IF, Adolph AL, Puyau MR, Voha FA, Butte NF (2010) Multivariate adaptive regression splines models for the prediction of energy expenditure in children and adolescents. Journal of Applied Physiology 108: 128-136.
19. Rativa D, Fernandes B, Roque A (2018) Height, and weight estimation from anthropometric measurements using machine learning regressions. IEEE Journal of Translational Engineering in Health and Medicine 6: 4400209.
20. Bene S, Nagy B, Nagy I, Kiss B, Polgár JP, et al. (2007) Comparison of body measurements of beef cows of different breeds. Archives of Animal Breeding 50: 363-73.
21. Ndumu DB, Baumung R, Hanotte O, Würzinger M, Okeyo MA, et al (2008) Genetic and morphological characterization of the Ankole Longhorn cattle in the African Great Lakes region. Genetics Selection Evolution 40: 467-90.
22. Traoré A, Tamboura HH, Kabore A, Royo LJ, Fernández I, et al (2008) Multivariate analyses on morphological traits of goats in Burkina Faso. Archives Animal Breeding 51: 588-600.
23. (2012) FAO (Food and Agriculture Organization) Phenotypic Characterization of Animal Genetic Resources. FAO Animal Production and Health Guideline No.11. FAO, Rome.
24. (2023) SAS Institute Inc. JMP 17 Pro [Computer software]. Version 17.0. SAS Institute Inc.
25. Speybroeck N, Berkvens D, Mfoukou-Ntsakala A, Aerts M, Hens N, et al. (2004) Classification tree versus multinomial models in the analysis of urban farming systems in Central Africa. Agricultural Systems 80: 133-149.
26. Mathapo MC, Tyasi TL (2021) Prediction of Body Weight of Yearling Boer Goats from Morphological Traits Using Classification and Regression Tree. American Journal of Animal and Veterinary Sciences 16(2): 130-135.
27. Zhang H, Singer BH (2010) Recursive Partitioning and Applications (2^nd )., Springer, New York.
28. Bosenu B, Kefelegn K, Solomon G, Teka F (2014) On-farm Phenotypic Characterization of Indigenous Sheep Types in Selale Area, Central Ethiopia. Vet. Sci. and Technology.
29. Ahmed S, Kefelegn K, Kefena E (2015) Breeding Objective, Selection Criteria and Indigenous Goats in Western Ethiopia: Implications for Sustainable Genetic Improvement. Greener Journal of Agricultural Sciences.
30. Tekin ME, Tuglu A, Tekindal MA (2019) Determination of Relationship of Body Weight and Some Body Measurements by Non-linear Models in Hair Goats in Karaman Region. Eurasian Journal of Veterinary Sciences 35(2): 99-103.
31. Norris D, Brown D, Moela A, Selolo K, Mabelebele TC, et al. (2015) Path coefficient and path analysis of bodyweight and biometric traits in indigenous goats. Indian Journal of Animal Research 49: 573-578.
32. Tyasi TL, Mathapo MC, Mokoena K, Maluleke D, Rashijane LT, et al. (2020) Assessment of relationship between body weight and morphological traits of South African non-descript indigenous goats. Journal of Animal Health and Production 8(1): 32-39.
33. Tyasi TL, Eyuduran E, Celik S (2021) Comparison of tree-based regression tree methods for predicting live body weight from morphological traits in Hy-line silver brown commercial layer and indigenous Potchefstroom Koekoek breeds raised in South Africa. Tropical Animal Health and Production 53(1): 7.
34. Celik S (2019) Comparing Predictive Performances of Tree Based Data Mining Algorithms and MARS Algorithm in the Prediction of Live Body Weight from Body Traits in Pakistan Goats. Pakistan Journal of Zoology 51(4): 1447-1456.
35. Mohammad MT, Rafeeq M, Bajwa MA, Awan M, Abbas A, et al. (2012) Prediction of body weight from body measurements using regression tree (RT) method for indigenous sheep breeds in Balochistan, Pakistan. J Anim Pl Sci 22: 20-24.
36. Ahmed M, Serwan R, Parveen S, Rawaz K, Wael M, et al. (2020) ANN, M5P-tree and nonlinear regression approaches with statistical evaluations to predict the compressive strength of cement-based mortar modified with fly ash. Journal of Materials Research and Technology 9(6).
37. Afolayan RA, Adeyinka IA, Lakpini CAM (2006) The estimation of live weight from body measurements in Yankasa sheep. Czech Journal of Animal Science 51(8): 343-348.
38. Body Measurements. Livestock Research for Rural Development 23(9): 192.
39. Mokoena K, Molabe KM, Sekgota MC, Tyasi TL (2022) Predicting body weight of Kalahari Red goats from linear body measurements using data mining algorithms. Veterinary World 15(7): 1719-1726.
40. Marvellous OO, Oluwakayode MC, Osamede HO (2023) Predicting the body weight of indigenous goat breeds from morphological measurements using classification and regression tree (CART) data mining algorithm. Biotechnology in Animal Husbandry 39(1): 33-49.
41. Chitra R, Rajendran S, Prasanna D and Kirubakaran A (2012) Prediction of body weight using appropriate regression model in adult female Malabari goat. Vet. World 5(7): 409-411.
42. Kumar S, Dahiya SP, Malik ZS, Patil CS (2018) Prediction of body weight from linear body measurements in sheep. Indian J Anim Res 52(9): 1263-1266.
43. Olatunji-Akioye AO, Adeyemo OK (2009) Live weight and chest girth correlation in commercial sheep and goat herds in Southwestern Nigeria. Int J Morphol 27: 49-52.