Non-Equilibrium Shear Inversion of Polymer Brush Bilayer: An MD Simulation Study Volume 56- Issue 3

Mike John Edwards Majid Farzin*

• Independent research Physicist, Germany

Received: May 01, 2024; Published: May 07, 2024

*Corresponding author: Mike John Edwards Majid Farzin, Independent research Physicist, Germany

DOI: 10.26717/BJSTR.2024.56.008866

Abstract PDF

The polymer brush bilayer under non-equilibrium shear inversion is studied by means of MD simulations with Langevin and DPD thermostats. The temporal evolution of the shear stress reveals that there is an overshoot during shear inversion only with hydrodynamic interactions. Interestingly, the electrostatic interactions completely suppress this overshoot. The overshoot in the shear stress takes place moments after the chains stretch strongly in the opposite shear direction and before the new stationary shear is established. Therefore, it turns out that nature uses the electrostatic interactions between monomers i.e. Polyelectrolyte brushes to suppress mechanical in- stabilities in mammalian knee joints which is a very surprising outcome. The results of this study could shed light to our understanding from complex behavior of soft matter and biological systems.

Polymer brush bilayers form when linear polymer chains are densely grafted to two parallel surfaces and the top and bottom chains interpenetrate [1,2]. Polymer brush bilayers could be found in synovial joints of mammals as aggregan and in outer wall of cells as glycol [1]. There have been many theoretical and experimental researches about this system to identify its behavior in equilibrium, under stationary shear and under non equilibrium shear [3-4]. In some of these works, it has been mentioned that polymer brush bilayers show an shear stress overshoot under non-equilibrium shear inversion [3,5-7]. In this article, I show that this over- shoot exist only due to presence of hydrodynamic interactions between monomers. Polymer brush bilayers without hydrodynamic interactions is not a good lubricant due to its inter- penetration zone. Existence of hydrodynamic interactions make this system a good lubricant but in the expense of mechanical instabilities. Note that the lubricity of the polymer brush bilayers with hydrodynamic interactions can not be confirmed by MD simulations due to mechanical instabilities. However, this lubricity is predicted by the DFT and the scaling theory. In this article, I investigate three different systems by MD simulations. First, a neutral polymer brush bilayer without hydrodynamic interactions, second, a neutral polymer brush bilayer with hydrodynamic interactions and third, a charged polymer brush bilayer with hydrodynamic interactions.

In this article, I use molecular dynamic simulations in which the Newton’s equation of motion is solved to achieve each particle’s trajectory to study polymer brush bilayers under non- equilibrium shear inversion. I use two thermostats the Langevin and the DPD to study the system with and without hydrodynamic interactions. To discrete the equations of motion, I use the Leap-Frog scheme and we know that this scheme has an accuracy of Δt4. To build the atomic structure, I use the Lennard-Jones potential which comes from integrating over all quantum mechanical degrees of freedom, therefore, it is a semi-classical model of atoms. The repulsive hard-core part of the Lennard-Jones potential comes from the kinetic energy term of the Schrödinger equation and the attractive tail of it comes from the electrostatic interactions between electron cloud and the protons in nuclei. The Lennard-Jones potential is given as follows,

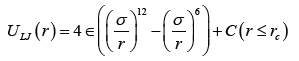
where, ϵ is the strength of the potential and σ is the diameter of the particle. Here, we cut off the potential at rc = 2^1/6σ and rise the potential with C = ϵ to produce the good solvent conditions. The walls are build by arranging the Lennard-Jones atoms in a two dimensional hexagonal close packed lattice (HCP). The finitely-extensible-nonlinear- elastic (FENE) potential is used to connect the monomers in the backbone of the chains. This potential is given as follows,

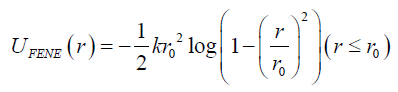
where k is the elastic constant of the FENE potential and r0 is the maximum allowed extension of the FENE potential. To mimic the presence of implicit solvent molecules as well as thermal fluctuations, I use the Langevin thermostat. The Langevin thermostat adds a fluctuating force with white noise which has the following properties,

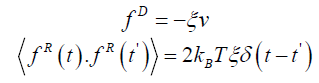
The combination of the Lennard-Jones, the FENE and the Langevin thermostat is called Kremer-Grest model [8,9] which in general is called coarse-grained model of atoms. I run the simulations for 105 time steps to achieve stationary state and I apply the step function like shear inversion protocol as follows,

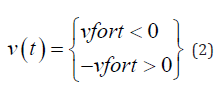
and to capture the most accurate results. Table 1 shows the numerical values of simulation parameters in my simulation [10-23]. The dissipative particle dynamic (DPD) thermostat takes the hydrodynamic interactions into account in the atomic and molecular scale. The DPD is composed of a dissipative and a random force which are given as follows,

Table 1: Numerical values of the simulation parameters.

Figure 1

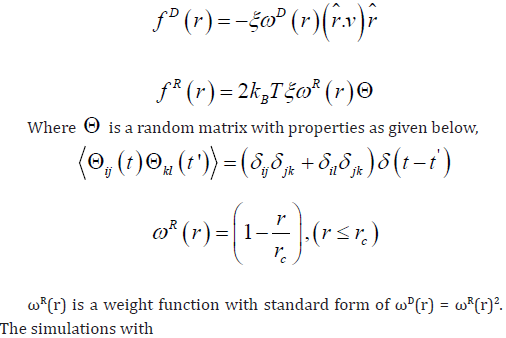
The DPD simulations run for 10 times from a same initial values and the average of the results of these 10 simulations are shown in Figure 1. The shear inversion protocol in the DPD simulations is a cosine- like protocol which is defined as follows,

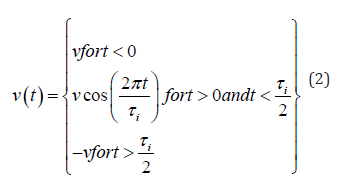
where τ_i/2 is the inversion time with the cosine protocol. The electrostatic interactions is taken into account by so called Debye-Hückel potential which is given as follows,

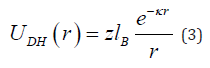
where z is valency of the monomers, l_B is the Bjerrum length and κ⁻¹ is the Debye length. The Bjerrum length is a measure of competition between the electrostatic interactions and the thermal energy and is defined as follows

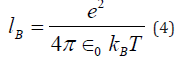
where ϵ₀ is the permittivity of the vacuum. The Debye screening length is a measure of effectiveness of the electrostatic interactions and it is given as follows,

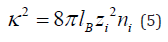
here, zi is valency of the counterions suspended in the solvent and ni is the density of counterions. The simulations for Polyelectrolyte brush bilayers run for 1.5 × 10⁵ time steps or 300 (mσ/ϵ)^1/2. The outcome of the simulations of Polyelectrolyte brush bilayers is shown in Figure 2. Note that, in these simulations I have used the cosine shear protocol shown in Eq. 2 and the results of Figure 2 are average of five different simulations with a same initial values.

Figure 2

In this article, I study polymer brush bilayers under non-equilibrium shear inversion by means of MD simulations. The simulations run for 105 time steps to achieve the stationary state and by an step function (sudden) protocol and the cosine function protocol shear inversion the direction of the shear velocity is inverted. Then I run ten simulations each for 105 time steps to achieve the stationary state in opposite direction. Note that, the simulations of Polyelectrolyte brush bilayers run for 1.5 × 10⁵ time steps to achieve the stationary state in opposite direction. It turns out that the shear stress show no overshoot during inversion without hydrodynamic interactions (see Fig. (reffig:plots)). However, simulations with the hydrodynamic interactions shows that there is an overshoot in the shear stress during the inversion (see Figure 1). Another interesting phenomenon is the behavior of chain extension in the shear direction (see Figure 3). It turns out that the shear chain extensions shrink in the first and third quarter of the inversion process time and they swell in the middle of inversion. The first minimum is related to the moment when the chains are stretched in the perpendicular direction, the maximum is related to the moment when the chains strongly stretched in the opposite direction and collide with the wall atoms and the second minimum is related to the moment when the chains after collision with wall atoms again nearly stretch in the perpendicular direction (see Figure 4).

Figure 3

Figure 4

Finally, we see that the new stationary state is established in the opposite direction Figure 4. The overshoot in the shear stress takes place in moments after the chains for the second time stretch in the opposite shear direction (figure number four in Figure 4). The overshoot in the shear stress is a cause of mammalian knee join damages and it should be suppressed. Interestingly, the simulations of Polyelectrolyte brush bilayers reveal that electrostatic interactions between monomers completely suppresses the shear stress overshoot (see Figure 2). Since, the electrostatic interactions always is present in the biological systems, it turns out that nature uses those interactions to avoid mechanical instabilities in non-equilibrium processes. This is an amazing outcome of very complex behavior of the soft matter systems with a many different types of interactions. Therefore, apparently, the synovial joint diseases which result from the lack of lubricity in the area between joint could be managed and cured by increasing charged particles. In this condition, the mechanical instabilities minimize and the motions of knee joint take place in an smooth fashion.

I am honored to acknowledge the Biomedical Journal of Scientific and Technical Research (BJSTR), the Cold Spring Harbor Laboratory (CSHL) and the Regeneron Pharmaceuticals Inc. for giving credit to my research. I also, thank Weizmann institute for the XMGrace software, the Wolfram Research for the Mathematica software and the GNU Inc. for the GFortran without which my research was not come into reality.

1. Advincula R C, Brittain W J, Caster K C, Rühe J (2004) Polymer Brushes, Wiley-VCH, Weinheim.
2. Safran S (2003) Statistical Thermodynamics of Surfaces, Interfaces, And Membranes, Boca Raton. CRC Press.
3. Kreer T (2016) Polymer-brush lubrication: a review of recent theoretical advances. Soft Matter 12: 3479.
4. Klein Jacob, Kumacheva Eugenia, Mahalu Diana, Perahia Dvora, Fetters Lewis J, et al. (1988) Reduction of frictional forces between solid surfaces bearing polymer brushes. Nature 370: 634.
5. Galuschko A, Spirin L, Kreer T, Johner A, Pastorino C, et al. (2010) Frictional Forces between Strongly Compressed, Nonentangled Polymer Brushes: Molecular Dynamics Simulations and Scaling Theory. Langmuir 26(9): 6418-6429.
6. Kreer Torsten, Binder Kurt, Müser Martin H (2003) Friction between Polymer Brushes in Good Solvent Conditions, Steady-State Sliding versus Transient Behavior. Langmuir 19(18): 7551-7559.
7. Kreer T, Müser M H, Binder K, Klein J (2001) Frictional Drag Mechanisms between Polymer-Bearing Surfaces. Langmuir 17(25): 7804-7813.
8. Smit B, Frenkel D (1996) Understanding Molecular Simulation: From Algorithms to Applications, Academic Press.
9. Kremer K, Grest G S (1990) Dynamics of entangled linear polymer melts: A molecular- dynamics simulation. The Journal of Chemical Physics 92: 5057.
10. MILNER S T (1991) Polymer Brushes. 251(4996): 905-914.
11. Halperin A, Tirrell M, Lodge T P (1992) Tethered chains in polymer microstructures. Macromolecules: Synthesis Order and Advanced Properties Springer Berlin Heidelberg Berlin Heidelberg, p. 31-71.
12. Szleifer I, Carignano M A, (2007) Wiley-Blackwell, Tethered Polymer Layers. Advances in Chemical Physics, pp. 165-260.
13. Milner S T, Witten T A, Cates M E (1988) A Parabolic Density Profile for Grafted Polymers, EPL (Europhysics Letters) 5(5): 413.
14. Zhulina E B, Borisov O V (1991) Structure and stabilizing properties of grafted polymer layers in a polymer medium. Journal of Colloid and Interface Science 144(2): 507-520.
15. Klein Jacob, Perahia Dvora, Warburg Sharon (1991) Forces between polymer- bearing surfaces undergoing shear. Nature 352: 143.
16. Taunton Hillary J, Toprakcioglu Chris, Fetters Lewis J (1988) Klein Jacob Forces between surfaces bearing terminally anchored polymer chains in good solvents. Nature 332: 712.
17. Azzaroni O, Szleifer I (2017) Polymer and Biopolymer Brushes, for Materials Science and Biotechnology.
18. Lilge I (2017) Polymer Brush Films with Varied Grafting and Cross-Linking Density via SI- ATRP. Analysis of the Mechanical Properties by AFM Springer Fachmedien Wiesbaden.
19. Mittal V (2012) Polymer Brushes, Substrates, Technologies, and Properties. CRC Press.
20. Edwards M (2018) Polymer brush bilayers at thermal equilibrium: A theoretical study.
21. Edwards M J Polymer brush bilayers under stationary shear motion at linear response regime. A theoretical approach.
22. Edwards M J Polymer brush bilayers under stationary shear motion at nonlinear response regime. A theoretical approach.
23. Edwards M J Polymer brush bilayer under stationary shear: A joint DFT. scaling theory and MD.