Generalized Doppler Effect in Wave Interaction with Uneven Moving Boundaries of Mobile Environments Volume 56- Issue 2

Glushchenko AG*, Glushchenko VA and Glushchenko AA

• Department of Physics Povolzhsky State University of Telecoimmunications and Informatics, Russia

Received: April 15, 2024; Published: April 25, 2024

*Corresponding author: Alexander Glushchenko AG, Department of Physics Povolzhsky State University of Telecommunications and Informatics, Samara, Russia

DOI: 10.26717/BJSTR.2024.56.008836

Abstract PDF

The features of reflection and transmission of waves through unevenly moving interfaces between moving media are considered. With uniform motion of the interface between the media, a stationary shift in the frequency of the reflected wave is observed for the wave reflected from the interface (Doppler Effect). It has been established that when waves are reflected from a non-uniformly moving interface between media, an additional frequency shift occurs, non-stationary in time. Analytical solutions have been obtained for calculating the change in frequency of both reflected waves and waves that have passed through the moving interface depending on the parameters of the adjacent media, including both the Doppler Effect and an additional frequency shift depending on the magnitude of the acceleration of the boundary motion. It has been shown that this effect can be observed even in the absence of the classical Doppler Effect. Analytical relations are obtained for calculating the reflection and transmission coefficients of waves interacting with a moving interface between media. The dependence of the reflection and transmission coefficients on the speed of movement of the adjacent media is shown. Generalized conditions for the absence of waves reflected from the moving interface between the media are obtained, which are realized under certain ratios of the parameters and velocities of the adjacent media.

Keywords: Generalized Doppler Effect; Boundary Motion; Separation of Media; Acceleration; Reflection Coefficient; Transmission

In medical diagnostics and measurement technology, devices are widely used that work using the Doppler Effect - changing the frequency of signals reflected from moving objects [1-3]. This effect is widely used in the technology of remote measurements of the speed of moving objects of any nature, especially in the case of unavailability of direct measurements. It is known [4-6] that the Doppler Effect underlies modern theories about the Universe [7]. Numerous varieties of the Doppler Effect are known and experimentally recorded [8-10], including: anomalous [11-13], reverse [14-16], double [17], angular [18-20], rotational [21-23] , multimode [4], in chiral [24-26], nonlinear [27], metamedia [19] media, in acousto-optics, magnetooptics, plasmonics, etc. [28]. These varieties of the Doppler Effect significantly expand the possibilities of its use in various fields of wave technology in wide frequency ranges (optical, microwave) of waves of various physical natures (elastic, electromagnetic, etc.). At the same time, it should be noted that in practice the Doppler Effect can provide relatively high accuracy only in relatively short periods of time when measuring instruments are operating, when the speed of moving and studied objects can be considered constant during the measurement period. In this case, the conditions for uniform relative movement of the radiation source and wave receiver or a wave reflected from a uniformly moving interface between the media are met. At the same time, it is known that in the general case this condition is not met and the accuracy of measurements due to the failure to meet the conditions for the Doppler Effect is low, and conclusions based on these measurements may be erroneous.

In a number of measurement technology problems, for example, in radar problems, there is always uneven displacement or movement of interacting objects, which is called the micro-Doppler effect [10]. Under these conditions, the characteristics of the effect change over time [8,29] and taking into account the unevenness of movement becomes an important task in practice. To describe and analyze the Doppler Effect, fairly clear geometric models are usually used [1,2,26], which make it possible to analyze relatively simple situations. At the same time, to solve a wider and more complex range of problems, a less developed wave theory can be used, used in particular in [4], to study the multimode Doppler Effect in a waveguide structure in [4]. The problem of wave reflection from moving interfaces between media was considered by many authors [6] without taking into account all the parameters of the adjacent media, as an analysis of the significantly influencing characteristics of the effect shows. In particular, the influence of the movement of media adjacent to the boundary was not considered. This may be due to the fact that usually the effect of the movement of the media themselves was previously considered an effect of second order of smallness due to the relatively low speed of this movement. The analysis shows that the movement of media leads to entrainment of the wave process by these media, the emergence of non-reciprocity of the parameters of wave-guiding media for forward and backward waves, to a change in the parameters of wave structures and to a qualitative change in the physical properties of these structures.

This paper examines the features of the reflection of waves from an unevenly moving interface in the general case of moving media, the influence of the uneven movement of media adjacent to the interface on the features of changes in the frequency of elastic waves reflected and passing through the interface, for which these effects are more pronounced than for electromagnetic waves due to the low speed of these waves. It has been established that, in addition to the Doppler effect, when the boundary moves unevenly, an additional time-no stationary frequency shift is observed, determined by the magnitude of its acceleration, similar to the effect previously considered by Ritz [30]. In analytical form, relations are obtained for finding the frequencies and coefficients of reflection and transmission of waves during their interaction with non-uniformly moving boundaries of media in the general case, taking into account the movement of media adjacent to the boundary. It has been established that the frequency shift of reflected waves from an accelerated moving interface can be observed in the absence of the classical Doppler Effect and, under certain conditions, exceed the frequency shift observed due to the Doppler Effect, which determines the need to revise a number of results based on the Doppler Effect.

Let us consider the reflection of waves from a non-uniformly moving interface between two media, each of which, in the general case, can also move. Let the flat interface between two media move along the 0x axis (Figure 1). At a constant speed of movement, its coordinate is described by the dependence x(t)=ut. In this case, the well-known Doppler Effect is observed [4]. With uniformly accelerated motion of the boundary in the same direction, the change in the coordinates of the interface is described by the function:

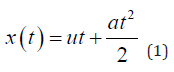
where a is acceleration. Note that the dependence of the change in the frequency of the reflected wave on the magnitude of the acceleration for the problem of accelerated approach of the source and receiver of radiation was considered by Ritz, who discovered its difference from the Doppler Effect [31-33]. In the case of accelerated motion of the boundary, the effect of changing the frequency of the wave reflected from it (and differing from the Doppler Effect) can be called the Ritz effect. The possibility of a more general case of uneven movement of the interface between media, when the coordinate of the interface between media is described by the function x (t ) = ∫u (t )dt , where u (t ) is the speed variable in time, requires a separate description. For elastic waves, physical processes are expressed more clearly due to the comparability of wave speeds and the speeds of movement of media and interfaces observed under normal conditions. For electromagnetic waves, in particular light waves, these effects, due to the high speed of light, will appear over long periods of time or when waves propagate in slow-moving media and structures. Let there be an acoustic medium to the left of the boundary (Figure 1), characterized by the density ρ₁ and speed of propagation of waves in the medium c₁ , and a medium with similar parameters, respectively ρ₂ , c₂ ,to the right. Without dwelling on the question of the practical feasibility of the model, for generality we assume that each of these media can move along the 0x axis with speeds υ₁ and υ₂. In this case, each of the media carries away the wave process with its movement. Then the speed of propagation of waves along the axis (forward waves) in the first medium is equal to c₁₀ = c₁ +υ₁ , and the speed of propagation of waves in the opposite direction (reverse waves) is equal to c_1R= c₁ −υ₁ . In the second semi-infinite medium, waves (passing through the interface between the media) propagate waves only in the direction of the 0x axis with speed c_2T = c₂ +υ₂ . There are no waves in the opposite direction.

Figure 1

The pressure functions of the incident p10, reflected p10 and transmitted p2T waves through the interface must satisfy the wave equations in the first and second media, and must also satisfy the boundary conditions on the moving interface (1), which can be represented in the form of relations [6,31]:

The choice of different frequencies for direct ω, ω₁ , ω₂ , backward and transmitted waves in (2) is determined by the Doppler effect and allows us to obtain an analytical solution for calculating the parameters of direct and reflected waves that satisfies the wave equations in both media and the boundary conditions at the moving interface between the media. Note that the change in the frequency of the transmitted wave depending on the frequency of the incident wave has not been studied previously [2,3,26], perhaps for the simple reason that this change in frequency occurs only when the parameters of the first and second media differ, that is. for a case that was not considered.

Substituting the desired solutions in the form of functions (3) into the first boundary condition (2), taking into account (1), gives the relation:

Taking into account the movement of media, relation (4) can be represented as:

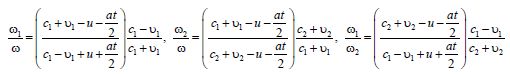
Relation (4) relates the frequencies of the reflected wave 1 ω and the wave that passed through the interface between the media 2 ω , with the frequency of the incident wave. In previous studies [1-3], they were limited to analyzing the case of a constant speed of movement of the interface between media (Doppler Effect) (u = const ) , in which the change in the frequency of reflected waves does not change with time. This approximation is mainly used in practice.

In this case, the magnitude of the acceleration is a = 0 . This approximation can also be used for uneven motion during periods of time when the condition: at <<с is satisfied, which, however, is violated over time. Over time, the speed change parameter increases and the main effect of frequency change associated with acceleration becomes. This effect also manifests itself in the general case for variable acceleration. When the relation at >c is satisfied, this effect becomes more significant than the frequency shift in accordance with the Doppler effect.

Note that the Doppler Effect is considered for the reflected wave. Therefore, it is necessary to fulfill the condition 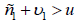when the wave catches up with the interface between the media when the first medium and the boundary are moving or, if the first medium is stationary at 1ñ > u . Generalization to the case of accelerated motion (Ritz effect) leads to the need to fulfill the relation 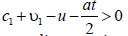(the wave catches up with the interface between the media escaping with acceleration). If the wave in the first wave moves at the speed of the interface, the effect of wave reflection is not observed. Under the condition 1 1 ñ =υ , the speed of movement of the medium reaches the speed of wave propagation. In this case, there is no reflected wave and the frequency of the reflected wave (3)1 1 ñ →υ tends to 1 ω →0 . Thus, from relation (3) it follows that the change in the frequency of reflected waves includes a time-constant component (depending on the speed of movement of the interface - this is the Doppler Effect), and a time-variable component (at constant acceleration - this is the Ritz effect). In this case, a change in the frequency of the reflected wave is observed over a limited period of time, equal to constant acceleration 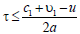, and the frequency of the reflected waves decreases 1 ω →0 over time until the moment when the speed of movement of the interface, which increases due to acceleration, reaches the speed of propagation of the incident wave.

The speed of movement of the interface between the media at this moment in time reaches the speed of the wave. During this time, the interface between the media shifts by a distance equal to

In the simplest known case of a uniformly moving interface between moving media (a=0, u≠0), from equation (4) the following relations follow:

If the media, as in commonly considered configurations, are immobile, then υ1=0, υ2=0 and general relations (3) turn into the known relations of the Doppler Effect [1,2]:

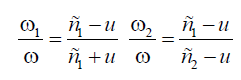
The second of these relations shows that a change in the frequency of a wave that has passed through the interface between media is observed only if these media have different wave propagation speeds c₁ (≠) c₂ . If the medium on both sides of the interface is the same, then the frequency of the transmitted wave does not change 2 ω =ω . In this case, if the interface between the media moves in the direction of propagation of the incident wave (velocities u and c1 coincide in direction, that is, the interface “runs away” from the wave), then the frequency of the reflected wave is less than the frequency of the wave. In the more general case of uneven motion of the interface between media ( a ≠ 0 ), the dependence of the relative change in the frequency of reflected and transmitted waves through an accelerated moving interface (at u/c=0.1 and u/c=0.2) on the parameter at is described by the relation (4 ) and is shown in Figure 2. The frequency shift due to the Doppler Effect depends only on speed and does not depend on time. The frequency shift occurring due to the accelerated movement of the interface becomes decisive after a time interval t~u/a even at a small acceleration a, when it reaches the value at~u. Accounting for both boundary conditions (2) gives a system of equations for determining the amplitudes of the reflected and transmitted waves, which takes the form:

Figure 2

Hence, the reflection coefficient R and the transmission coefficient T are determined by the relations:

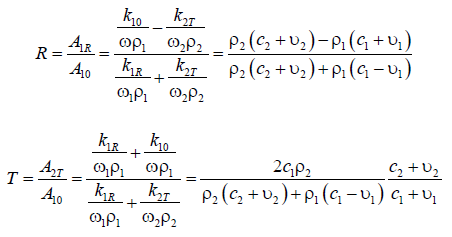
from which it follows that the coefficients R and T depend only on the parameters of the media, the velocities of the waves in these media and on the velocities of the media themselves (Figure 3). It is possible to ensure the absence of a reflected wave by fulfilling the following relation between the velocities and parameters of the media: 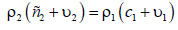. If the media are stationary, then υ₁ = υ₂ = 0 the reflection coefficient is determined by the relation:

If the second medium is stationary ( υ₂ = 0 ), then the matching condition and the absence of a reflected wave can be achieved by moving the first medium with a speed. Thus, the movement of the media can provide the condition for matching the parameters of the media, in which there is no reflection from the interface between the media.

Figure 3

The stationary change in the frequency of waves, observed when they are reflected from uniformly moving objects (Doppler effect) or interfaces between media, depends not only on the speed of movement of the interfaces, but also on the parameters of the adjacent media. The effect of changing the frequency of the reflected signal due to accelerated movement leads to a significant distortion of the results of measuring the speed of moving objects during high, even short-term accelerated movements of objects or when measuring the speed of distant objects even at low accelerations, when the parameter of the product of acceleration and time becomes comparable to the speed of the object. This shows the need to adjust the settings of multiple Doppler sensors. Coordination of the media, which makes it possible to ensure the absence of a reflected wave, can be ensured both by selecting the parameters of the adjacent media and by the movement of these media. When reflected from non-uniformly moving objects or media interfaces, an additional frequency change occurs, the magnitude of which depends on time and on the acceleration of motion. This frequency shift can also exist in those moments when the Doppler Effect is absent (the speed of the interface movement u=0).

1. Neipp C, Hernández A, Rodes Roca J, Márquez A (2003) An analysis of the classical Doppler Effect. European Journal of Physics 24(5): 497.
2. Seddon N, Bearpark T (2003) New look for the Doppler Effect. Science 302: 1537.
3. Paik A (2021) Doppler Effect and its application.
4. Glushchenko AG, Glushchenko EP, Ustinova ES (2017) Peculiarities of the Doppler Effect in a multimode waveguide. Computer Optics 41(5): 687-693.
5. Croswell K (2022) Astronomers uncover new way to measure the speed of stars, Science Writer PNAS. 119(3): e2122586119.
6. Gupta OP (1996) The Doppler Effect: A unified approach for sound and light waves. Physics Education 31(6): 31 351.
7. Daniele SD (2020) The Doppler Effect in Contemporary Physics.
8. Niu Y, Ding J, Fei D, Zhongи Z, Liu Y (2019) Doppler Effect on High-Speed Railway at 465 MHz. IEEE International Symposium on Antennas and Propagation and USNC-URSI. Radio Science Meeting, pp. 2117-2118.
9. Petrescu F (2015) Im proving Medical Imaging and Blood Flow Measurement by Using a New Doppler Effect Relationship. Am J of Eng and Appl Scien 8(4): 582-588.
10. Ying Luo, Yi-Jun Chen, Yong-Zhong Zhu, Wang-Yang Li, Qun Zhang (2020) Doppler Effect and micro-Doppler effect of vortex-electromagnetic-wave-based radar. IET Radar, Sonar and Navigation 14(1): 2-9.
11. Service B (2003) Doppler done backward. Science.
12. Kuzelev MV, Rukhadze A (2005) Anomalous Doppler Effect and stimulated Cherenkov Effect in a plasma waveguide with a thin-walled annular beam. Plasma Physics 31(8): 638-645.
13. Mazilu T, Dumitriu M (2011) On the Anomalous Doppler Effect. RJAV 8(2): 120.
14. Liu C, Long H, Zhou C, Ying Cheng, Xiaojun Liu (2020) Reversed Doppler Effect based on hybridized acoustic Mie resonances. Sci Rep 10: 1519.
15. Jiang Q, Chen J, Wang Y, Liang B, Hu J, et al. (2016) Mechanism Analysis of the Inverse Doppler Effect in Two-Dimensional Photonic Crystal based on Phase Evolution. Scient Reports 6: 24790.
16. Jiang Q, Chen J, Cao L, Zhuang S, Jin G, et al. (2018) Dual Doppler Effect in Wedge-Type Photonic Crystals. Sci Rep 8(1): 6527.
17. Garetz BA (1980) Angular Doppler Effect. J Opt Soc Am 71(5): 609-611.
18. Dholakia K (1998) An experiment to demonstrate the angular Doppler Effect on laser light. Am J Phys 66(11): 1007-1010.
19. Brasselet E (2016) Harmonic angular Doppler Effect. Nature Photonics. Nature Publishing Group 10(6): 362-364.
20. Qiu S, Jinwen W, Yang X, Cao M, Shougang Zhang, et al. (2022) Observation of the Rotational Doppler Effect with Structured Beams in Atomic Vapor. Frontiers in Physics 9: 2021.
21. Korech O, Steinitz U, Gordon RJ, Averbukh, Prior Y (2013) Observing molecular spinning via the rotational Doppler Effect. Nature Photon 7: 711-714.
22. Giuliani G (2014) On the Doppler Effect for photons in rotating systems. European Journal of Physics 35(2): 025015.
23. Zhai S, Zhao X, Liu S, Shen F, Li L (2016) Inverse Doppler Effects in Broadband Acoustic Metamaterials. Sci Rep 6: 32388.
24. Yuanfei H, Zhiwei C, Shenyan G, Yiping H (2021) Propagation dynamics of vortex electromagnetic waves in dispersive left-handed materials. Waves in Random and Complex Media 33(1): 122-135.
25. Ran J, Zhang Y, Chen X, Fang K, Zhao J, et al. (2015) Realizing Tunable Inverse and Normal Doppler Shifts in Reconfigurable RF Metamaterials. Sci Rep 5: 11659.
26. Guixin L, Zentgraf T, Zhang S (2016) Doppler Effekt in nonlinear optics. Nature Physics 12: 736-740.
27. Qimeng S, Song Q, Tong L, Weijie W, Yuan R (2021) Doppler effect of polarization grating. Applied Optics 60(10): 2788-2794.
28. Ying Luo, Yi-Jun Chen, Yong-Zhong Zhu, Wang-Yang L, Qun Z (2020) Doppler Effect and micro-Doppler effect of vortex-electromagnetic-wave-based radar. IET Radar, Sonar & Navigation 14(1): 2-9.
29. Shukri K, Berisha V (2018) The Doppler effect and similar triangles. Results in Physics 12(2019): 846-852.
30. Ritz V, Ritz W (1908) Recherches critiques surl'Électrodynamiquegéné Ann De Chim Phys 13: 145.
31. Othman M, Ali M, Farouk R (2011) Analytical Solution for Acoustic Waves Propagation in Fluids. World Journal of Mechanics 1(5): 243-246.
32. Semikov SA (2013) The Ballistic Theory of Ritz and the Pattern of the Universe. Revolution in Science and Engineering). (3^rd)., Nizhni Novgorod.
33. Seddon N, Bearpark T (2003) Observation of the inverse Doppler Effect. Science 302(5650): 1537-1540.