Mathematical Investigation for the Mechanism of the Pancreatic Juice Reflux in High Confluence of Pancreaticobiliary Ducts and Pancreaticobiliary Maljunction Volume 55- Issue 5

Tsutomu Tajikawa¹*, Keita Aoki² and Hiroaki Fukuzawa³

• ¹Department of Mechanical Engineering, Faculty of Engineering Science, Kansai University, Japan
• ²Graduate School of Science and Engineering, Kansai University, Japan
• ³Department of Pediatric Surgery, Japanese Red Cross Society, Himeji Hospital, Japan

Received: March 20, 2024; Published: April 04, 2024

*Corresponding author: Tsutomu Tajikawa, Department of Mechanical Engineering, Faculty of Engineering Science, Kansai University, Japan

DOI: 10.26717/BJSTR.2024.55.008764

Abstract PDF

ABSTRACT

Pancreatic juice reflux (PBR) to the common bile duct and gallbladder is observed in cases with pancreaticobiliary maljunction (PBM) and high confluence of pancreaticobiliary ducts (HCPBD) with various morphological characteristics of the biliary tract. However, the mechanisms underlying PBR remain unclear. The purpose of this study was to investigate the mechanisms underlying PBR from the perspective of fluid mechanics. In a previous study, we developed a mathematical model for bile and pancreatic juice flow based on the theory of fluid mechanics. A computational simulation of pancreaticobiliary flow in the morphologically normal duct without biliary dilatation and in HCPBD and PBM was performed to investigate the influence of morphological parameters of the pancreaticobiliary tract. The simulation results showed that the length of the common channel (CC) within the region of the sphincter of Oddi (RSO) and compliance of the gallbladder significantly affected the pancreaticobiliary flow regardless of whether the duct was morphologically normal or showed HCPBD or PBM. However, the CC length beyond the RSO was completely unaffected. The length of the CC within the RSO is an important factor influencing PBR without biliary dilatation. Therefore, our mathematical model is a powerful tool for understanding pancreaticobiliary flow.

Keywords: Pancreatic Juice Reflux; Pancreaticobiliary Maljunction; High Confluence of Pancreaticobiliary Ducts; Flow Simulation For Bile and Pancreatic Juice; Morphological Parameters of Pancreaticobiliary Ducts

Abbreviations: CBD: Common Bile Duct; CC: Common Channel; CD: Gallbladder/Cystic Duct; CHD: Common Hepatic Duct; Duo: Duodenum; GB: Gallbladder; HCPBD: High Confluence of Pancreaticobiliary Ducts; PBM: Pancreaticobiliary Maljunction; PBR: Pancreaticobiliary Reflux/Pancreatic Juice Reflux; PD: Pancreatic Duct; RSO: Region of the Sphincter of Oddi; SO: Sphincter of Oddi

Introduction

Pancreaticobiliary maljunction (PBM) with pancreaticobiliary reflux (PBR) into the biliary tract shows a broad spectrum of morphological characteristics, including variations in the shape and size of the pancreaticobiliary ducts. On the basis of various investigations of morphological parameters such as duct diameter and length [1-5], diagnostic criteria for PBM have been developed and updated [6-8]. In addition, some biomechanical engineers have investigated bile flow in the human biliary duct using computational flow simulation [9-15]. However, the relationship between the morphological parameters and PBR has not yet been clarified. Fukuzawa et. al. fabricated a simplified model of pancreaticobiliary ducts that modelled the structure of the human biliary tract system, including the common bile duct (CBD), gallbladder/cystic duct (CD), gallbladder (GB), common hepatic duct (CHD), and pancreatic duct (PD) in cases of PBM without biliary dilatation, and used the model to clarify the mechanism of PBR [16] and to demonstrate that PBR disappears after cholecystectomy. However, it is almost impossible to fabricate individual patient-specific models of the pancreaticobiliary duct and investigate the effects of these morphological parameters on PBR. Therefore, to generalise this problem, we developed a mathematical model for pancreaticobiliary flow in pancreaticobiliary systems based on the theory of fluid mechanics [17].

Using a mathematical model, we simulated normal pancreaticobiliary flow during the bile-refilling period, and the results showed good agreement with actual measurement data of human gallbladder volume changes [18] and the temporal variations of the intro-pressure in the contraction and relaxation of common channel (CC) by the sphincter of Oddi (SO) [19,20]. However, PBR could not be simulated in our mathematical model using statistically averaged morphological parameters of the pancreaticobiliary ducts [17]. The purpose of this study was to clarify the influence of the morphological parameters of the pancreaticobiliary ducts on PBR without biliary dilatation by using our developed mathematical model. We simulated the pancreaticobiliary flow using various morphological parameters of the pancreaticobiliary duct. This paper presents the results of a parameter study of the mathematical model of the influence of pancreaticobiliary ducts on PBR without biliary dilatation and considers the factors of pancreaticobiliary duct morphology that influence PBR.

Methods

The details of our targeted phenomena and the mathematical model are described in our previous paper [17]. We have succinctly summarised these aspects in the following sections:

Targeted Phenomena for Mathematical Modelling

This study modelled the 4–12-h period (hereafter referred to as the bile-refilling period) in which the GB volume was minimised just after a meal and bile was refilled in the GB immediately after that and by the next meal. Therefore, we assumed that the bile produced by the liver had filled all biliary tracts, and neglected changes in the density and viscosity of bile. And it was assumed that the dilatation and peristalsis of the biliary tract and the existence of accessory pancreatic ducts in the pancreaticobiliary system were negligible.

Mathematical Model and its Assumptions

From the perspective of fluid mechanics, almost all mass transport in the pancreaticobiliary duct occurs by advection rather than diffusion. Therefore, it was possible to simulate the flow phenomena in the pancreaticobiliary duct to investigate PBR. Because the bile and pancreatic juice flows during the bile-refilling period were much slower than those during blood flow, the flow could be modelled as a linear phenomenon. Thus, all pancreaticobiliary ducts in this study were modelled as mechanically equivalent straight and circular tubes with flow resistance and their combinations. In this study, pancreaticobiliary flow was modelled using an equivalent 1-dimensional hydrodynamical circuit, as shown in Figure 1 [17]. The liver and pancreas were modelled as volumetric pumps, similar to syringe pumps, with a constant flow rate. Hepatic bile and pancreatic juice flow from the GB to the duodenum (Duo) through the CD, CBD, CC, and ampulla of Vater due to the pressure difference between the GB and Duo. Apart from the CC, the PD and CBD within the region of the sphincter of Oddi (RSO) were opened and closed by SO contraction and relaxation, as shown in Figure 1a, which was a model for the morphological normality of the pancreaticobiliary duct or high confluence of pancreaticobiliary ducts (HCPBD). However, if SO contraction did not affect the CBD and CC, as shown in Figure 1b, it was a model for anomalous arrangement of the pancreaticobiliary ducts. In these models, pancreaticobiliary flow satisfied both the equations of continuity as the law of conservation of mass for flow and Bernoulli’s theory, including pressure loss as the conservation law of the energy of the flow.

The equations of continuity at bifurcations of the ducts are as follows:

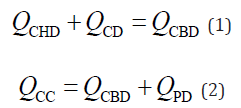
Here, the quantities of Q are the volumetric flow rates at each duct, and the subscripts indicate the location of the flow. This study defined the flow rate as positive (Q > 0) when the fluid flowed toward the Duo. When the volume of the GB was temporarily increased, the flow rate at the CD was negative (Q_CD < 0). However, the GB absorbs a portion of the water in bile juice [16]. Therefore, the GB volume change per unit time (dV_GB/dt) occurs because of the difference between the inflow rate toward the GB (–Q_CD) and the water-absorption rate (Q_D) at the GB, as follows:

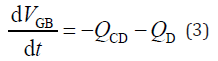
These three equations must be satisfied not only for normal pancreaticobiliary ducts, but also for HCPBD and PBM. Since the GB pressure is almost the same as the intraduodenal pressure at the start of GB refilling, hepatic bile flows from the CD to the GB. The inflow causes both the GB intra-volume and inner pressure to increase with time. The relationship between the GB intra-volume and inner pressure is modelled using compliance, known as arterial compliance, in mathematical models of the cardiovascular systems [21,22].

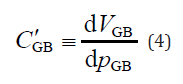
where dV_GB is the volume change in the GB cavity, dp_GB is the amount of pressure change in the GB, and C’_GB is the compliance of the GB, which is an index of its deformability.

By integrating Equation 3 and combining it with Equation 4, the following equations are obtained:

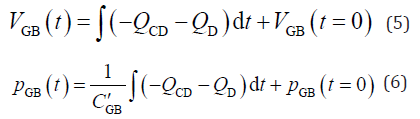
where p_GB(t = 0) is the initial intra-GB pressure at the start of bile refilling; V_GB(t = 0) is the minimum GB volume at the start of GB refilling; and t is the time elapsed from the start of GB refilling. Bernoulli’s theory, including pressure loss [23,24] without negligible terms such as the energy dissipation caused by the flow vortex, was formulated by an electronic–hydraulic analogy, as shown in Equation 7 [17].

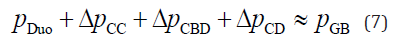
where p is the local static pressure and Δp is the pressure loss in each pancreaticobiliary duct. According to the definition of flow rate, the pressure loss is positive (Δp > 0) when the fluid flows toward the Duo. The pressure drop through a straight cylindrical tube was estimated using the Hagen–Poiseuille law [23,24], as shown in Equation 8.

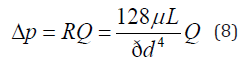
where Δp is the viscous pressure drop between the ends of the duct, R is the flow resistance of the duct, Q is the volumetric flow rate in the duct, d is the inner diameter of the duct, L is the length of the duct, and μ is the dynamic viscosity of a working fluid. The different morphologies in individual diseases, such as HCPBD and PBM, are expressed by the differences in flow resistance, as shown in Equation 8. For example, patients with normal duct morphology and HCPBD were observed to have a part of the CC, CBD, and PD within the RSO. The flow resistance of each duct has two elements that are expressed by the following equation:

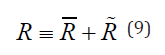
here, the quantity of R is the flow resistance of the pancreaticobiliary duct beyond the RSO, and R is the flow resistance within the RSO that is temporally varied by SO contraction and relaxation. When the CC was not observed beyond the RSO in the case of a normal pancreaticobiliary duct and HCPBD, was zero. In contrast, and were zero in the case of PBM because the CBD and PD were not observed within the RSO.

By combining and integrating Equations 1, 2, and 7–9, the flow rate at the CD was obtained as follows:

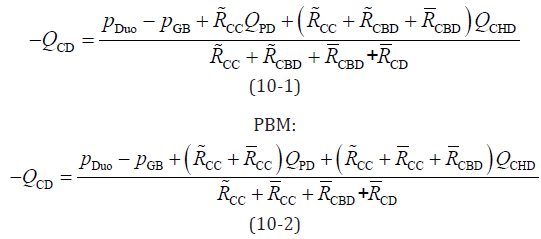
Equations 5, 6, and 10 can be solved and pancreaticobiliary flow can be simulated by applying suitable boundary conditions for the phenomena. Next, we discuss the boundary conditions and parameters used to calculate the mathematical model.

Boundary Conditions and Parameters

This study employed Fukuzawa’s baseline data setup [16] and our previous study [17] for the morphological parameters of human pancreaticobiliary ducts, as shown in Table 1. However, other physical data are required as boundary conditions to solve the mathematical model. As the intraduodenal pressure was the back pressure for the pancreaticobiliary system, this study assumed that the intraduodenal pressure was almost constant, equal to the intraperitoneal pressure and close to the atmospheric pressure.

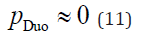
Note: Abbreviations: CD, gallbladder duct; PD, pancreatic duct; GB, gallbladder; CHD, common hepatic duct; CBD, common bile duct.

On the basis of the measurement of the relationship between healthy human GB volume and its intra-pressure change [25], we calculated the GB compliance and set it at approximately 0.35 – 12 mL/ mmHg. Therefore, in this study, changed C’GB = 1 to 15 mL/mmHg. The findings indicated that the SO was repeatedly contracted and relaxed with a 10–12 s cycle [19,20]. This study assumed that the inner diameter of the CC within the RSO was periodically changed by 0.3 mm when opened and 0.096 mm when closed repeatedly with a square waveform at 5-s intervals [17]. Furthermore, on the basis of Fukuzawa’s estimation [16], this study employed the value of the water-absorption rate QD at the GB, which was set at 23 mL/h. A summary of the common conditions for flow simulation is shown in Table 2. Further conditions for PBM and HCPBD are listed in Tables 3 & 4, respectively. This study neglected the fact that the variation in the fluid physical properties, such as viscosity and density, was due to the mixing of the bile and pancreatic juice, similar to our previous work [17]. To simplify the mathematical model, it was assumed that the viscosity and density of pancreatic juice were the same as those of hepatic bile.

Note: Abbreviations: PD, pancreatic duct; GB, gallbladder; CHD, common hepatic duct; Duo, duodenum.

Note: Abbreviations: CD, gallbladder duct; CBD, common bile duct; CC, common channel; RSO, region of the sphincter of Oddi; PBM, pancreaticobiliary maljunction.

Note: Abbreviations: CD, gallbladder duct; CBD, common bile duct; CC, common channel; RSO, region of the sphincter of Oddi; HCPBD, high confluence of pancreaticobiliary ducts.

Numerical Simulation Method

With these boundary conditions and the baseline data setup, the time variations of QCD and pGB can be calculated by combining equations 5, 6, and 10. This study revealed an estimated solution of the pancreaticobiliary flow during a bile-refilling period of 6 h by using the modified Euler numerical integration method for simultaneous equations within a 1-s interval time step with MATLAB (2020R1; MathWorks, Natick, MA, USA).

Results

Figure 2 shows an example of the simulation results for GB volume recovery and the influence of the anatomical morphological parameters on GB volume recovery. In our previous study, the simulation results obtained using our mathematical model agreed well with the GB volume recovery trend. The pressure variation and its frequency in the CC within the RSO were also accurately simulated [17]. These results indicate that the length of the CC affects the GB volume recovery rate. Therefore, to summarise the influence of the different morphological parameters of the pancreaticobiliary ducts on the PBR during the bile-refilling period, the integrated flow rate of bile at the CBD was calculated over 6 h after the start of refilling. Figures 3 & 4 summarise the simulation results. Figures 3 & 4 show the results for HCPBD and PBM, respectively. These graphs show the relationship between biliary tract size and pancreaticobiliary flow. Because the integrating flow rate is the moving volume of the working fluid, if the integrating flow rate at the CBD is less than zero (negative value), PBR occurs. The broken lines in each graph show the volumes of the CBD and CD. When the integrating flow rate at the CBD is lower than the broken line in the graph, pancreatic juice reaches to the GB within 6 h.

These results showed that the length of the CC beyond the RSO did not affect pancreaticobiliary flow in cases of PBM. In contrast, the length of the CC within the RSO and GB compliance affected reflux. When the GB compliance was approximately 5–10 mL/mmHg, which was the same as the average of the reference data [25], the pancreatic juice reflux that occurred in our simulation using the length of the CC within the RSO was over approximately 6 mm. In the case of HCPBD, the CC length was also a significant factor in pancreatic juice reflux. GB compliance affected bile and pancreatic juice flows in both cases. In the results of the simulation under average GB compliance, pancreatic juice reflux could also be observed when the length of the CC within the RSO was >6 mm. This result showed good agreement with the diagnostic criterion of the PBM as “the length of the CC is longer than 6 mm” [26]. These results indicate that the important factor in PBR might be the flow resistance of the CC, which opened and closed as a result of SO contraction and relaxation, and the compliance of the GB. Moreover, the existence of the CC beyond the RSO contributed little to reflux. However, other morphologically important factors may exist. To investigate the reason for this, we have discussed this possibility theoretically using the mathematical model.

Discussion

Consideration of a PBR-generating Mechanism Based on a Mathematical Model

According to Equation 1, if the flow rate at the CD (Q_CD) is less than zero (Q_CD < 0), the working fluid in the CD flows toward the GB. When PBR occurs, the flow rate at the CDB (Q_CDB) is negative (QCDB < 0). Therefore, PBR occurs under the following conditions:

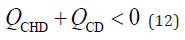
By dividing both sides of equation 12 by the flow rate at the CHD (Q_CHD) and simplifying it, the following relationship was obtained:

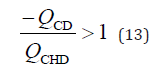
This equation indicates that PBR occurs when the CD flow rate is negative and the absolute CD flow rate is higher than the CHD flow rate. By dividing both sides of Equation 10 by the CHD flow rate and applying Equation 13, the following PBR conditions are obtained:
Normal and HCPBD:

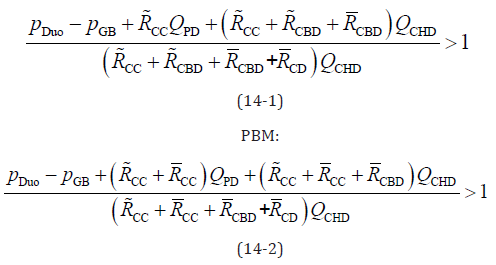
These equations indicate that the numerator of the fraction is smaller than the denominator when PBR occurs. By eliminating the same terms on the left and right sides of equation 14 and rearranging them, the simplified equation for the reflux condition is as follows:

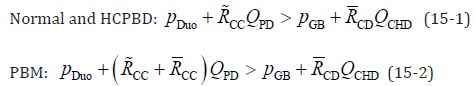
To the best of our knowledge, no reference data are available for the CC diameter when the SO contracts and relaxes. Because we could not observe the contracted CC during endoscopic retrograde cholangiopancreatography, the contracted CC may have been much narrower than the CC outside the RSO. According to the Hagen–Poiseuille law as shown in Equation 8, the flow resistance R varies in inverse proportion to the fourth power of the duct diameter. Since the flow resistance of the CC within the RSO ( ) is much higher than that of the CC beyond the RSO ( ), the resistance of the CC beyond the RSO is negligible in Equation 15-2. Therefore, the conditions for the occurrence of PBR can summarised by the following equation, regardless of whether the bile duct is morphologically normal or shows HCPBD or PBM:

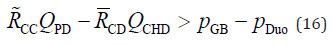
The CD diameter was much larger than that of the CC when the SO contracted. In contrast, the diameters of the CC and CD were approximately a few millimetres when the SO was relaxed. The lumen of the CD contains the spiral valves of Heister [27,28]. Because these valves are spiral-undulating folds, the working fluid in the CD has a large surface area for its volume. In other words, the flow resistance of the CD is higher than that of the CC if the SO is relaxed, and it is difficult to reflux pancreatic juice into the CBD. When the SO contracts, the flow resistance of the CC within the RSO is significantly higher than that of the CD. Thus, the conditions for reflux occurrence can be simplified as follows:

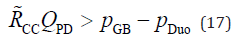
We can consider the mechanism of PBR by using this equation, as follows…First, we focus on the left-hand side of Equation 17. Because the Fukuzawa baseline setup was employed in this study, the pancreatic juice production rate was assumed to be constant. However, the rate of pancreatic juice production varies during the day depending on dietary conditions and other factors, and the rate may also show individual differences. Thus, it was assumed that the pancreatic juice production rate could change 0.5- to 2-fold rather than Fukuzawa’s baseline setup. However, as shown in Equation 8, the flow resistance of the pancreaticobiliary ducts within the RSO varies in proportion to the length of the duct L and inversely to the 4th power of its inner diameter d. In other words, to increase the flow resistance of the duct to 2-fold, the length of the duct must be doubled or the inner diameter of the duct must be reduced by approximately 85%. Therefore, the diameter of the CC in the RSO is the factor with the greatest influence on the PBR, and the frequency of contraction and relaxation of the sphincter and the time ratio between contraction and relaxation (duty ratio) also affect the PBR. Our simulation results, shown in Figures 2 & 3, were obtained by assuming a constant CC diameter and varying the CC length. Therefore, the quantities on the horizontal axes of these graphs are proportional to the flow resistance of the pancreaticobiliary duct; that is, the common duct diameter is proportional to the fourth power root of the magnitude of the resistance.

Next, we focus on the right-hand side of Equation 17: The intraduodenal pressure was the back pressure from the pancreaticobiliary system. The instantaneous minimum value of the intraduodenal pressure of a healthy human was almost the same as the intraabdominal pressure. However, the intraduodenal pressure changed transiently due to intestinal peristalsis. If the intraduodenal pressure was higher than the GB pressure without accessory pancreatic ducts in the pancreaticobiliary system, PBR was occur during instantaneous high intraduodenal pressures. Therefore, the differential pressure between the GB pressure and the intraduodenal pressure was one of the significant factors for PBR. As shown in Equation 6, the GB pressure can be determined by the GB compliance, the balance between the inflow rate from the CD and the water-absorption rate at the GB, and the initial GB pressure at the beginning of GB refilling. When the initial intra-GB pressure was low, PBR occurred readily. Therefore, the GB pressure at the beginning of GB refilling was the most influential factor in PBR. GB compliance affects the ratio of the GB pressure increase after meals. If the compliance is low, that is, if the GB becomes stiff, the GB pressure increases rapidly. Therefore, PBR is least likely to occur with a stiffer GB. Compliance of a vessel such as an artery is affected by its volume; the larger the volume, the higher the compliance. Therefore, in addition to the mechanical stiffness of the GB, the size of the GB may also influence PBR. The water-absorption rate at the GB is also an important factor, because it takes longer for the GB pressure to increase when the water-reabsorption rate is high.

Limitations

We were able to demonstrate the influence of the morphological parameters of the pancreaticobiliary ducts on PBR. However, the mathematical model was based on the following three main assumptions: First, we modelled the pancreaticobiliary ducts as straight rigid circular pipes. However, a vortex may occur due to the bifurcation and sudden diameter changes of the pancreaticobiliary ducts. However, the flow resistance caused by the vortex is far less than the resistance of the CC with SO contraction; therefore, its influence on the simulation result is considered to be limited. The compliance of the pancreaticobiliary ducts is also lower than that of the GB; therefore, its effect is also considered to be less significant. Since the compliance of the pancreaticobiliary ducts with dilatation is not negligible, we would like to investigate this in future studies. Second, this study assumed that the mechanical properties, such as viscosity and density, of the bile and pancreatic juices were the same. However, the viscosity of the pancreatic juice and the GB bile was approximately 1.7 and 2.6 times higher than that of hepatic bile, respectively [5,6]. The GB bile filled the CD, CBD, and CC immediately after it was ejected. The viscosity of the working fluid was changed by mixing of the liver bile flow, GB bile flow, and pancreatic juice flow. In our future study, we aim to modify the model by including the changes in viscosity caused by fluid mixing because it is necessary to rigorously simulate not only the fluid flow but also the mass transfer to overcome the aforementioned limitations. Finally, this study neglected the existence of minor pancreaticobiliary ducts such as accessory pancreatic ducts. The influence of such ducts will be studied further in the future.

Conclusion

We investigated the influence of the geometrical parameters of the pancreaticobiliary duct on PBR occurrence using our developed mathematical model for pancreaticobiliary flow based on fluid mechanics theory. The simulation results showed that the flow resistance of the CC within the RSO was a significant factor for PBR regardless of whether the duct was morphologically normal or showed HCPBD or PBM. Our simulations using Fukuzawa’s baseline data setup and our hypothesised CC diameter change due to SO contraction/relaxation indicated that pancreatic reflux appeared when the length of the CC within the RSO was longer than 6 mm when the compliance of the gallbladder was equal to the average value for humans. This result is consistent with the Japanese clinical practice guidelines for PBM. However, the flow resistance of the CC without RSO was completely unaffected. This will enable a more accurate simulation of the flow in the pancreas and bile ducts and allow a quantitative assessment of the effects of differences in the morphology of the pancreas and bile ducts on the flow of bile and pancreatic juice in individual patients.

Acknowledgements

We would like to thank Editage (www.editage.com) for English language editing.

Conflict of Interest

Authors declare no Conflict of Interest for this article.

References

1. Kamisawa T, Amemiya K, Tu Y, Egawa N, Sakaki N, et al. (2002) Clinical significance of a long common channel. Pancreatology 2: 122-128.
2. Kamisawa T, Anjiki H, Egawa N, Kurata M, Honda G, et al. (2008) Diagnosis and clinical implications of pancreatobiliary reflux. World J Gastroenterol 14: 6622-6626.
3. Takuma K, Kamisawa T, Tabata T, Hara S, Kuruma S, et al. (2012) Importance of early diagnosis of pancreaticobiliary maljunction without biliary dilatation. World J Gastroenterol 18: 3409-3414.
4. Sugita R, Furuta A, Yamazaki T, Ito K, Noda Y, et al. (2017) Pancreaticobiliary juice reflux in patients with a morphologically normal ductal system: assessment using unenhanced MRI with spin labeling. AJR Am J Roentgenol 208: 322-327.
5. Ono A, Arizono S, Isoda H, Togashi K (2020) Imaging of pancreaticobiliary maljunction. RadioGraphics 40: 378-392.
6. (1994) The Japanese Study Group on Pancreaticobiliary Maljunction: (JSPBM). The Committee of JSPBM for Diagnostic Criteria; Diagnostic criteria for pancreaticobiliary maljunction. J Hepato-Bil Pancreat Sci 1: 219-221.
7. Kamisawa T, Ando H, Hamada Y, Fujii H, Koshinaga T, et al. (2014) Diagnostic criteria for pancreaticobiliary maljunction 2013. J Hepatobiliary Pancreat Sci 21: 159-161.
8. Hamada Y, Ando H, Kamisawa T, Itoi T, Urushihara N, et al. (2016) Diagnostic criteria for congenital biliary dilatation 2015. J Hepatobiliary Pancreat Sci 23: 342-346.
9. Li W (2021) Biliary tract and gallbladder biomechanical modelling with physiological and clinical elements. Boca Raton: CRC Press.
10. Li WG, Luo XY, Johnson AG, Hill NA, Bird N, et al. (2007) One-Dimensional models of the human biliary system. J Biomech Eng 129: 164-173.
11. Li WG, Luo XY, Chin SB, Hill NA, Johnson AG, et al. (2008) Non-Newtonian bile flow in elastic cystic duct: one- and three-dimensional modeling. Ann Biomed Eng 36: 1893-1908.
12. Al Atabi M, Ooi RC, Luo XY, Chin SB, Bird NC, et al. (2012) Computational analysis of the flow of bile in human cystic duct. Med Eng Phys 34: 1177-1183.
13. Kuchumov A (2018) Biomechanical modelling of bile flow in the biliary system. MATEC Web Conf 145: 04004.
14. Kuchumov A (2019) Patient-specific bile flow simulation to evaluate cholecystectomy outcome. IOP Conf Ser.: Mater Sci Eng 581: 012022.
15. Kuchumov AG, Vedeneev V, Samartsev V, Khairulin A, Ivanov O, et al. (2021) Patient-specific fluid–structure interaction model of bile flow: comparison between 1-way and 2-way algorithms. Comput Methods Biomech Biomed Engin 24: 1693-1717.
16. Fukuzawa H, Kajihara K, Tajikawa T, Aoki K, Ajiki T, et al. (2020) Mechanism of pancreatic juice reflux in pancreaticobiliary maljunction: a fluid dynamics model experiment. J Hepatobiliary Pancreat Sci 27: 265-272.
17. Tajikawa T, Aoki K, Fukuzawa H (2023) Investigation of pancreatic juice reflux mechanism in high confluence of pancreaticobiliary ducts and pancreaticobiliary maljunction (Development and validation of a mathematical model for pancreatic and bile juice flow based on fluid mechanics). J Biorheology 37: 36-43.
18. Cano N, Cicero F, Ranieri F, Martin J, di Costanzo J, et al. (1986) Ultrasonographic study of gallbladder motility during Total Parenteral Nutrition. Gastroenterology 91: 313-317.
19. Ono K (1983) Motility of the sphincter of Oddi and the biliary tract with particular reference to surgical significance of sphincteroplasty. Jpn J Gastroenterological Surg 16: 745-757.
20. Geenen JE, Hogan WJ, Dodds WJ, Stewart ET, Arndorfer RC, et al. (1980) Intraluminal pressure recording from the human sphincter of Oddi. Gastroenterology 78: 317-324.
21. Ethier CR, Simmons CA (2007) Introductory biomechanics from cells to organisms. Cambridge: Cambridge University Press, pp. 180-190.
22. Fung YC (1997) Biomechanics circulation (2^nd).,. New York: Springer, pp. 226-241.
23. Nakayama Y, Boucher RF (1999) Introduction to fluid mechanics. Oxford Press, UK. Butterworth-Heinemann, pp. 118-119.
24. White FM (1994) Fluid mechanics. 3rd ed. Hightstown, New Jersey: McGraw-Hill, pp. 326-327.
25. Middelfart HV, Jensen P, Højgaard L, Funch Jensen P (1998) Pain patterns after distension of the gallbladder in patients with acute cholecystitis. Scand J Gastroenterol 33: 982-987.
26. Kamisawa T, Ando H, Suyama M, Shimada M, Morine Y, et al. (2012) Japanese clinical practice guidelines for pancreaticobiliary maljunction. J Gastroenterol 47: 731-759.
27. Ooi RC, Luo XY, Chin SB, Johnson AG, Bird NC, et al. (2004) The flow of bile in the human cystic duct. J Biomech 37: 1913-1922.
28. Dasgupta D, Stringer MD (2005) Cystic duct and Heister’s “valves”. Clin Anat 18: 81-87.