Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Lakshmi N Sridhar*
Received: November 15, 2023; Published: November 24, 2023
*Corresponding author: Lakshmi N Sridhar, Chemical Engineering Department, University of Puerto Rico, Mayaguez, PR 00681, USA
DOI: 10.26717/BJSTR.2023.53.008470
Bifurcation analysis and optimal control was performed on a model describing the interaction between tumors and macrophages. The MATLAB program MATCONT was used to perform the bifurcation analysis and the optimization language promo is used in conjunction with the state-of-the-art global optimization solvers IPOPT and BARON for the optimal control calculations. Both single and multi-objective nonlinear model predictive control (that involves Multi objective optimal control) calculations were performed. The bifurcation analysis revealed oscillation causing Hopf bifurcations while the optimal control showed the existence of spikes in the control profiles. Both were eliminated using an activation factor involving the hyperbolic tangent function.
Keywords: Bifurcation; Optimization; Control; Macrophage; Tumor
Genetically engineered macrophages that kill tumor cells cause inflammation, leading to DNA and tissue damage. This is remedied by alternatively activated macrophages that can reduce inflammation and repair tissue damage. The interaction between the tumor cells and the two macrophages demonstrates oscillatory behavior that from a mathematical standpoint arises from the existence of a Hopf bifurcation. Oscillations are similar to the existence of spikes in a control profile. Traditionally spikes in optimal control problems are eliminated using a Tanh activation factor. This raises the question of whether using the tanh activation factor will eliminate the unwanted oscillatory behavior that exists because of a Hopf bifurcation. In this work, both bifurcation analysis and optimal control are performed on a scaled dynamic model involving tumor cells and macrophages and it is shown that just as in optimal control, the tanh factor is effective in the elimination of spikes, it also eliminates the Hopf bifurcation that causes oscillatory behavior.
Mantovani and co-workers [1-3] studied tumor immunity, macrophage polarization, and the effect of Macrophage immunity on cancer. Wilke and Hahnfeldtt [4] developed a model studying the dichotomy of the immune response to cancer: Rakoff-Nahoum [5] studied the interaction between cancer and inflammation Prehn [6] studied investigated the effect of the immune reaction on the as a stimulator of tumor growth. Sica and co-workers [7] investigated Macrophage polarization in tumor progression. The two macrophages’ phenotypes are divided into M1 and M2 macrophages. M1 cells have anti-tumor properties that can produce pro-inflammatory cytokines to eradicate pathogens but can cause tissue and DNA damage. M2 cells can reduce the pro-inflammatory response and stimulate tissue repair. Allavena and Mantovani [8] suggested a re-polarization of macrophages towards the classically activated M1 cells, as an effective treatment approach to ensure tumor elimination. A considerable amount of computational work has been done dealing with tumor macrophage interactions. As early as 1985, De Boer, et al. [9] presented a model of the interactions between macrophages and T lymphocytes that generate an anti-tumor immune response. Owen and Sherratt [10] developed a five-dimensional differential equations model to study the roles of macrophages presence, influx, and ability to selectively kill tumor cells in avascular tumors. They verified that the proportion of macrophages in tumors increases with the chemotactic activity of the mutant cell line. Byrne, et al. [11] proposed a mathematical model that describes the interactions between normal cells, tumor cells and infiltrating macrophages, to evaluate the ability of the engineered macrophages to eliminate the tumor changes as model parameters vary Owen, et al. [12] investigated the role of chemotaxis, chemokine production and the efficacy of macrophages as vehicles for drug delivery to hypoxic tumor sites.
Webb, et al. [13] extended the model of Owen [12] to show that limited-diffusivity or non-cell- cycle dependent drugs help macrophages effectively target hypoxic tumor cells. Eftimie [14-16] studied the complex dynamics in the interactions between the macrophages and tumor cells. Dong, et al. [17] and Ghosh [18] and Liu, et al. [19] show that the models describing the dynamics of macrophage and tumor interactions exhibit periodic oscillations which indicate the presence of Hopf bifurcations. Shu, et al. [20] show the existence of Hopf bifurcations in the model describing the interaction between tumor cells, M1 and M2 macrophages. Sridhar [21] showed that the use of the hyperbolic tangent activation factor was effective in removing spikes in a control profile. Repeated spikes are similar to oscillatory behavior and the aim of this paper is to use a similar hyperbolic tangent activation factor on the tumor macrophage interaction model and demonstrate that the oscillation causing Hopf bifurcation can be eliminated. This paper is organized as follows. First, the tumor macrophage interaction model Shu, et al. [20] is described. This is followed by a discussion of the bifurcation analysis and the multi-objective nonlinear model predictive control strategy that involves optimal control. The results are then presented and discussed followed by conclusions.
Tumor Macrophage Interaction Model
The model and its scaled version Shu, et al. [20] is presented in this section. The model includes three variables: the population of tumor cells (T), the population of M1 macrophages (M1) and the population of M2 macrophages (M2). The interactions among these three cells is described by the following differential equations:

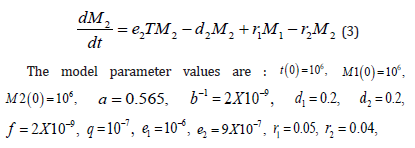
Owing to the large variation of parameters convergence for bifurcation analysis and optimal control is difficult. Hence a scaled model

Bifurcation Analysis
There has been a lot of work in chemical engineering involving bifurcation analysis throughout the years, The existence of multiple steady-states and oscillatory behavior in chemical processes has led to a lot of computational and analytical work to explain the causes for these nonlinear phenomena. Multiple steady states are caused by the existence of branch and limit points while oscillatory behavior is caused by the existence of Hopf bifurcations points. In the case of branch points and limit points the Jacobian matrix of the set of steadystate equations is singular. However, at a branch point, there are 2 distinct tangents at the singular point while at a limit point, there is only one tangent at the singular point. Singularities in the Jacobian matrix is often indicative of an optimal solution, and this motivates the investigation of how the singular points in the Jacobian matrix, indicated by branch and limit points would affect the multi-objective dynamic optimization. One of the most used software to locate limit points, branch points, and Hopf bifurcation points is MATCONT Dhooge, et al. [22,23]. This software detects Limit points, branch points and Hopfbifurcation points. Consider an ODE system:

for both limit and branch point the matrix B must be singular. For
a limit point (LP) the n +1th component of the tangent vector 1 0 n v + =
and for a branch point (BP) the matrix 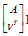 must be singular. For a Hopf
bifurcation, the function should be zero. indicates the biternate
product while n I is the n-square identity matrix. More details can be
found in Kuznetsov [24,25] and Govaerts [26]. The PI has published
several articles where bifurcation analysis was used in chemical engineering
problems such as reactive distillation and fermentation Ruiz,
et al. [27-30]. Hopf bifurcation points cause unwanted oscillatory behavior
which makes control tasks difficult.
must be singular. For a Hopf
bifurcation, the function should be zero. indicates the biternate
product while n I is the n-square identity matrix. More details can be
found in Kuznetsov [24,25] and Govaerts [26]. The PI has published
several articles where bifurcation analysis was used in chemical engineering
problems such as reactive distillation and fermentation Ruiz,
et al. [27-30]. Hopf bifurcation points cause unwanted oscillatory behavior
which makes control tasks difficult.
Multi-Objective Nonlinear Model Predictive Control (MNLMPC) Method
The multi-objective nonlinear model predictive control (MNLMPC) method was first proposed by Flores Tlacuahuaz, et al. [31] and used by Sridhar [32-36]. This method is rigorous, and it does not involve the use of weighting functions do not do it impose additional parameters or additional constraints on the problem unlike the weighted function or the epsilon correction method (Miettinen; 1999). For a problem that is posed as

The MNLMPC method first solves dynamic optimization problems independently minimizing/maximizing each xi individually. The minimization/maximization of xi will lead to the values * xi Then the optimization problem that will be solved is:
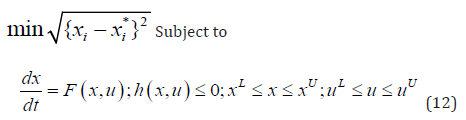
This is the MOOC calculation. It will provide the control values for various times. The first obtained control value is implemented and the remaining discarded. This procedure is repeated until the implemented and the first obtained control value are the same. The optimization package in Python, Pyomo Hart, et al. [37] where the differential equations are automatically converted to a Nonlinear Program (NLP) using the orthogonal collocation method Biegler, [38] is commonly used for these calculations. The state-of-the-art solvers like IPOPT Wachter and Biegler [39] and BARON Tawaralmani and Sahinidis [40] are normally used in conjunction with PYOMO. To summarize the steps of the algorithm are as follows.
1. Minimize/maximize i x subject to the differential and algebraic
equations that govern the process using Pyomo and Baron.
This will lead to the value xi*
2. Minimizemin  (multi-objective function) subject to
the differential and algebraic equations that govern the process.
This is the MOOC calculation and provides the control
values for various times. If this calculation results in obtaining
a value of zero for the multi-objective function, then the
Utopia point is obtained, and the cal
(multi-objective function) subject to
the differential and algebraic equations that govern the process.
This is the MOOC calculation and provides the control
values for various times. If this calculation results in obtaining
a value of zero for the multi-objective function, then the
Utopia point is obtained, and the cal
culations are terminated.
Otherwise, we proceed to step 3.
3. Implement the first obtained control values and discard the
remaining.
4. Repeat steps 1 to 3 until there is an insignificant difference
between the implemented and the first obtained value of the
control variables.
5. This strategy was used in Sridhar [30-34].
First, the bifurcation analysis was performed on a scaled model
describing the tumor macrophage interactions. As shown by Shu
[20], the model exhibits Hopf bifurcations when ζ is the bifurcation
parameter. However, when the activation factor tanh (ζ )
ε
is introduced
and the resulting bifurcation parameter is ζ tanh (ζ )/
ε
the Hopf bifurcation
point disappears. ε is taken as 10−3 .Such an activation factor
is commonly used to control spikes or miniature waves in optimal
control problems. Figures 1a & 1b show the two profiles with and
without the activation factor tanh (ζ )
ε
. It can be seen that the use of
the activation factor eliminated the Hopf bifurcation point. Figures 2a
& 2b show the optimal control profiles for the single objective optimal control is performed minimizing ζ versus time minimizing the
scaled variable X subject to the equations 4 5 and 6. The resulting
value of the objective function is 8e-05. However, the control profile
exhibits a spike as seen in Figure 2a. When the activation factor is
used the spikes disappear as seen in Figure 1b. Using this corrected
value of ζ Oscillatory behavior is like the existence of spikes, and it
is shown that the activation factor involving the tanh function is effective
in eliminating both and this is the main message in this article.
The Multi-Objective Nonlinear Model Predictive Control (MNLMPC)
calculations were also performed. First, X was minimized while Y and
Z were maximized individually [41-43]. The objective function values
obtained are 0.0109, 8.95 and 2.156. The objective function for the
MNLMPC calculations is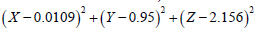 subject to
the scaled differential equations. The first obtained control value of
value of x was implemented and the process is repeated until there
is no difference between the first obtained control value and the implemented
control value. In this case tis value is 0.0292. Figures 3-6
show the profiles of the various variables where MNLMPC was used.
subject to
the scaled differential equations. The first obtained control value of
value of x was implemented and the process is repeated until there
is no difference between the first obtained control value and the implemented
control value. In this case tis value is 0.0292. Figures 3-6
show the profiles of the various variables where MNLMPC was used.
Bifurcation analysis and optimal control was performed on a scaled model involving interactions between macrophages and tumors. Oscillation causing Hopf bifurcation points were found. It is shown that the incorporation of the hyperbolic tangent function (Tanh) that is normally used to eliminate spikes in optimal control profiles is also effective in the elimination of the unwanted oscillation causing Hopf bifurcation points.
All data used is presented on paper.
The author, Dr. Lakshmi N Sridhar, has no conflict of interest.


