Determining When Subscale Scores from Assessment Measures Provide Added Value Volume 53- Issue 5

Walter P Vispoel*, Hyeryung Lee and Tingting Chen

• Department of Psychological and Quantitative Foundations, University of Iowa, USA

Received: November 10, 2023;   Published: November 16, 2023

*Corresponding author: Walter P Vispoel, Department of Psychological and Quantitative Foundations, University of Iowa, USA

DOI: 10.26717/BJSTR.2023.53.008457

Abstract PDF

In this brief article, we describe methods that can be effectively used to determine the value of reporting subscale in addition to composite scores from assessment measures, illustrate additional techniques to determine the number of items needed to support the viability of subscale scores, and direct readers to resources where relevant formulas and computer code are provided to implement these procedures.

Researchers and practitioners routinely use measures that produce scores at different levels of aggregation. Common examples of such measures include achievement batteries that produce total scores and nested sub-scores for separate subject matter areas (e.g., English, reading, math, science; [1]), ability inventories that produce both total scores and nested sub-scores for different areas of intellectual functioning (e.g., verbal, quantitative, non-verbal; [2]), personality questionnaires that include scores for both global domains (e.g., neuroticism) and more specific subdomain facets nested within each domain (e.g., anxiety, angry hostility, depression, self-consciousness, impulsiveness, vulnerability under neuroticism; [3]), and so forth. An important question often asked about subdomain or subscale scores from such measures is whether they provide useful information or added value beyond the total or composite scores reported for those instruments. To answer this question, measurement specialists have produced a variety of indices to quantify subscale viability. In this article, we illustrate one such procedure first described by Haberman (2008, [4], also see [5-7]) that can encompass a wide variety of measurement paradigms including classical test theory, generalizability theory, item response theory, and factor analytic techniques [8-12].

Haberman (2008)’s method is based on computation of indices for a subscale and its associated composite reflecting reduction in measurement-related error when estimating the underlying construct( s) represented by the subscale’s scores. Technically, the indices for the subscale and composite reflect proportional reductions in mean-squared error (PRMSE, [4-12]) when estimating true scores from observed scores. These indices, in turn, can then be used to create a value-added ratio (VAR; see [7]) by dividing the PRMSE for the subscale by the PRMSE for the composite scores as shown in Equation (1). VAR values greater than 1.00 would support reporting subscale in addition to composite scores, and increasingly so as VARs deviate further away from 1.00.

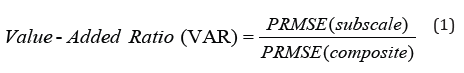
In illustrations to follow, we use data from a study by (Vispoel, et al. [13]) to apply and extend Haberman’s method to the measurement of personality traits. The data consists of responses from 330 college students who completed the recently updated and extended 60-item form of the Big Five Inventory (BFI-2 [14]). The BFI-2 measures five superordinate personality traits (Agreeableness, Conscientiousness, Extraversion, Negative Emotionality, and Open-Mindedness), along with three nested subordinate constructs or facets for each superordinate trait (see (Table 1) for titles for all facet subscales). Within the reported analyses, composites and subscales respectively represent superordinate and subordinate constructs. Composite scales have twelve items, with four items for each of three nested subscales that are equally balanced for positive and negative phrasing. Items are answered using a 5-point Likert-style rating scale (1 = Disagree strongly, 2 = Disagree a little, 3 = Neutral, no opinion, 4 = Agree a little, and 5 = Agree strongly)

Table 1:

The second column in (Table 1) shows VARs for all BFI-2 subscales in their original form with four items per subscale. The results reveal that nine of the fifteen subscale scores (Organization, Assertiveness, Energy Level, Sociability, Depression, Emotional Volatility, Aesthetic Sensitivity, Creative Imagination, and Intellectual Curiosity) provide evidence of added value beyond associated composite scores. Such results would then beg a logical follow-up question concerning how the remaining subscales might be revised to reach the threshold for added value.

A useful way to address this problem is to apply generalizability theory-based prophecy techniques [15-19] to determine the extent to which increases in numbers of items might improve subscale added value (see [8-12] for further details). The remaining columns (3-6) in (Table 1) include estimates of VARs for each subscale when pairs of items are successively added up to a maximum of 12 total items. The results show that the threshold for VARs exceeding 1.00 to support subscale score viability is reached by adding four more items to the Trust, Productiveness, and Anxiety subscales. However, this threshold is not met for the Compassion, Respectfulness, and Responsibility subscales even after adding eight more items, thereby highlighting the redundancy of those subscales with their domain composite scores. To reach the desired threshold for these subscales and avoid inclusion of an excessive number of items, the original items might be revised to overlap less with other subscales within the same global personality domain.

The examples just described illustrate the value of using Haberman’s procedure coupled with generalizability theory prophecy techniques to evaluate the benefits for reporting subscale in addition to composite scores from a popular measure widely used in psychological research. However, these techniques are applicable to any assessment domain and instrument for which both composite and subscale scores are reported. Additional information about Haberman’s methods can be found in [4-12], and formulas and computer code for integrating them with generalizability theory techniques are provided by Vispoel and colleagues [20-23]. We hope that readers will familiarize themselves with these procedures to improve the quality and efficiency of measurement procedures in relevant areas of personal interest.

1. ACT, inc. (2022) ACT® Technical Manual. Iowa City, IA, ACT, inc.
2. Lohman DF (2012) Cognitive Abilities Test, Form 7: Research and development guide. Rolling Meadows, IL: Riverside.
3. McCrae RR, Costa PT (2010) NEO Inventories professional manual. Lutz, FL: Psychological Assessment Resources.
4. Haberman SJ (2008) When can subscores have value? Journal of Educational and Behavioral Statistics 33(2): 204-229.
5. Haberman SJ, Sinharay S (2010) Reporting of subscores using multidimensional item response theory. Psychometrika 75(2): 209-227.
6. Sinharay S (2019) Added value of subscores and hypothesis testing. Journal of Educational and Behavioral Statistics 44(1): 25-44.
7. Feinberg RA, Wainer H (2014) A simple equation to predict a subscore’s value. Educational Measurement: Issues and Practice, 33(3): 55-56.
8. Vispoel WP, Lee H (2023) Merging generalizability theory and bifactor modeling to improve psychological assessments. Psychology and Psychotherapy: Review Study 7: 1-4.
9. Vispoel WP, Lee H, Chen T, Hong H (2023a) Analyzing and comparing univariate, multivariate, and bifactor generalizability designs for hierarchically structured personality traits. Journal of Personality Assessment pp: 1-16.
10. Vispoel WP, Lee H, Chen T, Hong H (2023b) Extending applications of generalizability theory-based bifactor model designs. Psych 5(2): 545-575.
11. Vispoel WP, Lee H, Hong H (2023a) Analyzing multivariate generalizability theory designs for psychological assessments within structural equation modeling frameworks [Teacher’s corner]. Structural Equation Modeling: A Multidisciplinary Journal pp: 1-19.
12. Vispoel WP, Lee H, Hong H, Chen T (2023a) Applying multivariate generalizability theory to psychological assessments. Psychological Methods pp: 1-23.
13. Vispoel WP, Lee H, Xu G, Hong H (2023) Integrating bifactor models into a generalizability theory based structural equation modeling framework. Journal of Experimental Education 91(4): 718-738.
14. Soto CJ, John OP (2017) The next Big Five Inventory (BFI-2): Developing and accessing a hierarchical model with 15 facets to enhance bandwidth, fidelity, and predictive power. Journal of Personality and Social Psychology 113(1): 117-143.
15. Cronbach LJ, Rajaratnam N, Gleser GC (1963) Theory of generalizability: A liberalization of reliability theory. British Journal of Statistical Psychology 16(2): 137-163.
16. Cronbach LJ, Gleser GC, Nanda H, Rajaratnam N (1972) The dependability of behavioral measurements: Theory of generalizability for scores and profiles. New York NY: Wiley.
17. Shavelson RJ, Webb NM (1991) Generalizability theory: A primer. Sage.
18. Brennan RL (2001) Generalizability theory. New York, NY: Springer-Verlag.
19. Vispoel WP, Morris CA, Kilinc M (2018) Applications of generalizability theory and their relations to classical test theory and structural equation modeling. Psychological Methods 23(1): 1-26.
20. Vispoel WP, Lee H, Chen T, Hong H (2023c) Instructional online supplement to “Analyzing and comparing univariate, multivariate, and bifactor generalizability designs for hierarchically structured personality traits.” Journal of Personality Assessment pp: 1-29.
21. Vispoel WP, Lee H, Chen T, Hong H (2023d) Instructional online supplement to “Extending applications of generalizability theory-based bifactor model designs.” Psych 5(2): 1-29.