info@biomedres.us
+1 (502) 904-2126
One Westbrook Corporate Center, Suite 300, Westchester, IL 60154, USA
Site Map
ISSN: 2574 -1241
ISSN: 2574 -1241
Received: October 10, 2023; Published: November 03, 2023
*Corresponding author: Töysa T, Licentiate of Medicine, Specialty General Practice, Retired, Student of Eastern Finland, Kuopio, Finland
DOI: 10.26717/BJSTR.2023.53.008424
Introduction: In a Finland, environmental factors, i.e., variables (V), {(Mg/Ca), and (Mg/K) ratios in estimated total fertilization and Mg content of soil (Mgs)}, have shown significant correlations with coronary heart disease (CHD) among different Finnish population subgroups {female (F)and male (M), in rural (rur) and urban (urb) regions}. Discrepancy between correlations needed clarification. This article compares associations between CHD’s and a Mgs predictor, E.Mgs (attained by combined regression of Mgs by Mg/Ca, and Mg/K) as well as associations between their proportional deviations (Vpd) from their exponential trendlines (Ve). (Ve) for years Yi, (α≤ i≤ω): POWER(10,k*(Yi - Yα))*Vα; k = log10(Vω)- log10(Vα). (Vpd) = (V - Ve)/Ve* Mutual correlations were computed between native variables (CHD’s and E.Mgs) and separately between their (Vpd)’s, mutually.
Results: Original E.Mgs explained CHD’s inversely on an average 58.4 % (range: 8.3 - 78.4). (E.Mgs.pd) explained (CHD.pd)’s, even inversely, by 58.1 % (range: 53.3 - 61.6), (p < 0.001). CHD’s explained each other on an average by 40.5 % (range: 12.9 - 60.6), respectively (CHD.pde)’s by 87 % (range: 84.1 - 91.3), (p < 0.001). Beta coefficient of (Mg/K) was stronger (+1.3) than by (Mg/Ca) (-0.4). V.pd formation harmonized statistical “dependent variables” (CHD subgroup’s) making possibly “explaining” in this case more reliable.
Conclusions: It seems possible that fertilization ratios influenced on Finnish agricultural soil Mg level and inversely to CHD variation. Changing variables to proportional deviations from exponential trendlines reduced discrepancy between “dependent factors” (CHD subgroup’s) and seemed to ease “explaining” by environmental factors (variables).
Keywords: Mg; Soil; Fertilization; Heart; Fertilizer Ratios; Mg/Ca; Mg/K; Statistical Analysis; Proportional Deviation from Exponential Trendline.
Abbreviations: α: The First One (e.g. of the Years); Beta Coefficient: A Measure of Relative Power of Factors in SD Units; “.AL”: (Post-Suffix) Soil Value Attained by Ammonium Lactate Method; CHD: Coronary Heart Disease; “e”, Small e (Post-Suffix): Exponential Trendline; E, Big E (Pre-Suffix) in “E.(Mgs)”: Expected Mgs by Combined Regression by Approximate Fertilization Ratios (in 3 Year Means) of (Mg/Ca) and (Mg/K)”;. F (Pre-Suffix): Female; F1 = Mg/Ca Fertilization Ratio; F2 = Mg/K Fertilization Ratio; [F1,F2]: Combined Regression by F1 and F2; Mgs: Mg.sm: (Soluble - Exchangeable) Mg Concentration of Soil; pd: Proportional Deviation from Exponential Trendline, (Vpd) = (V -Ve)/Ve*100; R2: R Square of the Regression, (“Explaining Measure”); “.rur”: “.r”: Rural; sm: (in (Table 1). Mean Value of all Collected Samples During 5-year period), Soil Value, when there is no Need of Space, e.g. (Mg/Ca).sm; “.urb”: “.u”: Urban; V Variable (Factor) Selected to Replace F (Reserved for Females); ω: The Last One; ( ), Parentheses: for Strengthening or Separating
In a Finland, environmental factors, i.e. variables (V), {(Mg/Ca), and (Mg/K) ratios in estimated total fertilization and Mg content of soil (Mgs)}, have shown significant correlations with coronary heart disease (CHD) among different Finnish population subgroups {female (F) and male (M), in rural (rur) and urban (urb) regions [1,2]}. These fertilization factors (F1) and (F2) and Mgs explained CHD often stronger than single behavioral factors [1,2], but not without discrepancy. This as physiological data [1,3] support the role of Mg (especially Mg deficiency) on metabolic risks in cardiac system. In soil Ca, Mg and K influence on each other: relative increase in one of them in soil reduces the content of others in plant. K has the highest ability in these replacement phenomena [4]. In plants deficient Mg can be replaced by other cations (obviously especially in monocots?) so that K content can rise to 3-fold to the physiological needs of plants, and produce visible Mg deficiency in plants, although soil content of Mg is sufficient [4,5]. Soil Mg Table 1 has explained male CHD by 98 % (p < 0.001) during 1961-90 [6]. The aim of this study is to try find an estimate for Mg.sm values, Mgs. Predictor, for total period 1952-86, by fertilizers and examine its associations with CHD directly and with V.pd formations.
Table 1: Main cations of Finnish agricultural soils, 1961-90.
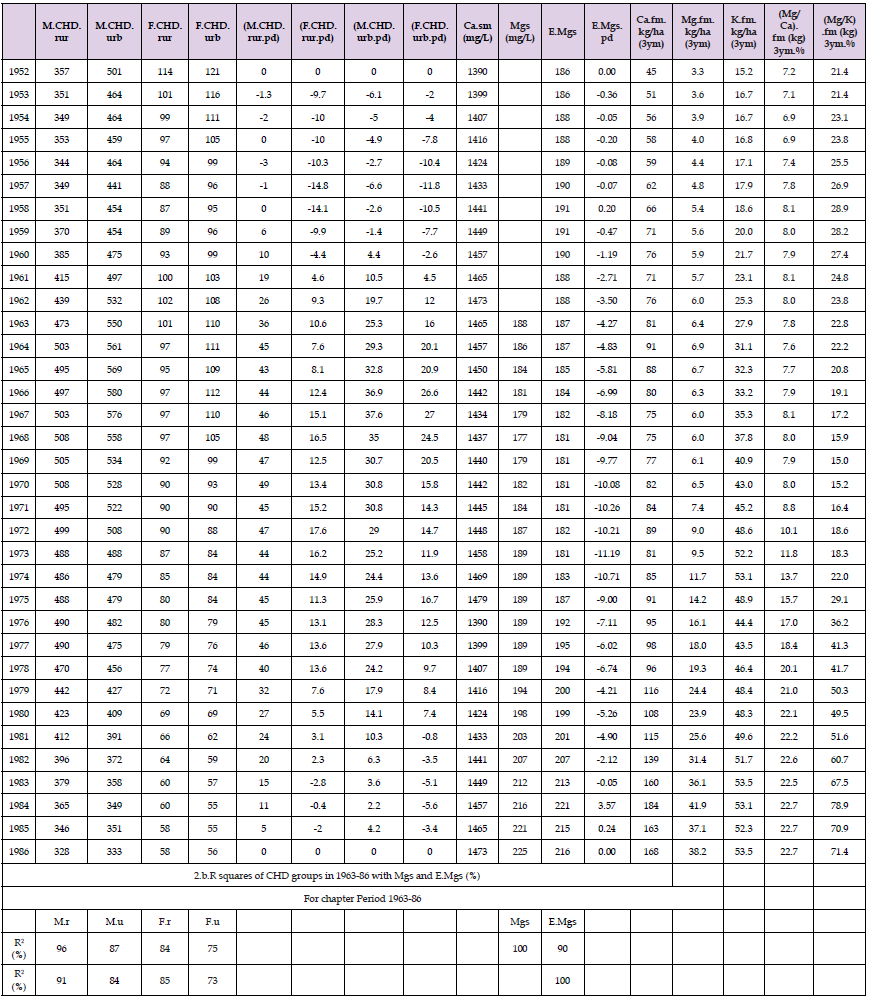
Material of this study are attained from [1,2]: (age-adjusted) CHD mortality amongst rural [rur] and urban [urb] males [M] and females [F] in 1952-86. Data is readily given by 3-year means. Soil data are from the same sources as in [1]. All soil values are given in Table 1, because in [1] values of Mg were given in mg/L, others in equivalents. Annual soil estimates are attained by linear interpolation (Table 2). Because the data concerning recycled mineral elements of recycled nutrients are inconsistent, total fertilization [1] is replaced here by the amounts of “commercial”, “inorganic”, “mineral” fertilizers (fm), by kg/ha, that people who are interested on soil science could compare and rejuvenate the given Finnish data. The aim of unit selection is to help orientation with soil chemistry, where values are given by weight units. N.B. Ca.fm and Mg.fm (estimates) are including Ca and Mg from liming agents “fm”. To change Mg/K kg-ratio to equivalent ratios need multiplying by 1.65, Mg/K respectively by 3.22. Fertilizer data are given by kg/ha, as 3-year means (rolling averages), (3ym).
In Figure 1 and Figure 2 represent formation of exponential trendlines Ve and proportional deviation from the exponential trendlines, Vpd. Figure 1 shows formation of the exponential trendline Ve (M.CHD.urb.e) for periods 1952-86 and 1963-86. Variable values for years Yi, (α≤ i≤ω): POWER(10,k*(Yi-Yα))*Vα; k = log10(Vω)- log10(Vα). Figure 2 shows annual proportional deviation from exponential trendline, Vpd (M.CHD.urb.pd) = (V-Ve)/Ve*100 (in percent). Figure 2 shows (M.CHD.urb.pd)’s, differences between M.CHD.urb and its exponential trendline (M.CHD.urb.e) – in percent in two periods. (M.CHD.rur.pd) formation means “horizontalization” of the time-axis. Vertical distances between M.CHD.urb and (M.CHD.urb.e) from Figure 1 stay vertical. By regression of soil Mg (1963-86) by (Mg/Ca). fm and (Mg/K) fm are attained E.Mgs.(63-86), i.e. [EMg.sm.(63-86)], constant and coefficients, by which are computed estimates for E.Mgs. (52-86), E.Mgs.(52-86).e and E.Mgs.(52-86).pd (Figure 3). The aim of this study is to assess associations of CHD subgroups with soil Mg predictor, E.Mgs, by using native factors (V) or by replacing them by (V.pd)’s. Visual analyses are performed additionally by proportional values of parameters relative to their values in 1958 “, (i/58)”. Results (x) are given by R2 in percent (“explaining” percents”). Calculations are made by MS Exel and IBM SPSS programs.
Table 2: Shows data on CHD’s, (CHD.pde)’s, Mg.sm, E.Mg.sm and E.(Mg.sm.pde) (CHD.pde)’s, E.Mg.sm and (E.Mg.sm.pde) are precalculated.
Figure 1
Figure 2
Figure 3
Visual Representation of the Data
Figure 4 shows male CHD in rural and urban regions in 1952-86, with soil Mg and soil Mg predictor Figure 5 shows female CHD in rural and urban regions in 1952-86, with soil Mg and “soil Mg predictor” (E.Mgs.E.fm. checked data)) Figure 6 shows development of male and female CHD in rural and urban regions and the exceptionality of M.CHD.rur to the 3 other CHD subgroups.
Figure 4
Figure 5
Figure 6
Period 1963-86 Shortly
Combined regression of Mg.sm by (Mg/Ca).fm and (Mg/K).fm (fertilization) factors, i.e. E.Mgs, explained Mgs by 90 % (p < 0.001), as it is seen in Figures 4 & 5 (especially, if we cut the Fig’s at 1963). Unstandardized “coefficients” of this regression were: constant 174, coefficient for (Mg/Ca): -0.59; for (Mg/K) +0.77. Absolute value of beta (by standard deviation standardized) coefficient for (Mg/Ca) was (-0.28) and for (Mg/K) +1.20, 4-fold to the respective value of (Mg/Ca). Mgs and E.Mgs explained CHD’s nearly equally (by 75-96 % and 73-91 %, respectively. Associations were higher in rural and male groups than in respective other groups. V.pd formation are not calculated here for this period (Table 2).
Period 1952-86 – Native Factors
Associations between Native Factors: E.Mgs explained CHD variation on an average by 61 % (range: 30 - 78) (Table 3). No order within males and females: Highest association with urban males, lowest with rural males, within females rural group had the highest association. Reciprocal variation of CHD subgroups was explained on an average by 48 % (range: 3-96), respectively. M.CHD. rur explained F.CHD. rur by 5 % (p = 0.22) and F.CHD.urb by 3 % (p = 0.32), non-significantly. Other associations were highly significant, even in E.Mgs association with M.CHD. (30 %) significance level was very high: p < 0.001. As an example is represented regression of F.CHD. rur by M. CHD.rur (Figure 7). It explained F.CHD. rur variation by 4.6 %. Figure 7 shows Regression of F.CHD. rur by M. CHD.rur. Regression explained F.CHD. rur by 5 % (p = 0.215).
Table 3: R squares (R2) between CHD’s and E. Mgs cum means.
Figure 7
Period 1952-86 Assessed by V.pd Factors
(E.Mgs.pd)’s explained (CHD.pd) variation by 76 % (range: 68 - 83) (Table 4). Associations were highest between males. In male and female groups associations were highest in rural regions. (CHD.pd) subgroups explained reciprocal variation on an average by ca 87 % (range: 79 - 95). Significance level: p < 0.001, by all. Associations were in general higher than in Table 3, e. g. association between rural females and males was 88 % (Table 4 & Figure 8), respective association by native values was 5 % (Table 3 & Figure 7). The reciprocal association between males was higher than between females, opposite to Table 3. Figure 8 Regression of F.CHD.rur. pd by M.CHD. rur.pd explained F.CHD. rur. pd by 88.1 % (p < 0.001 (as in all cases, in which R2 > 30 %).
Table 4: R squares (R2) between (CHD. pd)’s and (E.Mgs.pd) cum means.
Figure 8
Figure 9 shows CHD’s and E.Mgs in pd-formation (on different scales) and their inverse time-related association.
Figure 9
Results are the same as in Table 4. Figure 10 (M.CHD.rur.pd) was explained 83 % by (E.Mgs. pd). (Figure 11). (F.CHD.rur.pd) was explained 83 % by (E.Mgs.pd). Figure 12 (M.CHD.urb.pd) was explained 83 % by (E.Mgs.pd). Figure 13 (F.CHD.urb.pd) was explained 83 % by (E.Mgs.pd). Figures suggests that (E.Mgs.pd) explains (CHD.pd), (CHD.pd)’s are preceding (E.Mgs.pd).
Figure 10
Figure 11
Figure 12
Figure 13
Hidden Mg deficiency: In a preliminary study (1950-55) [4] Heinonen concluded that the annual Mg loss from Finnish agricultural soils was about 10 kg/ha. About 5 kg of that could be replaced by manure, because Finnish farms are (were) mainly dairy cattle farms. 2 kg of the losses could be replaced by dolomitic nitro chalk since 1957, when its production was beginning in Oulu, in a new Finnish fertilizer factory, by replacing Ca(NO3)2. Mg supply could rise to 10 kg/ha via high (reasonable) doses of nitro chalk. Generally it is known, that the planned replacements of Mg did not occur: The number of cattle farms was reduced (exact data is difficult to find) and other N-fertilizers replaced dolomitic nitro chalk. Heinonen wanted to continue his study, but it was not supplied, because “Mg balance for the whole country was not found to be showing a loss” [6]. Soil Mg associated negatively with grain and ley yield [6]. Mg supplementation seemed to be rarely beneficial: Mg supplementation did increase yield only “at really low soil Mg” concentration level [6]. Decrease in soil (Mg/K) ratio so that Mg content of grain decreased from 1.1 to 0.7 mg/kg (air dry grain of barley) increased the grain yield [7]! This observation seemed to be so unbelievable that it was not in English summary of [7].
(Comment: K excess of soil behaved like a growth stimulant, causing “obesity of grain”, remarkable that the study plant, barley was monocot, as obviously in [6], which are the main sources of Finnish food and feed). Mg fertilization of monocots cannot increase their Mg content to ideal level for cattle feeding [6]. Ideal fodder needs dicots, e. g. clover. Clover, the source of Mg [6] as well as vegetables, can suffer from Mg deficiency without visible signs, although they have enough Mg for chlorophyl production [4]. Mg is important for several biological processes, e. g. biological nitrogen combining (Zimmerman 1947, Bear 1951 in [4]). This was unknown in 1968, when poor success of clover was discussed [8] and represented that strong N-fertilization of monocots can replace the protein of clover. When soil data are available only since 1961, this work tries to explain CHD risk by fertilizer factors during 1952-86, by the model how they explain Mg.sm in 1963-86. Another aim was to find factors which are the same for males and females and changes are simultaneous with CHD’s. Big problem was: how to explain the inverse association of M.CHD.rur with F.CHD’s in period 1952-77 (can be calculated by data in Table 2), in order they could be explained by the same environmental factors. This discrepancy is clarified to some extend by “parameters of proportional deviation from exponential trendlines”, V.pd formations.
This problem was caused by the S-shape of the CHD curves.Equation of E.Mgs.(63-86){combined regression of Mgs by fertilization ratios of (Mg/Ca).fm and (Mg/K).fm}, which explained 90 % of soil Mg (Mgs) and CHD nearly as well (Table 2) in 1963-86, its constant and coefficients The constant and coefficients for 1963-86 were benefited for formation of E.Mgs.(52-86). [E.Mgs.(52-86)] explained CHD variation, in different population groups on an average by 61 % (range 30-78), p < 0.001 within each group. As it was supposed from earlier publications [4,5], the effect of soil K could be stronger and more dynamic to change plant Mg than that of Ca. In combined regression by Mg.sm by (Mg/Ca).fm, and (Mg/K).fm beta coefficient for (Mg/Ca).fm (1) was ca -0.28 and (2) for (Mg/K).fm +1.2 (SD-units). Figure 14 represents the regression of Mg.sm (E.Mgs) and its formation: Constant, Constant + Coeff.(1) x (Mg/Ca).fm and, Constant + (Mg/K).fm. Figure 15 shows by the regression coefficients of Mg.sm regression by (Mg/ Ca).fm and (Mg/K).fm in 1963-86 computed E.Mgs, with its components for 1952-86: Constant, Constant + Coeff.(1) x (Mg/Ca), Coeff. (2) x (Mg/K).fm. This equation can explain even the decrease of CHD mortality in 1952-57, when simultaneously Mg/Ca decreased and Mg/K increased (not discussed in [9]) The relative fertilization changes at about 1958 show the timepoint of the begin of decreasing Mg availability simultaneously with increase in CHD mortality. (Accuracy of fertilization data before 1961 [10] is open for revisions).Proportional variation from the exponential trendline (E.Mgs.pd) between the start point (α) and endpoint (ω), Figure 3 explained respective CHD variation, (CHD.pd)’s, by 76 % (range: 68 - 83), respectively (Table 4). CHD’s explained reciprocal variation by 48 % (range: 3 - 96).
Figure 14
Figure 15
(CHD.pd)’s explained reciprocal variation by 87 % (range: 79 – 95). These ratios include complicated hidden factors: Because K.fm was mainly given as a part of complex fertilizers, variation of K.fm explained ca 99.0 % of the variation in NP.fm [(N+P).fm] fertilization [10]. The changes in P and N fertilization in general fortified reduction in Mg availability in long term, although the effect of N-fertilizers could in a short term be Mg output increasing [6]. The most dramatic worsening in Mg deficiency syndromes occurred since radical increase in N-fertilization in 1968 [8,11,12]. Magnesium deficiency increased psychic and psychiatric symptoms [11,12]. Clinical picture of grass tetany is like that of Delirium tremens. Increase in total fertilization can increase leaching of cations in general [4], but in acid soils Ca can reduce leaching of Mg [4]. Increase in Ca fertilization via liming agents could have changed (by neutral ammonium acetate) extractable Mg to non-extractable form according [6], but according Jerlström [7] could have reduced the transfer of Mg from non-extractable (by ammonium lactate, ”AL”) to extractable form without change in soil Mg. The role of extractable and non-extractable Mg (reserve-Mg), as well as silicon need another article. The Figures 4 & 5 explain more realistically the changes in CHD mortality than Figure 6. Male and female CHD mortality was lower in rural than in urban regions until 1971-73.
This can be explained by the hard work in forests and farms. In 1965 the estimate of an average energy supply was 4200 kcal for farmers [13]. Similarity in rural and urban CHD mortality after 1972 can possibly show/be explained as the end of “well-being” disease. Remarkable is that this article is treating time-related data, as if Finnish mixture of soils were at one point, where concentrations are observed between 5-year intervals, although they are collected gradually, with unknown frequency. In this data Pearson correlation of [E.(Mg/Ca). sm with E.Mg.sm)] is 0.997 and by original values [(Mg/Ca).sm with Mg.sm)]: 0.974. Inter-areal coincidental association of soil Mg and (Mg/Ca) was much lower and dependent on fertilization and soil-type distribution [14]. Predicting weights of different environmental factors (V) is very difficult, if depending factors have discrepancies (Table 3 & Figure 7). (V.pd) formation harmonized statistical “dependent factors” (CHD subgroup’s) (Table 4 & Figure 8) and seemed to open a new way to measure parallelism. Anyhow in period 1963-86 CHD’s (not readily calculated) were better explained by E.Mgs than CHD. pd’s by E.Mgs.pd. Better explanation in 1952-86 can be explained by S-shape of the mortality curve.It is obvious that in Finland there was a dietary epidemic of Mg deficiency [1], partially dependent on rapidly changed fertilization with consequences in human (CHD) and animal health. PubMed Search: “(proportional) deviation from exponential trendline” retrieved zero results.
Equation of combined regression of Mg.sm by fertilization factors (Mg/K) and (Mg/Ca) explained highly significantly inversely CHD mortality in four Finnish population groups in 1963-86. The same equation explained variation of CHD in 1952-86 and determined its epidemical start to ca 1958. Associations strengthened and became more coherent after replacement of original variables to proportional deviations from their exponential trendlines, Vpd. Vpd seems to be an instrument for assessment of parallelism, its general benefits are to be seen.
I am grateful to late Osmo Hanninen and Seppo Haaranen for co-working during many years and to Tapani Valkonen for pre-thinking and permission to his printed charts, as well as to Eurofins for permission to use their big data.
Abstract
PDF
