A Further Examination of Excesses or Deficits of
Terminal Zeroes in Scientific Research: Using Binomial
Testing to Assess Probabilities for Different Anomaly
Classifications as a Function of Different Sample Sizes
of Coefficients with Terminal Digits

Walter R Schumm

doi:10.26717/BJSTR.2023.52.008293

Short CommunicationOpen Access

A Further Examination of Excesses or Deficits of Terminal Zeroes in Scientific Research: Using Binomial Testing to Assess Probabilities for Different Anomaly Classifications as a Function of Different Sample Sizes of Coefficients with Terminal Digits Volume 52- Issue 4

Walter R Schumm*

Department of Applied Human Sciences, Kansas State University, USA

Received: August 19, 2023; Published: September 06, 2023

*Corresponding author: Walter R Schumm, Department of Applied Human Sciences, Kansas State University, 1700 Anderson Avenue, Manhattan, KS, USA

DOI: 10.26717/BJSTR.2023.52.008293

Abstract PDF

ABSTRACT

One feature recognized as a possible indication of fraudulent research is a deficit or excess of zeroes as terminal digits, compared to an expected rate of ten percent, in coefficients reported for regression and standard error coefficients. Some have translated various percentages of zeroes as terminal digits into an anomaly measure (e.g., fewer than three percent or more than twenty percent of zeroes as terminal digits might be classified as a “major” anomaly while 3.01 to 5.00% or 15.00 to 19.99% might be classified as a “moderate” anomaly). However, it has not been clear if such ordinal classifications have any meaning in terms of probability or statistical significance. The probability levels of various anomaly levels are presented and illustrated by an analysis of terminal zeroes in 16 research articles published by Dr. Eric Stewart, who has been accused of fabrication of data or results in several of his scientific publications. It is unlikely to find low probability levels (< .05) for coefficient samples of less than 50 cases but moderate or major anomalies usually have low probabilities for samples of more than 50 to 100 cases. In the case of Dr. Stewart, more than a dozen of his published articles featured probabilities below 5% with respect to zeroes as terminal digits. Using percentage classifications to create an anomaly measure for terminal digits appears to be useful when cases exceed fifty or sixty.

Introduction

There are many ways to try to detect if research has been manipulated or fabricated [1,2]. In some cases, probability formulas can assist in such efforts [3]. An excess or deficit of terminal digits in regression coefficients and their standard errors may signal data manipulation or even fabrication [4,5] because terminal digits should be approximately random (i.e., zero would occur about 10% of the time). Recently, Dr. Eric Stewart has been accused of fabricating his data or results [6-8] and was fired from his position as a full professor at Florida State University in March 2023. One of the factors involved in detecting anomalies in his publications was a frequent deficit or excess of zeroes as terminal digits in his results [9-11] where anomalies in terminal digits were classified by percentage; major anomaly (3% or fewer zeroes or 20% or more zeroes, moderate anomaly (3.01-5.00% or 15% to 19.99%), or slight anomaly (5.01 to 6.99% or 13.01 to 14.99%). The advantage of classification by percentage is that, regardless of the number of coefficients involved, the same standard can be applied to all articles in question. However, it is probable that with very small samples of coefficients, percentage-based classifications might yield anomaly classifications that were not statistically significant.

Objectives

First, binomial tests will be used to assess the validity of percentage- based anomaly classifications for different sample sizes of coefficients with terminal digits. Second, anomaly classifications assigned to articles authored by Dr. Stewart will be tested to determine how many might have been misclassified.

Methods

The most obvious issue with terminal digits that do not end in zero would be when there were no digits ending in zero or perhaps only one or two at most. But under what sample sizes (of coefficients) would such small numbers be lower than the expected ten percent and to also be statistically significant at levels of p < .05 or p < .10? Since the expected probability of a random digit is ten percent and since terminal digits in regression/standard error coefficients are approximately random, binomial tests can be used to assess the probabilities of given levels of occurrence of terminal digits. Here the focus will be on zeroes as terminal digits since such zeroes appear to be associated with fabricated research [4,5] and have been common in Dr. Stewart’s research [9-11]. Specifically, if we have 50 or any other number of coefficients, we can use binomial tests to calculate the probability of obtaining any number of zeroes or range of zeroes as terminal digits.

Using binomial tests [www.socscistatistics/tests/binomial/default2. aspx], it is apparent that 0 terminal digits of zero out of 29 or more cases/coefficients would be significant (p < .05) or 0/22 or more close to significant (p < .10). Likewise, combinations of 1/46 and 1/38 or 2/61 and 2/52 will yield similar levels of probability. At the same time, a ratio of 0/20 might seem unusual, but it would not be statistically significant. Anomaly levels created as ordinal measures to assess indications of possibly fabricated data or results will be evaluated for coefficient sample sizes of 100, 200, 300, and 500. Sixteen articles by Dr. Eric Stewart that were assigned moderate or major anomaly levels because of unusual patterns of terminal digit zeroes will be re-evaluated in terms of probability levels.

Results

What would the significance levels be for the classifications used by Schumm and his colleagues [9-11] for different sample sizes of coefficients evaluated? In (Table 1), results are provided for unusually low percentages of terminal digits ending in zero, for sample sizes of coefficients of 100, 200, 300, and 500. In (Table 2), results are provided for unusually high percentages of terminal digits ending in zero, for sample sizes of coefficients of 100, 200, 300, or 500 (Table 3). Schumm and his colleagues used a range of 7-13% to represent a normal level of terminal digit zeroes. Was that accurate? For n = 100, 200, 300, and 500 the probability of an outcome falling in that range are, respectively, .60, .80, .90, and .97. In all four examples, a majority of the time, the expected outcome was within the range of 7-13%.

Table 1: Probabilities associated with lower than expected percentages of zeroes as terminal digits.

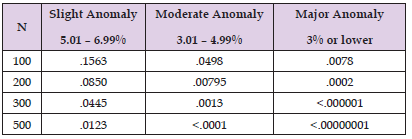
Table 2: Probabilities associated with higher than expected percentages of zeroes as terminal digits.

Table 3: Classifications of Stewart Publications with Moderate to Major Anomalies for Terminal Digits and Associated Significance Levels.

Discussion

Even with a lack of zeroes as terminal digits, a sample of coefficients must be at least of 29 tests to yield a probability below .05. With one or two zeroes, samples of 46 or 61 coefficients, respectively, are needed for a probability below .05. For samples of 100, major anomalies, as defined by Schumm et al. [6-8], would have probabilities < .01, while moderate anomalies would have probabilities < .05. For samples of 300 coefficients, slight anomalies would have probabilities < .05. Approximately, levels of anomalies correspond to their statistical probabilities. As a practical illustration, articles by Stewart and his colleagues that had 40 or more coefficients and had been rated as having moderate or major anomalies with respect to zeroes as terminal digits also featured probabilities below .05, while those articles with fewer than 35 coefficients usually featured probabilities > .05 even if rated as having moderate or major anomalies with respect to zeroes as terminal digits.

In conclusion, for samples with more than 50 coefficients that can be tested for terminal digits, ratings of moderate to major anomalies appear to make statistical sense. For samples of 200 or more coefficients, even ratings for slight anomalies will feature relevant trends, with probabilities below .10, even below .05 for samples of 300 or more coefficients. These results can help future researchers more quickly evaluate apparent discrepancies in percentages of terminal digits, especially in terms of zeroes as terminal digits. While some of the anomaly classifications used by Schumm and his colleagues [7-9] for evaluating Stewart’s research did not feature probabilities below .05, it may be reasonable to consider a nearly complete lack of terminal zeroes as an issue of concern, even when not significant, in the context of numerous articles with far larger samples of coefficients that also featured few, if any, or large excesses of terminal zeroes.

If a scholar publishes large numbers of articles in which there are unusual percentages of zeroes as terminal digits (either too many or too few compared to the expected ten percent) even articles with [6- 11] so few cases as to be of only moderate probabilities may contribute to an overall pattern of anomalies in terms of zeroes as terminal digits. Probabilities associated with lower or higher than expected percentages of zeroes as terminal digits are one among other indications of anomalies that might signal scientific misconduct, even fabrication of data or results [12-27].