A Decision Support System for Modelling Wildlife Corridors in India Volume 52- Issue 1

Saurabh Shanu* and Alok Agarwal

• School of Computer Science and Engineering, University of Petroleum and Energy Studies, India

Received: July 27, 2023;   Published: August 07, 2023

*Corresponding author: Saurabh Shanu, School of Computer Science and Engineering, University of Petroleum and Energy Studies, Dehradun 248007, Uttarakhand, India

DOI: 10.26717/BJSTR.2023.52.008196

Abstract PDF

Wildlife corridors are landscape elements that allow species and processes to flow freely across sections of intact habitat, connecting the ecosystems within the landscapes. Thus, in a particular environment, the areas that link the scattered habitat patches are known as corridors. The main goal of creating conservation corridors is to counter and, to the extent possible, mitigate the effects of habitat loss and fragmentation on the biodiversity of the landscape, as well as to support the continuation of land use for vital local and international economic activities in reference. In this study, a network of wildlife corridors with the tiger (Panthera tigris tigris) as the focus species using game theory, graph theory, membership functions, and chain coding algorithm is modelled and designed. To create a graph that represents the habitat patches that support tiger presence in the landscape complex as vertices and potential routes between them as edges, initially the parameters that would impact the tiger population in the landscape complex are explored. Tigers are treated as individual players in the Assurance game that has been used to plan the transit of tigers via potential pathways. The tiger moves across each grid that has been taken into consideration for the model when the game is played iteratively. The iteration causes the tiger to choose the most suitable path signifying the emergence of adaptability.

Keywords: Landscape Complex; Corridor; Assurance Game; Graph Theory; Chain Code Algorithm; Finite Deterministic Automata

The degree to which the environment allows for transit across resource habitat patches is known as landscape connectivity [1,2]. A corridor is defined as an area, typically linear and enclosed in a matrix within a landscape, that connects two or more habitat patches, thereby establishing a link between the habitats, and that is intended for conservation on the grounds that it will enhance or maintain the passage of key wildlife populations in the concerned habitat patches. Additionally, a technique for route selection as the movement of individuals of the target species through a corridor from one habitat patch to another is defined through the work [3]. As mentioned by the statement above, wildlife corridors are essential elements of ecological landscapes. Wildlife corridors are designed to make it easier for processes and creatures to flow across regions of the landscape that are under consideration. Thus, in a particular environment, corridors are areas that often contain native vegetation and connect other isolated and fragmented animal habitat patches [3,4]. The two main groups of components that make up corridors, which are essential parts of landscapes, are pattern components and process components [4]. The categories of wildlife corridors are shown by the structural and functional functionalities. The functional corridor is a product of both the species and the landscape, and the structural categorization relates to the geographical presence of the landscape between the focal patches.

Therefore, a functioning wildlife corridor relates to both a notion peculiar to a species and a landscape. As a result, corridors may be seen as developing phenomena that are brought about by interactions between local processes and pattern features. By facilitating the movement of both biotic and abiotic processes, wildlife corridors ensure gene flow between spatially separate populations of species that have become fragmented due to landscape changes [4-7]. This is the fundamental purpose and utility of wildlife corridors. Researchers have demonstrated that presence of species-specific wildlife corridors within a given landscape to be instrumental in increasing gene flow and population sizes of the species [6,7-10]. The considerations suggest that any accurate modelling to create wildlife corridors must be a species-specific endeavor, with a suitable habitat selection for the relevant target species. The present work outlines a computational process for creating a corridor for the Tiger (Panthera Tigris Tigris). The relative spatial location of national reserves in relation to one another proves to be a crucial consideration when making resource allocation decisions for a biogeographically diverse and vast country like India. This can either protect existing tiger corridors or, in some cases, even create proper wildlife corridors.

Therefore, choosing the critical tiger habitats (CTH) in such a decision- support model must take into account how their spatial structure ensures a high degree of interconnectedness within the heavily human-dominated landscapes, throughout the course of a long-term land-use scenario. Designing the connectivity among the current (or even possible) habitats or CTH using a network model would be one way to accomplish the goal. Each tiger habitat in such a network would be considered a vertex, and the tiger corridors connecting these vertices would be the edges. This paper’s main goal is to present a fundamental computational architecture for comprehending a workable corridor network design inside the focal landscape complex for tigers. The basic notion of connectedness, according to which the presence and feasibility of a corridor must be recognized and totally decided by the landscape characteristics and structure, is the center of all arguments and observations in this study. The planning and designing of tiger corridors within the terrain is defined as a connectivity subgraph problem [3]. The conflict between the travelling tiger and the terrain characteristics brought about mostly by human activity is then included via an assurance game. Further, the work demonstrates an optimized way and utilize these optimized paths to create a Deterministic Finite Automata to produce the language for creating corridors, which may be asserted as a rule foundation for corridor design after being aware of the potential costs.

The current work is mostly semi-empirical and schematic in form, despite references to a landscape map of the focal complex. However, the proposed model is of the opinion that the work could serve as a schema for an informed decision-making by conservationists and wildlife managers when designing real-world corridors because it focuses on the presence or absence of corridors linking various tiger habitats in the complex, the distances involved, and the ease of movement for the tiger through these corridors. Section 2 contains the essentials of the mathematical concepts that have been used in this paper. Sections 3 and 4 describe the modelling and the conclusion of the work, respectively.

In the current study, a modelling technique for a tiger-friendly wildlife corridor that makes use of a few key computational frameworks is proposed. To make the task self-contained, the essential concepts of these frameworks are explained in this part. Game theory has been utilized to simulate the impact of the presence or absence of certain factors in a grid on the selection of tigers for migration. The choice of tigers for movement is essentially random, but computationally, what must be preferred in accordance with the tigers’ behavioral pattern has been described here, which might serve as an active approach for creating the corridors. The consequences of the significant non-linear computational interactions between the parameters and the focal species are essentially what the results are. The current situation is best portrayed by the assurance game. When simulating the current interactions, it is assumed that the focal species and the set of parameters are participants in the game and so accumulate a sequence of pay-offs concentrating on both the co-players and their own tactics.

To create the intricate interdependence of parameters impacting the focus species, the game is recursively replayed across discrete time-steps. Additionally, in the Assurance game, each participant must always invest a little amount of resource if they want to benefit from the strategy they have selected. Because such games accurately represent the behaviors, particularly with relation to the biological communities, they would therefore best capture the flavor of coordinated, evolutionary games [11-14]. We assume that each iteration of the game involves the participants sharing processed data to construct a workable interactions model for further tiger moves. Each interacting tiger receives a countable quantity of data from the contributing factor as an input at each discrete time step at a specific state, and at the following discrete time step, it transitions to an unambiguously determined next state. To describe the movement of the focal species, a finite deterministic automaton is designed based on this supposition [15-17]. It is also proposed that a regular language derived from automata may be used to understand how corridors work in terms of exchanging information. Considering the aforementioned arguments, the following research question has been formulated: What are the finite deterministic automata and the transition rule/ language that simulate the creation of wildlife corridors in the Indian landscape?

Let G(Θ,Σ,Π) be a normal form, strategic game where ∀i∈I = {1,..., n}⊂ℵ, n ≥ 2 , (i) 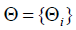is the set of interacting agents or players;

(iii) Π :Σ→ℜ i is the payoff function, which assigns to each strategy profile σ a real number Π (σ) i , the payoff earned by the player i Θ when is played in n Π = Π ×...×Π 1 . is the space of payoff functions in the game.

profile. To comprehend the interactions between the parameters and Tiger that result in the building of corridors in a landscape, the assurance game is employed. To analyze this n-player Assurance game, the pay-off matrix from [18] has been utilized as follows: (Table 1) The rewards that each participant receives for working and interacting together are represented by the matrix. The payoff matrix made it clear that a player’s reward from a strategy depended on the proportion of players in the population that play C or D. The payoffs for players who are playing C change monotonically as more players cooperate within the parameters. On the other hand, regardless of the number of players that choose to defect, the player’s scoring while employing the Defection strategy stays constant.

Table 1: n-Player Assurance payoff matrix.

The factor by which each parameter in the input space is transferred to a membership value (or degree of membership) between 0 and 1 is described by a membership function (MF), which is a degree value curve. The whole grid area that would be considered for the landscape serves as the input space for the current modelling.

A linked series of pixels is used to depict an edge using chain code [19]. According to (Figures 1a & 1b) this representation often relies on 4 (or) 8 connections between the segments. Each segment’s direction is coded using a numbered system (Figure 1).

Figure 1

For the purpose of the present work, we assume that the tiger habitat patches in India constitute the vertices and the collection of connections within this complex that connect any two of the habitats constitute the edges, comprising the focal landscape complex as a graph (V, E,ψ ) Γ Γ [20]. The existence of an edge between any two vertices represents some ecological flux, such as animal movement, between the adjacent vertices. We first identify a set of landscape factors or parameters, which may be natural or anthropogenic and each of which may either constrain or support the passage of the tiger through the focal landscape matrix to various degrees, and hence become the main determinants in the structural connections becoming a corridor, in order to model the possible paths to serve as passages for tigers from one habitat patch to another habitat patch within any considered landscape complex. For describing the present model, [21] we consider five parameters a, b, c, d and e. We assume that tigers in the landscape and the set of above mentioned parameters of the landscape constitute the two rational agents that play the Assurance game [22] iterated over a number of generations. The players may use a number of strategies in the game in order to optimize their payoff.

Table 2: Coding for the tiger habitats in the complex.

These payoffs are the costs incurred by the tiger population (called tiger henceforth in the paper) in using the landscape matrix for movement between habitats. These benefits are offset by the expenses the tiger population (hence referred to as the tiger in the research) incurs when using the landscape matrix to travel across habitats. Next we code the different tiger habitats [23] included in the focal landscape complex, by the following (Table 2): In order to explain the model we create a random landscape image as shown in (Figure 2) (Table 1) and the map in (Figure 2) lead to an adjacency matrix , i = 1,2,..., n; j = 1,2,..., n , where n = 4 for tiger habitat patches, which can be seen in (Table 3) and visualized through (Figure 3 & Table 3). We can verify that there is communication between each patch using the adjacency matrix we acquired, but the key is to choose the link that would allow the passage of tigers with the least amount of loss [24]. The expenses incurred by tigers in exploiting the links between various habitat patches in the given landscape complex are then computed in order to determine such a path.

Figure 2

Figure 3

Table 3: Adjacency matrix A=[aij] for tiger habitats in the sample landscape complex.

We further develop the Assurance game model incorporating the contribution of each grid component while computing the cost matrix. Due to its existence or absence, each landscape element influences the cost matrix. We take into account five criteria for the current model, [25] and we categorize them as indicated in (Table 4).

Table 4: Factor categorization and score contribution.

For the purpose of scoring, we make few assumptions for our model, which can be perfectly calculated once worked on with the Remote Sensing and GIS data. The assumptions made are:
1. The area of each grid in the landscape is constant = A.
2. The area occupied by a factor f in a grid Gij denotes the membership of the factor in the considered grid and is given by: μ_f/Gij = A_f/Gij / A
3. The score of each parameter in a grid is based on its categorization and then application of bilinear interpolation between the values considered. For e.g. if then

Table 5: Cost matrixes of the tiger for using existing corridors between different habitat patches in the complex.

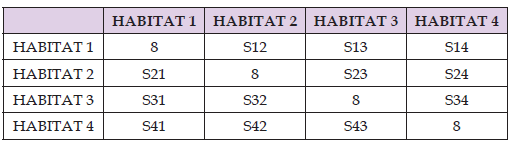
Based on the above criteria of scoring, the various factors with respect to tiger using the membership of each factor in each grid and the strategy space [26-28] of Assurance game the following cost matrix is obtained (Table 5). For the present theoretical modelling we assume the following order of the scores, which can be correctly obtained using the presence, absence and abundance data of Remote Sensing and GIS:

Using the above scores, we can rank the grids using the chain code algorithm which can be seen as: (Figure 4) Let the DFA that models the corridor designing and improving the landscape conditions for supporting movement of tigers be M (Q,Σ, q,δ , h) . We list the objects comprising M in the following paragraphs:
Q comprises the following set of states, representing the different states of grids that the tiger encounters while moving through it:
• Initial State(I)
• Not fovourable state(NFS)
• Fairly fovourable state(FFS)
• Moderately fovourable state(MFS)
• Fovourable state(FS)

Figure 4

The set of symbols also termed as alphabet Σ = {a, b, c, d, e} includes the letters (inputs for the automata), that happen to be the parameters present in the grid to play G.
I is the initial state, describing the initial state of a grid which appears as the tigers move out from the territorial region. The transition function δ is explained by the following matrix: (Table 6)

Table 6: Transitions of Δ to various states.

There exist two states which may be included in the state of final states which are:
• NFS: Not Favorable for movement of tigers and thus cannot be supported or converted to corridor due to massive interferences from inhibitory sources.
• FS: Favorable State for movement, as it supports the movement of tigers through them with highest priority. There exist two states which may be included in the state of final states which are:
• NFS: Not Favorable for movement of tigers and thus cannot be supported or converted to corridor due to massive interferences from inhibitory sources.
• FS: Favorable State for movement, as it supports the movement of tigers through them with highest priority (Figure 5).

Figure 5

The above Automaton would generate a regular grammar (CFG), which would, in essence, be obtained by the transition function δ. Let the non-terminals in the DFA are denoted by Y. Y comprises the following states:
• I: Initial State (I)
• J: Not favorable state (NFS)
• K: Fairly favorable state (FFS)
• L: Moderately favorable state (MFS)
• M: Favorable state (FS)
Corresponding to such a set of non-terminal states, the context free grammar (CFG) could be written as:
→ I→ cJ|aK|cL|Dm|eK
*J→ cJ|aK|cL|dM|eK
K→ cJ|aK|cL|dM|eK
L→ cJ|aK|cL|dM|eK
*M→ cJ|aK|cL|dM|eK
J, M is the final state of the automata, which, for the sake of identification, is prefixed by an asterisk sign.

The current work was created with the following goals:

(i) Obtain a rule set to design a workable tiger corridor network, connecting the tiger habitat patches in the landscape complex using a repeatable [29-34] computational procedure; and

(ii) Identify the most crucial habitat patches, along with their underlying community structure, in order to concentrate conservation efforts on them.

In this study, we employed deterministic finite automata to create a language that may be used as a template for creating actual tiger corridors in the Indian landscape. The designing of the corridor is entirely based on the structural definition of connectivity, and as a result, some critically important landscape features, such as the biotic factors of the availability of prey [35-40] base and water, are not taken into account when computing the cost matrix, which is a limitation of the modelling described in the paper. By design, the work is kept simple to offer a foundational computational architecture for visualizing a [41,42] workable structural corridor network design in the primary tiger habitat complex. Due to two factors—first, our paper prioritized path efficiency over repetitions, and second, the work focuses on estimating the best connecting strategies for the CTHs rather than taking into account alternate paths—we may be able to justify this omission of path redundancy consideration [43-47]. We are aware that such simplification frequently does not correspond to the circumstances of a genuine corridor. However, we anticipate that our current work would provide a computational framework for building tiger corridors, which may undoubtedly be enhanced by including field data from realistic considerations.

1. Taylor PD, Fahrig L, Kimberly A (2006) Landscape connectivity: A return to the basics. In: Connectivity conservation, Crooks, KR & Sanjayan M (Eds.)., p. 29-43.
2. Urban DL, Keitt TH (2001) Landscape connectivity: A graph-theoretic perspective. Ecology 82: 1205-1218.
3. Beier P, Noss RF (1998) Do habitat corridors provide connectivity? Conservation Biology 12(6): 1241-1252.
4. Chetkiewicz B CL, St Clair CC, Boyce MS (2006) Corridors for conservation: Integrating pattern and process. Annu Rev Ecol Evol Syst 37: 317-342.
5. Beier P, Loe S (1992) A checklist for evaluating impacts to wildlife movement corridors. Wildlife Society Bulletin 20: 434 -440.
6. Dutta T, Sharma S, Maldonado JE, Wood TC, Panwar HS, et al. (2013) Gene flow and evolutionary history of leopards (panthera pardus) in central Indian highlands. Evolutionary Applications.
7. Hanski I (1998) Metapopulation dynamics. Nature 396: 41-49.
8. Hanski I, Gilpin M (1991) Metapopulation dynamics – brief-history and conceptual domain. Biol Journal of the Linnean Society 42: 3-16.
9. Hanski I, Ovaskainen O (2000) The metapopulation capacity of a fragmented landscape. Nature 404: 755-758.
10. Harris LD, Gallagher PB (1989) New initiatives for wildlife conservation: The need for movement corridors. In Preserving Communities and Corridors G Mackintosh Defenders of Wildlife Washington DC p. 96.
11. Nowak MA, Sigmund K (1983) Chaos and the evolution of cooperation Proc Natl Acad Sci USA 90: 5091-5094.
12. Nowak MA, Bonhoeffer S, May RM (1994) Spatial games and maintenance of cooperation Proc Natl Acad Sci USA 91: 4877-4881.
13. Minor ES, Urban DL (2008) A graph-theory framework for evaluating landscape connectivity and conservation planning. Conservation Biol 22(2): 297-307.
14. Rayfield B, Fortin MJ, Fall A (2011) Connectivity for conservation: A framework to classify network measures. Ecology 92(4): 847-858.
15. Hofbauer J, Sigmund K (1998) Evolutionary Games and Population Dynamics. Cambridge University Press Cambridge. Addison Wesley (2006).
16. Baland JM, Platteau JP (1996) Halting Degradation of Natural Resources. Oxford University Press.
17. Dunne JA, Williams RJ, Martinez ND (2002) Network structure and biodiversity loss in food webs: robustness increases with connectance. Ecological Lett 5: 558-567.
18. Hofstadter DR, G del (2000) Escher Bach: an Eternal Golden Braid Penguin.
19. Hopcroft JE, Motwani R, Ullman JD. Introduction to Automata Theory Languages and Computation.
20. Axelrod R, Hamilton WD (1981) The evolution of cooperation. Science 211: 1390-1396.
21. Axelrod R (1984) The Evolution of Cooperation. Basic Books Inc New York.
22. Baum KA, Haynes KJ, Dillemuth FP, Cronin JT (2004) The matrix enhances the effectiveness of corridors and stepping stones. Ecology 85(10): 2671-2676.
23. Bonacich (1972) Factoring and weighting approaches to status scores and clique identification. Journal of Mathematical Sociology 2(1): 113-120.
24. Bondy J, Murty USR (2008) Graph Theory. Springer New Delhi.
25. Bunn AG, Urban DL, Keitt TH (2000) Landscape connectivity: A conservation application of graph theory. Jour Environ Manag 59: 265-278.
26. Cantwell MD, Forman RTT (1993) Landscape graphs; ecological modelling with graph-theory to detect configurations common to diverse landscapes. Landscape Ecol 8: 239-255.
27. Digital Image Processing (2^nd )., by Gonzalez and Woods Pearson Publications.
28. Fall A, Fortin MJ, Manseau M, O Brien D (2007) Spatial graphs: Principles and applications for habitat connectivity. Ecosystems 10: 448-461.
29. Gopal R, Qureshi Q, Bhardwaj M, Singh RKJ, Jhala YV (2010) Evaluating the status of the endangered tiger Panthera tigris and its prey in Panna Tiger Reserve. Madhya Pradesh India Oryx 44: 383-398.
30. Jhala YV, Gopal R, Qureshi Q (Eds.) (2008) Status of Tigers, Co-predators and Prey in India. National Tiger Conservation Authority Govt. of India New Delhi and Wildlife Institute of India Dehradun TR08/001 Pp. 151.
31. Jhala YV, Qureshi Q, Gopal R, Sinha PR (Eds.) (2011) Status of Tigers, Co-predators and Prey in India. 2010. National Tiger Conservation Authority Govt of India New Delhi and Wildlife Institute of India Dehradun. TR2011/003 Pp. 302.
32. Levett WJM (2008) an Introduction to the Theory of Formal Languages and Automata. John Benjamins.
33. Jordan F, Liu WC, Davis AJ (2006) Topological keystone species: Measures of positional importance in food webs. Oikos 112: 535 - 546.
34. Keitt TH (2003) Network theory: An evolving approach to landscape conservation. In Ecological Modelling for Resource Management Dale VH (ed) Springer New York Pp.125-134.
35. Kruskal JB Jr (1956) On the shortest spanning subtree of a graph and the travelling salesman problem. Proc Amer Math Soc 7 (1): 48-50.
36. Nowak MA, Sigmund KA. strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner’s Dilemma game 364(6432): 56-58.
37. Opdam P, Verboom J, Powels R (2003) Landscape cohesion: An index for the conservation potential of landscapes for biodiversity. Landscape Ecology 18: 113-126.
38. Opdam P, Steingrover E, van Rooij S (2006) Ecological networks: A spatial concept for multi-actor planning of sustainable landscapes. Landscapes and Urban Planning 75: 322-332.
39. Ozgur A, Vu T, Erkan G, Radev DR (2008) Identifying gene-disease associations using centrality on a literature mined gene-interaction network. Bioinformatics 24(13): i277-i285.
40. Santos M, Szathmary E (2009) The evolution of cooperation Treballs de la SCB 60: 213-229.
41. Pulliam HR (1988) Sources, sinks and population regulation. American Naturalist 132: 652-661.
42. Taylor PD, Fahrig L, Henein K, Merriam G (1993) Connectivity is a vital element of landscape structure. Oikos 68: 571-573.
43. Urban DL, Minor ES, Treml EA, Schick S (2009) Graph models of habitat mosaics. Ecology Lett 12: 260-273.
44. Webb JN (2007) Game Theory: Decisions, Interactions and Evolution. Springer New Delhi.
45. Wikramanayake ED, Dinerstein E, Robinson JG, Karanth U, Rabinowitz A, et al. (1998) An ecology based method for defining priorities for large mammal conservation: the tiger as case study. Conservation Biol 12(4): 865-878.
46. Wikramanayake E, McKnight M, Dinerstein E, Joshi A, Gurung B, et al. (2004) Designing a conservation landscape for tiger in human-dominated environments. Conservation Biol 18(3): 839-844.
47. Yumnam B, Jhala YD, Qureshi Q, Maldonado JE, Gopal R, et al. (2014) Prioritizing tiger conservation through landscape genetics and habitat linkages. PLoS ONE 9(11): e111207.