The Biophysical Modelling of the Osmosis in the Living Systems Volume 51- Issue 2

Janos Vincze* and Gabriella Vincze Tiszay

• Health Human International Environment Foundation, Hungary

Received: June 16, 2023;   Published: June 23, 2023

*Corresponding author: Pragyan Roy, Department of Biotechnology, College of Basic Science and Humanities, OUAT, Bhubaneswar 751003, India

DOI: 10.26717/BJSTR.2023.51.006053

Abstract PDF

The transport phenomena mean the variation in time and space of generalized forces when they generate flows for which conservation laws apply. This general and strongly scientific definition of the transportation phenomena has two major merits:

1. Particular forms of transportation can be deducted from it (mass transport – diffusion; energy transport – thermal conductibility; impulse transport – viscosity; task / load transport – electric conductibility, crossed effects and other)

2. It allows a quantitative characterization of the product exchange, which was impossible based on the previous definitions.

If W – the amount of the transported parameter, for which the conservation law is valid; K – a constant dependent on the type of transportation and the nature of the transported parameter; grad a – the generalized force, then the amount of the parameter (flow) transported through the surface dS in the dt time frame will be given by the relation:

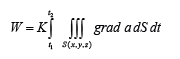
The various compartments of the living organisms are separated from one another through membranes with selective permeability. Between two solutions of various concentrations of the same solvent, separated through a membrane impermeable for the solvent, the migration of the solvent takes place from the diluted solution in the concentrated one. This phenomenon is called osmosis. We observe that osmosis is a particular case of diffusion. If on a part of the semipermeable membrane there is pure solvent and on the other side a solution of this solvent, then the molar concentration of the solvent in the first compartment will be C₁ = 1, and in the second one it will be:

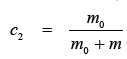
where: m0 – number of solvent molls in the volume unit; m – number of the molls of the substance dissolved from the same volume. Since c₁>c₂, according to the laws of diffusion, the solvent will pass from the first compartment to the second one where its concentration is lower [1]. Following the movement of the solvent from the point of view of the solvate, this being the parameter we are measuring, we can state that the osmotic flow always passes from the more diluted solution towards the most concentrated. The solvent diffuses until the equalising of the existing hydrostatic pressure.

The necessary pressure for preventing osmosis is called osmotic pressure, whose value is calculated on the van’t Hoff’s law:

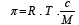
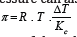
Knowing this, we can review the osmosis laws: all the solutions of the same concentration, at equal temperatures, have the same osmotic pressure; at constant temperature, the osmotic pressure is directly proportional with the value of the solution’s concentration; when the concentration is constant, the osmotic pressure varies directly proportional with temperature. The osmosis is frequently found in the living organisms, due to the numerous semipermeable membranes between the various compartments. The walls of the capillaries, for example, act like such a membrane placed between blood and the interstitial liquid. If the osmotic pressure of a solution coincides with the one of the blood plasma, we talk about an isotonic solution. The osmotic pressure of the isotonic solutions is equal to the one of the blood plasma, the one of the hypotonic solution is lower and the osmotic pressure of the hypertonic solutions is higher than the plasma’s. If the plasma is diluted with a hypotonic solution, the red cells swell osmotically with water, until (in the virtue of the osmosis laws) they break (they lyse). In hypertonic solutions, the red cells loose water and they shrivel. In both cases the red cell’s functionality is compromised.

If a semipermeable membrane interposes between two solutions with different molarity (n1 and n2) the osmotic pressure will be: π = (n1 – n2) RT. On equal concentrations, there is no osmotic pressure. When an external pressure (P) is exerted on the solution different from the osmotic pressure (π), then for P > π the solvent flow goes from the solution towards the solvent and for P<π the solvent flow will have a different direction. This phenomenon lies at the basis of the capillary exchanges: at the arterial end of the capillaries the blood’s hydrostatic pressure is higher then to the osmotic one and the substances pass in the interstitia; at the venous end the osmotic pressure is lower then to the osmotic one and the substances pass in the blood [2]. In the case of osmosis, the generalized force is the pressure gradient, which generates a volume flow. The characteristic parameter of the process is the osmotic pressure (π). By making the necessary replacements in the general equation of the transport processes, we obtain the relation:

Sometimes, we find the notion of osmotic mechanical work (L). It shows that in the case of existence of an osmotic pressure π, due to which a substance is transported through a membrane which separates the two compartments, an osmotic mechanical work is performed. When the two solutions of various concentrations (c1 < c2) are separated through a membrane permeable only for the solvent, this will cross the membrane towards the most concentrated solution, until a difference of hydrostatic pressure equal to osmotic pressure π = p appears. In this case the system itself performed an osmotic mechanical work (L), whose expression can be deducted in the following mode:

Using the osmosis law, we obtain for osmotic mechanical work:

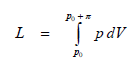
The osmosis laws apply only in certain dilutions:

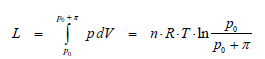
in the case of very high or very low concentrations of dissolved substance or at temperatures over 400C. For the electrolytes (which dissociates) it does not apply anymore. The filtration is the separation of the components of a solution through a porous environment. Particles with a diameter higher than the diameter of the pores of that environment are retained. The ultrafiltration is a phenomenon analogue to filtration, having the pores with a very small diameter, which retain the macromolecules.

1. Vincze J (1967) About the transport phenomenon. Compte Rendu Acad Scien Paris, pp. 167-171.
2. Vincze J, Vincze Tiszay G (2023) The Human Mind. Philosophy Study 13(2): 60-67.