Model of HIV Infection Dynamics with Varying Source Parameters for the Rate of T-Cell Supply Through Using Contionus Galerkin-Petrov Time Discretization Scheme Volume 50- Issue 1

Adil Khurshaid¹*, Attaullah² and Salah Boulaaras³

• ¹Department of Mathematics, University of Swabi, Swabi, KP, Pakistan
• ²Department of Mathematics and Statistics, Bacha Khan University Charsadda, Pakistan
• ³Department of Mathematics, College of Sciences and Arts, ArRass, Qassim University, Saudi Arabia

Received: April 07, 2023;   Published: May 01, 2023

*Corresponding author: Adil Khurshaid, Department of Mathematics, University of Swabi, Swabi, KP, Pakistan

DOI: 10.26717/BJSTR.2023.50.007901

Abstract PDF

In this manuscript, a new approach termed as ”Continous Galerkin-Petrov” is imple- mented to create a mathematical model after the HIV infection that represents the be- havior of uninfected CD4+ T-cells, infected CD4+ T-cells, and free HIV pathogens. Over- all dynamics of healthy, infected CD4+ T-cells and free HIV pathogens are governed by the stream function for CD4+ T-cells replenishment from the thymocytes. We further looked at the impact of several adjustable parameterization on the stream of new CD4+ T-cells in extensive detail. Secondly, the framework is determined using the Runge Kut- ta technique of fourth order (RK-4 method). Finally, the suggested scheme’s reliability and validity are confirmed by analyzing the graphical and numerical results to the re- sults of RK4-method. The numerical and statistical results were compared to the RK4 approach, which indicated that the cGP(2) − method works quite well. In contrast to pre- vious conventional schemes, the consistency and efficiency of the suggested system are mentioned in this research.

Keywords: Azidothymidine; Didanosine; Dideoxycytidine; Anti-Retroviral Thera- py; Cluster of Differentiation 4; Cluster of Differentiation 8; Highly Active Anti-Retroviral Therapy; Continuous Galerkin- Petrov; Finite Element Method; Runge-Kutta Method of Order Four

The human immunodeficiency virus (HIV) targets the immune system. The immune system is the human body’s natural defence mechanism against illnesses. This system has number of biological structures in an organism for defence processes against disease. The main part of the human body defence system in blood cells is known as T-helper cells which destroyed by these viruses. Inside these cells, the virus makes copies by itself. The immune system of a person be totally destroyed due to untreated HIV virus. The HIV virus gradually breaks down person’s immune system by making more copies of itself, as it spiflicate more CD4+ T-cells. This means that without treatment someone that got HIV, find more troubles to fight off diseases and infections. If HIV patient is not given medical care, it may take 7-10 years [1] for the immune system to be so bad- ly spoiled that it can no more support itself in any respect. Breast milk, blood, semen, vaginal and anal fluids are the sources of presence of HIV. The transmission of HIV is not possible by urine, sweat or saliva. The set of symptoms caused by the HIV virus is called acquired immune deficiency syndrome (AIDS). When some people develop spe- cific symptoms and sicknesses, due to weakness of their immune system for fighting against infection are declare to have AIDS. This is the final phase of HIV and will lead to death without treatment. Unfortunately, there is no proper cure for HIV in present. The people effected with HIV can live healthy and long lives by taking treatment aright.

The human body’s innate immunity is a collaboration of several cells and tissues unitedly for supporting of the human body against attacks by extraneous invaders. There are two types of white blood cells that help the regulation of the immune function. One is devel- oped in bone marrow and produce antibodies called B-cells. The other is developed in a small organ in human body known as thymus gland called T-cells, which have respon- sibilities for the variety of some immune reaction. HIV is propagate from chimpanzees to human in early 1900’s. In the midwest, earliest case of AIDS appears in 1968’s. In 1987’s, the first citizen of Pakistan diagnosed with AIDS in Lahor. In Sub-Saharan Africa about twelve million children were effected with AIDS up to end of 2003’s. Numerous analogues for the body’s immune system have already been developed in recent years, and substantial investigation has been undertaken in the domain of HIV infection of CD4+ T-cells to comprehend HIV dynamical behavior, transmission, disease concatena- tion, as well as the immune system’s relationship with HIV. The destruction of CD4+ T-cells, which are required for the control of the human immune system, is one of the greatest havocs caused by HIV. As a result, the decrease in the number of these cells is employed as a main indication to track HIV epidemic concatenation and AIDS stages. Such cells generate at a steady pace from bone marrow and thymus precursors. Un- fortunately, there is currently no treatment for this contagious condition.

Now a days, the mathematical modeling have been used for understanding the transmitting of in- fectious diseases. The practise and theory of disease prevention and management are increasingly influenced by mathematical models for the transmission of infectious illnesses [1-8]. For uninfected T-cells and free virions, Ogunlaran, et al. [9] used a mathematical model with two control variables: the logistic growth function and the incidence term sequentially. The investigators looked at how effective medication interventions are at stopping new cells from becoming infected and prevent- ing the production of new free virus. They demonstrated the efficacy of the framework by reducing the accumulation of infected cells and free virus particles even while ex- panding the accumulation of healthy T-cells inside the internal organs with a minimal intake of combined drug therapies in order to alert the negative consequences associat-ed with excessive use of drug treatment. The powerful antiviral drugs are the hope of healthy life for the person effected by HIV virus. Coffin, et al. [10] examined long-term modification in virus load in an effected person dosed by the compounding of potent an- tiviral drugs lamivudine and zidovudine. Nowak, et al. [11] studied the function of body defence system for restricting virus and vary the drug immunity of virus load. Culshaw [12] incorporate a time delay into their mathematical model for reporting the time interval among viral infection of CD4+ T-cells and viruses fragment production from the patient’s psyche on a molecular level.

For finding of suitable conditions about the criterions in the framework for the innate and adaptive immunity steady states’ durability the Song [2] used the simple model with saturation response. Perelson [13] examined how dynamical modelling and parameter estimation methodologies have revealed significant aspects of HIV pathophysiology. The number of CD4+ T-cells in a typical person is estimated to be approximately 1000mm−3 [13]. The name of T-helper cells given to the CD4+ T-cells is because the major function of these T-cells is to transmit information towards other monocytes in order to regulate the body’s defensive mech- anism. As HIV infection progresses, the number of these cells decline. The CD4+ T- cells counts is 800 to 1200 mm−3 of those people which shows HIV negative [4]. When CD4+ T-cells calculate 200mm−3 or more below in a patient infected by HIV, then that person is sort to having AIDS [13]. Kumar, et al. [14] examined a dynamical mathematical model of HIV for understanding the infection of T-helper cells in human body. Boer, et al. [15] discussed a model which consist four components for the interacting of CD4+ T-cells and HIV virus. They developed estimations for changing at early time in which HIV virus particles binds to T-cells rapidly. Kirschner, et al. [16] introduced chemother- apy technique for an early treatment by using dynamic treatment. Bonhoeffer, et al. [11] discussed the incipient understanding of the dynamics of virus population. They al- so discussed the function of the body defence system in limiting virus abundance and changing of viral drug immunity.

Nowak, et al. [17] uses a simple mathematical tech- nique to explore the connection amongst antimicrobial immune responses, viral variety, and infectious strain. The potential of transmission of any disease in the human body is measured by a number known as the basic reproduction rate represented by R0. This reproduction number actually make a ratio of infection of healthy cells due to infected one. The mathematical models gives us very significant details about the HIV virus re- search. The linearity of the reproduction rate in all mathematical models demonstrates the efficiency of the participation between T-helper cells and HIV pathogens. Zhou, et al. [1] discussed the CD4+ T-cells infected by HIV virus by using crowley-martin function response. They discussed some properties of basic reproduction number. Zhou, et al. [7] discussed the differential equation model including cure rates. By using the char- acteristics of fundamental reproduction number R0, they showed that if R0 < 1 is used, the HIV virus infection is cleared and the sickness is eradicated, the infection of HIV virus remain in human body if R0 > 1. They found that the usual disease steady state is globally asymptotically stable if R0 >1.

There are a number of complex problems arising in the real world. These problems can be modeled in the language of mathematics. These problems can be defined by nonlinear ordinary differential equations (ODE’s). The importance of model increases as it gives best results having many variables. The variation of infection rate by HIV shows that the body defence system of the patient is the main target of HIV. The patient with strong immune system can survive more effectively against HIV. In other way, the patient with weak immune system can not survive against HIV for long period. This section discusses Zhou’s, et al. [7] suggested model, which comprises of non-linear differential equations. In the model, the total population is divided into three compartments. These are uninfected T-cells, infected T-cells and HIV virus particals. Let T(t), V(t) and I(t) be the population of healthy T-cells, free viruses and infected T-cells at time t respectively. The non-linear system of equations of the proposed model [7] are :

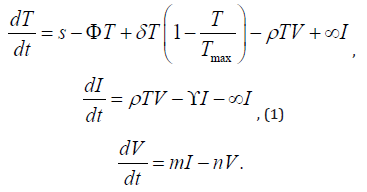
The continuous source term for the delivery of fresh T-cells is represented by the parameter ’s’. It is an indicator of how quickly the thymus as well as bone marrow gen- erates healthy T-cells [8]. The ϕ stands for the concentration of functional T-cells that die after being created by the body system. The letter ρTV represents the rate of dormant HIV infection in functional CD4+ T-cells. The infectious reaction rate is denoted by ρ. The δ stands for the maximum rate of intended cell proliferation, Tmax stands for the T concentration of people upon which cell escalation stops, γ stands for the death rate of infectious damage cells, m stands for the rate of infection cell reproduction, n stands for the rate of viral clearance, and α stands for the rate of curative treatment. (Table 1) lists the general system characteristics and indicators that were used in the creation of the framework. About the availability of fresh functional T-cells, Zhou, et al. [7] evaluated the HIV prototype with a constant variable stream function. HIV has the potential to contami- nate T-cells as soon as they enter the human body, which causes a decline in the number of young, functional T-cells [15]. For the purpose of providing new unaffected T-cells from the thymus, Boer, et al. [15] adopted an HIV model with changing source terms. Kirschner [3] and Webb, et al. [18] assume about the source phrase 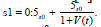s +V t The source term employed by Perelson, et al. [15] is 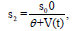where θ is constant. If V = 0, s₂ will stay the same and would be cut in half if the viral load V(t) increased to the point θ . Perelson, et al. [4] anticipated 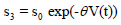as the source of the word. The HIV model with source termsimilar to that employed in the Perelson, et al. [15] model with θ =1 is also taken into consideration by (Kirschner, et al. [16]), Hermandes [19], Butler, et al. [5]. The primary goals of the current study are to investigate Zhou’s, et al. [7] model using all of the parameterization for the production of new cells indicated above. The dynamical behaviors of uninfected T-cells, free HIV virus particles, and infected T-cells will be explored in relation to the impact of fluctuation in the value of various clinical parameters. Arrangements can be obtained by employing the consistent Galerkin-Petrov technique. Runge Kutta technique of order four (RK-4) will also be used to obtain numrical solutions of the proposed model. A computer programme created in MATLAB will be used to calculate all the findings. To better comprehend the implications of multiple source terms, graphical outcomes will be shown.

The Steady States [6,8]

In the real problem system in mathematical model, if variables which are using in the model do not show any variation with respect to time duration, then this system is in steady state. In a mathematical model, the untreated and diseased steady states are the two basic types of steady conditions.

Uninfected Steady State

If the human body shows no virus present in it and not any infected CD4+ T-cells present in it, this state is known as uninfected steady state. The virus presence in uninfected steady state in any human is zero. In the studying model for uninfected steady state, T = T0, I = 0 and V = 0. We calculate the uninfected steady state T0 for the studying model given above as:

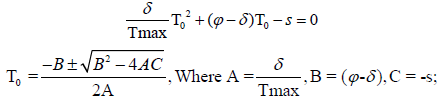
By using quadratic formula we calculate the uninfected steady state T₀ i.e.,

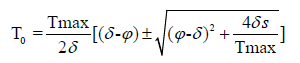
Infected Steady State

If the human body shows virus and infected CD4+ T-cells present in it, this state is known as infected steady state [20]. By putting T=¯T, I=¯I and V=¯V in the under discussion model we find out the values of

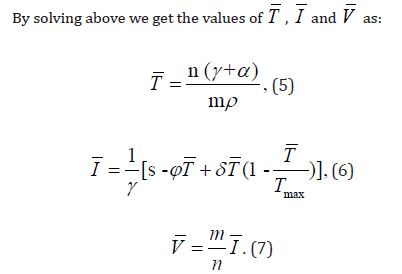
For positive infected stable state we examine local stability by utilizing Routh- Hurwitz standards [12]. First we find the jacobin matrix. For this the jacobin matrix J is

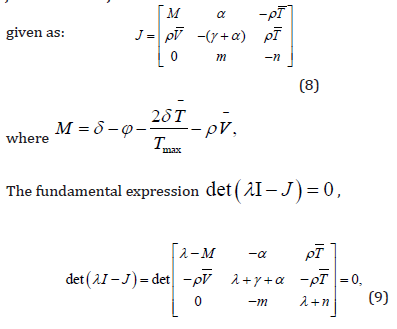
the characteristic equation of linearized system is :

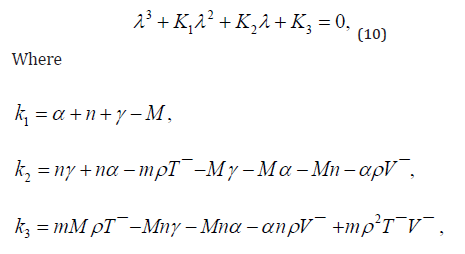
The equation 10 under discussion have negative real parts for all of its eigne values iff [12], K₁ > 0 , K₂ > 0 , K₁K₂ − K₃ > 0.

For positive infected steady state E₀ (T₀,0,0) ,we examine local stability by using Routh- Hurwitz standards [12]. First we find the jacobin matrix. For this the jacobin matrix J is given as:

For linearized system of equations, the characteristics equation is:

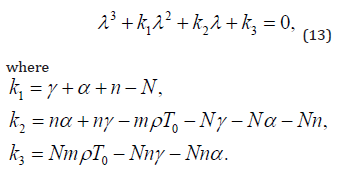
The equation 13 under discussion have negative real parts for all of its eigne values iff [12],

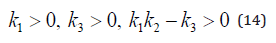
The reproduction ratio is quite smaller in model [7] with cure rate. Due to this, it is easy to control the disease and also decrease the infection speed of new HIV virus. The reproduction ratio is quite larger in model [7] without cure rate. Due to this, it is not easy to control the disease and also increase the infection speed of HIV virus. We demonstrate that the fundamental reproduction number R₀ can generates a comprehensive prescription of the model [7] global interactions. According to the framework’s fundamental reproduction number 0 R ,the equilibrium of the proposed infectious model is asymptotically stable if R0 <1, and On the other side, the pandemic model’s equilibrium has a special endemic equilibrium if 0 R >1,and is likewise globally asymptotically stable. The model under discussion [7] hav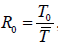e where , without cure rate and be with cure rate, this modified as 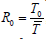where 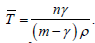The comparison of the model with and without cure rate demonstrates that when compared to models lacking cure rates, the virus’s rate of infection is extremely sluggish. Therefore, the prototype with the highest treatment regimen will be preferred.
Theorem 1. Suppose that

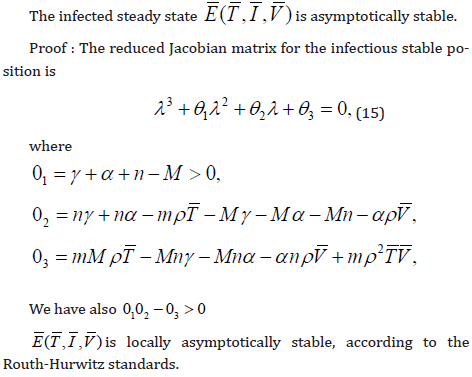
Theorem 2. System 1 is a competitive system. Proof: For the system of equation [7], taking the matrix L as:

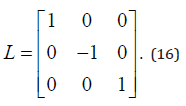
To defining partial order by the orthant, this system is competitive in D.

We obtained with the fact of simple calculation,

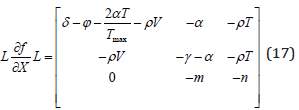
Due to convexity of D, this system is competitive in D. In view of this Poincare-Bendixson property is satisfied by the system.

The HIV model’s system of ordinary differential equations could be characterised as:
Take into account a time period  = [0,T ]with an ultimate time T that is positive.We find

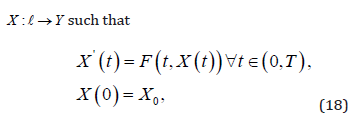
The assumption is that the function F : L ×Y →Y is sufficiently smooth which can be nonlinear.
To express the temporal discretization of the issue [18], we now initiate the following syllabaries. We select a subinterval K ⊂ L to describe the steadiness of the function t → X (t ).We take into consideration a set of m times continuously differentiable Y -valued functions

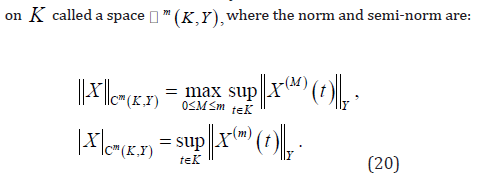
Now, we obtain the collection of subintervals by dividing time interval 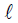into N subintervals 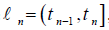, which is known as the time-mesh R . Ω We use the time discretization parameter represented by the maximal time step size Ω , where

or in discontinuous time-discrete space

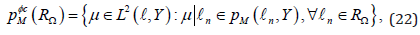
where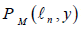 is a space of polynomials in time t with vector values of order M, i.e.,

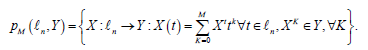
For discrete function X : →Y, that are discontinuous at the end points of time intervals, we define the left-sided and right-sided values X n− n and X n+ as well as the jump [X _Ω]_n respectively:

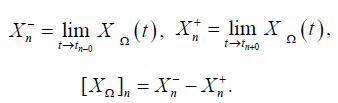
Moreover, we define the function values 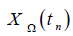with n ≥1 on the interval 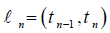will be 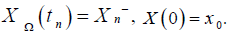. Here, we employ the spac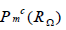e as a time-discrete solution space and the space 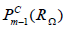as a discrete test space. The discrete solution X_Ω has 􀀀 .M many undetermined degrees of freedom due to the beginning circumstances in Equation (18), and the test space size is also 􀀀 .M .We multiply Equation (18) by the test function

with 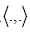denoting the usual inner product in 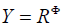.The precise continuous Galerkin- Petrov technique of order M, also known as the exact cGP(K)⁻ method, will be used to refer to this discretization. The test space 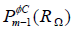differs from the ansatz space 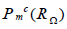,therefore earning the moniker Galerkin-Petrov. Exact refers to precisely evaluating the integral on the right side of issue (23). Since 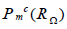space is discontinuous, the problem (23) can be solved by a time marching process where successively local problems on the time intervals are solved. For this purpose, we select a test function 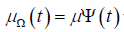with an arbitrary time independentμ ∈Y and 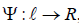, a scalar function which becomes zero on 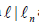and a polynomial of orderless than or equal to M −1on . l_n Then, from problem(23), we get l_n− problem of exact cGP(K)⁻ method, i.e., Find

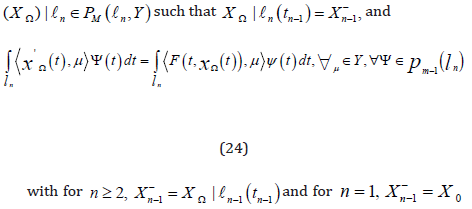
We numerically estimate the integrals on the right side of Equation (24) for non-linear functions. If the integrated function is a polynomial with degree less than or equal to 2M −1,the (M +1)⁻ point Gauss Lobatto formula is accurate. In order to obtain the precise value, we apply this formula to the left side of Equation (24). Now, we take reference interval 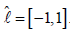.Denote the associated weights and nodes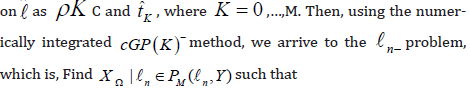

At this point, we use an affine reference transformation to define

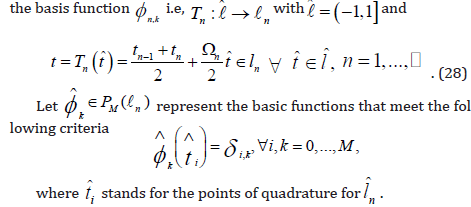
This results in the following formula for each test basis function ψ and∀μ ∈Y ,

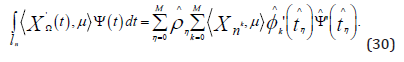
cGP(1) −Method

The Trapezoidal rule is produced by applying the two-point Gauss-Lobatto formula with the weights 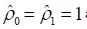and the quadrature points 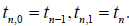Then, we acquire 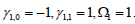. The solution to this issue yields the block-equation shown below, where coefficient

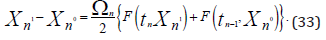
cGP(2)-Method

Now,we utilise the Three-point Gauss-Lobatto algorithm to get the Simpson’s rule using the weigh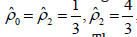ts and the quadrature points 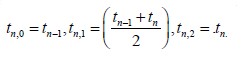The coefficients were then computed as,

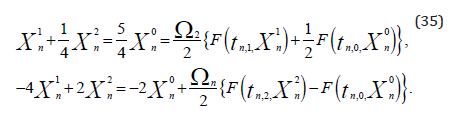
In this research paper, we obtained the results of the model [7] by using the cGP(2)⁻ method and demonstrate the results graphically and numerically. The detailed values of different parameters used in the model are discussed in the (Table 1). We graphically depict the variations in the population of healthy T-cells, infectious T-cells, and free HIV pathogens with constant and varied variable source terms. The graphic findings of T(t), I(t) and V(t) demonstrate decaying oscillatory behaviour with somewhat different population dynamics employing variable and invariant source terms. (Figure 1) shows the effects of variable source term on healthy CD4+ T-cells. It is obvious that populace flow of healthy CD4+ T-cells changes with the change of invariant source terms. From the (Figure 1), It is clear that populace flow of T-cells of source term s3 appears significantly different from source terms s0, s1 and s2 throughout the time period. Similar behaviour is seen for the population dynamics of infected T-cells and free HIV virus particles in (Figures 2 & 3) respectively, whenever these source terms are impacted.

Table 1: An overview of the model’s parameters, variables, and their values.

Figure 1

Figure 2

Figure 3

Figure 4

Figure 5

Figure 6

For the verification of results, we also find solution by using RK-4 method graphically and numerically [23]. It is seen that results obtained from both methods, cGP(2)⁻ method and RK-4 method, are in great interest with each other (Tables 2 & 3). From comparison it is observe that, for the model compared to existing approaches, including HPM [24], LADM [25,26], MVIM [21], VIM [22], the suggested method yields findings which are highly consistent. We illustrate the results of both methods graphically through (Figures 4-6). The graphical results are over lapping and this leads to the accuracy of cGP(2)⁻ method [27]. Results depicted in (Figures 4-6) shows that cGP(2) method and classical RK-4 method are in great agreement [28-30]. These findings suggest that the cGP(2)⁻ method should properly forecast how these variables would behave in the region under consideration [31,32].

Table 2: Results of cGP(2) for T(t), I(t) and V(t).

Table 3: Results of RK4 method for T(t), I(t) and V(t).

In this manuscript, the cGP(2)⁻ technique is being used to give the numerical results of a comprehensive framework for HIV infection of healthy T-cells. Researchers wanted to know how the availability of fresh, competent T-cells from the thymus would affect the HIV infection prototype, both in terms of constant and varied changeable source terms [33,34]. The analysis showed that the interaction of healthy T-cells, infected T-cells, and free HIV virus particles communicate in a dulled fluctuating way for all types of source terms during the time frame, although their population rates only undergo minor variations. Regarding source term s3, there is a dramatic shift in T(t), I(t) and V(t) absorption over time duration, but for other source terms, the dynamical behaviour is almost the same at first and then modifications only become visible subsequently. Throughout the phase diagram, all of the source terms initially have complexities that are comparable to one another, but their population dynamics diverge from one another over time duration. On the other side, we used the RK4-method to solve the problem and have quantified comparisons of the T(t), I(t) and V(t) solutions generated by utilising cGP(2)⁻ method, RK4-method, and other traditional approaches. Last but not least, we represented the numerical curves produced by the cGP(2)⁻ method and RK4-method. We find it noteworthy that, when compared to other approaches utilised for the HIV infection framework, the effectiveness of the cGP(2)⁻ method and the RK4-method is almost the same.

1. X Zhou, J Cui (2011) Global stability of viral dynamics with crowley-martin functional response. Bul Korean Math Soc 48(3): 555-574.
2. X Song, AU Neumann (2007) Global stability and periodic solution of the viral dynamics. J Math Anal 329(1): 281-297.
3. D Kirschner (1996) Using mathematics to understand HIV immune dynamics. 43 (11): 191-202.
4. SA Perelson (1989) Mathematical and Statistical Approaches to AIDS Epidemiol- ogy. Springer-Verlag 48.
5. S Butler, D Kirschner, S Lenhart (1997) Optimal control of chemotherapy affect- ing the infectivity of HIV. Ann Arbor 1001: 0620-48109.
6. F Schieweck (2010) A stable discontinuous Galerkin Petrov time discretization of higher order. Journal of Numerical Mathematics 18: 25-57.
7. X Zhou, X Song, X Shi (2008) A differential equation model of HIV infection of CD4⁺T-cells with cure rate. J Math Anal Appl 342(2): 1342-1355.
8. X Wang, X Song (2007) Global stability and periodic solution of a model for HIV infection of CD4+ T-cells. Journal of Applied Mathematics and Computation 189: 1331-1340.
9. OM Ogunlaran, SCO Noutchie, (2016) Mathematical model for an effec- tive management of HIV infection. Hindawi Publishing Corporation Bio-Med Research International Article ID: 4217548.  
10. S Bonhoeffer, JM Coffin, MA Nowak (1997) Human immunodeficiency virus drug therapy and virus load. Journal of virology 77(4): 3275-3278.
11. S Bonhoeffer, RM May, GM Shaw, MA Nowak (1997) Virus dynamics and drug therapy. Proc Natl Acad Sci USA Medical Sciences94(13): 6971-6976.
12. RV Culshaw, S Ruan (2000) A dealy-differential equation model of HIV infection of CD4⁺ T-cells. Mathematical Biosciences 165(1): 27-39.
13. AS Perelson, PW Nelson (1999) Mathematical analysis of HIV-1 dynamics in vi-vo. Society for industrial and applied mathematics41(1): 3-44.
14. VK Srivastava, MK Awasthi, S Kumar (2014) Numerical approximation for HIV infection of CD4⁺ T-cells mathematical model, Ain Shams Engineering Journal 5(2): 625-629.
15. AS Perelson, DE Kirschner, RD Boer (1993) Dynamics of HIV infection of CD4⁺ T-cells. Mathematical Biosciences 114(1): 81-125.
16. D Kirschner, S Lenhart, S Serbin (1997) Optimal control of the chemotherapy of HIV. J Math Biol 35(7): 775-792.
17. MA Nowak, CRM Bangham (1996) Population dynamics of immune responses to persistent viruses. Science 272(5258): 74-79.
18. D Kirschner, GF Webb (1996) A model for HIV treatment strategy in the chemotherapy of AIDS. Bulletin of Mathematical Biology 58(2): 367-390.
19. JXV Hermandez, JA Garcia, D Kirschner. Remarks on modeling host-pathogen systems.
20. RJD Boer, AS Perelson (1998) Target cell limited and immune control models of HIV infection: A comparison. Journal of theoretical Biology 190(3): 201-214.      
21. AK Aziz, P Monk (1989) Continuous finite elements in space and time for the heat equation. Math Comp 52(186): 255-274.
22. M Merdan, A Gokdogan, A Yildirim (2011) On the numerical solution of the model for HIV infection of CD⁴⁺ T-cells. Comput Math Appl (62): 118-123.
23. E Barkanov (2001) Introduction to the finite element method. Institute of materials and structures faculty of civil engineering Riga technical uni Riga.
24. M Medan (2007) Homotopy perturbation method for solving a model for HIV infection of CD4⁺ T-cells. Istanbul Tipcart Universities Fen Balmier Derris Yell 39-52.
25. JJ Kutch, P Gurfil (2002) Optimal control of HIV infection with a continuously mutating viral population. Proc of Amer Control Conf 4033-4038.
26. M Y Ongun (2011) The laplace adomian decomposition method for solving a model for HIV infection of CD4⁺ T-cells. Mathematical and Computer Modeling 63: 597-603.
27. Thomas, M Morari, Book: Lecture notes in control and information sciences. Delays effects on stability A robust control approach.    
28. M Anthea, J Hopkins, CW Mclaughlin, S Johnson, MQ Warner, et al. (1993) Human biology and health. Englewood Cliffs New Jersey USA: Pren- tice Hall 19-47.
29. P William (2004) Life: The science of biology, 954. CD4⁺ T-cells. Math Biosciences 114: 81-125.
30. (2016) Iosr Journal of Dental and Medical Sciences. 3(15): 38-41.
31. M Falguni, J Hrishabh (2016) Finite Element Methode. An Overview, Journal of Dental and Medical Sciences p.38-41.
32. MF Verlag (2012) Layout and Printing: Agentur, Vopeliuspfad 6, 14169 Berlin Pictogram, Tobias Emskoetter.     
33. D Kirschner, D Mehr, AS Perelson (1996) The role of the thymus in HIV infection. Journal of Acquired Immune Deficiency Syndromes and Human Retrovirology.
34. JM Mccune (2001) Part-I: Dynamics of immune system against HIV, Journal of Nature 410: 974-979.