Oscillatory Behavior of Second Order Nonlinear Difference Equations with Mixed Neutral Terms Volume 47- Issue 4

Said R Grace*

• Department of Engineering Mathematics, Faculty of Engineering, Cairo University, Egypt

Received: November 28, 2022;   Published: December 09, 2022

*Corresponding author: Said R Grace, Department of Engineering Mathematics, Faculty of Engineering, Cairo University, Orman, Giza 12221, Egypt

DOI: 10.26717/BJSTR.2022.47.007522

Abstract PDF

ABSTRACT

This paper deals with the oscillation of second order nonlinear difference equations with mixed nonlinear neutral terms. The purpose of the present paper is the linearization of the considered equation in the sense that we would deduce oscillation of studied equation from that of the linear form and to provide new oscillation criteria via comparison with first order equations whose oscillatory behavior are known. The obtained results are new, improve and correlate many of the known oscillation criteria appeared in the literature. The results are illustrated by some examples.

Keywords: Second Order; Nonlinear; Neutral; Mixed Type; Oscillation AMS (MOS) Classification 34N05, 39A10

Introduction

This paper is concerned with oscillatory behavior of all solutions of the nonlinear second order difference equations with mixed neutral terms of the form

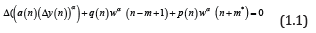
where

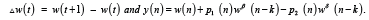
We shall assume that

α,β,γ,μ” and “ δ are the ratios of positive odd integers,α≥1

{p_1 (n)},{p_2 (n)}, {q (n)} and {p (n)} are sequences of positive real numbers.

k, m, m*are positive real numbers with h (n) = n– m + k + 1 and h* (n) = n + m* + k.

We let

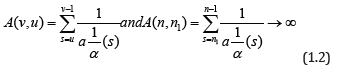
for

. By a solution of equation (1.1), we mean a real sequence {x(t)} defined for allt≥t_0-θ and satisfies equation (1.1) for all t≥t_0. A solution of equation (1.1) is called oscillatory if its terms are neither eventually positive nor eventually negative, otherwise it is called nonoscillatory. If all solutions of the equation are oscillatory then the equation itself called oscillatory. In recent years, there has been a great interest in establishing criteria for the oscillation and asymptotic behavior of solutions of various classes of second-order difference equations, see [1-15] and the references cited therein. However, to the best of our knowledge, there are no results for second-order difference equations with mixed neutral terms of type (1.1). More exactly, existing literature does not provide any criteria which ensure oscillation of all solutions of equations (1.1). The aim of the present paper is the linearization of equation (1.1) in the sense that we would deduce oscillation of studied equation from that of the linear form and to provide new oscillation criteria (taking the linear form of equation (1.1) into account) via comparison with first order equations whose oscillatory behavior are known. The obtained results are new, improve and correlate many of the known oscillation criteria appeared in the literature for equation (1.1).

Main Results

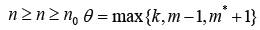
In this section we study some oscillation criteria for equation (1.1) when β<1” and “ δ>1. We start with the following fundamental result. See [10, Lemma 1], and for the proof of (I), see [15, Lemma 2.2].

Lemma 2.1. Let {q (n)} be a sequence of positive real numbers, m and m*are positive real number and f: R→ R is a continuous nondecreasing function, and x f(x) > 0 for x≠0,

The first order delay differential inequality

y(n) + q(n) f ( y(n −m+1)) ≤ 0 has an eventually positive solution, so does the delay equation

y(n) + q(t) f ( y(t −m+)) ≤ 0

The first order advanced differential inequality

y(t) − q(n) f ( y(n + m*)) ≥ 0 has an eventually positive solution, so does the delay equation y(n) − q(n) f ( y(n + m*)) = 0 Lemma 2.2. [13]. If X and Y are nonnegative, then

X^λ + (λ −1)Y^λ −λ XY^{λ −1} ≥ 0 forλ >1, (2.1)

X^λ − (1−λ )Y^λ −λ XY^{λ −1} ≤ 0 for0 < λ <1 (2.2)

where equality is held if and only if X = Y.

In what follows, we let

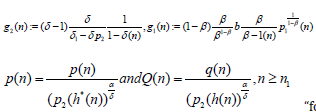
"for some n"≥n_0," where " {b (n)} is a sequence of positive real numbers

Now, we present the following oscillation result. Theorem 2.1. Let β<1” and “ δ>1, conditions (i) – (iv) and (1.3) hold. Assume that there exist positive sequences (b (t)} and positive real numbers k₁and k₂ such that k₁ < m-k₁ and k₂ < m* + k +1 such that

(2.3)

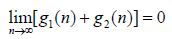
If the first order advanced equation

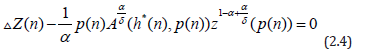
is oscillatory, where ρ(n) = n +m*+k-k_2>t, and assume that there exists a number θ∈(0,1) such that both the delay equations

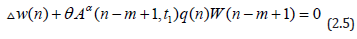
for some n₁≥n₀ and

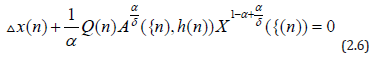
where, ξ(n)=n-m+k₁+1<t

Proof. Let {w (n)} be a nonoscillatory solution of equation (1.1), say w (n) > 0, w(n-k)>0 ,w(n-m+1)>0 , and w(n+ m*+1)>0 for n≥n₁ for some n₁≥n. It follows from equation (1.1) that

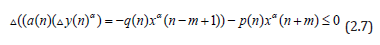
Hence

is nonincreasing and of one sign. That is, there exists a

such that

Now, we see that

Taking the difference of the above inequality, we get

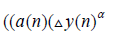
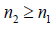
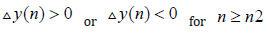
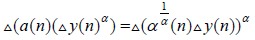
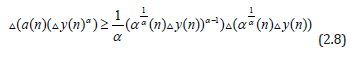
From equation (1.1) one can easily see that

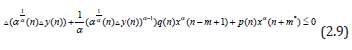
From (2.9) one can easily get

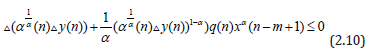
We shall distinguish the following four cases:

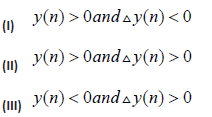
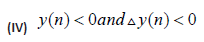
First, we consider Case (I): Since

By condition (1.2), we conclude that

a contradiction to the fact that y (n) is eventually positive. Next, we consider Case (II). Now, from the definition of y (n), we get

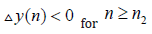
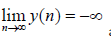
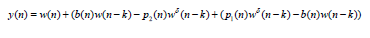
Or

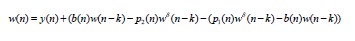
If we apply (2.1) with

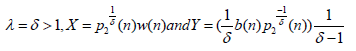
we have

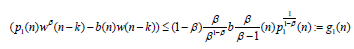
Thus, we see that

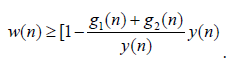
Since y (t) in nondecreasing, there exists a constant C > 0 such that y(n)≥C , and so, we have

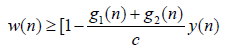
Now, there exists a constant c₁∈(0,1) such that

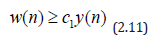
Using (2.11) in (2.10), we have

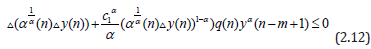
Clearly, we see that

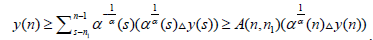
Using this inequality in (2.12), we find

(2.13) It is easy to see that the function

(2.13) is a nonincreasing and so, we get

(2.14) We let

and

so, we see that

Using this inequality in (2.14), we have

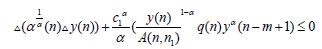
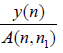
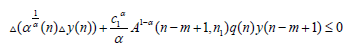
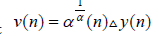
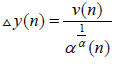
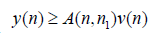
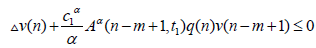
It follows from Lemma 2.1. (I) that the corresponding differential equation (2.5) also has a positive solution, a contradiction. Next, we consider the cases when y (n) < 0 fort≥t₂.

Let

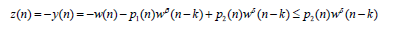
Or

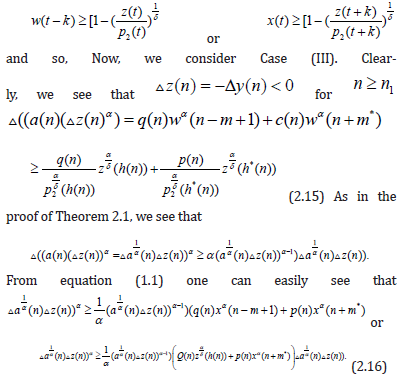
From (2.16) one can easily find that

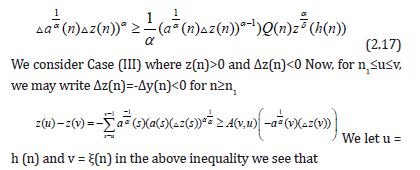
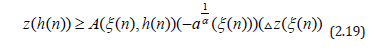
Using (2.19) in (2.17), we have

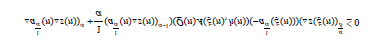
which finally takes the form

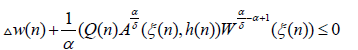
where W (n) =

. The rest of the proof is similar to that of Case (I) and hence is omitted. Next, we consider Case (IV), i.e., z(n)>0 and Δz(n)>0. Now,

Remark 2.1.

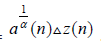
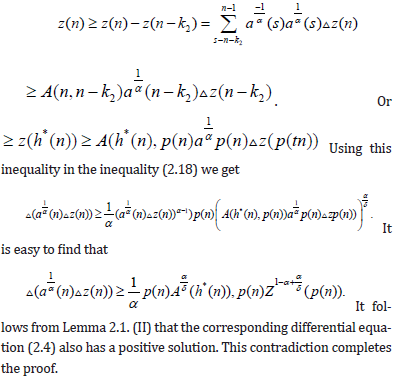
We note that the results of this paper can be extended easily to the more general equations of the for

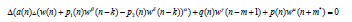
where the coefficients are the same as in equation (1,1) with γ and μ are the ratio of positive odd integers. The details are left to the reader. For the special case when α= δ, i.e. ,the equation &

(2.20) and when α=1,i.e.,the equation

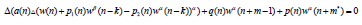
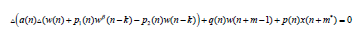
(2.21) we have the following interesting results Corollary 2.1. Let the hypotheses of Theorem 2.1 hold with equations (2.4) and (2.6) are replaced (respectively) by:

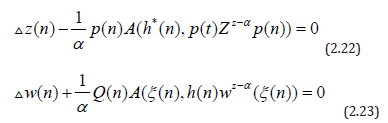
(2.23) Then equation (2.20) is oscillatory.

We also have the following result from corollary 2.1 for equation (2.21): Corollary 2.2. Let the hypotheses of Theorem 2.1 hold with equations (2.4) and (2.6) are replaced (respectively) by

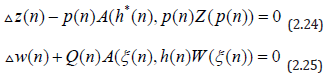
Then equation (2.21) is oscillatory.

The following corollary is to employ some integral conditions rather than the oscillatory behavior of first order equations involved. Corollary 2.3. Let the hypotheses of Theorem 2.1 hold. If

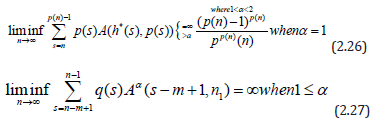
And

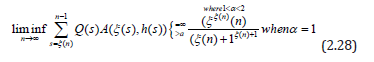
then equation (2.20) is oscillatory. The following example is illustrative: Example 2.1. Consider the mixed neutral second order differential equations

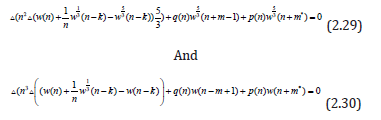
Here we have

are are positive sequences of real numbers ,a (n)= n³,A(n,n₁ )=

p_1 (n)=1/n→0 as n→∞ and p_2 (n)=1=b(n), α =5/3= δ and β=1/3, k, m,m^*are positive real numbers with h (n) = n – m + k + 1 and h* (n)=n+m*+k and positive real numbers k₁ and k₂ such that k₁ < m-k₁ and k₂ < m* + k +1 with ρ(n) = n +m*+k-k₂>n and ξ(n)=n-m+k₁+1<n. It is easy to see for appropriate function p and q and the numbers k₁ and k₂ that all conditions of Corollary 2.3 are satisfied and hence every solution x (t) of equation (2.29) (respectively (2.30)) is oscillatory.

Remarks

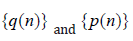
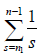
The paper is presented in a form which is essentially and of high degree of generality. It will be of interest to study these results for the higher order of the

Competing Interests

The author declare that they have no competing interests.

Data Availability Statement

Not Applicable.

References

1. Agarwal RP (2000) Difference Equations and Inequalities Theory, Methods, and Applications (2^nd)., Monographs and Textbooks in Pure and Applied Mathematics vol 228 Dekker, New York.
2. Agarwal RP, Bohner M, Grace SR, O’Regan D (2005) Discrete Oscillation Theory Hindawi Publishing Corporation New York.
3. Agarwal RP, Bohner M, Li T, Zhang C (2014) Oscillation of second-order differential equations with a sublinear neutral term. Carpath J Math 30(1): 1-6.
4. Agarwal RP, Bohner M, Li T, Zhang CA (2014) Philos-type theorem for third-order nonlinear retarded dynamic equations. Appl Math Comput 249: 527-531.
5. Agarwal RP, Grace SR, O’Regan D(2000) Oscillation Theory for Difference and Functional Differential Equations Kluwer Academic, Dordrecht.
6. Dharuman CP, Graef JR, Thandapani E, Vidhyaa KS (2017) Oscillation of second order difference equation with a sub-linear neutral term. J Math Appl 40: 59-67.
7. El-Morshedy HA, Grace SR(2005) Comparison theorems for second order nonlinear difference equations. J Math Anal Appl 306(1): 106-121.
8. Grace SR (2019) Oscillatory behavior of third-order nonlinear difference equations with a nonlinear-nonpositive neutral term. Mediterr J Math 16(5).
9. Grace SR, Bohner M, Agarwa RP (2009) On the oscillation of second-order half-linear dynamic equations. J Differ Equ Appl 15(5): 451-460.
10. Grace SR, Bohner M, Liu A (2010) On Kneser solutions of third-order delay dynamic equations. Carpath J Math 26(2): 184-192.
11. Grace SR, El-Morshedy HA (2000) Oscillation criteria of comparison type for second order difference equations. J Appl Anal 6(1): 87-103.
12. Grace SR, Graef JR (2018) Oscillatory behavior of second order nonlinear differential equations with a sublinear neutral term. Math Model Anal 23(2): 217-226.
13. Hardy GH, Littlewood JE, Pólya G (1988) Inequalities Cambridge Mathematical Library Cambridge University Press, Cambridge Reprint of the 1952 edition.
14. Shoukaku Y (2017) On the oscillation of solutions of first-order difference equations with delay. Commun Math Anal 20(2): 62-67.
15. Li Q, Wang C, Li F, Liang H, Zhang Z (2006) Oscillation of sublinear difference equations with positive neutral term. J Appl Math Comput 20(1-2): 305-314.