Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
S Pashiardis1*, SA Kalogirou1** and A Pelengaris2
Received: November 22, 2022; Published: December 06, 2022
*Corresponding author: S Pashiardis, Department of Mechanical Engineering and Materials Science and Engineering, Cyprus University of Technology, P. O. Box 50329, 3603, Limassol, Cyprus
DOI: 10.26717/BJSTR.2022.47.007502
In this study, hourly measurements of global solar irradiances, photosynthetically active radiation (PAR) and daily sunshine duration are assessed through an extensive quality control procedure and statistical analysis on the measured and derived solar and PAR indices for a semi-mountainous location using data from the last five years (2016-2020). From this analysis the seasonal characteristics of PAR and its derived indices are examined. This information is useful for agronomists and agrometeorologists who are interested in the efficiency of crop productivity and therefore they are interested on the levels of PAR radiation. Monthly mean hourly values of the radiation components are estimated and shown through isoline diagrams. Monthly mean daily PAR generally increased from 13.7 mol/m2/d in December to 49.8 mol/m2/d in July with an annual mean value being 31.4 mol/m2/d. Simultaneously, similar analysis is carried out over various PAR indices estimated on both hourly and daily basis. Monthly mean daily fFECd (ratio of daily Photosynthetic Photon Flux Density (PPFD) to daily global irradiation) increased from 1.77 mol/MJ in April to 1.83 mol/MJ in January with an annual mean value being 1.80 mol/MJ. Clearness index (KT) was used for characterizing sky conditions, and it was discovered that clear skies represent 40.4 % of the days in a year, while cloudy conditions are recorded in 12.2 %. Generally, fFECd is decreased from 1.91 mol/MJ under cloudy conditions to 1.77 mol/MJ under clear sky conditions, which is due to the strong absorption and scattering effects of clouds on longer wavelengths. The annual average of daily clearness index (KT) is 0.565 with a standard deviation of 0.161. One linear and one multilinear model as well as three power law models were tested and validated under all sky conditions. The best performance was obtained from the linear relationship between PPFD and global irradiance, while the second one was the multiple regression model based on global irradiance and clearness index. The rest four models use power law equations based mainly on clearness index, optical air mass and cosine of solar zenith angle. All the models showed high coefficients of determination (R2) which are closed to 1.
Abbreviations: AFclear: Ratio of PARE clear to the extraterrestrial one (PARE0); AST: Apparent Solar Time (hour): Bn: Hourly normal beam irradiance (W/m2); c: Correction for summer time (c=1 for summer and c=0 for winter); CDF: Cumulative density function; CV: Coefficient of variation (%); dn: Day number of the year (1..365); ea: Screen level actual water vapour pressure (kPa or hPa); es: Saturated screen level water vapour pressure (kPa or hPa); Ei: Estimated irradiance (W/m2); Et: Equation of time (min); ERL: ‘Extremely rare’ (ERL) limits (W/m2); fFEC: Hourly fraction of PPFD to global radiation (μmol/J); fFECd: Daily fraction of PPFDd to global irradiation (Gd) (mol/MJ); fPAR:Hourly fraction of PARE to global radiation; fPARd: Daily fraction of PAREd to global radiation (Gd); G: Hourly global solar irradiance (W/m2); Gd: Daily global solar irradiation (MJ/m2); G0: Hourly Extraterrestrial horizontal irradiance (W/m2); : Daily extraterrestrial irradiation (ETR) (MJ/m2); Gc: Clear-sky global solar irradiance (W/m2); Gcd : Daily global irradiation for clear-sky conditions (MJ/m2); Gsc:: Solar constant (1367 Wm2); Gmax: Highest daily global solar irradiance (W/m2); kPAR: Hourly PAR Clearness index (PARE/PARE0; KPAR: Daily PAR Clearness index (PAREd/PARE0d); kt: Hourly clearness index (G/G0); KT: Daily clearness index (Gd/G0d); LF: Conversion factor for PAR irradiance (4.57 μmol s-1 W-1) (McCree, 1972); m: Optical air mass; Mi: Measured irradiance (W/m2); MBE: Mean Bias Error; MMH: Mean Monthly Hourly; n: Number of observations; N: Number of days; PARE: Hourly Photosynthetic Active Irradiance (W/m2); PAREd: Daily Photosynthetic Active Irradiation (MJ/m2); PARESC: PAR Solar constant (534.6 W/m2); PARE0: Hourly Photosynthetic Active Irradiance at the top of the atmosphere (W/m2); PARE0d: Daily Photosynthetic Active Irradiation at the top of the atmosphere (MJ/m2); PPFD: Hourly Photosynthetic Photon Flux Density (μmol s-1 m-2); PPFDclear: Hourly Photosynthetic Photon Flux Density under clear sky (μmol s-1 m-2); PPFDx: Maximum hourly Photosynthetic Photon Flux Density (μmol s-1 m-2); PPFD0: Hourly extra-terrestrial Photosynthetic Photon Flux Density (μmol s-1 m-2); PPFD0d: Daily extrterrestrial Photosynthetic Photon Flux Density (mol m-2 d-1); PPL: ‘Physically possible’ limits (W/m2); P/P0: Pressure correction for station height; Q1: First Quartile; Q3: Third Quartile; R2: Coefficient of determination; RE: Relative percentage error (%); RH: Relative humidity (%); RMSE: Root Mean Square Error; S: Standard deviation of residuals; Sd: Daily sunshine duration (hours); S0d: Astronomical day length (hours); StDev: Standard deviation (Std); SW: Shortwave radiation Local time (hour); Ta(°C): Air temperature at screen level (0C), Ta(K)=273.16+ Ta(°C); Td: Dew point temperature (0C); VPD: Vapor pressure deficit (kPa or hPa); z: Station’s elevation (m)
Greek:
αs Solar altitude angle (degrees)
δ Solar declination angle (degrees)
δr(m) Rayleigh optical depth at air mass m
ε Correction factor to mean solar distance
θz Solar zenith angle (SZA) (degrees)
λ Longitude of the station in degrees (East positive)
λSTReference longitude of the time zone in degrees (for Cyprus= 300)
μ Cosine of solar zenith angle (cos(θz))
σ Relative sunshine duration (Sd/S0d)
φ Latitude of the station in degrees
ω Hour angle (degrees)
ωs Sunset hour angle (degrees)
Keywords: Mindfulness; Awareness; Posture; Female; Goals
Photosynthetically Active Radiation (PAR) is defined as the electromagnetic radiation in the waveband between 400 and 700 nm, which can be used as a source of energy for photosynthesis by green plants [1,2]. PAR is a key parameter in many physical, chemical and biological processes, such as plant physiology, crop growth, biomass production [3,4]. It is a key variable in a wide range of ecophysiological models, both at leaf photosynthesis level (Penning de Vries, et al. [5,6]) and crop production level [7]. Moreover, accurate PAR measurements are important for the determination of deforestation and climate-change impacts on agriculture (Pei, et al. [8,9]). Meanwhile, reconstruction of PAR during the last decades has gained much scientific interest in China with respect to the global climate-change (Zhu, et al. [10-12]). PAR is expressed either in terms of Photosynthetic Photon Flux Density (PPFD) in units of μmol /s/m2, since photosynthesis is a quantum process, or in terms of energy (PARE, Photosynthetically Active Radiation) in units of W/m2 [13], which is more suitable for energy balance studies. Usually, PPFD is recorded, and converted into energy units according to the McCree conversion factor of 4.57 μmol/J ±3% depending on climatic factors [14]. For the diffuse component, under blue sky an average value of 4.28 μmol/J was reported (Jacovides, et al. [15]). In the presence of clouds, the factor increases from 4.24 μmol/J to the value of 4.57 μmol/J under overcast conditions [16].
PAR is measured only in a limited number of stations around the world. This parameter is often indirectly calculated from global horizontal radiation. Therefore, it can be also expressed as (a) a fractional energy of PAR to global radiation (fPAR=PARE/G), (b) as a fraction of photon flux to the global radiation (fFEC=PPFD/G) in μmol/J or in mol/MJ for daily values and (c) as a clearness index (KPAR=PARE/PARE0) i.e., the ratio of PAR to the extraterrestrial PAR irradiance. The ratio fPAR falls between 0.40 and 0.50 (Papaioannou, et al. [17,18]). Values above 0.50 occur under very low sun or thick cloud cover (Alados, et al. [19]). suggested that a constant ratio of 0.50 can be used for practical applications regardless of atmospheric aerosols and water vapor concentrations. Regarding the conversion efficiency (fFEC), it was found that this ratio varies between 1.7 and 2.9 μmol/J (Alados et al. [19-24]). This ratio increases with water vapor content and cloud amount but decreases with aerosol loading and the solar zenith angle [24-27]. This fact is attributable to cloud-related absorption and diffusion of solar radiation across different regions of the spectrum. The presence of water vapor increases the absorption effects within the infrared region of the spectrum, decreasing broadband solar irradiance levels to a greater extent than PAR. A secondary effect of water content is the enhancement of aerosol-related diffusion, which affects PAR more than broadband solar irradiance (Alados, et al. [19]). The fraction of PAR to the extraterrestrial irradiance at the top of the atmosphere is about 0.46 [28]. The solar visible constant is 534.6 W/m2 [29] which is equivalent to the value of PPFDSC of 2443.3 μmol/s/m2.
The definition of sky types (clear, partly cloudy and overcast) is mainly based on the clearness index (kt) (ratio of solar radiation to extraterrestrial solar radiation) (Jacovides, et al. [30-32]). Recently, (Garcia-Rodriguez, et al. [33]) have proposed the CIE (Commission Internationale de L’ ´Eclairage) Standard Sky classification to specify the atmospheric characteristics and illumination levels of each of the established types in terms of energy and daylight. For this purpose, they proposed 15 CIE types of sky conditions.
Several methods are proposed in the literature for modeling of PAR and its derived ratios: a) the radiation transfer models which describe in detail the atmospheric processes (Alados, et al. [19]) b) the artificial neural network c) the estimation through satellite observations [33] and d) empirical models which differ in their complexity and the number of variables involved in the equations. The last category can be subdivided into three groups: i) Simple linear or multilinear models which are based on routinely measured parameters at meteorological stations, such as global radiation, sunshine duration and vapor pressure (Hu, et al. [34]); ii) power law models which are based mainly on clearness index, optical air mass and solar zenith angle (Hu, et al. [35-37]) and iii) empirical models based on selected parameters which affect sky conditions such as the clearness of the sky ((ε) and the brightness of skylight (Δ), global solar radiation, solar zenith angle optical air mass and dew point temperature (Alados et al. [39-40]).
Details about the measurements, quality control and modeling of solar radiation components at the study station are given by Pashiardis and Kalogirou [40]. Furthermore, (Pashiardis, et al. [41]) have studied the characteristics of PAR radiation at Larnaca, a coastal site of Cyprus. (Jacovides, et al. [42]) have extensively studied various aspects of PAR radiation at the inland location of Athalassa, Cyprus, using different types of models.
The first objective of the study is to define the characteristics PAR values through a statistical analysis of hourly and daily values throughout the year and the second objective to implement various models and test them under the prevailing weather conditions at this station. Meanwhile, the levels of PAR were estimated under clear, partly cloudy and cloudy conditions. For this purpose, the clearness index (kt) is used for classifying the sky conditions, i.e., cloudy sky (kt ≤ 0.35), partly cloudy (0.35 < kt < 0.65) and clear sky (kt ≥ 0.65).
Hourly data of global horizontal irradiance (G) were obtained from the automatic weather station of Farmakas, a semi-mountainous location in Cyprus at the height of 833 m, covering the period 2016-2020. For the global radiation measurements, a CM-11 Kipp & Zonen pyranometer is used with an experimental error of approximately 2-3%. Its sensitivity is 8.21 μV/W/m2. For the sunshine duration data a Kipp & Zonen CSD3 sunshine duration sensor is used. The sensor is facing south with a slope (β) of 350 from the horizontal plane. Sunshine duration is defined by WMO as the time during which the direct normal solar radiation exceeds the level of 120 W/m2. The sensor, at the same time, records the direct normal irradiance (Bn) in W/m2. The estimated value is less accurate than the value obtained by the pyrhiliometer which is installed at a solar tracker system (Kipp & Zonen, personal communication). The photosynthetic active radiation is measured with a PAR-LITE Quantum Sensor of Kipp & Zonen and its sensitivity is 5.14 μV/μmol/s m2 with an experimental error of about 5%. This measurement represents the number of photons between 400 and 700 nm incident per square meter per second (Photosynthetic Photon Flux Density, PPFD). The conversion factor of 4.57 μmol/J (or μmol/s /W) proposed by McCree (1972) is used to convert PPFD into its energy alternative (i.e., PARE). All the sensors are factory calibrated. Additionally, the station is equipped with air temperature and relative humidity sensors which are installed at the screen level of 1.2 m above the surface. The station’s coordinates are presented in Table 1. All radiation values were recorded at 1-min intervals, and hourly and daily values are derived from them through integration.
Table 1: Station’s coordinates and mean annual air temperature (Ta), Relative humidity (RH) and annual number of sunshine duration (Sd). 1= Shortest distance from coast in Km.

The average air temperature in summer is about 27 0C while during the winter is about 90C. The maximum air temperature exceeds the value of 40 0C on some days in the summer, while the lowest air temperature reaches -5 0C in winter. The average annual rainfall is about 700 mm and occurs between October and May. The summer season is dry with almost clear sky conditions. Periodically, the island is under the effect of the Saharan Air Layer which is characterized by high content of mineral dust. Dust conditions are more frequent in spring and autumn, although they are also observed in some days in winter and summer. The prevailing wind direction is north-easterly during the day and south to south-easterly during the night. The average annual daily global radiation is 17.5 MJ/m2 and the cumulative annual irradiation is about 6400 MJ/m2. The annual number of sunshine durations is about 2555 hours. About 145 days are considered as clear days. On the other hand, cloudy conditions are recorded in about 45 days.
Radiation Estimations and Quality Control Procedure
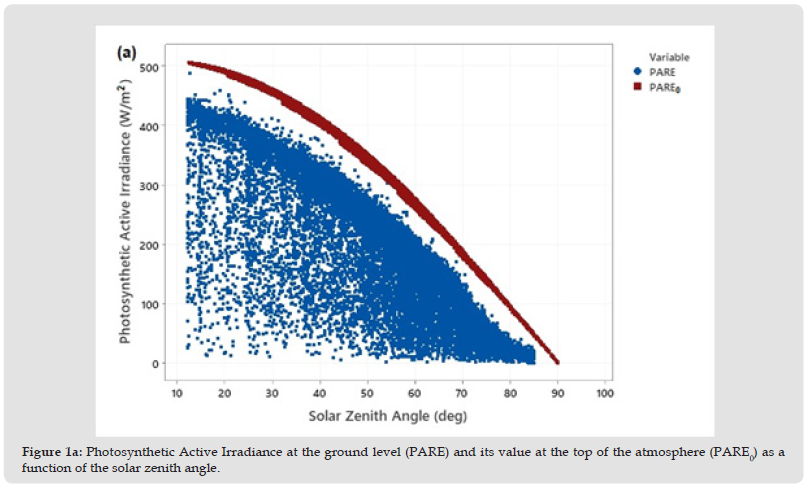
The analysis of this study has been limited to cases in which the solar elevation is higher than 50 due to the cosine response problem. The process of quality control for global and direct normal irradiances and the estimates of diffuse irradiances are described in detail by Pashiardis and Kalogirou [42]. The quality control of shortwave irradiances was based on physical possible, extremely rare and configurable limits, as proposed by BSRN group [43]. Generally, global irradiances (G) are lower than the extraterrestrial irradiances (G0) in the same geographical location. Furthermore, the clearness index (kt=G/G0) should be larger than 0.03 but lower than 1. Similarly, PAR should be smaller than that at the top of the atmosphere for the same geographical coordinates and the daily ratio fFECd (PPFDd/Gd) must be in the range of 1.3-2.8 mol/MJ, otherwise the observation is considered as questionable (Wang, et al. [44]). Both criteria were satisfied as shown in Figure 1. G0 and PARE0 are calculated from the following equations. The irradiance falling on a plain at normal incidence at the top of the atmosphere (G0n) can be estimated from [24]:
Figure 1APhotosynthetic Active Irradiance at the ground level (PARE) and its value at the top of the atmosphere (PARE0) as a function of the solar zenith angle.
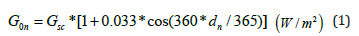
where Gsc is the solar constant for global radiation (1367 W/m2) and dn is the day number of the year (1..365). The respective solar constant for PAR is PARsc= 534.6 W/m2 [45]. Then, the irradiance on a horizontal plain at the top of the atmosphere can be estimated by the following equation:
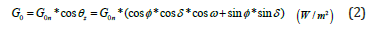
where θz is solar zenith angle, φ is the latitude of the location, δ is the solar declination and ω is the hour angle. The solar declination and hour angles are estimated by the following equations:
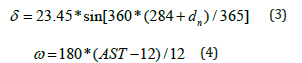
where AST is the apparent solar time for the given day in hours. The local time (t) is converted to solar time (AST) using the following equation:
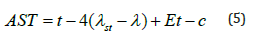
where c is the correction for summer time (c=1 for summer and c=0 for winter), is the reference longitude of the time zone which is positive to the east of Greenwich and for Cyprus is 300, λ is the longitude of the location and Et is the equation of time in minutes which can be estimated from the following equations:
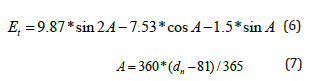
Then, the daily total global irradiation on a horizontal plain at the top of the atmosphere (G0d) is given by:
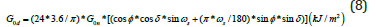
where ωs is the sunset hour angle and is given by:
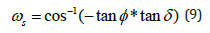
The daily sums of global and PAR are obtained from the hourly values. The quality control process of global and PAR radiation was also extended to their daily values through various range tests. Figure 2 shows that the daily values of global and PAR radiation are within the specified limits. As stated earlier PAR is expressed in terms of either Photosynthetic Photon Flux Density (PPFD) in μmol/s /m2 or in terms of Photosynthetic Active Irradiance (PAR) in W/m2 which is more suitable for energy balance studies. From these terms the following indices can be derived: a) the fractional energy of PARE to global solar radiation (fPAR), b) the fraction of photon flux to energy conversion (fFEC, μmol/J or mol/MJ), i.e., the ratio of PPFD to global radiation and c) the clearness index of PARE, i.e., the ratio of PARE to the extraterrestrial one (PARE0). The above ratios including the clearness index take the following form:
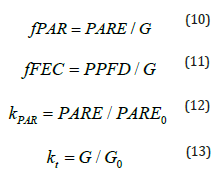
The above ratios can be obtained from both the hourly and daily values. The capital letters and subscripts represent the daily values, while the small letters represent the hourly values. The clearness index (kt) is used for classifying the sky conditions: cloudy sky (kt ≤ 0.35), partly cloudy (0.35 < kt < 0.65) and clear sky (kt ≥ 0.65) (Wang, et al. [46]).
Psychrometric Estimations
The actual water vapor pressure (ea) was estimated by the following equation:

where RH is the relative humidity and es is the saturation vapor pressure estimated by Tetens (1930) formula (Eq. 15) or by Eq. 16, provided by Murray (1967) for temperatures below 0 0C in kilopascal:

where Ta is the air temperature in degrees Celcius. Vapor pressure deficit (VPD) and dew point temperature (Td) were calculated from Eqs. 17 and 18:
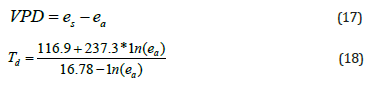
Time Series
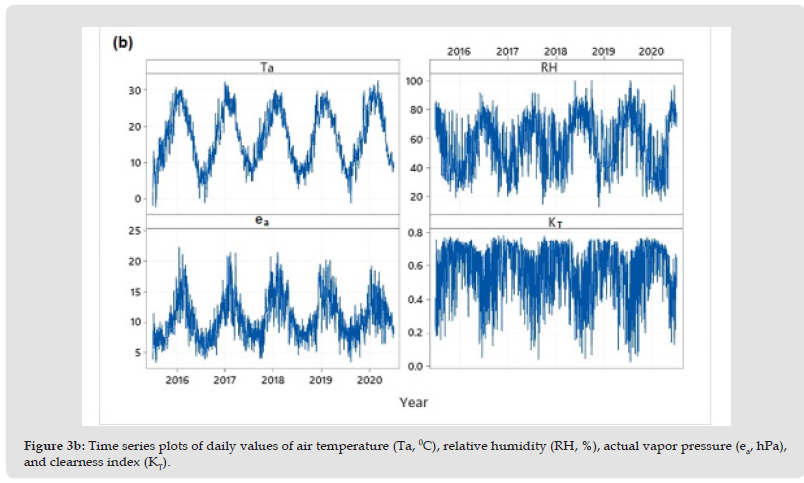
The time series plots of the daily global irradiation and PARE in MJ/m2, as well as the daily PPFD in mol/m2 and the sunshine duration in hrs/d are shown in Figure 3a. The highest values are recorded in the summer and the lowest in winter. The highest daily recorded global radiation is 31.9 MJ/m2, while the highest daily PARE is 12.5 MJ/m2. On the other hand, the highest daily value of PPFD is 57 mol/m2 and the highest sunshine duration is 11.7 hrs/d. The daily variation of air temperature (Ta, 0C), relative humidity (RH, %), actual vapor pressure (ea, hPa) and clearness index (KT) are shown in Figure 3b.
Figure 3A Time series plots of daily global and PARE radiation in MJ/m2, PPFD in mol/m2 and sunshine duration in hrs/d.
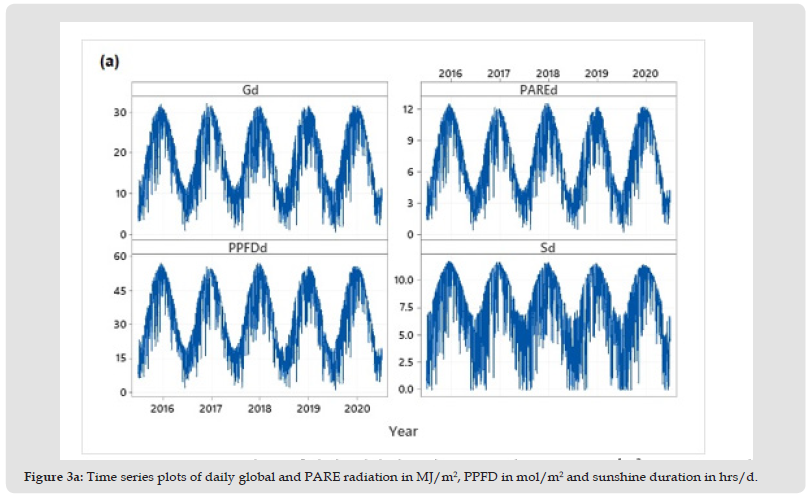
Figure 3B Time series plots of daily values of air temperature (Ta, 0C), relative humidity (RH, %), actual vapor pressure (ea, hPa), and clearness index (KT).
Hourly Values
Seasonal Variability of The Measured and Derived Variables: The monthly means and their standard deviations of the hourly measured and calculated variables are presented in Table 2a. The annual pattern of G and PAR fluctuations presents similar variability. As it can be seen, PARE range between 90 and 225 W/m2, while global irradiances range between 215 and 550 W/m2. The mean annual PPFD is 776 μmol/s/m2 with a seasonal variation between 410 μmol/s/m2 in winter to 1025 μmol/s/m2 in summer. The lowest mean temperatures occur in January and the highest in July ranging from 6.5 0C to 27.2 0C. In contrast, relative humidity ranges between 40% in July to 75% in January. The fraction of PARE to global (fPAR) is relatively constant throughout the year with an annual mean value of 0.412. The monthly means of fFEC range from 1.816 μmol/J in April to 1.914 μmol/J in December with an annual average of 1.881 μmol/J. The clearness indices of global (kt) and PAR (kPAR) are comparable, with kt ranging from 0.370 to 0.595, while kPAR is fluctuating from 0.386 to 0.614. Both air and dew point temperatures (Ta and Td) as well as the vapor pressure parameters exhibit similar patterns with radiation, i.e., higher values in summer and lower values in winter. Based on hourly values, clear skies dominated the sky conditions (40%), followed by cloudy skies (35%) and then partly cloudy skies (25%) (Table 2b& 2a). Monthly means and standard deviations of hourly values of air temperature (Ta, 0C), relative humidity (RH, %), global irradiance (G, W/m2), Photosynthetic Photon Flux Density (PPFD, μmol/s/m2)), Photosynthetic Active irradiance (PARE, W/m2), clearness index of global radiation (kt), clearness index of PAR (kPAR), fraction of PARE to global irradiance (fPAR) and the fraction of photon flux to energy conversion (fFEC) in μmol/J.
Diurnal Variations of Monthly Mean and Maximum Hourly Values: In Figure 4, monthly mean hourly (MMH) values of global and PAR in energy units (PARE, W/m2) and in flux densitiy units (PPFD μmol/s/m2) are shown for Farmakas by means of isoline diagrams. These graphs show representative values of irradiances for each hour of every month of the year. July is the month with the maximum values of both radiation components. At noon, MMH of global irradiance is greater than 700 W/m2, and the PARE irradiance is greater than 380 W/m2. The highest mean hourly of global irradiance in July at local noon is 940 W/m2 and the respective value of PPFD is 1780 μmol/s/m2 (Figures 4d & Figures 4e, respectively). Table 3 presents the maximum hourly values of global and PAR irradiances and the maximum hourly of PPFD fluxes. As it can be seen, the measured maximum hourly global irradiance is 1161 W/m2, while PARE is 488 W/m2 both obtained in July. The highest recorded PPFD value is 2232 μmol/s/m2.
Table 2A: Monthly means and standard deviations of hourly values of air temperature (Ta, 0C), relative humidity (RH, %), global irradiance (G, W/m2), Photosynthetic Photon Flux Density (PPFD, μmol/s/m2))), Photosynthetic Active irradiance (PARE, W/m2)), clearness index of global radiation (kt), clearness index of PAR (kPAR), fraction of PARE to global irradiance (fPAR) and the fraction of photon flux to energy conversion (fFEC) in μmol/J.
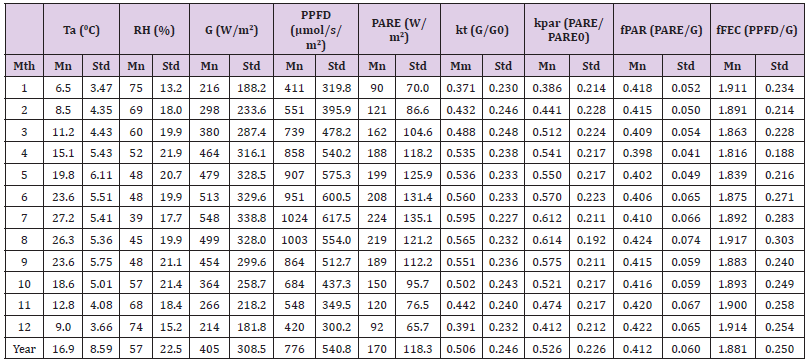
Table 2B: Monthly means and standard deviations of dew point temperature (Td, 0C), saturation vapor pressure (es, kPa), actual vapor pressure (ea, kPa), and vapor pressure deficit (VPD, kPa), along with percentages of cloudy, partly cloudy and clear sky conditions according to the classification of the clearness index (kt).
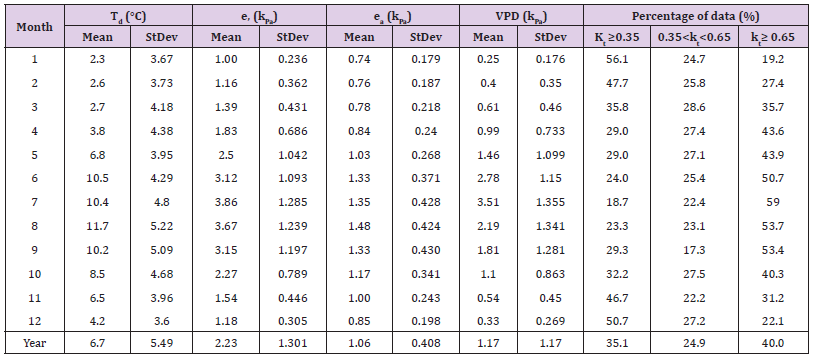
Figure 4 Isoline diagrams of monthly mean hourly of a) global (W/m2), b) PARE irradiance values (W/m2) and c) PPFD flux density values (μmol/s/m2).
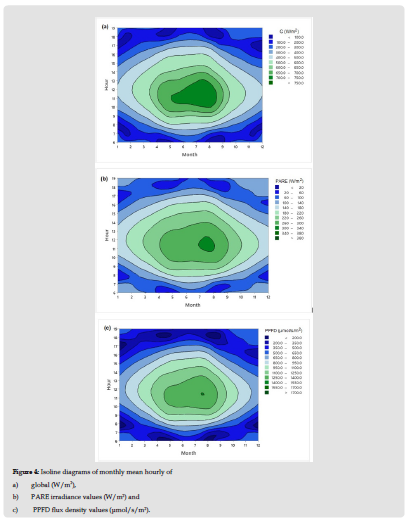
Figure 4E Diurnal evolution of hourly values of Photosynthetic Photon Flux Density (PPFD, μmol/s/m2).
Variability Of Global and PAR Irradiances and The Relevant Indices: The variability of the measured irradiances is demonstrated with the graph of boxplots for each month of the year. The boxplot presents the median and the Interquartile Range (IQR) as well as the outliers (asterisks) of each variable (Figure 5a). The smooth line represents the mean values of irradiances for each month of the year. As it can be seen no outliers are observed for the hourly global and PARE irradiances. The PARE irradiance on clear days is about 50 to 100 W/m2 higher than that under any other weather conditions. The highest variability of all variables is observed in the summer months as it is indicated by the length of the boxes. The variability of clearness indices are shown in Figure 5b. The similarities between the two clearness indices are evident. fPAR and fFEC are relatively constant throughout the year, with an annual mean value of 0.412 and 1.881 μmol/J, respectively. The daily evolution of hourly values of fFEC is shown in Figure 5c. As it can be seen the ratio fFEC is higher in the morning and afternoon hours, while it is more stable during midday. Higher ratios are found under conditions of high cloud cover or higher water content in the atmosphere, a result that supports the findings of various authors (Alados, et al. [19-47]). PAR fraction reaches its highest value during sunrise or sunset and decreases to its lowest values around 08.00 in the morning and around 17.00 in the afternoon. During the rest of the day it is relatively constant throughout the year (Figure 5c). This diurnal rhythm is mainly due to the diurnal cycle of water vapor. Similar results have been reported by (Ho, et al. [46]) in different areas of China.
Figure 5A Boxplots of hourly irradiances in W/m2 and PPFD fluxes in μmol/s/m2 of each month of the year.
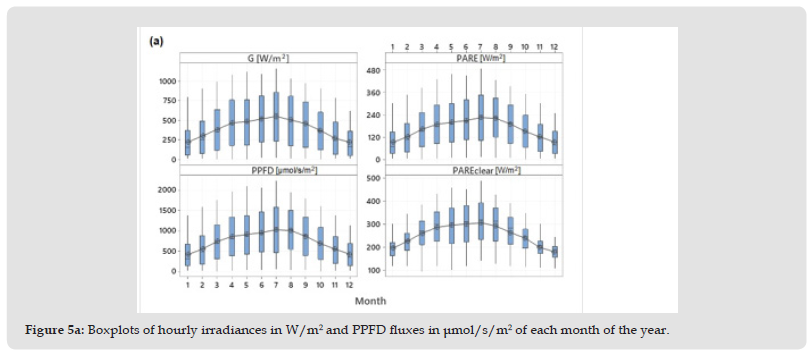
Figure 5B Boxplots of clearness indices of global (kt) and PAR radiation (kPAR) of each month of the year.
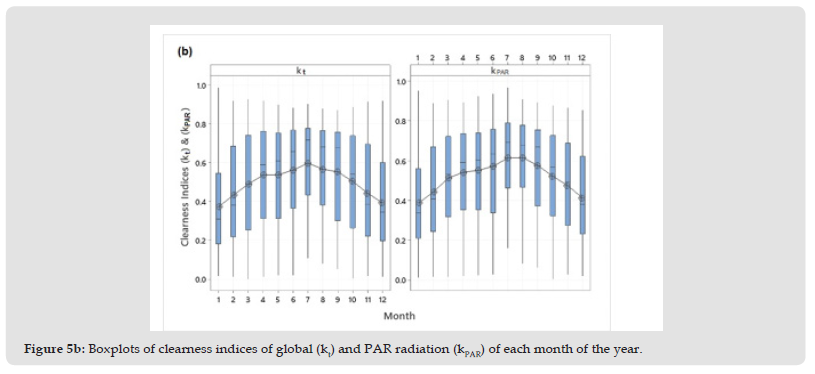
Figure 6A Frequency distributions of hourly values of kt, kPAR, fPAR and fFEC variables at Farmakas during the study period.
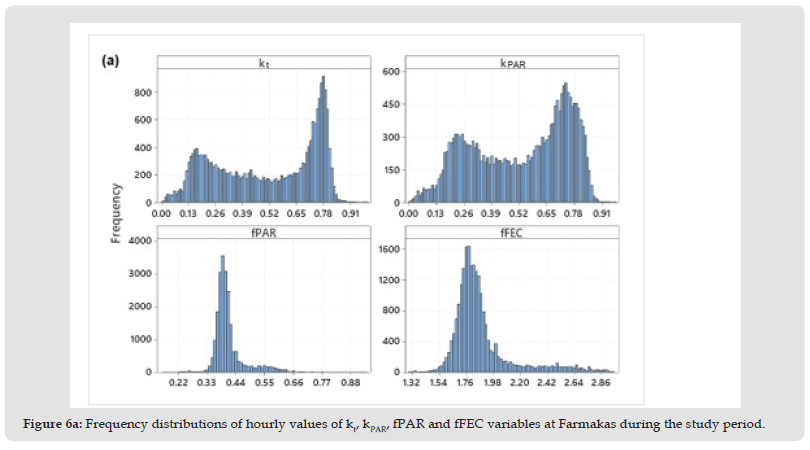
It is known that clouds, gases and aerosols may interrupt the transmission of solar irradiance through the atmosphere; clearness index kt is a general indicator of the absorption and scattering effects and it is used for characterizing sky conditions [46]. Kt was also used for investigating the relationship between PARE and G under various sky conditions in each month. Figure 6a shows the frequency distribution of hourly kt, kPAR, fPAR and fFEC variables at Farmakas during the study period. The pattern of frequency distributions of both clearness indices (kt and kPAR) is almost similar. Regarding the frequency distribution of fFEC, it can be seen from Figure 6a that a larger predominance (71.7%) is observed for the interval of 1.7 μmol/J < fFEC < 2.0 μmol/J, with the largest frequencies (of about 90%) occurring when hourly fFEC was smaller than 2.1 μmol/J. Most of the data (78.2%) were recorded at ea values greater than 0.8 kPa, whereas cases of very low water vapor pressure (ea<0.4 kPa) are very rare (0.5%). The variability of PAR fraction is mainly controlled by the selective scattering of aerosol particles and absorption of water vapor. The annual average of fFEC is 1.756 μmol/J, 1.763 μmol/J and 2.129 μmol/J for clear, partly cloudy and cloudy days, respectively (Figure 6b). The cloudy day’s ratio is therefore about 20% higher than that for clear days and partly cloudy days.
Hourly Relationships: Linear relationships with strong correlations were established between hourly PARE terms and the respective global irradiances:
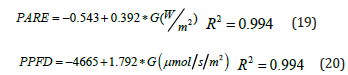
The slopes without the intercepts are 0.391 and 1.789, respectively. The slopes between PARE and G during the winter season vary between 0.381 and 0.384, in spring and autumn they range between 0.385 and 0.391, and in summer they range between 0.392 and 0.398. The monthly slopes of PPFD and G range between 1.742 and 1.760 μmol/J during the winter months and they are higher during the rest of the year ranging from 1.765 to 1.820 μmol/J. The clearness indices also show high correlation:
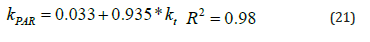
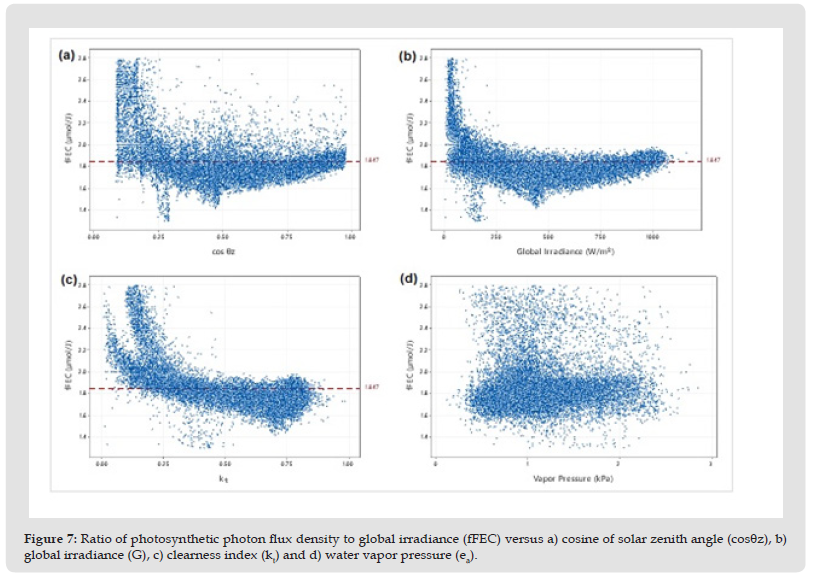
The effect of the solar position, global irradiance, clearness index and actual vapor pressure on the ratio of fFEC (μmol/J) is shown in Figure 7. We can observe that this ratio varies between 1.3 and 2.8 μmol/J with a mean value of 1.847±0.2 μmol/J, and with slightly more scatter for longer path lengths (Figure 7a). Thus, there is no clear dependence of the ratio on solar position, even though the values tend to be higher for solar position close to zenith. Found similar results. A similar picture is observed for the ratio with global irradiance (Figure 7b). Thus, for high values of G, the ratio tends to a value close to its mean value, whereas for low values of G the ratio has high dispersion. A similar picture is obtained with the clearness index (kt), i.e., at cloudy conditions (kt < 0.35) the ratio shows higher values, while at clear conditions the ratio shows less dispersion with values around its mean value (Figure 7c). Finally, there is no relationship between fFEC and actual vapor pressure (Figure 7d). Similar picture is obtained with dew point temperature (Td) (not shown here).
Figure 7 Ratio of photosynthetic photon flux density to global irradiance (fFEC) versus a) cosine of solar zenith angle (cosθz), b) global irradiance (G), c) clearness index (kt) and d) water vapor pressure (ea).
Model Development and Validation: In the literature, there are a lot of empirical or semi-empirical models for estimating PAR using global radiation, air temperature, sunshine hours and other meteorological variables. However, these models are applicable only under the local conditions and extensions of these models to other sites are restricted. Furthermore, some models are only effective in clear skies conditions [47]. Six different models varying in their complexity will be tested. The model accuracy will be evaluated by the scatterplots of the linear relationship between the measured and estimated values. Various statistical indicators, such as the mean bias error (MBE), the root mean square error (RMSE), the relative error (RE) and the coefficient of determination (R2) will be used to assess the accuracy of the models. The estimation of the above indicators are given by the following equations:
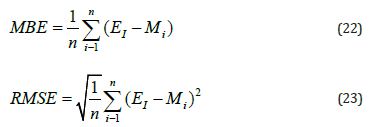
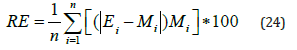
where, Ei is the estimated value, Mi is the measured one and n is the number of observations. The coefficients of the models are estimated using data from the period 2016-2019 (training data set) and their validation is based on the data of the year 2020 (validation data set).
As stated earlier six models different in their complexity will be used to estimate the PAR component. The simplest one is the linear relationship between PPFD and global irradiance (G) (Eq. 25) or “model A‟:
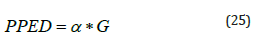
where α is the regression parameter (slope of the line).
Monthly PAR variations reflect those of global radiation (G) (Figure 5). Monthly PAR variations are mainly controlled by seasonal variations of astronomical factors and by fluctuations of meteorological conditions (clouds, water vapor, aerosols, etc.). Numerous studies show that kt can represent the effects of the above factors on the transmission of solar radiation through the atmosphere. Thus, kt is added to improve the accuracy of the estimate (Eq. 26) or “model B‟:
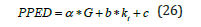
where α, b, c are regression coefficients.
The third model relates the PAR transmissivity (kPAR) with the clearness index (kt) and the relative optical air mass (m). The parameterization model has the following form (Eq. 27) or “model C‟:
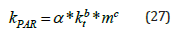
where, α, b, c are regression coefficients. The optical air mass can be calculated from the Kasten and Young (1989) equation as:
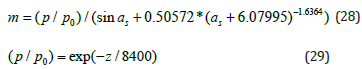
where αs is the solar elevation angle and z is the elevation of the station in m. Figure 8 shows the dependence of hourly PAR on optical air mass (m) under different sky conditions. It is clear that PAR generally decreased with increasing m and the maxima are recorded when sky conditions are clear. A smaller degree of dispersion is evident between PAR values under clear weather and m conditions. The estimation model for PPFDclear takes the following form:
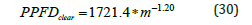
The fourth model, “model D‟ is similar to the third one, but the optical air mass is replaced by the ratio PAR under clear skies to that at the top of the atmosphere (AFclear). The PPDFclear under clear skies is estimated by Eq. (30). Therefore, the model takes the form:
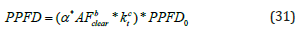
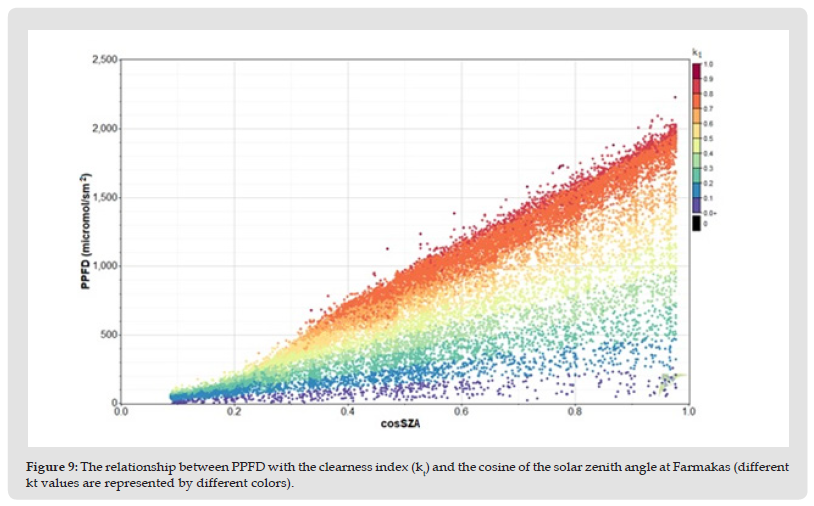
where PPDF0 is the extraterrestrial PAR in units of μmol/s/m2 The fifth model, “model E‟, relates PAR with kt and the cosine of solar zenith angle (μ). Figure 9 depicts the dependence of PPFD on kt and the cosine of solar zenith angle μ. PAR is increased exponentially with increasing μ for a constant kt. The dependence of PPFD on μ is described with a power law equation. Therefore, PAR could be calculated for a narrow kt range with the following equation [44]:
Figure 9 The relationship between PPFD with the clearness index (kt) and the cosine of the solar zenith angle at Farmakas (different kt values are represented by different colors).
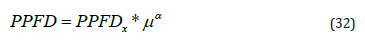
where PPFDx is the maximum PPFD per μ and α describes how PPFD changes with μ. PPFDx is expressed as a function of kt. The estimation of the parameters of the Eq. (26) is done in two steps. Firstly, PPFDx is found by binning of kt in increments of 0.02. Then, the dependence of PPFDx on kt for the training data set (2016-2019) is described by a cubic equation:
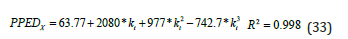
The relationship between PPFD and μ (through α) is investigated using a non-linear regression approach:

Almost similar values were obtained by (Wang, et al. [47]) in Inner Mongolia in China.
The sixth model (model F) was proposed by (Foyo-Moreno, et al. [45]) and is a simple empirical model which estimates PPFD through the expression:
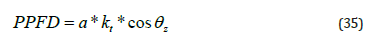
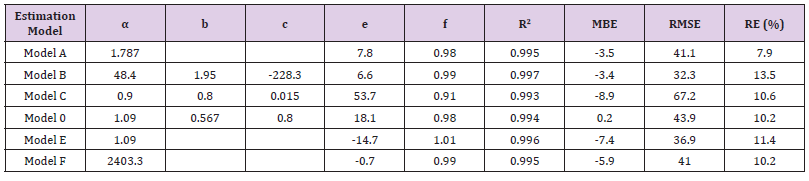
Estimation of the Model’s Parameters: As it is indicated in the previous section, the data set was splited into the training set (2016-2019) and validation data set (2020). The estimated model parameters which are based on the training data set hourly measurements are shown in Table 4. As it can be seen, all models have high coefficient of determination (R2). In all cases, the slopes (f) of the regression lines between the estimated values and the measured ones are close to 1. With the exception of model C all other models show relatively low values of the statistical indicators of MBE, RMSE and RE. Therefore, the simple model A which is based on only one parameter (global radiation) and the empirical multilinear models B and F are essentially the best one (Figure 10).
Table 4: Estimation model parameters (α,b and c) using six different models based on the data set of the period 2016-2019 and the validation was based on the data set of the year 2020. The values e and f represent the intercept and the slope of linear regression between the estimated and measured PPDF variables. R2 is the coefficient of determination. MBE and RMSE are in units of μmol/s/m2.
Daily Values
Seasonal Variation of Daily Global and Photosynthetic Active Radiation: Figure 3a shows the temporal evolution of daily irradiation components at Farmakas. Data reveal a common evolution shape with maxima in summer and minima in winter, due to the daily minimum solar zenith angle and day-length (astronomical factors) variation during the year. Large fluctuations are occurred in spring and autumn during the transition from cold to warm weather and vice versa. As stated earlier, the maximum of daily global solar horizontal irradiation is reached in June or July and it is almost 32 MJ/m2 while the maximum daily PARE is 12.5 MJ/m2. Figure 3b shows also the temporal evolution of the rest meteorological parameters measured at this station. Daily air temperatures range mainly between -2 to 32 0C with an annual mean of about 17 0C. Actual vapor pressure ranges between 3.5 to 22 hPa with an annual daily average of 10.6 hPa. The respective annual mean daily relative humidity is 57%.
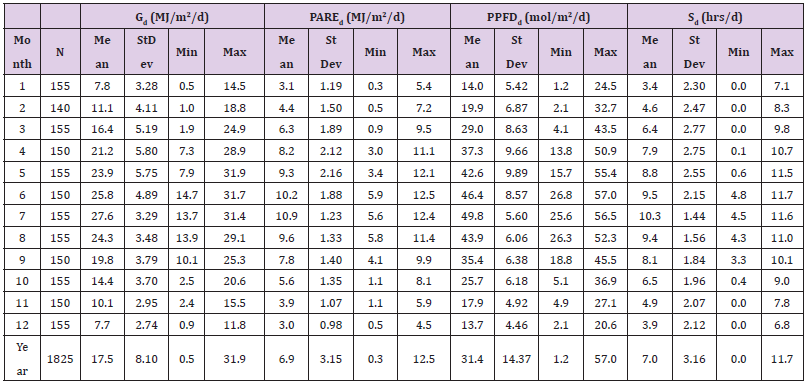
Table 5 shows the mean daily values and their standard deviations of all the radiation components for each month of the year for the whole period of measurements. The variability of the daily values of the global and PAR radiation is also demonstrated through the boxplots of each month of the year (Figure 11). The smooth curve represents the mean daily values of each month of the year. As indicated from the length of the boxplots, the spring season shows the greatest variability. Outliers are observed mainly in July. The monthly mean daily values of the global and PARE radiation components are lower than those obtained at Athalassa and Larnaca (Pashiardis, et al. [47]). The mean daily global radiation ranges from 7.7 MJ/m2 in December to 27.6 MJ/m2 in July with an annual mean daily value of 17.5 MJ/m2. The respective mean daily PAREd ranges from 3.0 MJ/m2 in December to 10.9 MJ/m2 in July with a mean annual value of 6.9 MJ/m2. The mean daily PPFDd ranges from 13.7 mol/m2 in December to 49.8 mol/m2 in July with a mean annual value of 31.4 mol/m2. The highest daily value of PPFDd is 57.0 mol/m2. The frequency distribution of the above variables is presented in Figure 12a, while the cumulative density functions (CDF) are demonstrated in (Figure 12b&12a) shows that the distribution of all variables is almost similar. Figure 12b indicates that in 75% of the year, the daily sums of global irradiation is less than 24.5 MJ/m2, less than 9.5 MJ/m2 for PARE, less than 43.5 mol/m2/d for PPFD and less than 10 hrs/d for sunshine duration.
Figure 10 A comparison between estimated and measured PPFD in μmol/s/m2 based on validation data set using model A.
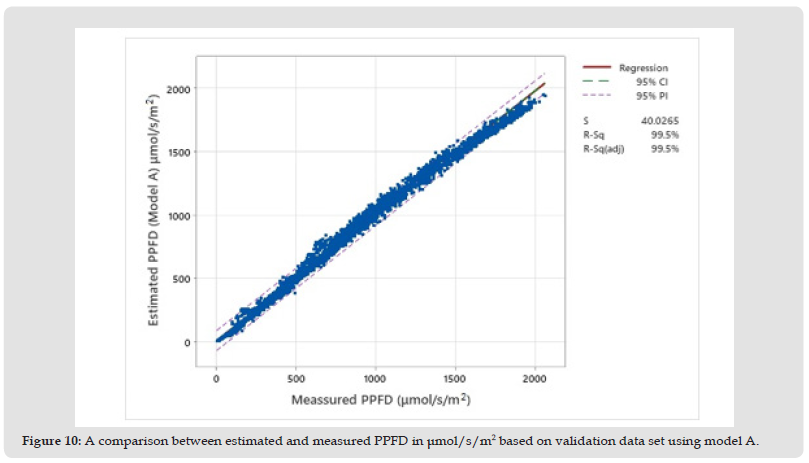
Figure 11 Boxplots of daily Global (Gd) and PAREd in MJ/m2 , daily PPFDd in mol/m2 /d and sunshine duration (Sd) in hrs/d for each month of the year. The smooth line represents the mean daily values of each month for each variable
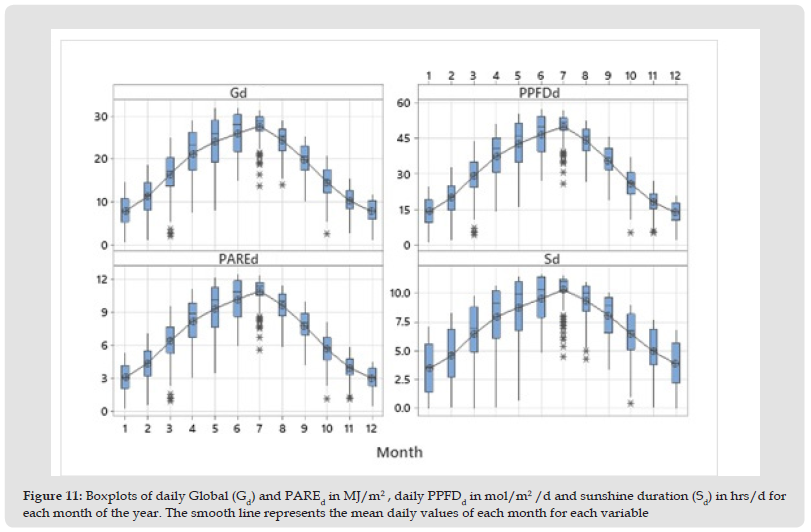
Figure 12A Frequency distribution of daily values of global (Gd), PAREd, PPFDd and sunshine duration (Sd) at Farmakas.
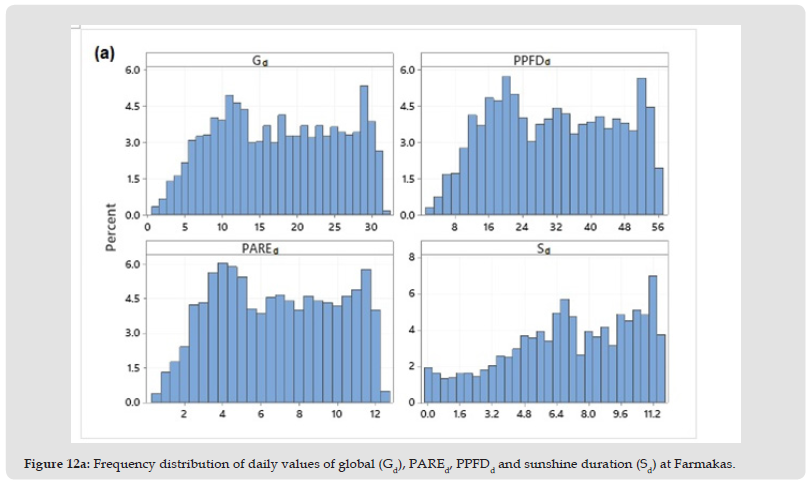
Figure 12B Cumulative density function (CDF) of global(Gd), PAREd, PPFDd and sunshine duration (Sd) at Farmakas
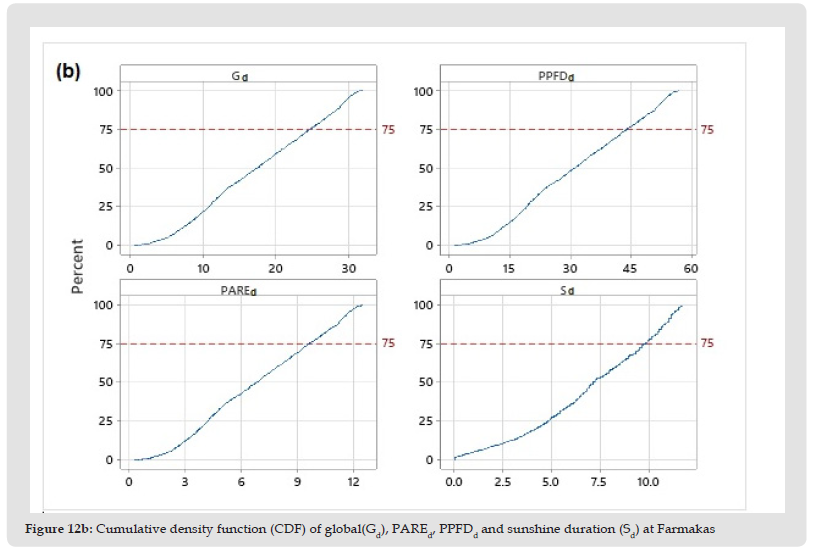
Table 5: Mean daily statistics of global, PARE components for each month of the year and for the whole period of measurements (MJ/m2) as well as monthly mean daily sunshine duration in hrs/d.
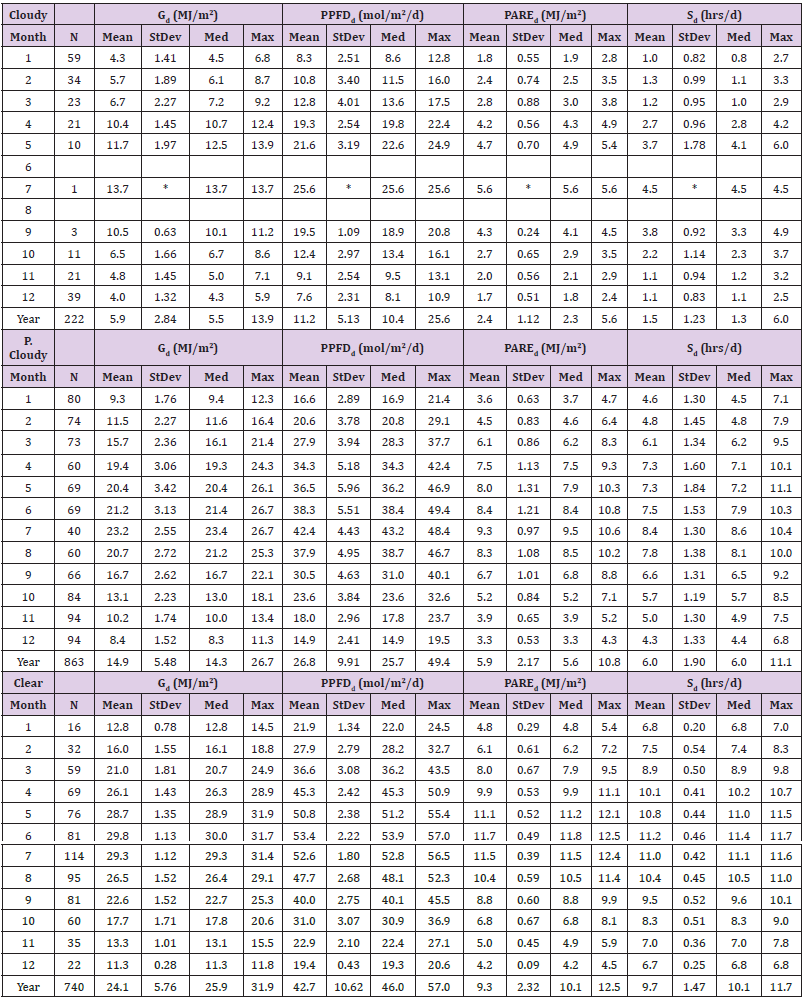
Daily Clearness Index and Relative Sunshine Duration: The clearness index (KT), for a particular time interval, is defined as the ratio of the global radiation to the extraterrestrial radiation. It is an objective measure of the influence of cloud cover on the solar radiation flux. As it was indicated earlier three different classes are defined according to the values of the daily clearness index. The variation of the daily clearness index throughout the year is shown in Figure 13. It is clear that in summer months there are no cloudy days. The monthly statistics based on the daily clearness index values for Farmakas are reported in Table 6. Also listed in the table is the number of days according to the above classification for each of the month of the year. The annual average of KT is 0.565 with a standard deviation of 0.161. The average values of the daily clearness index range between 0.423 in January to 0.679 in July. The annual number of cloudy days is 44.4 (12.16%), the respective number for partially cloudy days is 172.6 (47.29%) and 148 days are classified as clear days representing the 40.55% of the annual number of days. As it can be seen the summer months are classified mainly as clear days. The results of the partition of the daily global, PARE radiation and sunshine duration values on the basis of the corresponding KT values (i.e., the criteria for classifying day type) are reported in Table 7. The annual mean of PAREd is 2.4 MJ/m2 for cloudy conditions, 5.9 MJ/m2 for partly cloudy and 9.3 MJ/m2 for clear sky conditions. The respective annual mean daily values of PPFDd are 11.2 mol/m2, 26.8 mol/m2 and 42.7 mol/m2. The annual daily average of sunshine duration is 7.0 hours with an annual total of 2555 hours. The monthly mean daily values range between 3.4 hours in January to 10.3 hours in July. The maximum daily value is 11.7 hours and it occurs in the summer months. The site is exposed to an average of about 57% of daily sunshine over the year.
Table 6: Monthly statistics of daily clearness index and number of days (N) according to the classification for each month of the year.
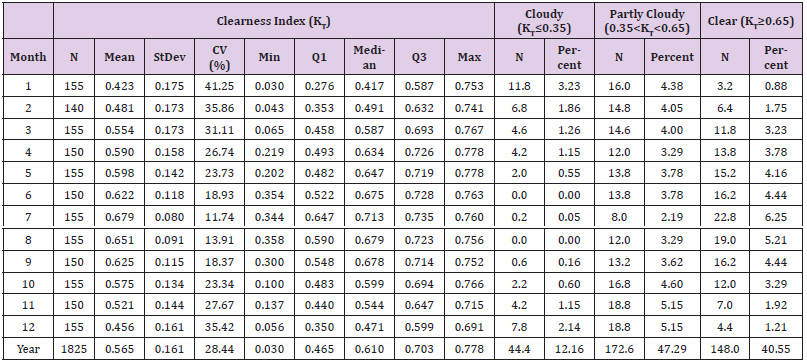
Table 7: Monthly statistics of daily global (Gd) (MJ/m2), PAREd radiation (MJ/m2), Photon Photosynthetic Flux Density (PPFDd) (mol/m2) and sunshine duration (Sd) (hrs/d) for clear, partially cloudy and cloudy days at Farmakas. N is the number of days according to the above classification for the period of measurements.
The relationships of daily PAR radiation (PAREd) and Photon Photosynthetic Flux Density (PPFDd) with the daily global and sunshine duration are shown in the following equations. PARE radiation and global radiation are linearly related, while for the daily sunshine duration a second degree polynomial is used (Figure 14). All relationships have high coefficients of determination:
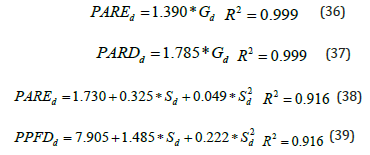
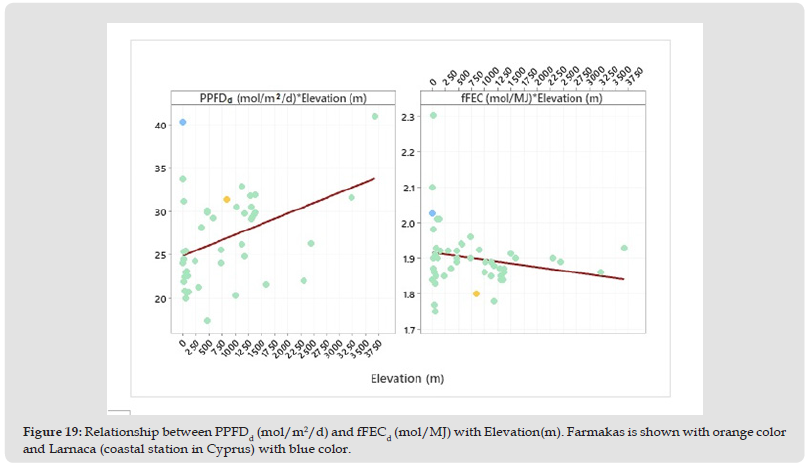
Seasonal Variation of Daily PAR Indices: The time series plots of the daily PAR and global radiation indices are shown in Figure 15. KPAR and KT show a similar pattern with the highest values occurring in the summer months. In contrast, fPAR and fFEC have their highest values in the winter months. The descriptive statistics of daily PAR indices for the three classes of sky conditions are presented in Table 8. The annual mean of KPAR increases from 0.266 for cloudy conditions to 0.703 for clear sky conditions. Similarly, the relative sunshine duration (σd) increases from 0.132 to 0.764. In contrast, fPARd decreases from 0.419 for cloudy conditions to 0.387 for clear sky conditions. A reduction is also observed for the fraction of photon flux density to energy conversion (fFECd). It decreases from 1.913 mol/MJ under cloudy conditions to 1.768 mol/MJ under clear sky conditions. This reduction is clearly illustrated in Figure 16. A similar graph is obtained between fFECd and relative sunshine duration (σd). Daily KPAR is closely related with the clearness index (KT) and relative sunshine duration (σd):
Figure 13 Daily clearness index (KT) for each day of the year. The reference lines indicate the thresholds for the classification of the days according to the value of KT.
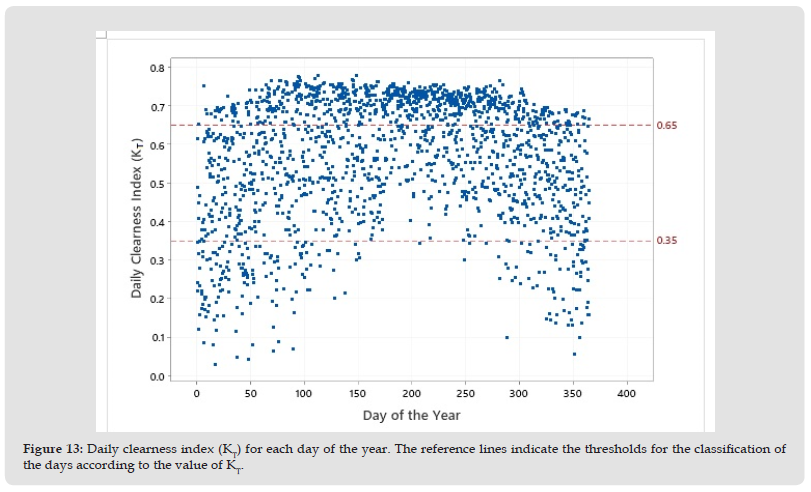
Table 8: Descriptive statistics of daily PAR clearness index (KPAR), fraction of PAR to global radiation (fPARd), fraction of photon flux to energy conversion (fFECd) and relative sunshine duration (σd) under cloudy, partly cloudy and clear sky conditions for each month of the year.

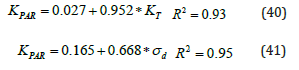
The variability of all the daily indices is shown in Figure 17. The maximum of KPAR and KT are recorded in the summer months, while fPAR and fFEC are relatively constant throughout the year with the highest values occurring in the winter months. Outliers are also recorded mainly in the winter months. The frequency distributions of the above daily indices are shown through the histograms in Figure 18a. KPAR and KT show an exponential distribution, while fPAR and fFEC show an approximately normal distribution with mean values of 0.394 and 1.799 mol/MJ, respectively. The respective standard deviations of the said variables are 0.014 and 0.065 mol/MJ. The cumulative frequency curves of the above variables are presented in Figure 18b. The reference line of 75% percentile is also shown. In 75% of days KPAR and KT are less than 0.695, fPAR is less than 0.400 and fFEC is less than 1.830 mol/MJ. The frequency distribution of fFECd for each classification type of sky conditions is shown in Figure 18c. It is clear that in cloudy conditions fFECd is higher than under clear conditions.
The altitude dependency of the average annual values of daily PPFDd and fFECd was checked with the help of the relevant values from a number of stations around the world. Figure 19 shows that PPFDd is increased with elevation while fFECd is relatively constant with a very weak correlation. The slope is closed to zero and it is not significant at the 5% level. The values of Farmakas are closed to the regression lines.
Figure 18C Frequency distributions of fFECd for each classification type according to sky conditions.
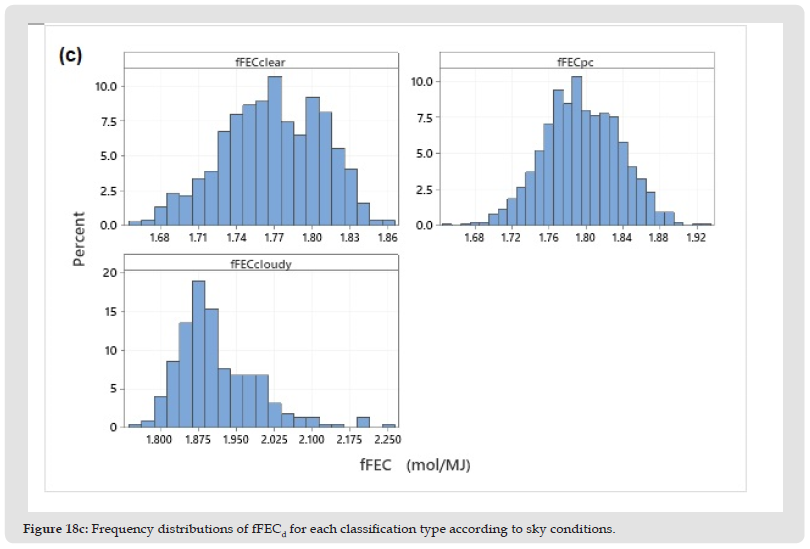
Figure 19 Relationship between PPFDd (mol/m2/d) and fFECd (mol/MJ) with Elevation(m). Farmakas is shown with orange color and Larnaca (coastal station in Cyprus) with blue color.
Hourly data of global horizontal irradiance (G) and photosynthetic active radiation (PAR) were obtained from the automatic weather station of Farmakas, an inland location in Cyprus at the height of 833 m, covering the period 2016-2020. A CM-11 pyranometer is used for the measurement of global radiation in W/m2 and a PAR-LITE Quantum Sensor for the measurement of PPFD flux in μmol/s/m2. For the sunshine duration measurements, a Kipp & Zonen CSD3 sunshine duration sensor is used. The sensor, at the same time, measures the direct normal irradiance (Bn) in W/m2. PAR is either expressed as Photosynthetic Photon Flux Density (PPFD) in units of μmol/s/m2 or in power units (PARE, W/m2) which is more suitable for energy balance studies. From these units the following derived indices are calculated: (a) the fractional energy of PAR to global radiation (fPAR), (b) the fraction of photon flux energy conversion fFEC in μmol/J for the hourly values and mol/MJ for the daily values and (c) the clearness index of PAR (kPAR) i.e., the ratio PAR to the extraterrestrial one. Furthermore, these indices are related to the clearness index (kt) which is the ratio of global radiation to the radiation at the top of the atmosphere. The first objective of the study is the quality assessment of the measured radiation components. For this purpose, the data were undergone an extensive quality control process for both the hourly and the daily values, which were then statistically analyzed including their derived indices. The BSRN tests showed that the data are within the specified limits. The second objective of the study refers to the modeling of PAR radiation using six models which differ in their complexity.
Monthly mean daily PPFDd increased from 13.7 mol/m2/d in December to 49.8 mol/m2/d in July with annual mean value being 31.4 mol/m2/d. Monthly mean daily fFECd increased from 1.77 mol/MJ in April to 1.83 mol/MJ in January with annual mean value being 1.80 mol/MJ. Similar values are obtained in most parts of the world. It was also discovered that partly cloudy skies (47.3%) were the dominant conditions which are followed by clear sky conditions (40.5%). Only 12.2% are considered as cloudy skies. Generally, fFECd is decreased from 1.91 mol/MJ under cloudy conditions to 1.77 mol/MJ under clear sky conditions, which is due to the strong absorption and scattering effects of clouds on longer wavelengths. Similarly, fPAR is decreased from 0.419 under cloudy conditions to 0.387 under clear sky conditions. The annual average of daily clearness index (KT) is 0.565 with a standard deviation of 0.161. Hourly values of global and PAR irradiances are shown by means of isolines diagrams. These values are considered representative of the solar radiation behavior along a typical year and can be useful for exploiting solar energy applications. Seasonal analysis allows in highlighting the difference between summer and winter irradiation conditions. Six models different in their complexity are used to estimate the PAR component. The simplest one was a linear relationship between PPFD and global irradiance, while the second and the sixth are multiple regression model based on global irradiance and clearness index and the cosine of solar zenith angle. The rest three models use power law equations based mainly on clearness index, optical air mass and cosine of solar zenith angle. The model coefficients were obtained from the four years ‘training data set’ (2016-2019) and the performance of the model was tested against the ‘validation data set’ of the year 2020, using the most popular statistical methods such as mean bias error (MBE), root mean square error (RMSE), relative percentage error (RE) and the coefficient of determination (R2). The estimated parameters were close to those obtained by (Hu, et al. [41]) in the North China plain. All models have high coefficient of determination. In all cases, the slopes of the regression lines between the estimated values and the measured ones are close to 1. With the exception of model C all other models show relatively low values of the statistical indicators of MBE, RMSE and RE. Therefore, the simple model A which is based on only one parameter (global radiation) and the empirical multilinear models B and F are essentially the best one.
The annual average daily global radiation intensity is around 17.5 MJ/m2, whereas PARE is 6.9 MJ/m2. The monthly mean daily values for the global radiation range between 7.5 and 27.5 MJ/m2 while for PARE radiation they range between 3.0 and 10.9 MJ/m2. The maximum of daily global solar horizontal irradiation is reached in June or July and it is almost 32 MJ/m2. The daily maximum of PARE irradiation is 12.5 MJ/m2. The annual daily average sunshine duration is 7.0 hours with an annual total of 2555 hours. The monthly mean daily values of sunshine duration range between 3.4 hours in January to 10.3 hours in July. The maximum daily value is 11.7 hours and it occurs in the summer months. The site is exposed to an average of about 57% of daily sunshine over the year. The monthly mean daily relative sunshine duration ranges between 0.35 in January to 0.73 in July. This work has specifically contributed to the characterization and analysis of hourly and daily solar photosynthetic active radiation and there derived indices.
The authors would like to thank the Meteorological Department of Cyprus for providing the solar radiation data used in this study.


