Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Francisco Casesnoves*
Received: September 12, 2022; Published: September 22, 2022
*Corresponding author: Francisco Casesnoves, PhD Engineering, MSc Medical Physics, Physician. Independent Research Scientist. International Association of Advanced Materials, Sweden. Uniscience Global Scientific Member, Wyoming, USA
DOI: 10.26717/BJSTR.2022.46.007337
Continuing with Anisotropic Analytic Model (AAA) for Wedge Filters (WF) photon- dose delivery series, this contribution moves ahead with implementation of those AAA studies of WF formulation/simulations into Biological Models-significantly developed by other authors in the literature. Results comprise the WF dose delivery 3D simulations for approximate tumor clonogenes population survival rate. Solutions of previous 3D photon-dose delivery numerical/imaging simulations for AAA model 18 Mev photon-beam, depth-doses [ z=5,15 cm], habitually breast tumors depth-dose magnitudes, and 15° WF are set into fundamental Linear Quadratic Bio model equation. Developments of Linear Quadratic Bio models are mathematically/statistically presented—focused on methodology and imaging software, accuracy is not the main objective at this stage. Results for 2D variation of parameter [α] related to N0 values are proven. A new statistical/probabilistic modification for the Linear Quadratic Bio model for software adjustment is presented. Software and programming methods for BM were achieved. Results of 3D Graphical Software for this Bio model implementations are shown. Findings involve the mathematical-computational method explanations to work up and implement a photon-dose model into a final survival-rate biological one. Applications on Clinical Radiotherapy Physics and Radiation Oncology for breast cancer treatment are described in brief.
Abbreviations: MM: Mathematical Methods; BM: Biological Models; LQM: Linear Quadratic Model; IE: Integral Equation; TCP: Tumor Control Probability; TCCP: Tumor Control Cumulative Probability; RPD: Radiation Photon-Dose; Nonlinear Optimization, Series Approximations, Radiotherapy Treatment Planning Optimization; SSD: Source- Surface Distance ; Software Engineering Methods, Radiation Photon-Dose, AEF: Attenuation Exponential Factor; Nonlinear Optimization; WF: Wedge Filter; AAA: Anisotropic Analytic Model; FF: Fluence Factor; OF: Omega Factor; TPO: Treatment Planning Optimization; BT: Breast Tumor
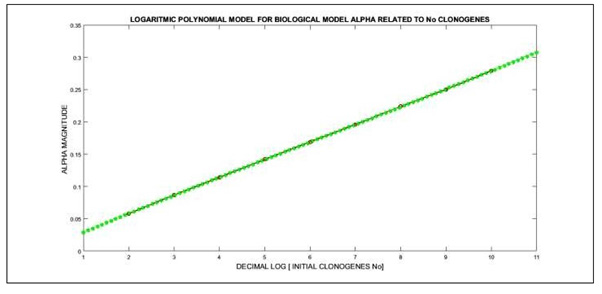
Following the Radiation Therapy research series, [1-20], this stepping-up study objective is the implementation of AAA extensive previous publications results into Biological Models (BM) TPO parameters. Development for 3D Graphical Optimization solutions from recent study [19] to obtain Tumor Clonogenes Survival Rate NS constitutes the purpose of this research. Photon-beam Biological Models are based mainly on exponential functions with radiobiological parameters, namely [ α, β], whose magnitudes are determined in general with in vitro experimental [21-24]. The Photon- beam Model applied for getting these objectives is AAA Model [1-20]. Second practical purpose of the article is to set Photon-dose delivery magnitudes, modified by Wedge Filters (WF), for dosedepths useful in Breast Cancer TPO. That is, [ z= 5,15 cm, for 18 MeV] are usual dose delivery depths in breast tumors, modified to conform its shape with WF. Thus, Radiation Dose is implemented within the BM exponential-equation to determine the TPO dose optimized by the proper radiosensitivity characteristics of the tumor [21-24]. In consequence, the photon-dose magnitude can be also used for statistical methods to determine probabilistic parameters such as Tumor Control Probability with distributions like Poisson or Binomial. Hence, TCP can be got though convolution of TCP with Gaussians depending on radiobiological parameters [ α, β]. Breast cancer BM parameters have been experimentally determined in the literature because the incidence/prevalence in developed countries of this tumor increase gradually [25]. The research results present two main strands. First is a group of BM new algorithms for NS Rate determination. Secondly 3D Graphical Optimization and Numerical Calculations of NS Rate from these equations at delivery dose depths [ z= 5,15 cm, for 18 MeV]. Results magnitudes coincide with other contributions datasets [21-24]. Additionally, a polynomial fit numerical equation graph for variation of parameter [α] related to N0 values [data for software from [23], Table 44.2)] was obtained, Figure 1. Succintly, 3D Graphical Optimization methods with imaging processing and BM based on NS Rate are presented specifically for breast cancer radiotherapy TPO applications.
Section is divided into several sub-sections. In brief, from Bio model formulations and new model [19], to techniques for implementation of photon-dose delivery AAA Model into Linear Quadratic Bio model. The basic AAA WF dose delivery formulas and numerical data for [ z= 5, 15 cm] depths are reminded from previous publications [refs]. The statistical-probabilistic approximations to develop a Tumor Control Probability Integral Equation Model are explained [19,21-24].
Bio models’ equations are not very complicated, and based usually on exponential functions, statistical distributions, and two radio sensitivity key parameters, namely [α and β biological modelling parameters]. An Integral Equation Model (IEM), based on new Linear Quadratic Model and Statistical Binomial Distribution approximation was published in recent contributions [19]. The simplest Linear Quadratic model equation set in [19,21-24] reads.
Elementary Biological Model for clonogenes survival population Ns;s
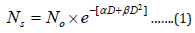
Where,
Ns: Initial number of tumors clonogens
No: Surviving number of tumors clonogens α: Clonogen radiosensitivity parameter
β: Clonogen radiosensitivity parameter D: Total radiation dose delivered
Parameters [α and β] have interrelated each other [β/α] and to N0 magnitude. Parameter [α] is related to N0 magnitude [ ref], although an average value is generally implemented. Both [ α and β] measurements are taken in vitro [19,21-24]. Equation (1) is more complicated in practice for a number of constraints. Firstly, the dose D is hypofractionated in clinical practice [19,21-24]. Secondly, a Lea-Catcheside function-factor K [21], has to be introduced. However, fractional dose factors, d, and number of fractions n, [21-24], are omitted in (1) for simplification, and are not relevant for the mathematical method development. In the standard BM research, [19,21-24], the quotient [ σ/β] is generally considered constant. In this study, however, alpha and betha radiosensitive parameters are set independently. The reason is avoiding too many approximations. By using 100% percentages and 1% rates for N0,s, the model can be better implemented in Statistical Distributions to obtain TCP formulation, [19], with Poisson, Binomial, and Normal-Gaussian distributions. By using this modification, [Casesnoves, 2022], several numerical inconvenient are sorted. This variant, using percentages and rates of N0 implies to make calculations setting parameters [α, mainly, and β] values in function of N0, for example [23, Table 44.2 ] . Figure 1 shows an original numerical equation from these values [23]. Thus, [ 19], the modified BM equation reads.
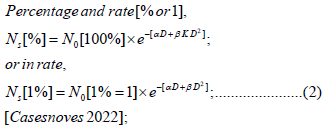
where
Ns: Initial number of tumors clonogens
No: Surviving number of tumors clonogens α: Clonogen radiosensitivity parameter
β: Clonogen radiosensitivity parameter D: Total radiation dose delivered
K: Lea-Catcheside function-factor K, [21]
This approximation, Equation (2), facilitates further calculations and evolved models. However, setting percentages and/or rates for N0 is conditioned for the magnitude changes of [α, β] related N0 [23], Table 44.2], Figure 1.
Figure 1: Numerical equation graph for variation of parameter [ α] related to N0 values [data for software from [23], Table 44.2, ( Mayles, W ; Nahum, A) ]. Model [green] is the straight line, numerical experimental data [red] match almost perfectly the model line. Errors and Residual Norms are almost null. However, it can be considered an approximation because numerical data published is subject to several constraints [23]. The increment of [ α] parameter when N0 rises is sharply demonstrated.
The large number of basic formulas reminder from [1-20], are described in Table 1 to explain the first implementation into 3D programs to get finally the Survival Rate NS data. Exclusively for illustration, main implemented Photon-Dose Equations from [1- 20]. Also from [19,21-24], dose-depth [ z=5], numerical data from [19] appropriate for breast cancer irradiation is shown Tables 2 & 3. Depth Dose Equations for [ z=15 cm ] can be found at [1-8]. Those all [ z=5, 15 cm] cover the approximate TPO range from a small mammary glands size to a bigger one. Essential algorithms reminders are presented in Equations 3,4. The most important reminder algorithms from [1-20], for photon-dose implementation into the BM read.
Table 1: Most AAA references formulation along radiotherapy series studies with foundations and corrections by other authors. All data for [ z= 5 cm] dose delivery parameters published at [20].
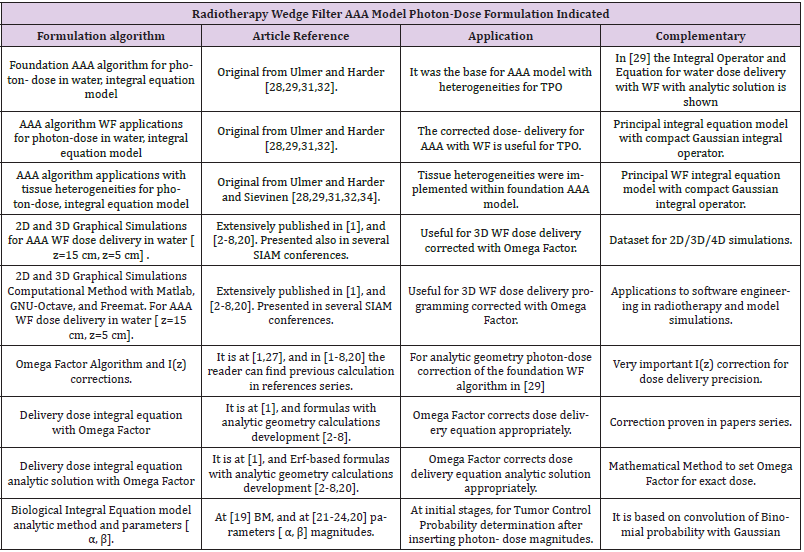
Table 2: AAA model main Photon-Beam Spectra parameters for 3D Graphical simulations. Dataset is large, it is recommended to consult references [1-8, 20,26-29].
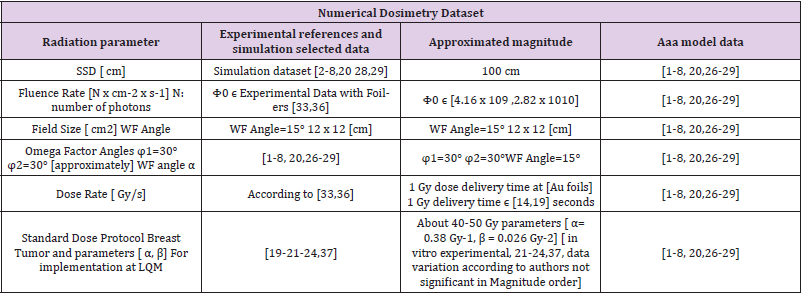
Table 3: From [72], AAA model main Photon-Beam computational equations parameters for 3D Graphical simulations [ z= 5 cm], [ 1-8,20].

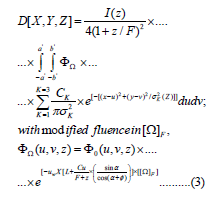
where I(z) is the area integral of the dose over a plane perpendicular to the z-axis at depth z, normalized to one incident electron, σ (z) is the depth-dependent mean square radial displacement, x, y, z are the coordinates of the dose-delivery point at beam-output coordinates system, u, v, z, are the coordinates of photon-fluence at depth z, a, b, are the field-size magnitudes at depth z, CK are optimization parameters resulting for a triple Gaussian function setting, Φ0 is the photon fluence source for WF ; a’(z) =a(l + z/F), b’(z) =b(1 + z/F) are the half side lengths projected into depth z, with F as the source-surface distance (SSD). Parameters μw (WF material parameter), α (WF angle) and φ (photon-beam divergence angle) are defined at [1-8,26-29]. The WF manufacturing angle is α. C is the distance in z-coordinate from source to WF surface, L is half-length of WF for y coordinate. In general, Fluence modification is ΦU = Φ0 / (1 + z/F)2 according to [28,29]. Then source fluence is Φ0 modified primarily for the dose- delivery depth z and secondly by the WF parameters [1-8,26-29]. And the solution, exact, complete, geometrically corrected with Omega Factor, and analytical of this integral equation [Casesnoves, 2015, April, Philadelphia], reads.
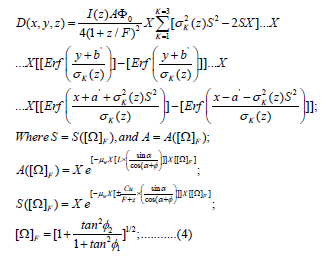
where A and S parameters are defined at formulas according to a series of parameters. I(z) is the area integral of the dose over a plane perpendicular to the z-axis at depth z, normalized to one incident electron, σ (z) is the depth- dependent mean square radial displacement, x, y, z are the coordinates of the dose-delivery point at beam-output coordinates system, u, v, z, are the coordinates of photon- fluence at depth z, a, b, are the field-size magnitudes at depth z, CK are optimization parameters resulting for a triple Gaussian function setting, ΦU is the photon fluence modified for WF, a’(z) =a(l + z/F), b’(z) =b(1 + z/F) are the half side lengths projected into depth z, with F as the source-surface distance (SSD). Parameters μw (WF material parameter), α (WF angle) and φ (photon-beam divergence angle) are defined at [1-8, 26-29]. The WF manufacturing angle is α. C is the distance in z-coordinate from source to WF surface, L is half-length of WF for y coordinate. In general, Fluence modification is ΦU = Φ0 / (1 + z/F)2 according to [28,29], and ΦU = Φ0 / (1 + z/F)2 according to [28,29]. Then source fluence is Φ0 modified primarily for the dose-delivery depth z and secondly by the WF parameters [1-8, 26-29]. Parameters μw (WF material parameter), α (WF angle) and φ (photon-beam divergence angle) are defined at [1-7,9-15,17,30,31]. Development of Equations 1-4 are extensively presented in [1-8,28,29]. The angles Φ1 and Φ2 are the geometrical angles for Omega Factor computation defined [1- 8]. Constants are given following the previous equations. This formula is an Omega Factor correction from the equations of classical AAA model [28,29,32,33]. The S and A variables depend on Omega Factor and were mathematically developed in previous numerical computation programming and 3D Graphical simulations [ 1-20].
Table 2 presents BM parameters for complete determination of SR of the BM based on [19,21-24] algorithms, IEM and algebraic calculations. Table 3 shows AAA photon-dose parameters calculations for first optimization step, based on from [1-20]. The most important parameters to be implemented within programming are: approximate Photon Fluence Rate [N x cm-2 x s-1], and approximate Delivery Dose per second [ Gy x s-1]. These data are calculated with experimental dosimetry from the literature for 18 Mev [27,34]. 18 Mev Photon Beam Spectrum dataset is taken form experimental literature [27,34]. Once the Photon-Dose delivery is determined, the magnitude is implemented within BM. Thus, the numerical development/ design of the 3D simulations programs is rather difficult. Table 2 also shows approximations that were applied for all calculations at software. Table 2 AAA model main Photon-Beam Spectra parameters for 3D Graphical simulations. Dataset is large, it is recommended to consult references [1-8,20,26-29,34,35]. The first calculation and program implementation are the AAA photon-dose (3-4). The second part involves implementation of photon-dose into BM algorithm for calculation of NS Rate by using (1-2) algorithms [36,37]. The patterns design of Matlab programs are rather arduus to obtain acceptable results approximations.
Breast tumors (BT) incidence and prevalence has increased significantly in recent decades [19,20,25,38,39], especially in developed countries. Epidemiology statistics [25], by year 2013 show these approximated data,
1) Breast cancer: about 11% of all tumors.
2) Europe shows an approximate incidence of 90 per 100,000 women in Western Europe [25].
3) Developed world zones [25]: higher (greater than 80 per 100,000).
The most frequent statistical anatomical place for BT growth is the superior-external quadrant of mammary glands. In that case, it is also frequent when the tumor is palpable, [25,38,39] to find ganglia tumoral invasion at corresponding axilla. Therefore, TPO depth parameter z=5 cm is appropriate in general for small mammary glands, while z=15 cm approximation is convenient for bigger mammary glands and/or internal tumor invasion. That is the TPO simulations justification for simulation parameters in this study [25,38,39]. Constant medical exploration, and self-exploration constitutes the first simple method for early detection [25,38,39]. Total dose protocol for TPO in breast cancer is about [40,41] Gy, with variations from country, institution to country, institutions, Cancer Care Centers [25,38,39].
Following the previous mathematical development, Tumor Control Cumulative Probability (TCCP) was determined in a new Integral Equation Model (IEM) [19] Equation (5). The usual Poisson Distribution for the TCP, [21-24], was approximated to a Binomial Distribution to obtain an analytic solution of the TCCP integral equation published in [21]. This method starting point was based on previous BM contributions [21-24]. As detailed in [19], the IEM for TCCP reads.
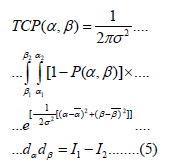
Where
α: Clonogen radiosensitivity integral parameter β: Clonogen radiosensitivity integral parameter
σ: Approximated standard deviation both for α, β parameters I1: First Gaussian integral, Normal Distribution
I2: Second Probability Function Gaussian convolution with Binomial Distribution α1: Inferior 2D IE limit
α2: Superior 2D IE limit β1: Inferior 2D IE limit β2: Superior 2D IE limit
P (α, β): Binomial Probability function for Convolution
All the development of this IEM and analytic determination with Erf functions is explained in [19]. Analytical solution of this IEM at [19].
The programming method(s) used for this study are based in a high number of previous papers [1-20]. For BM, new advances and programs were required. Table 4 shows the techniques and software improvements to obtain better calculations, 3D processing images, error determinations, and get applied exactly the new/ modified BM model formulas/algorithms.
Table 4: AAA model main parameters for 3D Graphical simulations [1-20]. Program software parts numerically calculated for Equations 1-4 with new corrections. The data from Tables 1-3 was implemented.

The 3D Graphical Optimization of NS Rate is shown in Figures 1-6 for [ z= 5,15 cm, 18 Mev]. The Numerical results are presented in Table 5 (Figure 2-7).
Figure 2: Matlab NS Rate simulation 3D image for 18 Mev photon-beam at 5 cm depth-dose with Omega Factor and I(z) corrected. The delivery time shot is 1 second. Matrices for Image Processing have about [300 x 300] elements. Imaging Processing Method 1. At figure, inset, axes interval modifications explained.
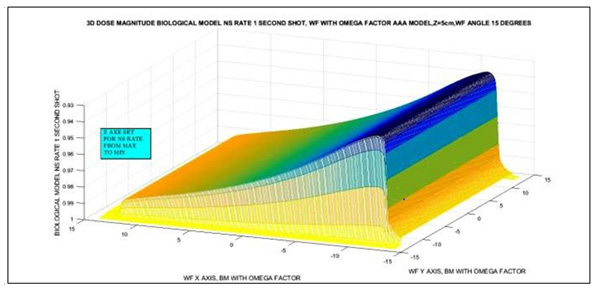
Figure 3: Matlab NS Rate simulation 3D image for 18 Mev photon-beam, 5 shots, at 5 cm depth-dose with Omega Factor and I(z) corrected. The delivery time shot is 1 second. Matrices for Image Processing have about [300 x 300] elements. Imaging Processing Method 1.
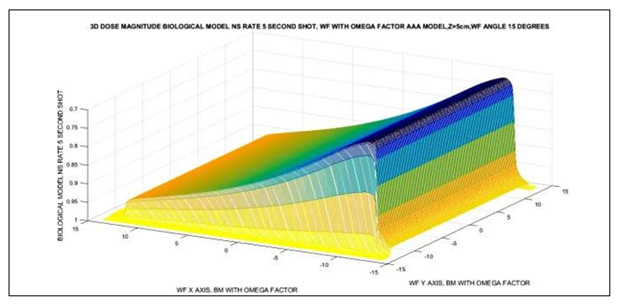
Figure 4: Matlab NS Rate simulation 3D image for 18 Mev photon-beam, 10 shots, at 5 cm depth-dose with Omega Factor and I(z) corrected. The delivery time shot is 1 second. Matrices for Image Processing have about [300 x 300] elements. Imaging Processing Method 1.
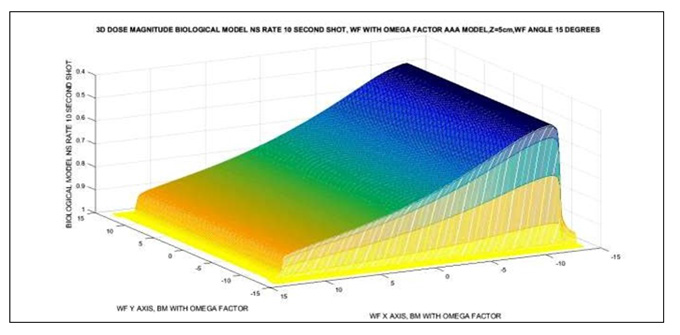
Figure 5: Matlab NS Rate simulation 3D image for 18 Mev photon-beam, 1 shot, at 15 cm depth-dose with Omega Factor and I(z) corrected. The delivery time shot is 1 second. Matrices for Image Processing have about [300 x 300] elements. Imaging Processing Method 1.
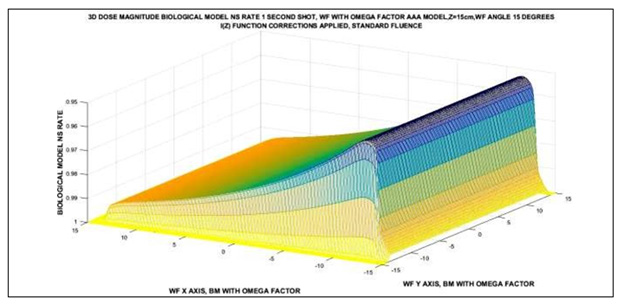
Figure 6: Matlab NS Rate simulation 3D image for 18 Mev photon-beam, 15 shots, at 5 cm depth-dose with Omega Factor and I(z) corrected. The delivery time shot is 1 second. Matrices for Image Processing have about [300 x 300] elements. Imaging Processing Method 1.
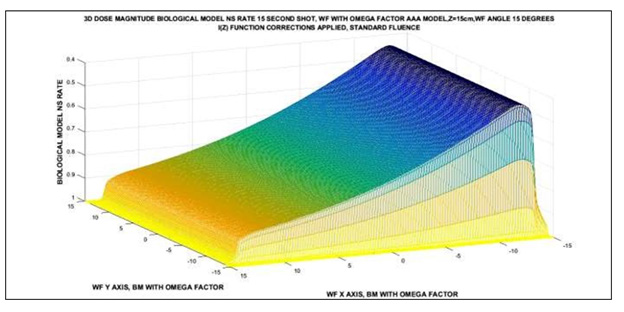
Figure 7: Matlab NS Rate simulation 3D image for 18 Mev photon-beam, 10 shots, at 5 cm depth-dose with Omega Factor and I(z) corrected. The delivery time shot is 1 second. Matrices for Image Processing have about [300 x 300] elements. Imaging Processing Method 1. Inset, explanations for Maximum and Minimum NS Rates.
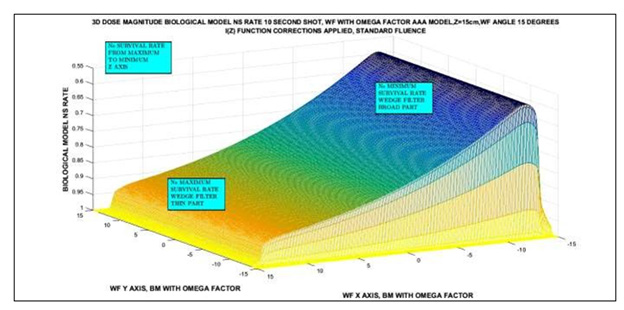
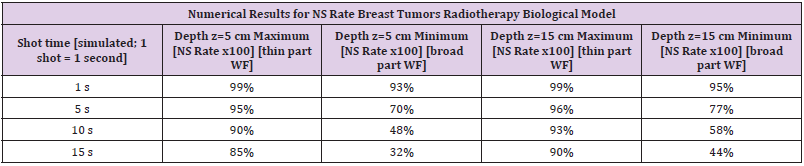
Table 5 shows a resume of breast tumor medical physics principal applications for radiotherapy TPO. Those prospective applications are also useful for radiotherapy research/applications on breast tumors and other types of cancer (Table 6).
Table 5: Brief of Numerical results for Survival Rate. Results agree with literature, e. g., [ Figure 10.1 and others, [22]. Matlab 3D image processing data.
The objective of the research was to apply algorithms from [20] to get NS acceptable 3D and numerical simulations for breast cancer rutinary photon dose depths [ z= 5, 15 cm]. The photon dose parameters were presented extensively in publications series [1-20]. The results are a series of 3D Graphical Optimization sets with NS Rates for those parameters. Numerical and Graphical data obtained is agree closely the experimental of literature [21-24]. Biomodel parameter NS Rate agrees to experimental dataset in the literature [64-67] with approximations. The 2D polynomial approximation for [α] variation related to N0 magnitude results be fine. Advantages of this method are accuracy in 3D determination of NS and easy method from the presented models to calculate Clonogenes Survival Rates for breast tumors. Inconvenient, for example, are the experimental variation of [ α] parameter related to N0, Figure 1. The results are calculated for AAA model in water without tissue heterogeneities corrections. However, mammary gland overall density is close to water one. Grosso modo, new BMs algorithms were presented with formulation, numerical and 3D Graphical Optimization results. Appropriate applications for breast cancer TPO come up from all the solutions obtained.
IEM was developed by Dr F Casesnoves on 15th March 2022. All initial equations were developed from previous researchers’ contributions [21-24]. The NS initial integral formulas were published in [21-14]. From those equations, all the mathematical development is original from the author [1,20]. This article has previous papers mathematical techniques, [1-18], whose use was essential to make IE model analytic solution, approximations, and NS Rate and Probability Function. Table 3 is understanding reader’s essential from [20], and Equations 12-4 also. The complete mathematical development will be carefully reviewed/checked in subsequent publications. The number of Dr Casesnoves publications at references is intended also for reader’s learning. When editors permit, references are ordered in subsequent rationale arrangement. This study was carried out, and their contents are done according to the European Union Technology and Science Ethics. Reference, ‘European Textbook on Ethics in Research’ [37,42-44]. European Commission, Directorate-General for Research. Unit L3. Governance and Ethics. European Research Area. Science and Society. EUR 24452 EN [42- 4460-63]. And based on ‘The European Code of Conduct for Research Integrity’. Revised Edition. ALLEA. 2017 [37,42-44]. This research was completely done by the author, the calculations, images, mathematical propositions and statements, reference citations, and text is original from the author. When a mathematical statement, proposition or theorem is presented, demonstration is always included. If any results inconsistency is found after publication, it is clarified in subsequent contributions. The article is exclusively scientific, without any commercial, institutional, academic, religious, religious-similar, non-scientific theories, personal opinions, friends and/or relatives’ favors, political ideas, or economical influences. When anything is taken from a source, it is adequately recognized. Ideas and some text expressions/sentences from previous publications were emphasized due to a clarification aim [37,42-72].
Dr Francisco Casesnoves earned the Engineering and Natural Sciences PhD by Talllinn University of Technology (started thesis in 2016, thesis Defence/PhD earned in December 2018, official graduate Diploma 2019). Dr Casesnoves is European Union and Internationally qualified as Doctor in Engineering to supervise PhD Theses, Master Theses, and Bachelor Theses in science and engineering. He works as independent research scientist in computational engineering/physics. Dr Casesnoves earned MSc-BSc, Physics/Applied-Mathematics (Public Eastern-Finland-University, MSc Thesis in Radiotherapy Treatment Planning Optimization, which was developed after graduation in a series of Radiation Therapy Optimization-Modelling publications [2007-present]). Dr Casesnoves earned Graduate-with-MPhil, in Medicine and Surgery [1983] (Madrid University Medicine School, MPhil in Radioprotection Low Energies Dosimetry [1985]). He studied always in public-educational institutions, was football player 1972-78 (defender and midfielder) and as Physician, supports healthy life and all sports activities. Casesnoves resigned definitely to his original nationality in 2020 for ideological reasons, democratic-republican ideology, ethical professional reasons, anti-state monarchy corruption positions, and does not belong to Spain Kingdom anymore. His constant service to the International Scientific Community and Estonian technological progress (2016-present) commenced in 1985 with publications in Medical Physics, with further specialization in optimization methods in 1997 at Finland-at the moment approximately 100 recognized publications with approximately 65 DOI papers. His main branch is Computational-mathematical Nonlinear/ Inverse Methods Optimization. Casesnoves best-achievements are the Numerical Reuleaux Method in dynamics and nonlinear-optimization [books 2019-2020], The series of Radiotherapy Improvements for AAA superposition-convolution model, the Graphical and Interior Optimization Methods [2016-8], the new Computational Dissection-Anatomical Method, [2020], invention of Forensic Robotics [2020-2021], and Molecular Effect Model for High Temperature Superconductors [2020]. Dr Casesnoves PhD thesis is an Estonian scientific service to European Social Fund and several EU Research Projects. Dr Casesnoves scientific service since 2016 to the Free and Independent Republic of Estonia for technological development (and also at Riga technical University, Power Electrical and Electronics Department) is about 40 physics-engineering articles, two books’ series, and 1 industrial radiotherapy project associated to Europe Union EIT Health Program (Tartu University, 2017).


