ABSTRACT
Diffusion caused by electric currents and the Hall effect can lead to a formation of chemical inhomogeneities in plasma. This mechanism can be responsible for a formation of chemical spots in laboratory and astrophysical plasmas. Such diffusion can be accompanied by a very special type of magnetohydrodynamic waves in which only the number density of impurity oscillates. These waves can be called compositional waves. They exist if the magnetic field is sufficiently strong and the magnetic pressure in plasma is much greater than the gas pressure. Keywords: multicomponent plasma, magnetic field, linear waves, chemically peculiar vortices.
Keywords: Multicomponent Plasma; Magnetic Field; Linear Waves; Chemically Peculiar Vortices
Introduction
Often laboratory and astrophysical plasmas are
multicomponent, and diffusion of elements is important for some
phenomena. For instance, diffusion processes can lead to chemical
inhomogeneities and, as a result, to change the emission, heat
transport, and conductivity [1-3]. In thermonuclear fusion, the
source of impurities is usually the chamber walls, and diffusion
determines the distribution impurities [4-6]. Even a small number
of heavy ions influences the rate of radiative losses in plasma
and changes its thermal properties. In astrophysical conditions,
chemical inhomogeneities have been detected in the surface layers
of many stars of various spectral types. It is widely accepted that
these inhomogeneities are determined by diffusion processes but,
however, the mechanisms resulting information of chemical spots
is still uncertain. Diffusion in plasma can differ qualitatively from
that in neutral gases because of the presence of charged particles
- electrons. This particularly concerns hydrogen plasma [7]. In
such plasma, the influence of electrons on diffusion of heavy ions is
especially pronounced.
Chemical inhomogeneities can appear because of various
reasons, for instance, it is often thought that chemical spots occur
due to the presence of magnetic fields. The magnetic field B can
magnetize electrons and produce a non-uniform distribution
of ions. Anisotropy of transport is characterized by the Hall
parameter, xe =ωBeτ where 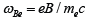 is the gyrofrequency
of electrons and τe is their relaxation time. In hydrogen plasma,
is the gyrofrequency
of electrons and τe is their relaxation time. In hydrogen plasma, 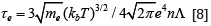 where n and T are the number density and temperature of electrons, respectively, L is the Coulomb
logarithm. The current-driven diffusion can lead to a formation of
chemical inhomogeneities like other diffusion processes. Using
a simple model, we show that the interaction of the current and
field with impurities leads to their diffusion in the direction
perpendicular to both. This type of diffusion can contribute to
formation of chemical spots even in a relatively weak magnetic field
with xe << 1. We also show that such diffusion can be accompanied
by a particular type of waves in which only the impurity number
density oscillates.
where n and T are the number density and temperature of electrons, respectively, L is the Coulomb
logarithm. The current-driven diffusion can lead to a formation of
chemical inhomogeneities like other diffusion processes. Using
a simple model, we show that the interaction of the current and
field with impurities leads to their diffusion in the direction
perpendicular to both. This type of diffusion can contribute to
formation of chemical spots even in a relatively weak magnetic field
with xe << 1. We also show that such diffusion can be accompanied
by a particular type of waves in which only the impurity number
density oscillates.
Formulation of the Problem and Basic Equations
Consider a cylindrical magnetic configuration with the field
in a z-direction, 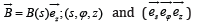 are cylindrical coordinates and the corresponding unit vectors. Then, the electric
current is given by
are cylindrical coordinates and the corresponding unit vectors. Then, the electric
current is given by

If jϕ → 0 at large s then B→ B0 =const at s→∞. Note that such magnetic configurations can be unstable for some dependences B(s) [9-11] but we assume that the instability does not occur for chosen dependencies B(s). Plasma is assumed to be fully ionized and consists of electrons e, protons p, and small amount of heavy ions i. A small admixture of heavy ions does not influence the dynamics of a background hydrogen plasma and these ions can be considered as test particles. The partial momentum equations in ionized plasma have been discussed by [7,12]. The paper [12] considers transport processes in the hydrogen-helium plasma but the derived equations describe the hydrogen plasma with a small admixture of heavy test ions. Then, the partial momentum equation for ions i has the form
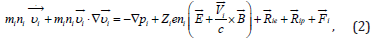
where 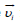 is the velocity, Zi is the charge of the species i, pi and ni
are the partial pressure and number density, respectively, and
is the velocity, Zi is the charge of the species i, pi and ni
are the partial pressure and number density, respectively, and 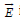 is
the electric field;
is
the electric field; 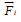 is the external force on species i. We neglect the
external force in our model since its influence is often insignificant.
The forces
is the external force on species i. We neglect the
external force in our model since its influence is often insignificant.
The forces 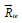 and
and 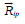 are caused by the interaction of ions i with
electrons and protons, respectively. The forces
are caused by the interaction of ions i with
electrons and protons, respectively. The forces 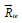 and
and 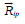 are
internal and their sum over all components is zero.
are
internal and their sum over all components is zero.
The velocity 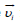 can be represented as a sum of
can be represented as a sum of  and
and 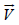 where
where  is the hydrodynamic velocity of plasma and ~V i is a diffusive
velocity of ions i relative plasma. Since in our model ni is small
compared to np, the hydrodynamic velocity is approximately equal
to the mean velocity of protons,
is the hydrodynamic velocity of plasma and ~V i is a diffusive
velocity of ions i relative plasma. Since in our model ni is small
compared to np, the hydrodynamic velocity is approximately equal
to the mean velocity of protons, 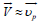 . In this paper, we assume that
background plasma is in hydrostatic equilibrium. Then,
. In this paper, we assume that
background plasma is in hydrostatic equilibrium. Then, 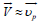 = 0 and, hence,
= 0 and, hence, 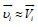 . If the temperature is uniform, the friction force
. If the temperature is uniform, the friction force
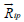 has only a component proportional to the relative velocity of
ions i and protons,
has only a component proportional to the relative velocity of
ions i and protons, 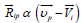 . This force can be easily calculated
if Ai = mi /mp >>1. Since the velocity of a background plasma is zero,
. This force can be easily calculated
if Ai = mi /mp >>1. Since the velocity of a background plasma is zero, 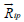 can be represented as
can be represented as

[12], where 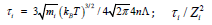 is the
characteristic time of scattering between protons and heavy ions; L
is assumed to be the same for all types of scattering.
is the
characteristic time of scattering between protons and heavy ions; L
is assumed to be the same for all types of scattering.
The friction force on the l.h.s of Eq. (2), 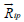 , can be estimated as
, can be estimated as
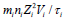 and the first term in this equation is
and the first term in this equation is  where
Dt is the timescale of diffusion processes. Therefore, this term is
much smaller than the friction force
where
Dt is the timescale of diffusion processes. Therefore, this term is
much smaller than the friction force 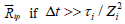 . The
second term on the l.h.s. of Eq. (2) is of the order of
. The
second term on the l.h.s. of Eq. (2) is of the order of 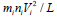 where
L is the characteristic length scale. Since L ~ Vi Δt , this term can also
be neglected if
where
L is the characteristic length scale. Since L ~ Vi Δt , this term can also
be neglected if 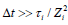 . Then, Eq. (2) transforms into
. Then, Eq. (2) transforms into
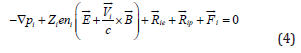
If ni << np , then, 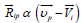 is given by
is given by 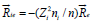 [12], where
[12], where 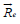 is the force acting on the electrons. Since ni<< n,
is the force acting on the electrons. Since ni<< n, 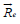 is determined
by scattering of electrons on protons but scattering of electrons on
heavy ions gives a small contribution. Therefore, one can use for
is determined
by scattering of electrons on protons but scattering of electrons on
heavy ions gives a small contribution. Therefore, one can use for 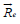 the expression obtained by [7] for one-component plasma. In the
case of a cylindrical isothermal configuration, this force reads
the expression obtained by [7] for one-component plasma. In the
case of a cylindrical isothermal configuration, this force reads

where 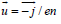 is the velocity of electric current;
is the velocity of electric current; 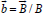 ; coefficients α ⊥ and α ∧ have been calculated by Braginskii [7]. The
force (5) is caused a friction due to a relative motion of the electron
and proton gases. Then, Eq.(1) yields for the current velocity
; coefficients α ⊥ and α ∧ have been calculated by Braginskii [7]. The
force (5) is caused a friction due to a relative motion of the electron
and proton gases. Then, Eq.(1) yields for the current velocity 
Consider the current-driven diffusion in a magnetic field with
xe <<1 . Substituting 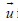 into Eq.(5) and using coefficients α ⊥, ∧ we
obtain with the accuracy in linear terms in xe
into Eq.(5) and using coefficients α ⊥, ∧ we
obtain with the accuracy in linear terms in xe
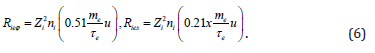
The momentum equation for the species i (Eq.(4)) depends on s E and Eϕ components of the electric field. The momentum equations for e and p, containing these electric fields, read

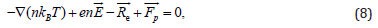
Using Eq. (5), we obtain

Substituting Eqs.(6), (3), and (9) into the s- and ϕ -components
of Eq.(4), we arrive to the expression for a diffusion velocity,  ,
,

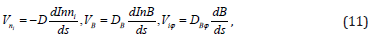
Vni is the standard diffusion velocity and VB is the velocity of diffusion caused by the current. The corresponding diffusion coefficients are
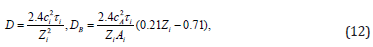

where 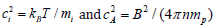 .
.
Distribution of Ions Under the Influence of Electric Currents
The condition of hydrostatic equilibrium reads in our model

where p and r are the total pressure and density of plasma, respectively. In hydrogen plasma, we have p ≈ 2nkB T where kB is the Boltzmann constant. Integrating Eq. (14) and assuming the temperature to be constant, we obtain

where 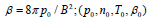 are the values of (p, n, T, b) at
s → ∞.
are the values of (p, n, T, b) at
s → ∞.
Consider the distribution of elements in equilibrium. Since Vis = 0 in equilibrium, Eq.(10) yields

The r.h.s. is responsible for the influence of currents on the distribution of impurities. One has from Eq. (16)

Taking into account Eq. (16) and integrating Eq.(17), we have

where μ = − 2Zi (0.21Zi− 0.71) and ni0 is ni at s →∞. If the local abundance of i is γi = ni/ n , then taking into account Eq. (17), obtain

where γi0 = ni0 /n Local abundances depend essentially on the field strength. These dependences are particular sensitive to B in the case of heavy ions with large charge numbers. If other diffusion mechanisms are negligible, then the exponent (μ − 1) reaches large negative values for large Zi and, as a result, strong abundance anormalies can be produced in this case. For instance, (μ − 1) is equal 1.16, -0.52, and -2.04 for Zi =2, 3, and 4, respectively. Note that (μ − 1) changes its sign with an increase of Zi : (μ − 1) > 0 if Zi = 2 but (μ − 1) < 0 for Zi ≥ 3. Therefore, elements with Zi ≥ 3 are in deficit (γi <γi0 ) in the region with a weak magnetic field (B < B0) but these elements should be overabundant in the region with a stronger field, B > B0.
Eq. (20) describes the distribution of impurities in diffusive equilibrium. The characteristic timescale to reach this equilibrium, tB, can be estimated as

where L is the length scale of the magnetic field, L = |d In B/ds|-1 . The characteristic timescale of baro-diffusion is given by the wellknown expression

Hence, the current-driven diffusion operates on a shorter timescale if DB > D or
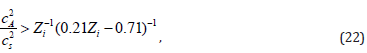
where cs is the sound speed, 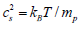 . Therefore, the
current-driven diffusion is more efficient if the magnetic pressure
exceeds the gas pressure.
. Therefore, the
current-driven diffusion is more efficient if the magnetic pressure
exceeds the gas pressure.
Chemical Vortices
In our simplified model of cylindrical magnetic configuration and velocity (10), the continuity equation for ions i has the form
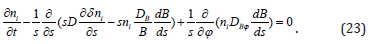
Consider the behaviour of small perturbations of ni by making use of a linear analysis of Eq. (23). In the unperturbed state, we assume that plasma is in a diffusive equilibrium and, therefore„ the unperturbed impurity number density satisfies Eq. (18). For the sake of simplicity, we assume that small perturnations are independent of z. Denoting disturbances of the impurity number density by i δ n and linearizing Eq.(23), we obtain the equation that describes the evolution of such small perturbations,
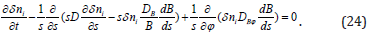
Consider only disturbances with a short radial wavelength. If
this wavelength is shorter than the length scale of unperturbed
quantities, then we can use the so-called local approximation. Then
small disturbances are α exp(−iks)where k is the radial wavevector,
ks >>1. Since the basic state does not depend on time and ϕ
, perturbations can be represented in the form  where m is the azimuthal wavenumber and ω should be calculated
from the dispersion equation. Such disturbances have a shape of
cylindrical vortices of a chemical composition. Substituting i δ n into
Eq. (24), we derive the dispersion equation for such perturbations
in the form
where m is the azimuthal wavenumber and ω should be calculated
from the dispersion equation. Such disturbances have a shape of
cylindrical vortices of a chemical composition. Substituting i δ n into
Eq. (24), we derive the dispersion equation for such perturbations
in the form

This dispersion equation describes a special type of
magnetohydrodynamic waves where only the number density of impurities oscillates. Note that there are many different sorts
of waves in magnetized plasma that can produce oscillations of
a chemical composition. Such oscillations, for example, can be
generated by standard magnetohydrodynamic waves [12] but,
usually, fluctuations of impurities in such waves are accompanied by
fluctuations of other hydrodynamic quantities. Indeed, the electric
field has actively to take part in such waves and interact more
efficiently with heavily charged ions than with protons. As a result,
MHD waves can produce fluctuations of a chemical composition.
However, these fluctuations are typically very small because the
period of MHD waves is much shorter than the diffusion timescale.
Chemical fluctuations become significant only if the period of a
wave is comparable to the diffusion timescale.
The waves considered in this paper are caused by diffusion
processes and their period is generally comparable to the diffusion
timescale. Therefore, fluctuations of a chemical composition
can reach a significant value in such waves. The quantity ωR is
responsible for decay of these waves with the timescale 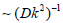 typical for standard diffusion. The frequencies ωI
and ωH
describe oscillations of the impurities caused by the combined
action of electric current and the Hall effect. The considered waves
are oscillatory if | ωI + ωH|> ωR. The latter condition is equivalent to
typical for standard diffusion. The frequencies ωI
and ωH
describe oscillations of the impurities caused by the combined
action of electric current and the Hall effect. The considered waves
are oscillatory if | ωI + ωH|> ωR. The latter condition is equivalent to
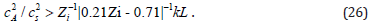
Therefore, the waves are oscillatory if the magnetic pressure is substantially greater than the gas pressure. The frequency of diffusion waves is higher in the region where the magnetic field has strong gradients. The order of estimate of ωI is
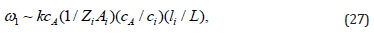
Where li = ciτi Note that different impurities in such waves oscillate with different frequencies.
Conclusion
Diffusion of heavy ions in plasma under the influence of the current-driven mechanism has a number of features. Generally, the diffusion velocity can be comparable to (or even greater than) that caused by other diffusion mechanisms. The currentdriven mechanism can lead to a formation of chemical spot even if the magnetic field is relatively weak. Note that other diffusion mechanisms usually require a much stronger magnetic field. The current-driven 83 diffusion is caused by the Hall effect and electric current and, therefore, it leads to diffusion of heavy ions in the direction perpendicular to both the magnetic field and current. Therefore, a distribution of elements is determined by a geometry of the magnetic fields and electric currents. Chemical inhomogeneities can manifest themself, for instance, by a nonuniform distribution of plasma temperature and emission. Note that this type of diffusion can be important also in some conductive fluids if the magnetic field is sufficiently strong. Our consideration shows that a special type of magnetohydrodynamic waves may exist in multicomponent plasma.
These waves can be periodic if the magnetic field is
sufficiently strong, and they are characterized by oscillations of
the impurity number density alone. The frequency of such waves
is rather low and is determined by a characteristic diffusion
time. The order of magnitude estimates of this frequency yields 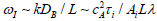 Lλ where λ = 2π / k is the wavelength. In
stellar conditions, such waves can manifest themselves in pecular
magnetic stars where the magnetic field is ∼ 104 G and the number
density and temperature are ∼ 1014 cm−3 and ∼ 104 K, respectively.
If the length scale, L, and λ are of the same order of magnitude (for
instance, ∼ 1011 cm), then the period of such compositional waves
is ∼ 3 × 103 yrs. This is much shorter than the magnetic timescale
and generation of such waves should lead to short-term spectral
variability. Such waves can exist in laboratory plasmas as well, but
their frequency is much higher in this case. If B ∼ 105 G, n ∼ 1015
cm−3, T ∼ 106K, and L ∼ l ∼ 102 cm, then the period of compositional
waves is ∼ 10−8 s. Note that frequencies of waves with various
impurities can differ essentially since they depend on the sort of
heavy ions.
Lλ where λ = 2π / k is the wavelength. In
stellar conditions, such waves can manifest themselves in pecular
magnetic stars where the magnetic field is ∼ 104 G and the number
density and temperature are ∼ 1014 cm−3 and ∼ 104 K, respectively.
If the length scale, L, and λ are of the same order of magnitude (for
instance, ∼ 1011 cm), then the period of such compositional waves
is ∼ 3 × 103 yrs. This is much shorter than the magnetic timescale
and generation of such waves should lead to short-term spectral
variability. Such waves can exist in laboratory plasmas as well, but
their frequency is much higher in this case. If B ∼ 105 G, n ∼ 1015
cm−3, T ∼ 106K, and L ∼ l ∼ 102 cm, then the period of compositional
waves is ∼ 10−8 s. Note that frequencies of waves with various
impurities can differ essentially since they depend on the sort of
heavy ions.
In terrestrial conditions, the compositional waves also can manifest themselves by oscillations in spectra. In astrophysical conditions, the magnetic field has usually more complex topology than that considered in our model. In some cases, however, cylindrical magnetic configurations can mimic the magnetic field in certain regions. For example, the field near the magnetic poles in stars has approximately cylindrical symmetry [13] and our results describe qualitatively diffusion in the region near the poles. Therefore, the current-driven mechanism in combination with other diffusion processes contributes to a formation of chemical spots in various types of stars. For example, this mechanism can contribute to formation of element spots in Ap-stars where the magnetic fields have been detected. Also, many neutron stars have strong magnetic fields and topology of these fields is rather complex with spot-like structures at the surface. Such magnetic configurations can be responsible for formation of a spot-like chemical distribution at the surface. For example, evolution of neutron stars is very complicated, particularly, in binary systems [14] and, therefore, their surface chemistry can be complicated as well. Diffusion processes may play an important role in this chemistry.
Conflicts of Interest
The author declare no conflict of interest.
References
- Vekshtein G (1987) Thermomagnetic effects in rarefied plasma. In Review of Plasma Physics: Ed. B.Kadomtzev; NY:120 Consultants Bureau, USA 15: 1-76.
- Ren Y, Yamada M, Ji H, Gerhardt S, Kulsrud R (2008) Identification of the Electron-Diffusion Region during Magnetic Reconnection in a Laboratory Plasma. Phys Rev L 101: 5003-5006;
- Kagan G, Tang XZ (2012) Electro-diffusion in a plasma with two ion species. Phys Plasma 19: 2709.
- Losseva T, Popel S, Yu MY, Ma JX (2008) Ambipolar diffusion in complex plasma. Phys Rev 75(127): 6403-6407.
- Molvig K, Vold E, Dodd E, Wilks S (2014) Nonlinear Structure of the Diffusing Gas-Metal Interface in a Thermonuclear Plasma. Phys Rev L 113: 9904-9907.
- Ott T, Bonitz M (2011) Diffusion in a Strongly Coupled Magnetized Plasma. Phys Rev L 107: 50030-50030.
- Braginskii S (1965) Transport Processes in a Plasma. Reviews of Plasma Physics 1: 205-363.
- Spitzer L (1978) Physical Processes in the Interstellar Medium, Wiley: New York.
- Tayler RJ (1973) The adiabatic stability of stars containing magnetic fields-I. Toroidal fields. Mon Not R Astr Soc 61: 365-377.
- Bonanno A, Urpin V (2011) Resonance instability of axially symmetric magnetostatic equilibria. Phys Rev E 84: 6310.
- Bonanno A, Urpin V (2011) The magnetohydrodynamic instability uf current-carrying jets. Astron Astrophys 525A: 100.
- Urpin V (1981) Transport phenomena and abundance anomalies in cosmic plasma. Astrophys Sp Sci 79: 11.
- Urpin V, ChanmugamG, Sang Y (1994) Long-term evolution of crustal neutron star magnetic fields. Astrophys J 433: 780-785.
- Urpin V, Konenkov D, Geppert U (1998) Evolution of neutron stars in high-mass X-ray binaries. Mon Not R Astr Soc 299: 73-77.

 Review Article
Review Article