Abstract
Based on the real-time dynamic data of the epidemic situation of COVID-19 published on the website of Ding xiang yuan and the current tracing data of the number of people infected with COVID-19 in academic circles, this paper takes Beijing, Shanghai, Guangzhou, Shenzhen, Chongqing and Wuhan as the research objects. Based on the susceptible-exposed-infected-removed (SEIR) compartment model and the assumption that the infection cases with symptoms occurred before January 26, 2020 were resulted from free propagation without intervention, we calculated the basic regeneration number R0 of COVID-19 and the dynamic change of effective regeneration number Rt from January 25, 2020 to February 22, 2020 (the end of the first month of the lunar calendar). Based on the travel intensity data of the six cities in 2019 and 2020, the effective regeneration number Rt0 under the normal travel intensity in the same period last year is calculated.
Introduction
The novel coronavirus infection has been spreading around the world since the beginning of 2020. The critical parameters of covid-19 epidemic dynamics are of great significance to evaluate the ability of disease transmission and predict the trend of transmission. It can provide important data support for the formulation of corresponding intervention and prevention measures.The basic reproduction number R0refers to the average number of an infected person who can infect before recovery in a group composed of all susceptible individuals. In epidemiology, R0>1 means that the disease will break out, and R0<1 means that the disease is going to die out. Therefore, R0 is an important condition for judging whether an epidemic will break out [1].However, in the transmission process of the real epidemic, the implementation of government intervention policy will change individual behavior, such as wearing masks, reducing travel and so on. The reduction of the number of susceptible populations makes it difficult to satisfy the ideal model conditions defined by the basic reproduction number. In order to describe the evolution process of epidemic over time, we define the average number of infected individuals in an infected state at a certain time (t) in the transmission process as the effective reproduction number, which is recorded as R0t. In the process of actual epidemic control, when R0t<1, means the average number of infected individuals is less than 1, it is considered that the disease has been controlled and the disease will die out[2].
Methods
The Establishment of Free Propagation Period without Intervention
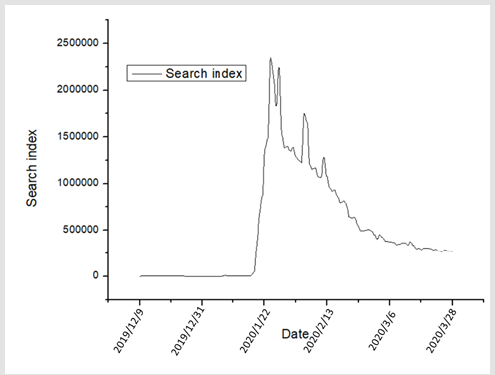
The coverage of COVID-19 communication in China’s mainstream media began on January 21, 2020. At 22:40 am on February 2, 2020, Hubei provincial government launched a public health emergency response. According to the Baidu search index of “novel coronavirus” in Chinese (Figure 1), the awareness and concern of Chinese netizens towards COVID-19 began in late January 2020. Therefore, it can be approximately considered that almost all cases diagnosed on or before January 25, 2020 were caused by free infection without effective intervention and prevention and control measures [3]. Before January 25, the spread of COVID-19 is in the period of free transmission without intervention [4]. The general public lack of cognitive channels and publicity of COVID-19, and the general public has not made relevant behavioral changes to respond to the epidemic prevention and control. However, the cases confirmed after January 25, 2020 (Wuhan locked down) no longer met the definition of non-intervention free transmission.
Establishment of SEIR Model
The early free propagation of COVID-19 is described by a SEIR model including “susceptible-exposed-infected-removed” individuals [5]. Suppose that an infected individual (I) is in contact with a susceptible individual (S), and the probability (infection rate) of the susceptible individual to be infected into the incubation period (infection rate) is β; An exposed individual (E) in the incubation period will be infected with the probability of is transformed into I state; an individual of I state will be transformed into I state in unit time with probability changes to R state (unit time is days). The SEIR model can be described by the following differential equations:
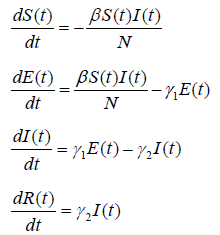
Where N is the total number of individuals in the system, and N = s(T) + e(T) + I(T) + R(T).
Formula of Basic Reproduction Number
Therefore, when t tends towards zero, S(T) approaches N, and the basic reproduction number R0can be expressed as:
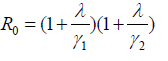
Where 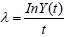 is the growth rate of the early exponential
growth, Y(t) is the number of symptomatic infections up to time
t. The incubation period and infection period can be expressed as
is the growth rate of the early exponential
growth, Y(t) is the number of symptomatic infections up to time
t. The incubation period and infection period can be expressed as 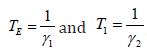 , respectively. The generation time can be
approximately the sequence interval, that is,
, respectively. The generation time can be
approximately the sequence interval, that is, 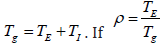 is the ratio of incubation period to generation time, the basic
regeneration number can be expressed as follows:
is the ratio of incubation period to generation time, the basic
regeneration number can be expressed as follows:
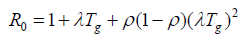
Formula of Effective Reproduction Number
In contrast to R0 the effective reproductive number measures the number of secondary cases generated by an infectious case once an epidemic is underway. In the absence of control measures, Rtsub>=R0X [7], where 𝑥∈ (0,1) is the proportion of the population susceptible. During an epidemic, declines because of the depletion of susceptible in the population and the implementation of specific control measures. To stop an outbreak, Rt must be maintained below 1. According to the relevant paper [7], is calculated as follows:
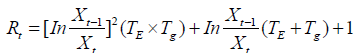
Where TE is the average latent period, Tg the average latent infectious period, the logarithmic growth rate of the case counts as reported by China CDC. We set TE=7 days and Tg =10 days, therefore, TI=3 days [8].
Results
Calculation Results of Basic Reproduction Number
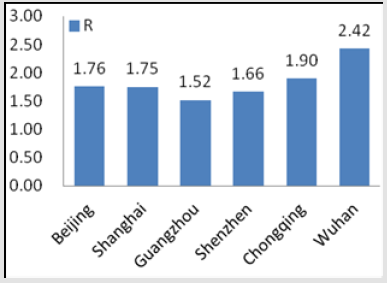
First case of COVID-19 was diagnosed in December 1, 2019 [8] according to the relevant research, so we set t=56. As of January 25, 2020, COVID-19 cases in Beijing, Shanghai, Guangzhou, Shenzhen, Chongqing and Wuhan were 41, 40, 14, 27, 75 and 618 respectively. Therefore, the basic regeneration number of each city can be calculated, and the calculation results are shown in the Figure 2. The Figure 3 shows the R0 of COVID-19 in Wuhan is about 2.42, which is significantly higher than that in other cities.
Calculation Results of Effective Reproduction Number
It can be seen from the relevant research [9-11] that:
Rt = Kt ×bt×TgAmong them, Ktis the number of contacts between the infected and the susceptible at time t, b represent the probability of success of each contact, and Tg is the average duration of the infection period. It is assumed that there is no travel restriction policy within the city after the appearance of COVID-19. If other protective measures remain unchanged, citizens will still travel in the same period last year, then the contact times between the infected and susceptible persons at time t should be expressed as Kt0 and the effective regeneration number should be Rt0.Among them, TI2019means travel intensity in cities this year; TI2020means travel intensity in cities this year.
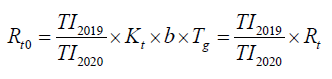
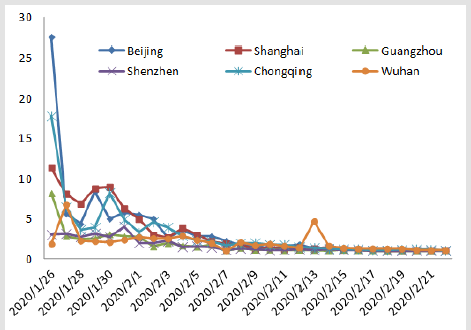
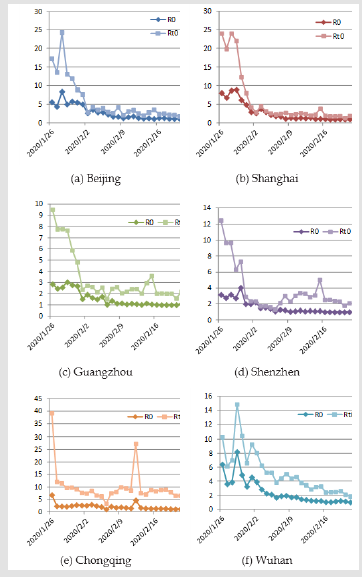
It can be seen from the Figure 4 that after the appearance of COVID-19, if the citizens of Beijing, Shanghai, Guangzhou, Shenzhen, Chongqing and Wuhan still travel with the normal travel intensity of the same period last year, the effective regeneration number Rt0will be significantly greater than the actual effective regeneration number Rt. The travel restriction policy within the city has played a key role in the prevention and control of the epidemic.
This work was supported in part by the Educational Reform Project of Beijing Information Science and Technology University under Grant number 5112010826, Research Base Project of the Social Science Foundation of Beijing under Grant number 19JDGLB2019, and Special Project for Improving Public Service Capacity in the Field of Industry and Information technology under Grant No. 2019-00909-2-1.
References
- Adnerson RM, May RM(1991) Infectious Diseases of Humans: Dynamics and Control. Oxford University Press, Oxford.
- Duan-bing Chen, Wei Bai, Yan Wang, Min Wang, Ping Yu, et al. (2020)Quantitative Evaluation on the Prevention and Control Efficacy of COVID-19.Journal of University of Electronic Science and Technology of China 49(03):339-344.
- Pastor-Satorras R, Castellano C, Mieghem PV (2015) Epidemic processes in complex networks. Review of Modern Physis 87(3): 925-979.
- Zhou Tao, Liu Quanhui, Yang Zimo, Liao Jingyi, Yang Kexin, et al. (2020) Preliminary prediction of the basic reproduction number of the novel coronavirus 2019-nCoV. Chinese Journal of Evidence-Based Medicine 13(1): 359-364.
- Lipsitch M, Cohen T, Cooper B, James M, Stefan M, et al. (2003) Transmission dynamics and control of severe acute respiratory syndrome. Science 300(5627): 1966-1970.
- Li Qun, Guan Xuhua, Wu Peng, Wang X, Lei Z, et al. (2020)Early Transmission Dynamics in Wuhan, China,of Novel Coronavirus-Infected Pneumonia.N Engl J Med 382:1199-1207.
- Yang Zifeng, Zeng Zhiqi, Wang Ke, Soon SW, Wenhua L, et al. (2020)Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. Journal of Thoracic Disease 12(3):165-174.
- Prem Kiesha, Liu Yang, Russell Tim,Adam J, RM Eggo, et al. (2020)The effect of control strategies that reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China. MedRxiv5(5): E261-E270.
- Chaolin Huang, Yeming Wang, Xingwang Li, Lili Ren, Jian PZ, et al. (2020) Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. The Lancet Journal 395(10223): 497-506.
- Zhidong Cao, Qingpeng Zhang, Xin Lu, Dirk Pfeiffer, Zhongwei Jia, et al. (2020)Estimating the effective reproduction number of the 2019-nCoV in China. medRxiv, preprint.
- Wallinga J, Lipsitch M (2007) How generation intervals shape the relationship between growth rates and reproductive numbers. Proceedings of the Royal Society B: Biological Sciences 274(1609): 599-604.

 Research Article
Research Article