Short Communication
Abstract
Application of CBM to the testing of the intersection of a sub-set of basic hypotheses against an alternative one is considered. Optimal decision rule allows us to restrict the Type-I and Type-II errors rates on the desired levels.
Keywords: Intersection-Union Hypotheses; Constrained Bayesian Method; Type-I and Type-II Error Rates
Introduction
In many applications, there arise the problems when basic or/and alternative hypotheses can be represented as the union or intersection of several sub-hypotheses Sen Gupta [1], Roy [2]. The general methodology of testing union-intersection hypotheses was offered in Roy [2]. An idea of this methodology consists in consideration in pairs of sub-hypotheses from basic and alternative hypotheses. Each pair of hypotheses is chosen one by one from basic and alternative hypotheses sub-sets accordingly. Final regions, for acceptance of basic and alternative hypotheses, are defined as intersection of the appropriate sub-regions. The reverse scenario, when basic and/or alternative hypotheses are presented as intersection of the appropriate sub-sets of hypotheses, is considered in Sen Gupta [1]. The special methodology, giving the powerful decision rule, based on Pivotal Parametric Product (P3), is offered there. Application of constrained Bayesian method (CBM), developed by author Kachiashvili [3], to the considered type of hypotheses in one concrete case, is offered below. Here is shown that obtained decision rule allows us to restrict the Type-I and Type-II error rates on the desired level, in this case.
Statement and Solution of the Problem
Let a random variable X follow the distribution f (x;θ ), where θ is scalar parameter. Let’s consider testing
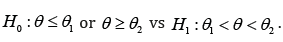(1)Hypothesis H0 can be represented as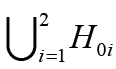 
, where the subhypotheses H01 and H02 are given by H01: θ ≤ θ1 and H02: θ ≥ θ2 That means, we have to test basic hypothesis 
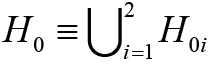against
alternative one H1 when the condition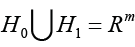 
is fulfilled.
Let’s use one of possible statements of CBM, concretely Task 2 (Kachiashvili, 2018), for solving this problem. Then problem has the following form:
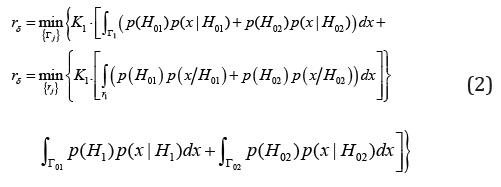
subject to
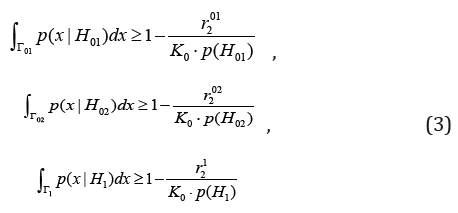
Here p(Hi), p( x| Hi ), i∈Ψ , Ψ ≡ {01,02,1} are a priory probability and the marginal density of x given Hi, Γi is hypothesis Hi acceptance region, ri2 are the restriction levels, K0 and K1 are the losses for incorrectly rejection and incorrectly accepting of hypotheses, respectively.
The solution of the problem (2) and (3) by Lagrange method gives
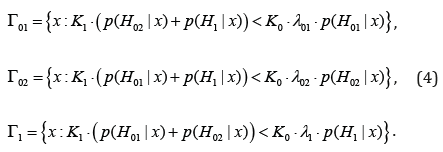
where Lagrange multipliers λ01, λ01 and λ01 are determined so that in the conditions (3) equalities take place.
The errors of the Type-I and the Type-II, accordingly, are:
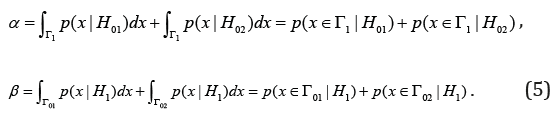
Theorem 1. Testing hypotheses (1), using CBM 2 with restriction levels of (3) ensures a decision rule (4) with the error rates of the Type-I and Type-II, restricted by the following inequalities
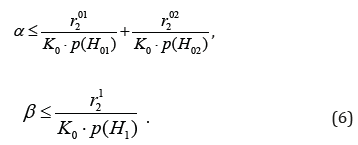
Proof. In contradistinction to the classical case, the following condition is fulfilled in CBM (Kachiashvili, 2018)
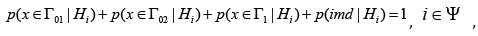
Then the Type-I error rate can be rewritten as follows
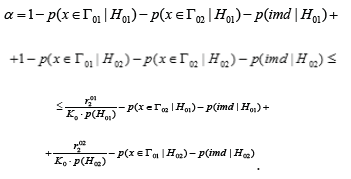
The correctness of the first inequality of (6) is obvious from here.
Similarly, for the Type-II error, we have
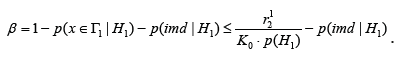
And the correctness of the second inequality of (18) is obvious from here.
Conclusion
Application of CBM to one concrete example of intersectionunion hypotheses testing is considered in the paper. Here is proved that, obtained decision rule guaranty the Type-I and Type-II error rates restricted on the desired levels.
References
- Sen Gupta A (2007) P3 Approach to Intersection-Union Testing of Hypotheses. Invited paper prepared for the SN Roy centenary volume of Journal of Statistical Planning and Inference 137(11): 3753-3766.
- Roy SN (1953) On a heuristic method of test construction and its use in multivariate analysis. Annals of Mathematical Statistics 24: 220-238.
- Kachiashvili KJ (2018) Constrained Bayesian Methods of Hypotheses Testing: A New Philosophy of Hypotheses Testing in Parallel and Sequential Experiments. Nova Science Publishers Inc., New York, USA.
