Association Analysis of Scoliosis Based on Backpack Carrying Methods and Head Positions of Elementary School Students Volume 13 - Issue 5

Wei - Hsiu Hsu¹, Li - Ju Lai², Yo - Ping Huang*^3,4 and Avichandra Singh³

• ¹Department of Orthopedic Surgery, Chang Gung Memorial Hospital, Chiayi, Taiwan 61363
• ²Department of Ophthalmology, Chang Gung Memorial Hospital, Chiayi, Taiwan 61363
• ³Department of Electrical Engineering, National Taipei University of Technology, Taipei, Taiwan 10608
• ⁴Department of Computer Science and Information Engineering, National Taipei University, New Taipei City, Taiwan 23741

Received: January 18, 2019;   Published: January 29, 2019

*Corresponding author: Yo-Ping Huang, Department of Electrical Engineering, National Taipei University of Technology, Taipei, Taiwan 10608

DOI: 10.26717/BJSTR.2019.13.002456

Abstract PDF

To prevent scoliosis development at early stage of growth in elementary school students, we assessed how body posture-namely the school bag carrying method and head position-can affect the morphology of the spinal column. We applied various data mining techniques and multicriteria decision-making to compare the important attributes of scoliosis, in addition to using entropy and principal component analysis to identify the relationship between scoliosis and the various examined attributes. Decision trees were constructed to classify the scoliosis condition of students based on their school bag carrying method, visual acuity, and head position. Association rules were then discovered to represent the associations among different attributes in the database. In this paper, we present several findings, including that the apex of the scoliosis curve in elementary school students is highly dependent on the side on which they carry their backpack, head position, ocular height, and pupil distance. Our analysis results indicate that scoliosis also affects students’ visions. The findings of this study provide a new perspective on the treatment of scoliosis in elementary school students at an early stage and preventing the condition from worsening later on in their development.

Keywords: Scoliosis; Left and Right Tilt; Head Position; Data Mining; Association Rules

Abbreviations: DP: Dorsal Pain; LBP: Low Back Pain; PCA: Principal Component Analysis; MCDM: Multicriteria Decision Making; AHP: Analytical Hierarchy Process; CR: Consistency Ratio; CI: Consistency Index; RI: Random Index

Scoliosis is defined as the lateral curvature of the spine that occurs most often during the growth spurt immediately prior to juvenility. Scoliosis, a segment of the spine being curved sideways, is a common condition that affects many children and adolescents. Idiopathic scoliosis occurs in both genders. The condition progressively worsens during the growth spurt. At the age of 16 years, some juveniles exhibit spinal curvature exceeding 40°. Although scoliosis can be caused by conditions such as cerebral palsy and muscular dystrophy, the causes of most scoliosis cases are unknown. When a person with scoliosis is viewed from the Xray, the spine appears to be curved. Severe scoliosis can be disabling because the severe spinal curve can reduce the amount of space within the chest, hindering proper lung function and causing back pain. One shoulder being higher than the other displaces the head from being centered over the pelvis. Scoliosis is diagnosed through physical examination of the back. If scoliosis is present, the physician then obtains measurements using radiographs and provides a numerical value in degrees. Children can be screened at any age, although idiopathic scoliosis is more commonly discovered during the growth spurt.

Few studies have assessed the association between scoliosis and the backpack carrying methods or head positions of school children. A previous study revealed that older age, walking to and from school, and the backpack carrying method showed statistically significant associations with the severity of back pain [1]. Korovessis et al. investigated the correlation of backpack carrying method, spinal curvature, and athletic activities with dorsal pain (DP) and low back pain (LBP) in 3,441 schoolchildren [2]. Their findings indicate a differential DP and LBP prevalence in schoolchildren and adolescents carrying backpacks in terms of gender and age Moore et al. studied the association of relative backpack weight with back pain in 531 students from 5th to 12th grades in Northern California and found that carrying heavier backpacks is associated with upper and mid-back pain but not neck or lower back pain [3]. Haselgrove et al. reported that neck pain is as common as back pain among adolescents. Weight of the backpack, duration of carrying, and transportation to and from school are associated with back and neck pain [4]. The asymmetric carrying of backpacks results in the shifting of the upper trunk and shoulder and causes cervical lordosis, which may increase back pain overtime [5].

Carrying backpacks on weekdays causes discomfort for schoolchildren, constituting an indirect relationship between backpack load and back pain [6]. Bauer et al. applied electromyography, posture and heart rate evaluation, and ratings of perceived exertion and perceived pain to determine an acceptable backpack load limit for middle school students. They reported that the Borg-CR10 ratings and the trunk flexion angle for the walking trial indicated a possible load limit of 10% body mass [7]. Carrying a school bag on one shoulder has long been considered to be related to LBP and scoliosis, but only limited direct evidence has been presented to explain this phenomenon [7-12]. The parents of children with scoliosis have complained about the “wait and see” approach that many doctors use to evaluate children with scoliosis curves between 10° and 25° [13]. The current medical literature presents no evidence that physical therapy, electrical stimulation, chiropractic care, or other treatment options have any impact on scoliosis curves. The early detection of scoliosis and the application of the correct initial treatment are essential in effective care; therefore, physiotherapists should be aware of the basic criteria for diagnosis and the indications for treatment [14]. Curves in children who are almost full-grown may cease worsening if the correct treatment is applied. Scoliosis can be effectively controlled if the condition can be treated at an early stage [15]. In this study, we investigated the examined data to determine the main causes of scoliosis in young school children. We applied various methods to assess attributes such as the backpack carrying method, head position, and ocular conditions, which may cause scoliosis in elementary school students. The structure of the paper is as follows: Section 2 details problem statement and previous work. Results are presented in section 3. Section 4 discusses the interpretation of our results. The final section concludes our research.

Study Participants

From September 2013 to May 2014, 1,535 participants aged 6-12 years were enrolled from elementary schools in Chiayi County, Taiwan. Written informed consent was obtained from all parents or guardians. This study was approved by the Institutional Review Board of the Chang Gung Foundation (IRB-102-4827B). The research was conducted according to the principles of the Declaration of Helsinki. In addition to obtaining a detailed personal history, general pediatric health examination, ophthalmological assessment, and lifestyle questionnaire were conducted for all participants [16]. Our data showed that most students with scoliosis were girls (Table 1). For comparison, (Table 2) provides the details of the 1,500 students with scoliometer readings of ≤5°. The examined data are presented in the numerical format or in terms of linguistic terms that were grouped into subcategories to obtain association rules among attributes. The data were transformed as follows: head positions were categorized as left tilt, right tilt, and normal. The backpack carrying method was categorized as left side, right side, backpack, and trolley. Ocular heights were represented by left higher, right higher, and identical. For vision, values ranging from 0.1 to 2 were decomposed into three subsets: >1 for visual acuity (VA) > 20/20, = 1 for VA = 20/20, and < 1 for VA < 20/20. Pupil distances ranging from 1 to 77 mm were divided into the high distance for >56 mm, normal for between 41 and 56 mm, and low distance for <41 mm. (Tables 3 & 4) show the mean and standard deviation (SD) values of students with scoliometer readings of >5° and ≤5°, respectively [17-20]. We found that students with scoliometer readings of > 5° had different vision in both left and right eyes. By contrast, students with scoliometer readings of ≤5° did not exhibit vision differences in both eyes. This indicates that the higher scoliometer readings have direct impact on vision. Based on the number of students with scoliometer readings of >5°, 62.86% of girls had a higher risk of scoliosis than boys (37.14%).

Table 1: Details of 35 students with scoliometer readings of >5°.

Table 2: Details of 1,500 students with scoliometer readings of ≤5°.

Table 3: Vision details of 35 students with scoliometer readings of >5°.

Table 4: Vision details of 1,500 students with scoliometer readings of ≤5°.

Measures

Principal Component Analysis: Principal component analysis (PCA) was applied to reduce the number of candidate attributes examined in elementary school students without sacrificing the principal components in the original data set [20-23]. A covariance matrix was created to associate the changes in one attribute with changes in others [24]. A positive entry in the matrix implies that it has a positive correlation with the corresponding attribute. By contrast, a negative entry indicates that it has a negative correlation with the other attribute.

Information Gain: Information gain is one of the most common measures used in data mining to assess attributes’ importance [25]. It represents the expected amount of information for each attribute. The results from the calculation of information gain are used to determine their importance in constructing compact decision trees when numerous candidate attributes are available.

Multicriteria Decision-Making: Selecting the relevant attribute is a fundamental issue that substantially contributes to decision-making, particularly for medical purposes [25-32] In this study, the selection of attributes in multicriteria decision-making (MCDM) included multiple criteria: left and right tilt, normal, high distance, double, trolley, VA < 20/20, VA > 20/20, and VA = 20/20. Two methods of MCDM-namely the analytical hierarchy process (AHP) and technique of order preference by similarity to ideal solution (TOPSIS)-were used to evaluate the criteria that affect the scoliosis condition of students and determine the scores of various alternative attributes. Saaty proposed the AHP in 1980 as a method of solving socioeconomic decision-making problems, and it has been used to solve a wide range of problems [33]. The method involves deriving ratio scales from pairwise comparisons. The input can be obtained from actual measurement values or from subjective or expert opinions such as satisfaction feelings and judgments. It provides a measure of judgment consistency derived from the principal eigenvalue. It derives priorities among the various criteria and alternatives. Final ratings among decision criteria were used for pairwise comparisons. The basic procedure is as follows:

Step 1. Develop the weights for criteria as follows:

a) Develop a pairwise comparison matrix for each criterion.

b) Normalize the resulting matrix.

c) Average the values in each row to obtain the corresponding rating.

d) Calculate and verify the consistency ratio (CR).

Step 2. Develop the rating of each decision alternative for each criterion.

Step 3. Calculate the weighted average rating for each decision alternative. Select the option with the highest score.

In the TOPSIS, two artificial alternatives are considered. The ideal solution is the solution that has the best level for all attributes considered. The negative ideal solution is the solution that has the worst attribute values. The TOPSIS selects the alternative that is closer to the ideal solution and farther from the negative ideal solution [34-38]. The TOPSIS assumes that we have m attributes (options), such as the backpack carrying method, ocular height, pupil distance, head position, and vision acuity for the left eye, which has higher information gain values with respect to scoliosis. MCDM included various criteria such as left, right, normal, high distance, double, VA < 20/20, VA > 20/20 and VA = 20/20. We entered the numbers of students for each criterion with respect to different attributes.

Step 1. Construct a normalized decision matrix. Step 2. Establish the weighted normalized decision matrix. Step 3. Determine the ideal and negative ideal solutions. Ideal solution:

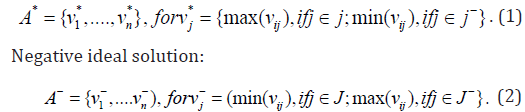
Step 4. Calculate the separation measure for each alternative.

The separation from the ideal solution:

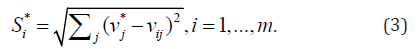
The separation from the negative ideal solution:

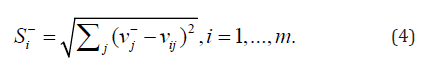
Step 5. Calculate the relative closeness to the ideal solution for different attributes.

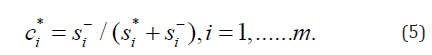
Association Rules: Various data mining techniques have been proposed to identify interesting patterns in large transactional databases [4,6,15,28,30,38-40]. In this study, we applied the Apriori Algorithm data mining technique to extract association rules among attributes from our vision examination database. Assume X and Y are two frequent itemset. To measure the interestingness of a discovered association rule XÞY, three metrics are considered: support, confidence, and lift [15,30]. Support is defined as the probability that both X and Y symptoms appeared simultaneously in the database. Confidence is used to estimate the probability of Y occurrence under the condition that X has occurred. Lift is a measure of rule interestingness that involves further evaluating support thresholds under the existence of both X and Y. The three metrics, support, confidence and lift, are calculated as follows:

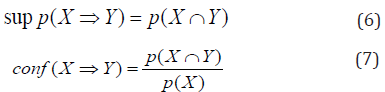
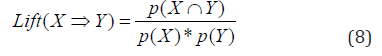
An association rule that overpasses both support and confidence metrics is called an interestingness rule.

Decision Tree: A decision tree is based on given attributes to classify a set of patterns [22,27-28]. The more discriminative attributes were selected to branch the tree earlier, thereby more effectively enabling the construction of a compact decision tree to classify the patterns. The importance of attributes was ranked in descending order according to information gain. An internal node in the tree represents an attribute that uses branches to denote the outcome of the test. A leaf node represents a decision that was made for classification. The paths from the root node to the leaf nodes represent classification rules.

Principal Component Analysis (PCA)

Covariance matrices of seven attributes were selected from the database to support scoliosis. From the covariance matrix, scoliosis was positively correlated with six attributes, except for ocular alignment of –0.139 (Table 5). Therefore, in our analysis, ocular alignment was removed as a variable.

Table 5:Covariance matrix values.

Information Gain

According to the scoliosis examination database, 35 students had scoliometer readings of >5°. Among these 35 students, 85.71% had left tilt scoliosis. We calculated various information gain values for these students and compared them with those of the remaining 1,500 students. Table 6 shows information gain for the attributes positively correlated with scoliosis. The results indicated that for all study subjects, both the backpack carrying method and left vision attributes had a higher correlation with scoliosis than other attributes.

Table 6:Information gain.

Multicriteria Decision-Making (MCDM)

The first step in the AHP is to make a pairwise comparison between the criteria (Saaty, 1980). Saaty and Vargas provided an example scale (Table 7). In the pairwise comparison method, criteria and alternatives are presented in pairs of one or more references [34,38]. It is necessary to evaluate individual alternatives, derive weights for the criteria, construct the overall rating of the alternatives, and identify the best option. Our criteria constitute a 9 × 9 matrix that contains nine criteria. The diagonal elements of the matrix are always 1, and we need only to fill the upper triangular matrix. Table 8 was used to fill the upper triangular matrix. The steps to fill the matrix are provided below:

Table 7: Example scale of comparison (Saaty, 1980).

Table 8:Rules used to fill upper triangular matrix.

Step 1: If the judgment value is on the left-hand side of 1 in Table 8, the actual judgment value was assigned.

Step 2: If the judgment value is on the right-hand side of 1 in Table 8, the reciprocal value was assigned.

Step 3: Fill up the lower triangular matrix by using the reciprocal values of the upper triangle as shown in Table 9.

Step 4: Normalize the matrix by summing the numbers of each column. Each entry in the column is divided by the column sum to yield its normalized score, as shown in Table 10.

he relative weight for each criterion can then be determined by dividing the sum of the normalized column of matrix by the number of criteria 9 to generate a weighted matrix (Table 11) as follows:

Table 9: Full pairwise comparison matrix for different criteria.

Table 10: Normalized pairwise comparison matrix for different criteria

Table 11:Normalized weight for criteria

Calculating and verifying the CR: The purpose of calculating the CR is to ensure that the original preference ratings are consistent. The CR identifies whether comparisons between criteria are subjective judgments [25]. The CR is calculated as the ratio between the Consistency Index (CI) and Random Index (RI), as follows:

where CI is calculated as follows:

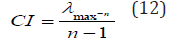
where is obtained from the summation of products between each element of an eigenvector and the sum of columns of the reciprocal matrix as follows:

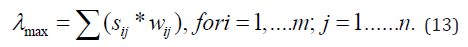
Then, we have lmax = 10.028 and CI = 0.128.

Random Index (RI) Saaty provided RI numbers for different sizes of matrix, as shown in Table 12 [29]. Hence, we can obtain CR = 0.089 or 8.90% for a pairwise comparison under different criteria. If the value is less than or equal to 10%, then the CR is acceptable. By contrast, if the CR is higher than 10%, the subjective judgment needs to be revised. In this study, CR was 8.90%; therefore, our subjective judgment was acceptable.

Table 12:Random index to the order of matrix. Note: n is the order of matrix.

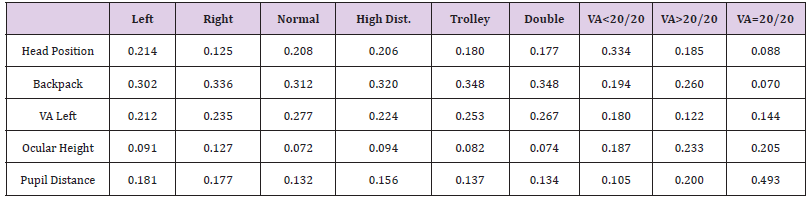
The next step involved verifying the CR for different criteria with respect to different alternatives. Table 13 shows that the ratio was designed in such a way that they were less than 10%. This value indicates a reasonable level of consistency in the pairwise comparison between criteria with respect to different alternatives. Higher CR indicates lack of information or lack of understanding. The rating weight for each decision alternative was obtained through a pairwise comparison between different alternatives with respect to various criteria, as shown in Table 14.

Table 13: Consistency ratio (CR) for different criteria with respect to pairwise comparison for different alternatives.

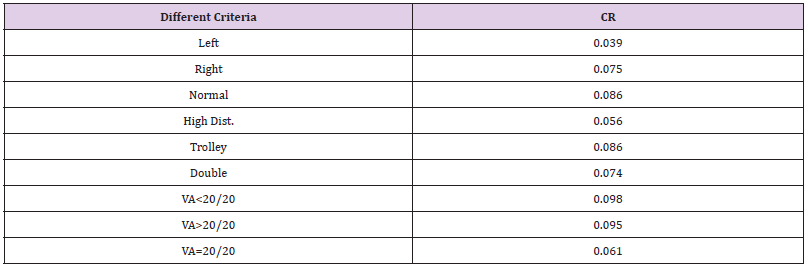
Table 14: Weight for each alternative from pairwise comparison between alternatives with respect to criteria.

The weighted average rating for each decision alternative can be calculated as follows:

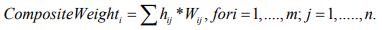
where hij is the weight for a pairwise comparison between different alternatives with respect to various criteria. Wij is the weight for a pairwise comparison between different criteria. Table 15 shows that the backpack carrying method has the highest value, at 29.1% association with scoliosis, followed by VA for left eye with a value of 22.6%. Ocular height, pupil distance, and head position have lower composite weights.

Table 15:Weighted average rating for different alternatives.

Technique of Order Preference by Similarity to Ideal Solution (TOPSIS)

(Table 16) provides the scores of alternatives or the numbers of students from the database, with respect to their attributes. Scores in Table 16 can be further normalized as follows:

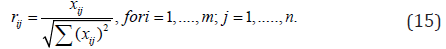
We can then construct the weighted normalized decision matrix as follows:

The assumed weight for each criterion is provided in Table 17. After constructing the weighted normalized decision matrix, the ideal and negative ideal solutions can be determined using Eqs. (1) and (2); the results are shown in Table 18.

Table 16: Scores for different attributes with respect to their criteria.

Table 17: Assumed weight for each criterion.

Table 18:Ideal and negative ideal solutions.

For scoliometer readings of >5°, we selected the ideal and negative ideal solutions according to our assumption. We could then determine the ideal and negative ideal separation values for each alternative by using Eqs. (3) and (4); the values are provided in Table 19. The final step involved calculating the relative closeness to the ideal solution for different attributes by using Eq. (5); the results are shown in Table 20.

Table 19: Ideal and negative ideal separation values.

Table 20: Relative closeness to the ideal solution for different attributes.

Association Rules

Association rules were discovered to represent associations among different items in the transaction databases. In this section, we presented interesting association rules obtained from the attributes, namely backpack carrying method, VA, ocular height, pupil distance, and head position with high information gain values from (Table 6). The backpack carrying method had the components of left side, double, and trolley. The ocular height had the components of left higher, right higher, and identical height. The pupil distance had the components of high and normal distance. The head position had the components of left and right tilt. VA had the components of VA < 20/20, VA > 20/20, and VA = 20/20. The thresholds for support and confidence values were set to 0.05 and 0.5, respectively. A lower support threshold results in many redundant rules that may not be truly interesting. By contrast, a higher threshold filters out interesting rules at the early mining stage. (Tables 21-23) provide some of the interesting rules from thresholds of support = 0.05 and confidence = 0.5. Note that in Tables 21-23, Li represents the large i-itemset.

Table 21:L3 association rules.

Table 22: L4 association rules.

Table 23: L5 association rules.

Decision Tree

A decision tree was constructed to facilitate rapid judgement of whether a new subject has right or left scoliosis. Because the backpack carrying method had the highest information gain of 0.59, it was selected as the top priority for constructing the decision tree. The branching of the tree continues until a decisive leaf node is reached or until all the attributes are used up. Figure 1 shows a decision tree constructed for judging if a student has right or left scoliosis.

Figure 1:Different cognitive examinations.

Association Analysis

This study assessed the association of scoliosis with the backpack carrying method, head position, and ocular condition in young school children. Of 1,535 students, 35 students with scoliometer readings larger than 5° were studied. This study found that girls had worse scoliosis than boys, consistent with the findings of previous studies. As a child grows, the development of the musculoskeletal system occurs through different phases. In particular, the skeletal stature and height exhibit a constant increase from the age of 5 years. During this period, regularly carrying heavy backpacks either on the left or right shoulder to, from, and at school results in spinal curvature. Numerous previous studies have reported that carrying heavy backpacks causes back pain. To the best of our knowledge, previous studies have been based on data collected from clinics or hospitals. Furthermore, only a few studies have been conducted on elementary school children [7]. Our data set was collected by our coauthor (Dr. Lai), who has long-term experience as a volunteer setting up temporary clinics to examine students’ vision before examining school children in each elementary school. Scoliosis starts to develop at an early age, and its severity continues to adolescence. The backpack carrying method used by students depends on their preferences and their lack of awareness of the consequences. Backpacks should preferably be carried over both shoulders to distribute the weight equally on the spine and shoulders. However, students tend to choose the backpack carrying method based on fashion criteria rather than ergonomic characteristics. Carrying heavy backpacks over one shoulder during early childhood generates a high torque around the spine, which may cause scoliosis.

To identify the most important attributes among the considered attributes, we compared two multicriteria decision-making processes, namely the AHP and TOPSIS. The results of both methods indicated that the backpack carrying method had the highest composite weight. After comparing the results obtained through other methods, we found that the tilt side was highly related to the method used students to carry their backpack, head position, pupil distance, and ocular height. Students’ vision was also affected by scoliosis. If students with a high pupil distance carry their backpack on their left side, with their head position tilted to the right side, and have left tilt scoliosis, then their chance of having worsened vision has a support value of 0.34, confidence value of 0.71, and lift value of 1.12. Table 6 indicates that the backpack carrying method and vision are the top two attributes with higher information gain for students possessing scoliometer readings of >5°.

Our association analysis revealed that if students carry backpacks on their left shoulder, then their scoliosis is tilted to the left, and their head positions are tilted to the right. By contrast, if students carry their backpacks on their right shoulder, then their scoliosis is tilted to the right, and their head positions are tilted to the left. This finding indicates that students carrying backpacks on one shoulder need to compensate for the bag weight by tilting their head position to the opposite side. If the practice of carrying a backpack on one shoulder to, from, and at school occurs for a long period, then it causes scoliosis in young school children.

Strengths and Limitations of the Study

Various factors affect scoliosis in elementary school students. In this study, initially, the PCA method was applied to select important and correlated attributes of scoliosis. Information gain was then used to recognize how many attributes were correlated with scoliosis. The AHP and TOPSIS methods of MCDM were applied to identify which attributes had high scores with respect to scoliosis. A decision tree was constructed by using the ranked attributes to classify the training subjects’ patterns. An effective decision tree could later be used to classify new subjects’ scoliosis tilt side and conditions. Furthermore, by scanning the database, we could discover many interesting association rules that relate one or more attributes to others. Numerous notable results were revealed in this study. For example, if students carry their backpack on their left shoulder and have a high pupil distance and a right-tilted head position, then they have a chance of left tilt scoliosis with a support value of 0.49, confidence value of 1.00, and lift value of 1.17. This study is limited to analysis of abnormal scoliometer degrees. Of 1,535 students, 35 had tilt scoliosis higher than 5°. The results of this study were confined to the limited information available in examined records showing only that tilt scoliosis was either larger than or smaller than 5°, rather than the exact figures. Future studies should develop a method that can automatically weigh backpacks and record the time for which the bag is carried each day.

Juvenile idiopathic scoliosis was found in children aged 6-12 years and continued to cause curvature of the spinal column up to 30-40° at the stage of adolescence if the children did not take proper medication and undergo proper treatment. Prevention is better than cure; therefore, in our research, we applied various methods to identify the main causes of scoliosis for students who developed scoliosis at a young age to prevent their scoliosis from further worsening at the stage of adolescence. Our analytical results indicated that scoliosis was substantially affected by the backpack carrying method, head position, pupil distance, and ocular height. Furthermore, our data indicated that girl students were more susceptible to scoliosis than boys. Scoliosis was also associated with the vision of elementary school students. Without proper intervention or medication, scoliosis may become worse. It would be interesting to follow-up the students evaluated in the present study to observe for any improvement of scoliometer degrees after 2-3 years of medication use. Further research can provide more evidence to compare with current results because adolescent idiopathic scoliosis is age-related.

This study was funded in part by the Ministry of Science and Technology, Taiwan, under Grants MOST107-2221-E-027-113- and by a joint project between the National Taipei University of Technology and the Chang Gung Memorial Hospital under Grant NTUT-CGMH-106-05, and in part by the Chang Gang Memorial Hospital under grant CMRPG6G0121.

1. Bauer DH, Freivalds A (2009) Backpack load limit recommendation for middle school students based on physiological and psychophysical measurements. Work 32(3): 339-350.
2. Berdishevsky H, Lebel VA, Bettany Saltikov J, Rigo M, Lebel A, et al. (2016) Physiotherapy scoliosis-specific exercises - a comprehensive review of seven major schools. Scoliosis and Spinal Disorders 11(20).
3. Black DAJ, Pilcher C, Drake S, Maude E, Glynn D (2017) Current knowledge of scoliosis in physiotherapy students trained in the United Kingdom. Scoliosis and Spinal Disorders 12(34).
4. Chazard E, Ficheur G, Bernonville S, Luyckx M, Beuscart R (2011) Data mining to generate adverse drug events detection rules IEEE Trans. on Information Technology in Biomedicine 15(6): 823-830.
5. Dianat I, Alipour A, Jafarabadi MA (2017) Prevalence and risk factors of low back pain among school age children in Iran. Health Promotion Perspectives 7(4): 223-229.
6. Fang G, Pandey G, Wang W, Gupta M, Steinbach M, et al. (2012) Mining low-support discriminative patterns from dense and high-dimensional data. IEEE Trans. on Knowledge and Data Engineering 24(2): 279-294.
7. Forjuoh SN, Lane BL, Schuchmann JA (2003) Percentage of body weight carried by students in their school backpacks. American Journal of Physical Medicine & Rehabilitation 82(4): 261-266.
8. Harish KS (2012) A fuzzy logic multi-criteria decision approach for vendor selection manufacturing system. International Journal of Modern Engineering Research 2(6): 4189-4194.
9. Haselgrove C, Straker L, Smith A, O’Sullivan P, Perry M, et al. (2008) Perceived school bag load, duration of carriage, and method of transport to school are associated with spinal pain in adolescents: an observational study. Australian Journal of Physiotherapy 54(3): 193-200.
10. Huang YP, Huang CY, Liu SI (2014) Hybrid intelligent methods for arrhythmia detection and geriatric depression diagnosis. Applied Soft Computing 14(A): 38-46.
11. Korovessis P, Koureas G, Papazisis Z (2004) Correlation between backpack weight and way of carrying, sagittal and frontal spinal curvatures, athletic activity, and dorsal and low back pain in schoolchildren and adolescents. Journal of Spinal Disorders & Techniques 17(1): 30-40.
12. Korovessis P, Koureas G, Zacharatos S, Papazisis Z (2005) Backpacks, back pain, sagittal spinal curves and trunk alignment in adolescents: a logistic and multinomial logistic analysis. Spine 30(2): 247-255.
13. MacDonald J, Stuart E, Rodenberg R (2017) Musculoskeletal low back pain in school-aged children: a review. JAMA Pediatrics 171(3): 280-287.
14. Malathy EM, Muthuswamy V (2015) Knapsack - TOPSIS technique for vertical handover in heterogeneous wireless network. PLOS ONE, 10(8): e0134232.
15. Mallik S, Mukhopadhyay A, Maulik U (2015) RANWAR: rank-based weighted association rule mining from gene expression and methylation data. IEEE Trans. on NanoBioscience 14(1): 59-66.
16. Mehrdad R, Shams Hosseini NS, Aghdaei S, Yousefian M (2016) Prevalence of low back pain in health care workers and comparison with other occupational categories in Iran: a systematic review. Iranian Journal of Medical Sciences 41(6): 467-478.
17. Moore MJ, White GL, Moore DL (2007) Association of relative backpack weight with reported pain, pain sites, medical utilization, and lost school time in children and adolescents. Journal of School Health 77(5): 232- 239
18. Munkholm A, Bjorner JB, Petersen J, Micali N, Olsen EM, et al. (2017) Validation of the eating pattern inventory for children in a general population sample of 11- to 12-year-old children. Assessment 24(6): 810-819.
19. Negrini S, Carabalona R (2002) Backpacks on! schoolchildren’s perceptions of load, associations with back pain and factors determining the load. Spine 27(2): 87-195.
20. Negrini A, Negrini MG, Donzelli S, Romano M, Zaina F, et al. (2015) Scoliosis-specific exercises can reduce the progression of severe curves in adult idiopathic scoliosis: a long-term cohort study. Scoliosis 10(20).
21. Nguyen HT, Dawal SZ, Nukman Y, Aoyama H, Case K (2015) An integrated approach of fuzzy linguistic preference based AHP and fuzzy COPRAS for machine tool evaluation. PLOS ONE 10(9): e0133599.
22. Nguyen MN, Zurada JM, Rajapakse JC (2011) Toward better understanding of protein secondary structure: extracting prediction rules. IEEE/ACM Trans. on Computational Biology and Bioinformatics 8(3): 858-864.
23. Noll M, Silveira EA, Avelar IS (2017) Evaluation of factors associated with severe and frequent back pain in high school athletes. PLOS ONE 12(2): e0171978.
24. Oosterhuis HE, van der Ark LA, Sijtsma K (2016) Sample size requirements for traditional and regression-based norms. Assessment 23(2): 191-202.
25. Parthiban P, Abdul HZ, Chintamani PG (2012) A multi criteria decision making approach for supplier’s selection. International Conference on Modelling Optimization and Computing 38: 2312-2328.
26. Pialasse JP, Descarreaux M, Mercier P, Blouin L, Simoneau M (2015) The vestibular-evoked postural response of adolescents with idiopathic scoliosis is altered. PLOS ONE 10(11): e0143124.
27. Rutkowski L, Jaworski M, Pietruczuk L, Duda P (2014) Decision trees for mining data streams based on the Gaussian approximation. IEEE Trans. on Knowledge and Data Engineering 26(1): 108-119.
28. Rutkowski L, Pietruczuk L, Duda P, Jaworski M (2013) Decision trees for mining data streams based on the Mc Diarmid’s bound. IEEE Trans. on Knowledge and Data Engineering 25(6): 1272-1279.
29. Saaty TL (1980) The analytic hierarchy process, McGraw-Hill, New York.
30. Samarah S, Boukerche A, Habyalimana AS (2011) Target association rules: a new behavioral pattern for point of coverage wireless sensor networks. IEEE Trans. on Computers 60(6): 879-889.
31. Schlösser TP, van der Heijden GJ, Versteeg AL, Castelein RM (2014) How ‘idiopathic’ is adolescent idiopathic scoliosis? a systematic review on associated abnormalities. PLOS ONE 9(5): e97461.
32. Siambanes D, Martinez JW, Butler EW, Haider T (2004) Influence of school backpacks on adolescent back pain. Journal of Pediatric Orthopaedics 24(2): 211-217.
33. Valavanis I, Maglogiannis I, Chatziioannou AA (2015) Exploring robust diagnostic signatures for cutaneous melanoma utilizing genetic and imaging data. IEEE J. of Biomedical and Health Informatics 19(1): 190- 198.
34. Wang Y, Xi C, Zhang S, Zhang W, Yu D (2015) Combined approach for government e-tendering using GA and TOPSIS with intuitionistic fuzzy information. PLOS ONE 10(7): e0130767.
35. Wu MC, Chen TY (2011) The ELECTRE multicriteria analysis approach based on Atanassov’s intuitionistic fuzzy sets. Expert Systems with Applications 38(10): 12318-12327.
36. Xu K, Chandrashekar J, Zhang ZL (2010) Principal component analysis of BGP updates streams. J. of Communications and Networks 12(2): 191- 197.
37. Loglisci C, Malerba D (2017) Leveraging temporal autocorrelation of historical data for improving accuracy in network regression. Statistical Analysis and Data Mining 10(1): 40-53.
38. Yuen KKF (2014) Fuzzy cognitive network process: comparisons with fuzzy analytic hierarchy process in new product development strategy. IEEE Trans. on Fuzzy Systems 22(3): 597-610
39. Purvine E, Cotilla Sanchez E, Halappanavar M, Huang Z, Lin G, et al. (2017) Comparative study of clustering techniques for real-time dynamic model reduction. Statistical Analysis and Data Mining 10(5): 263-276.
40. Zhang G, Wang L, Duffy AP, Febo DD (2015) Applying the analytic hierarchy process (AHP) to an FSV-based comparison of multiple datasets. IEEE Trans. on Electromagnetic Compatibility 57(3): 477-483.