Growth of Phytoplankton Volume 13 - Issue 2

Udriste C* and Tevy I

• Department of Mathematics-Informatics, Faculty of Applied Sciences, Romania

Received: December 21, 2018;   Published: January 16, 2019

*Corresponding author: Udriste C, Department of Mathematics-Informatics, Faculty of Applied Sciences, Splaiul Independentei 313, Bucharest, 060042, Centenary of Romanian Great Union 1818-2018, Romania

DOI: 10.26717/BJSTR.2019.13.002360

Abstract PDF

A central problem in biological dynamical systems is to determine the boundaries of evolution. Although this is a general problem, we prefer to give solutions for growth of the phytoplankton. AMS Mathematical Classiftcation: 92D40, 35B36, 35Q92, 37N25.

Keywords: Phytoplankton Dynamical System; Phytoplankton Sub-strate; Phytoplankton Biomass; Intracellular Nutrient Per Biomasss

Phytoplankton Dynamical System

In the paper of Bernard - Gouze [1] one analyse a model of phytoplankton growth based on the dynamical system

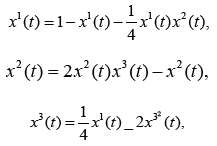
where x¹ means the substrate, x² is the phytoplankton biomass and x³ is the intracellular nutrient per biomass, with the physical domain 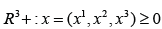The previous dynΣamical system is non cooperative and has the equilibrium point 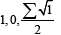We introduce the phytoplankton vector field 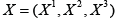of components 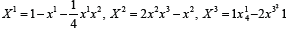and the maximal field line x = x(t, x0), t ∈ I, which satisfies the initial condition x(t0, x0) = x0. In order to find bounds for substrate, biomass, and intracellular nutrient per biomass, we use the techniques of optimization developed in our papers [2-6].

Bounds for Phytoplankton Substrate

We use the following problem: ftnd max f (x1, x2, x3) = x1 with the restriction x=x(t,x₀). We set the critical point condition 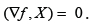. In this case 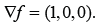It follows the relation 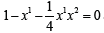The convenient solution (critical point) 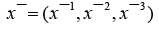must be

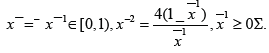
The sufficient condition Hess 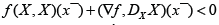reduces to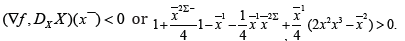

Since at the critical point we have 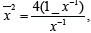the condition goes to 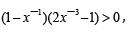and the convenient condition is 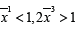. Theorem 2.1. Suppose that on a evolution line (field line) it exists a point x¯ at which we have

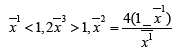
Then the phytoplankton substrate has an upper bound at this point.

Bounds for Phytoplankton Biomass

Let us use the problem: ftnd max 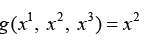subject to x=x(t,x₀).

Growth of phytoplankton: The critical point condition is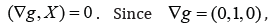 it follows the relation 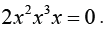The convenient solution (critical point)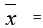 The sufficient condition Hess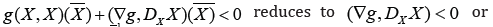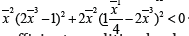Since at the critical point we have , the sufficient condition leads to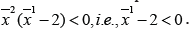

Theorem: Suppose that on a evolution line (field line) it exists a point at which we have

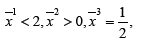
then the x²(t) component of the corresponding field line has an upper bound at this point.

In the direct alternative, we build the composite function g(x(t, x0)). The condition

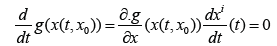
reduces to 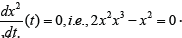the convenient solution is 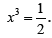The condition 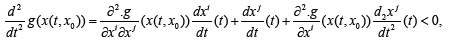becomes 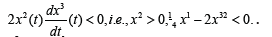Replacing 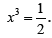we find x² > 0, x¹ − 2 < 0. The same result is obtained as in the previous method.

Now the helping problem is: compute max 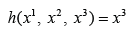with the restriction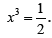

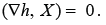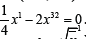The critical point condition is Since Δh = ∇h = (0,0,1), it follows the relation The critical point 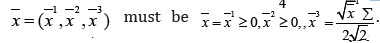The sufficient condition Hess 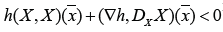reduces to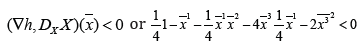

Since at the critical point we have 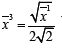the condition goes to

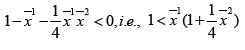
Theorem: Suppose that on a evolution line (field line) it exists a point x at which we have 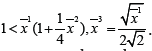Then the intracellular nutrient per biomass has an upper bound at this point.

1. Bernard O, Gouze JL (2002) Global qualitative description of a class of nonlinear dynamical systems. Artificial Intelligence 136(1): 29-59.
2. Calin O, Udriste C (2014) Geometric Modeling in Probability and Statistics, Springer.
3. Udriste C (1994) Convex Functions and Optimization Methods on Rieman-nian Manifolds, Mathematics and Its Aplications 297, Kluwer Aca- demic Publishers.
4. Udriste C (2000) Geometric Dynamics, Mathematics and Its Aplications 513, Kluwer Academic Publishers 24(2): 313-322.
5. Udriste C, Dogaru O (1991) Extrema conditioned by orbits, in Romanian. Sci Bul. IPB 51: 3-9.
6. Udriste C, Dogaru O, Tevy I (2002) Extrema with Nonholonomic Constraints, Geometry Balkan Press.