Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
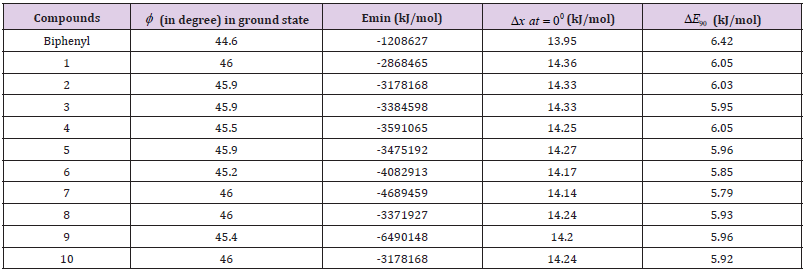
Shu-Hsien Lin1,2, Yu-Fang Shen3,4, Chun-Yu Chiou1, Gialih Lin1 , g. and Gan-Hong Chen*5, g
Received: December 21, 2019; Published: January 09, 2019
*Corresponding author: Gan-Hong Chen, Department of Culinary Art Management, Taiwan Hospitality & Tourism College, Hualien, Taiwan
DOI: 10.26717/BJSTR.2019.13.002332
Rotational barriers of ten 4-acyloxy-4’-N-n-butylcarbamyloxy-biphenyls were calculated by density functional theory. Linear free energy relationships between rotational barriers and reduced mass existed in these compounds. Rotational barriers of these compounds from dihedral angle of 450 to 900 (9E0Δ ’s) were linearly correlated with the inverse of reduced mass (1/m’). Thus, this rotational mechanism was just a simple physical rotation of an object about its center axis. On the other hand, rotational barriers of these compounds from dihedral angle of 450 to 00 ( E0Δ’s)) were dependent upon both 1/m’ and the vibrational energy difference at the C(1)-C(1’) bond near dihedral angle of 00(*σ’s). Values of ()( 1/2vibvibEE=Δ= were linearly correlated with the inverse of the root of reduced mass (1/√m’). Thus, the Δ E0 values calculated from density functional theory combined both physically rotational energy barrier, ΔE90, and vibrational (or stretching) energy barrier, vibEΔ. A two-step mechanism for the rotation of biphenyl from dihedral angle of -450 to 450 through the intermediate with an increasing C(1)-C(1’) pivot bond length of 0.027Ǻ was proposed. Accordingly, values of the bond length incensement of these ten biphenyls were calculated to be from 0.037 to 0.046 Ǻ. Thus, the experimental ΔE0 values were estimated to be the calculated ΔE0 values minus the vibEΔ values.
Keywords: Rotational Barriers; Density Functional Theory; Biphenyls; Gaussian; Linear Free Energy Relationship
One of the paradoxical results in Chemistry was that the rotational barriers of biphenyls obtained from experiments were significant different to those calculated by quantum mechanism. In the gas-phase experiments, Bastiansen and Samdal estimated the barriers from ground state (dihedral angle, φ= 450) to φ= 00 and φ= 90o to be 0 6.02.1E=Δ±kJ/mol and 90 6.52.E0Δ=±kJ/mol, respectively [1]. Theoretical calculation for rotation barriers of biphenyl by different levels of basis sets of quantum mechanism was always active in this field since the second half of last century. Tsuzuki and Tanabe reported E0Δ = 13.93 kJ/mol and 9E0Δ= 6.32 kJ/mol from HF/6-31G** level of quantum mechanism calculation [2]. Rubio et al. found E0Δ= 12.93 kJ/mol and 9E0Δ= 6.40 kJ/mol from 4s3p1d/2s1p basis set level of quantum mechanism calculation [3]. Karpfen et al. estimated that the E0Δvalues were 13.8, 16.3, and 8.4 kJ/mol and that the 9E0Δvalues were 6.3, 7.5, and 10.0 kJ/mol by SCF, MP2, and B3LYP methods, respectively [4].
Values of E0Δwere 13.0 and 8.4 kJ/mol and 9E0Δwere 5.0 and 7.3 kJ/mol using the 6-311++G(d,p) basis set for SCF and B3LYP, respectively. By MP2/cc-pVQZ//MP2/6-31G* calculation, Tsuzuki et al. obtained E0Δ and 9E0Δwere 9.54 and 8.91 kJ/mol, respectively [5]. The best calculated values from Johansson and Olsen by coupled cluster including single and double excitations as well as triples correlations (CCSD(T)) from density functional theory (DFT) were ΔE0 = 7.96 kJ/mol and ΔE90 = 8.79 kJ/mol, respectively [6]. In general, ΔE90 of biphenyl could be calculated to be very close to the experimental result by low level of quantum mechanism calculation. However, high level of quantum mechanism calculation made ΔE90 of biphenyl away from the experimental data. Thus, HF/6-31G** level was good enough for calculation of ΔE90 of biphenyl.
On the other hand, the calculated ΔE90 of biphenyl was difficult to match with the experimental data. Complicated levels of calculations not only lowered 0 ΔE of biphenyl yet increased ΔE90 of biphenyl. Therefore, ΔE90 (rotational barrier of biphenyl from φ = 450 to φ = 900) and 0 ΔE (rotational barrier of biphenyl from φ = 45o to φ = 00) might be dominated by two different mechanisms. In order to test this ideal, ten 4,4’-disubstituted biphenyls [1-10] (Figure 1) [7-9], which were potent inhibitors of acetylcholinesterase, butyryl cholinesterase’s and lipase, were chose to calculated 0 ΔE and ΔE90 by HF/6-311G(d,p) method [10]. The reason why we chose 4,4’-disubstituted biphenyls for this study was because steric effects from 4,4’-positions for these compounds were most insignificant while the electronic or polar effect from these positions were important for these conformational (rotational) changes.
4-Acyloxy-4’-N-n-butylcarbamyloxy-biphenyls (1-10) were synthesized from biphenyl [7-9]. All DFT calculations were preformed from B3LYP method and basis function of 6-311G(d,p) by Gaussian 03 [10]. MM-2 energy minimization was performed by CS Chem 3D (version 6.0). Origin (version 6.0) was used for linear and nonlinear least-squares curve fittings ΔE90 .
The minimized energies (Emin’s) of compounds 1-10 (except 9) calculated by HF/6-311G(d,p) method (Table 1) were linearly correlated with Hansch electronic values [11] (Figure 2). Thus, all electronic effects of all substituents were taken into consideration in HF/6-311G(d,p) calculation. Similar to the rotational spectroscopy for end-over-end rotation, rotational energy (EJ) was quantized as Eq. (1), where J and I were rotation quantum number (J= 0, 1, 2, 3,…) and moment of inertia, respectively [12].

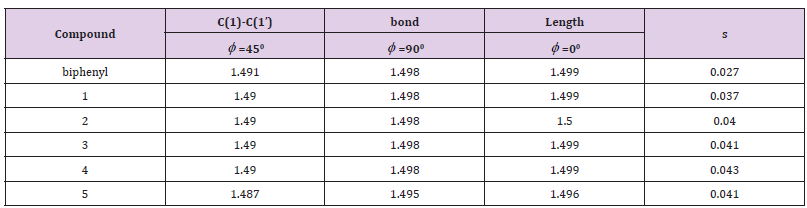
Table 1: Dihedral angles (φ ’s) and minimized energies (Emin’s) for the ground states of biphenyls and energy barriers for rotations of biphenyls from φ = -450 to 450 through 00( 0 ΔE ) and from φ = 450 to 1350 through 900 ( ΔE90 ) about the center axis.
The moment of inertia (I) might be written as Eq. (2), where R and m’ were rotated distance and reduced mass, respectively.
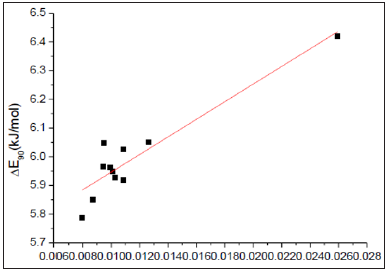
was linearly correlated with the inverse of reduced mass (1/m’) (Figure 3). Therefore, rotation of biphenyl from dihedral angle of 45∘to 90∘was just a simple physical rotation of an object about its center axis. Hence, both electronic and steric effects were insignificant in this mode of rotation.
Figure 3: A linear correlation between ΔE90 and 1/m’ of biphenyl and compounds 1-10 ΔE90 = (5.63±0.05)+(31±4)/m’ (kJ/mol) ; R=0.92355; residual sum of squares=0.03515.
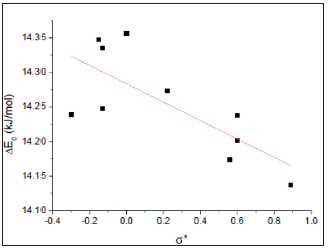
On the other hand, DE0 of biphenyl was not a simple physical rotation of an object about its center axis. A chemical reaction namely atropisomerization was occurred since the symmetry of the molecule is changed during this rotation as the conversion of R- to S-1,1’-bi-2-naphthyl-2,2’-diol. 0 ΔE was fairly correlated with Hammett substituent constant (σ * ) [13] (Figure 4). Therefore, the electronic effect played a role in this mode of rotation as those in six molecules with one ratable dihedral angle: ethane, methylamine, methanol, hydrazine, hydroxylamine, and hydrogen peroxide [14]. Negative ρ *value (-0.13) for this correlation indicated that the transition states (φ = 0o) were more positive charges than ground states (φ = 450) for these rotations. Electronwithdrawing substituents at the 4 or 4’ position of biphenyls would facilitate these rotations. Small absolute value of ρ * implied that the electronic effect occurred far away from the pivot bond of the rotation (C(1)-C(1’)).
Figure 4: A linear correlation between ΔE0 and σ * 0 ΔE = (14.28±0.02)-(0.13±0.04) Δ* (kJ/mol); R=0.70694; residual sum of squares=0.0220.
DFT calculated this activation energy by calculation of the energy difference between ground (dihedral angle, φ = 450) and transitional (dihedral angle, φ = 00) states. In other words, this method calculated the reaction as a concerted one-step reaction through a single transition state without a dramatic change in bond length of the C(1)-C(1’) pivot bond (Table 2) and (Figure 5). Therefore, 0 ΔE was equal to Δ E90 (rotation energy from physical properties) plus Δ Evib, where Δ Evib was the vibrational energy at the mass center near φ = 00.

Figure 5: one side of the fenced permanent plot (photo by Giday, 2013 left and Gebremichael Yiebyo on 19/11/2016 right).
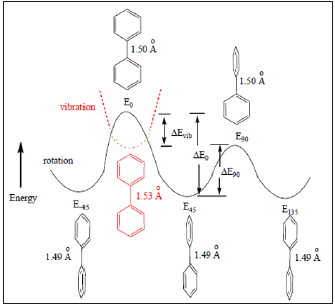
Table 2: Calculated the C(1)-C(1’) bond lengths of biphenyls for dihedral angles φ = 00, 450, and 900and the maximum bond length difference ( Δ x) for the C(1)-C(1’) bond stretching at φ = 00 (in Å).
However, the transition state of any reaction could not be actually detective by any method because the life time of the transition state was too short. Thus, ΔE0 of biphenyl from experiment was not the activation energy for a single step atropisomerization reaction (Figure 5). Instead, a two-step (two transition states and one intermediate) reaction was proposed for the rotation of biphenyl about its center axis from φ = -450to 450 through 00. At dihedral angle near 0∘, the principle of least motion [13] predicted that vibration (or stretching) of the pivot axis, the C(1)-C(1’) bond would be more favorable than twisting of the bond. Vibrational energy (Evib) could be expressed as Eq. (4), where Δ and k were the vibrational quantum number ( Δ = 0, 1, 2, 3, …) and force constant, respectively [12].
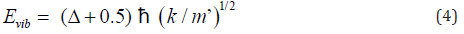
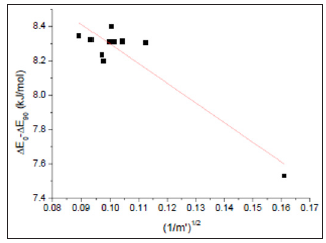
Thus, vibrational energy was inversely proportional to the root of reduced mass. A linear correlation between 0 ΔE90 − ΔE and (1/m’)1/2 of biphenyl and compounds 1-10 was observed (Figure 6). Hence, both physical rotation and vibration (or stretching) of the C(1)-C(1’) bond played important roles for rotation of biphenyl about the C(1)-C(1’) pivot bond from φ = -450 to 450 near φ = 00. The differences in the C(1)-C(1’) bond lengths for the stretching of biphenyl and compounds 1-10 near φ = 00(x’s) were calculated to be 0.027-0.046 Ǻ according to Hooke’s law, (1/ 2) vib ΔE = k Δ x2 (Table 2). Hence, the equilibrium C(1)-C(1’) bond length of the intermediate for rotation from φ = -450 to 450 near 0∘was about 1.53 Å (Figure 5). Thus, experimental 0 ΔE value of biphenyl (6.0 kJ/ mol)1 was the about the calculated ΔE90 value (6.4 kJ/mol).
Figure 6: A linear correlation between 0 ΔE90 − ΔE and (1/m’)1/2 of biphenyl and compounds 1-10. ( ) ( )( )1/2 0 ΔE90 − ΔE = 9.4 ± 0.2 − 11.5 ±1.5 1/ m’ (kJ/mol); R=0.9187; residual sum of squares=0.08063.
The authors acknowledge receipt of a grant from the Ministry of Science and Technology (MOST 107-2218-E-468 -005 - and 107- 2622-E-468 -002 -CC2) of Taiwan. The authors declare that they have no conflicts of interest.s


