Improved Thermal Ablation of Tumors Using A Real-Time Local Data Measurement System Volume 11 - Issue 5

Idir Mellal*, Youcef Fouzar, Aziz Oukaira, Emmanuel Kengne and Ahmed Laklissassi

• Department of Computer and Engineering, UQO university, Canada

Received: November 22, 2018;   Published: December 06, 2018

*Corresponding author: Idir Mellal, Department of Computer and Engineering, UQO university, Canada

DOI: 10.26717/BJSTR.2018.11.002156

Abstract PDF

An innovative approach based on the biochip technology for real-time monitoring of a thermal therapy applied in oncology is proposed in this paper. The proposed system provides two primary functions: real-time tracking of the targeted tissue’s thermal diffusion while at the same time locally characterizes and provides the parameters of the tissue. To validate our new approach, we use the Finite Difference Method (FDM) to solve the problem numerically and accurately predict the variation of the temperature. Numerical simulation results confirmed the efficiency of such an approach. Moreover, a hardware implementation of the discretized Bio Heat Transfer (BHT) Model using a Field Programmable Gate Array (FPGA) board was successfully achieved. The hardware implementation demonstrates that the proposed system can predict the future variation of the temperature readings and locally characterizes the tissue, allowing the user to adjust safely to subsequent injection doses. This new system shows promise in improving the efficiency of thermal therapy in oncological practice.

Thermal therapy has been approved as an effective treatment for many diseases, especially in cancerous tumors [1,2]. This therapy was born a long time ago, and it has been improved and entertained for decades. Nowadays, different techniques involving thermal therapy principles are available. We can categorize these techniques into diverse groups following the nature of the injected energy and the modality of administration. It contains among others the sources using Electromagnetic (EM), Ultra Sound (US) and Radio Frequency (RF). Thermal therapy, known commonly as thermotherapy, uses heating sources as well as cooling sources [2]. Real-time monitoring of a thermal therapy used for cancer treatment can improve the efficiency of the treatment and reduce damage to healthy tissue surrounding the targeted tumor. For this reason, different systems based mostly on image processing and sensors network, are used nowadays.

Although a significant development was accomplished in the technological devices and numerical methods, the thermal therapy still suffers from a lack of precision and high accuracy. Significant collateral damage will, indeed, occur during the thermal treatment procedure. This collateral damage could be fatal for the patient.

For this reason, a new technique has been developed to control the injected power for the purpose to minimize the risk of overheating the healthy surrounding tissue. This technique is known as dosimetry which is associated with an imaging system as Magnetic Resonance Image (MRI) for monitoring the delivered power. This novel approach, MRI-guided thermal therapy, has been widely deployed in the last decades [3,4].

Despite the developments in technological devices, modeling and simulation tools, the lack of precision and accuracy of thermal therapy could result in significant damage to healthy tissue surrounding the targeted tissue. Hyperthermia is particularly challenging due to the lack of visual cues such as thermal ablation or coagulation. In response to the imprecision of thermal therapy, researchers have worked to improve technological devices, numerical modeling, and simulation tools. A technique known as dosimetry, which employs imaging systems, was developed to monitor and control the delivered power [5]. Many researchers investigated the limits of the MRI guided technique and simulation models. Kabil et al. [6] reviewed the past and present challenges of numerical modeling and simulation for medical device safety in

MRI. They showed the difficulties of designers to reproduce and simulate complex shapes. Other research works are investigating new methods for real-time monitoring and direct feedback especially with hyperthermia modality [7]. For this reason, researchers continue to explore methods to improve the clinical results of the thermal therapy by controlling the heating source parameters, while others seek alternative methods for obtaining real-time thermal therapy monitoring and tumor feedback.

One such approach requires the use of a sensor network for realtime monitoring of thermal therapy. Schena et al. [8] overviewed the fiber optic sensors for temperature monitoring during thermal treatments. They described the advantages, flexibility, and ease of using fiber optic sensors for monitoring temperature during thermal treatments. Tosi et al. [9] used the optical measurement techniques based on different optical sensors to evaluate the temperature distribution and the pressure during an RF ablation process. They demonstrated the promise of these techniques for minimizing the damage of healthy tissue during thermal therapy. Other research works have been done using sensor networks for real-time monitoring of thermal therapy [10-12]. However, other approaches using biosensors, biomarkers and microfluidic devices offer enormous potential for treatment and early detection of tumorous cells. These devices also enable the tracking of disease progression and recurrence [13-16].

In this paper, we propose an innovative approach to thermal therapy monitoring in cancer treatment based on bio-microchip technology. The proposed system can work in real-time to take localized measurements of a tissue’s parameters and predict the evolution of its temperature to, safely, monitor the thermal treatment process. These local measurements improve the accuracy of treatment administration and reduce the potential damage to healthy tissues. To accomplish this, a smart module consisting of bio-probes and temperature sensor characterize the tumor at some points along its perimeter to determine the tissue’s temperature and other parameters. Then the data collected by the miniature biochip will be transmitted by a Radio Frequency Identification (RFID) module to the user to adjust the next injected dose.

To realize this biochip, we should imperatively start by developing a prototype and verify the feasibility and the functionalities of the designed system. Therefore, the hardware solution of the Bio Heat Transfer (BHT) equation was successfully implemented and verified based on the Virtex 6 FPGA board. With the boom of the semiconductor industry during the last two decades, biochip technology along with its developed implants has been found useful in many medical applications, including monitoring and diagnosing diseases, detecting undesirable agents, and delivering therapeutic drugs [13,17-20]. Nowadays, the biochips implants proved their efficiency in many treatments. In 2017, Mirela et al. [21] developed a personal electro-microfluidic platform allowing users to develop and program their bio-applications. The platform is controlled by an automated software with a simple graphical interface.

This study proposes a new approach based on bio-implants for Real-time monitoring of the thermal therapy applied in oncology for the removal of tumors. We performed the numerical modeling and simulation using MATLAB and COMSOL Multiphysics. To further verify the feasibility and functionalities of the proposed bio-microchip system, we implemented a hardware prototype using a field-programmable gate array (FGPA). The test results extracted from Xilinx Virtex-6 Board implementation are reported in this paper. The remaining of the paper is organized as follows. Section two presents the theoretical model and the fundamentals of monitoring based on biochip technology. Section three shows the proposed hardware architecture implementation and measured results. Section IV complete the paper with the conclusion.

The Bio Heat Model: Pennes’ Equation

The BHT equation governing temperature distribution in biological tissue was proposed by Pennes in 1948 [22]. This equation has been modified and improved by many researchers [23]. Despite the limits of the Pennes model, it is still the most used [24]. For x ϵ Ω and t > 0, Pennes’ equation is presented as follows:

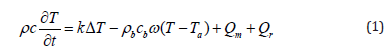
where ρ, c, and k are, respectively, the density (kg/m3), the specific heat (J/kg K), and the thermal conductivity (W/m k) of the tissue. T is the local tissue temperature T (x, t) in (K) with 0 ≤ x ≤ L. x = 0 corresponds to the skin surface, and x=L is the inner boundary. Ta is the arterial blood temperature (K). ρb and cb are the density and specific heat of the blood, respectively. The perfusion rate is represented by ω (ml/ml/s). Qm is the metabolic heat production per volume (W/m3). Qr stands for the deposited energy per volume. In this study, we utilized an RF probe as an external heating source that produces pulses with a duration of 2.5 s. The left-hand side of Equation (1) refers to the stored energy. The first term on the right-hand side stands for the energy diffusion within the tissue; the second term describes the thermal energy exchange between the blood and the surrounding tissue, due to blood convection.

The damage equation (2) was proposed in 1947 by Moritz and Henriques. COMSOL Multiphysics uses this equation to assess and quantify the damaged tissue [25-27].

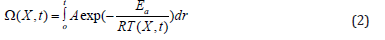
where ξ is the pre-exponential factor (s-1), R is the universal gas constant, 8.314 (J/(mol·K)), Ea is the activation energy to start cells kill (J/mol), and T stands for temperature (k).

The Initial Condition (IC) is given in equation (3):

Due to the difference in biological activities between the tumor and the healthy surrounding tissue, the temperature of the tumor is always higher than that of the healthy tissue. For this reason, thermography provides an efficient method for tumor detection [28].

The Boundary Condition (BC) associated with the extremity x=0 is a Neuman-type BC. We imposed a heat flux as a heating source. It is given in equation (4):

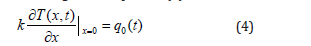
where q0(t) is the heat flux, and k is the thermal conductivity at x=0.

For x=L, we used a Dirichlet Type BC. The temperature is equal to the core tissue temperature, Tc. It is given in equation (5):

where Tc is the tissue core temperature, Tc=310 K.

The choice of these conditions is due to local constraints of the tumor. The temperature of the healthy neighboring tissue is maintained constant.

Finite Difference Method Discretization

To realize a hardware implementation of equation (1), we used the Finite Difference Method (FDM) to discretize it. The FDM was preferred over the other methods, like the Finite Element Method (FEM) or Finite Volume Method (FVM), because of its simplicity, short time development, and efficiency [29]. The FDM was proposed for the first time by Yee in 1969 [30] for the electromagnetic computing. His paper did not have a significant impact until the beginning of the technological boom in computer speed and memory capacity. The FDM needs a lot of parallel computing and considerable memory space. Therefore, the FDM has seen extensive utilization with the technological advances of the 1990s [31].

In this section, we present a discretization formula for One- Dimension (1D) Pennes’ equation. We discretized the main equation (1), the initial condition (3), and the boundary conditions (4-5). Th e purpose of the discretization is to realize a hardware implementation. The hardware implementation of the 3D model is a huge task. Indeed, the complexity of the biological tissue in which the parameters are anisotropic imposes on us to use a 1D approximation of the model. The proposed approximation in this work is based on 1D Pennes’ equation (1) for Ω = 0, L. The 1D simplification was chosen to simplify the hardware implementation and prove the feasibility of the method. We used the Finite Difference Method- Forward Time Centered Space (FDM-FTCS) method to approximate the solution.

Using the FDM-FTCS approximation of the Pennes equation, we can find the value of the temperature at the next state “n+1” at any point “i”. The algorithm will use the known values of the same point “i” and the two direct neighbors (“i-1” and “i+1”) at the present state “n”. Equation (6) shows the value of the temperature of any point “i” at the next state (n+1).

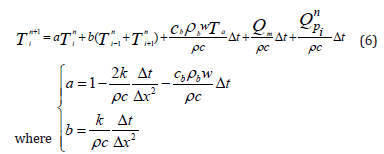
The Initial Condition (IC) and the Boundary Conditions (BC) used for the simulations are described as follows in equations (7- 9)). At x=0, the BC governing the boundary is:

where q0(t) represents the function of the heat flux produced by the external heating source.

At x=L, we assumed that the temperature is equal to the central tissue, Tc.

The initial temperature of the tissue is taken as a constant for all the domain.

Hardware Implementation of the FDM

To verify the functionality and the feasibility of such an approach, we proposed an FPGA hardware implementation of the 1D FDM approximation of the BHT equation. In fact, because of the high parallelism of the FDM and the enormous number of computing operations, the hardware implementation of the FDM is a tedious and complicated task to achieve on a single chip. The management of memories and the updating of each point in the grid is a considerable challenge that reduces the speed of execution and increases the used resources. Consequently, the hardware implementation of the FDM was a tough task for many years. The first hardware implementation was realized by Marek and al. [32] in 1992. However, the lack of powerful computers and large memory limited the performance of his architecture. In 2002, Schneider [33] and Placidi et al. [34] proved the feasibility and efficiency of the hardware implementation of the FDM. Since this date, many other works treating the hardware implementation of the FDM have been published [35,36]. To implement the hardware of the 1D FDM Pennes’ equation, we proposed an architecture based on simple components such as adders, multipliers, and register.

New Approach based on Biochip Technology for Real- Time Monitoring of Thermal Therapy

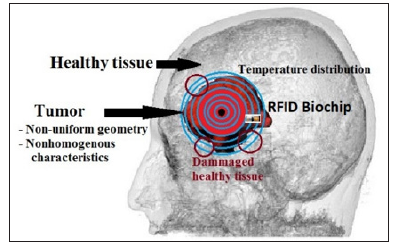
The challenge of thermal therapy for cancer treatment is to use enough power to destroy the cancerous tissue while minimizing collateral damage to the surrounding tissue. As the amount of power injected increases, so too does the margin of healthy tissue that may become damaged. In this approach, the intended biochip is supposed to monitor in real time a thermal therapy process to kill the tumorous tissue and save the healthy tissue surrounding the target. Because the diffusion of the heat in the tissue continues beyond the tumor boundary, dosimetry has been widely explored as a means of controlling the dose of the delivered power [37, 38]. Figure 1 shows an example of a real brain tumor with temperature iso-contour distribution on the tissue using one central heat source. To destroy the entire tumor, the clinician should inject more power while minimizing damage to the surrounding tissue. An imaging system is used to position the biochips with precision.

Figure 1: Brain tumor with a nonstandard geometry and nonhomogeneous characteristics. To ensure the destruction of the whole tumor, the therapist must inject more power. However, the diffusion of heat in healthy tissue creates collateral damage. The RFID biochips placed around the tumor follow the temperature distribution in real time and locally measure the tumor parameters.

The margin of the healthy tissue damaged during thermal therapy depends on the injected power. For this reason, we propose this real-time system to monitor the temperature distribution and control the injected power. Our approach is original and entirely different from what is used and available in the literature. It is based on feedback collected by biochips placed in the targeted tissue. The primary purpose of our system is to save the healthy tissue neighboring the tumor while destroying the malignant cells. Common approaches suggest that the shape of tumors is standard, such as a cylinder or cube. The physiological properties of a tumor are mostly taken as a space-dependent simple function or as a constant [4,20,39].

Figure 2: Different parts of the biochip implant. It includes four parts: bio-probes, temperature sensor, RFID module, and a smart unit. The temperature sensor and the bio-probes characterize the tissue locally in real time. These measurements will be used for better temperature diffusion calculation.

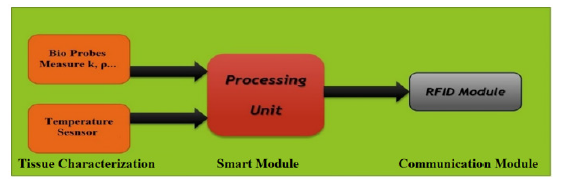
We propose a biochip-based implant system for maximizing the efficacy of cancer treatment while minimizing harm to healthy tissue. Biochip implants will be inserted all over the tumor, providing real-time data for the entire tissue mass. The positioning of the biochip depends on the complexity of the shape of the tumor. The positions are selected in a way that they cover the entire tumor especially the corners and the angles. The goal in doing this is to prevent the overheating of the adjacent tissue. The implants will characterize the tissue and monitor its temperature. They will then process the data and inform the user of the next dose of power to inject. Figure 2 shows the components of the biochip implant: Integrated thermal probes for local tissue characterization, a temperature sensor for local temperature measurements, and an RFID module for communicating with the user

Based on BHT, each biochip predicts the future temperature at some points to evaluate the next required dose to deliver. Also, it defines the local characteristics of the tissue and measures the local temperature in real-time using a miniature bio-probes and temperature sensor are integrated. The bio-probes perform a realtime measurement using a needle tip. Many works for real-time measurement of the tissue parameters have been done. Overall, the sensory bio-probes are a promising approach for direct and real-time tissue characterization. They are of great value to the characterization of tissues for thermal therapy, and other thermalbased clinical diagnostics and treatments [40-42]. Finally, the RFID module is used to communicate with the user.

Presentation of the New Thermal Monitoring and Dosimetry System

Figure 3: The components of the real-time monitoring system: The biochip, the heat source, and the control console. The system measures the local temperature, characterizes the tissue, and sends the data to the user. The user reviews the data and adjusts the injected data to destroy the cancerous cells and preserve the surrounding healthy tissue

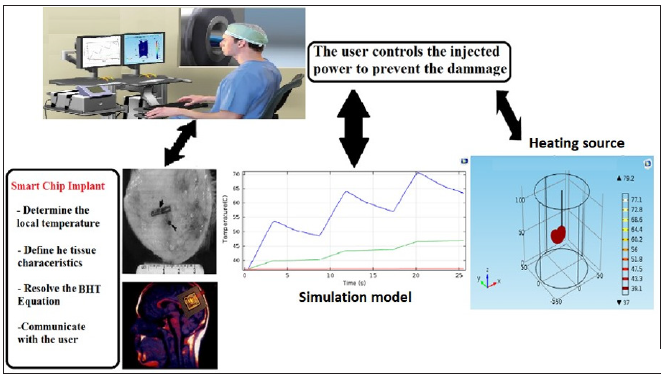
In this paper, we propose a new approach to cancer thermotherapy using a biochip system that performs real-time monitoring of thermal diffusion. The biochip implant is the central element of the proposed system. It predicts the tissue’s temperature, defines the tissue’s characteristics, and communicates this data to the user. Furthermore, parallel modeling and simulation of the process should be done with the real data of the tissue collected locally by the biochip probes and sensors. To supervise the process, the user follows the real-time evolution of the temperature in the biological tissue. This data enables the user to modify the injected power and adjust the heating source’s settings. The biochip system predicts the future temperature of specific points of the tissue by solving the BHT equation locally. The system measures the local temperature at these points, characterizes the targeted tissue, and sends the data to the user. Figure 3 describes the components of the real-time monitoring system: the biochip, the heat source, and the control console.

Table 1: Tissue parameters.

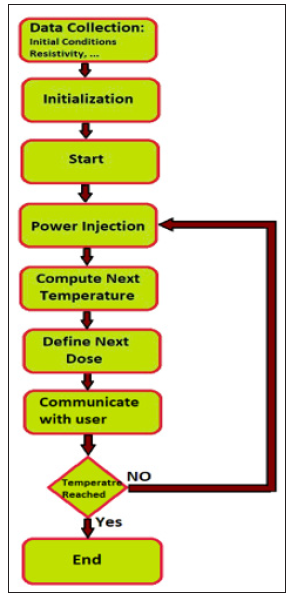
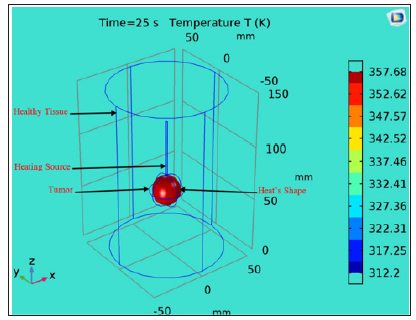
We numerically simulated the biochip system process based on actual tissue parameters measured by the integrated bio-probes. By using the measurements from the local tissue, we can ensure higher precision and higher computational accuracy. Indeed, increased precision improves therapeutic outcomes due to less damaged tissue. Figure 4 explains the treatment process using the biochip’s real-time monitoring system. We developed a 3D model using COMSOL Multiphysics to simulate an RF ablation of a brain tumor surrounded by a healthy tissue. The tumoral tissue represents the target to be ablated and removed. The surrounded healthy tissue should be spared and preserved. To do so, we should entirely control the dose of the injected power during the treatment. As an example, the tumor was modeled as a sphere with a 15 mm radius, and the healthy tissue was modeled as a cylinder of 50 mm radius and 150 mm height. We used a probe connected to an electrode of 10 mm length and 0.9 mm radius with a cylindrical shape to overheat the tumoral tissue. The heat spread all over the neighboring tissue forming a spherical shape and causing a necrotic tissue. The physiological parameters used in his work are reported in Table 1.

Figure 4: Diagram of the treatment process using the biochip system. Step 1: The biochip measures the initial temperature of the targeted tissue and characterizes it. Step 2: The memory and registers with the measured temperatures are initialized. Step 3: The user begins the power injection to destroy malignant cells. Step 4: The power is injected. Step 5: The biochip calculates the expected temperature. Step 6: The biochip communicates the predicted value to the user. Step 8: The user sets the value of the next dose if required.

To improve the thermal treatment and increase the precision of the tumor removal, some researchers proposed new heating sources with different architectures and new approaches [43-45]. Figure 5 shows a 3D model of an RF tumor ablation to show how the heat diffusion can produce significant collateral damage on the surrounding healthy tissue. The heating source overheats the tissue and causes its destruction. The diffusion of the heat in the tissue can increase the temperature at the surrounding healthy tissue. To achieve a precise and accurate treatment and to reduce the margin of collateral damage; the bio-chip implant will perform a local and real-time measurement of the temperature using a Micro Electro Mechanical System (MEMS) sensor

Figure 5: shows a 3D model of an RF tumor ablation to show how the heat diffusion can produce significant collateral damage on the surrounding healthy tissue. The heating source overheats the tissue and causes its destruction. COMSOL 3D model for an RF ablation of a spherical brain tumor. The healthy tissue was modeled as a cylinder with 50 mm radius and 150 mm. The tumor was designed as a sphere with 15 mm radius where we inserted the heating source to overheat to the targeted tissue. With proper adjustment of the injected power, overheating will destroy only the tumoral tissue and save the healthy tissue surrounding the tumor.

Furthermore, the bio-chip will measure the local parameters of the tissue (thermal conductivity and density). Using these accurate measured data, the bio-chip will be able to predict the variation of the temperature and define the optimal dose to be injected and communicate with the user. In contrast to the imaging systems (MRI) used nowadays where an estimation of the temperature is performed by computers, the bio-chip implants placed around the tumor will measure locally and in real-time the temperature of the tissue. Moreover, they will define the local parameters of the tissue, like the thermal conductivity and the density, to perform a more precise calculation of the optimal dose to be injected.

Numerical simulation results

To verify the accuracy of the FDM approximation and the developed architecture, we simulated the BHT model with COMSOL Multiphysics. Figure 6 shows the temperature of the heated tissue after three successive pulses. The different values of the parameters used for the COMSOL and MATLAB simulations are inspired in the literature and previous works. Table 1 summarizes the different physiological properties of the brain tissue, blood, tumor, and electrode [27,43,46-48]. A MATLAB script was developed to simulate the 1D-FDM approximation of the BHT equation. For the domain Ω with L=0.03 and the final time tf=25s, we use the following parameters to define the space and time mesh: tf=N*Δt, L= M*Δx where N=1000 and M=30. We injected three successive pulses at x=0; then we simulated the temperature at x= 0.0001m. The final time is tf=25s. We tested four different scenarios that were centered around varying the amplitude and the duration of the pulse, as shown in Figure 7.

Figure 6: COMSOL modeling of the temperature profile after injection of three pulses. The RF probe is positioned within the tumor, and a succession of pulses of a duration of 2.5 s with an amplitude of 2 Watts are injected.

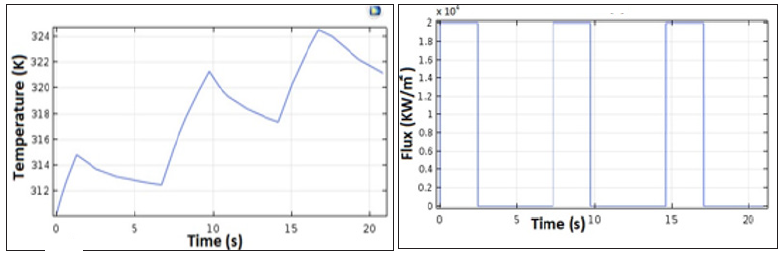
Figure 7: Numerical simulation results of the 1D BHT approximated by FDM-FTCS. We inject three successive pulses. The profile of the temperature corresponds to the expected thermal behavior. In (a) and (b), we injected three successive pulses with different pulse durations, 2.5 s in (a) and 1.7 s in (b), and we kept the amplitude of the pulse’s constant at 2k W/m2. We reproduced the same simulation by fixing the amplitude at 30 KW/m2 and varying the pulse duration as reported in (c) and (d) to 2.5 s and 1.7 s, respectively. The highest temperature was reached in (d) with the highest amplitude (30 KW/m2) and the larger pulse duration (2.5 s). The lowest temperature was registered in case (b) where the amplitude was fixed to 20 KW/ m2, and the pulse duration was 1.7 s.

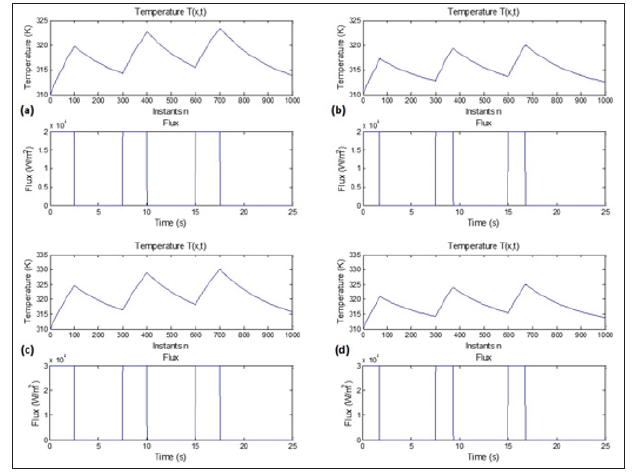
We used a combination of two different amplitudes, 20 KW/m2 and 30 KW/m2, and two different pulse durations, 2.5s and 1.7s. As a result, the temperature behavior changes as a function of the amplitude and the duration of the pulse. We measured the highest temperature in 6-c, where amplitude and pulse duration are the highest. The lowest temperature was noticed in the case 6-b, where the amplitude and the pulse duration are the lowest. We can clearly understand how the amplitude and the pulse duration infect the thermal behavior of the tissue.

Architecture of a Processing Element

Figure 8: PE’s structural diagram of one PE. The value of T (i, n). Each node of the grid is updated simultaneously. The architecture is composed only of simple components: Adders, multipliers, and registers. The value of each node ‘i’ is sent to the direct neighbors (‘i+1’ and ‘i-1’).

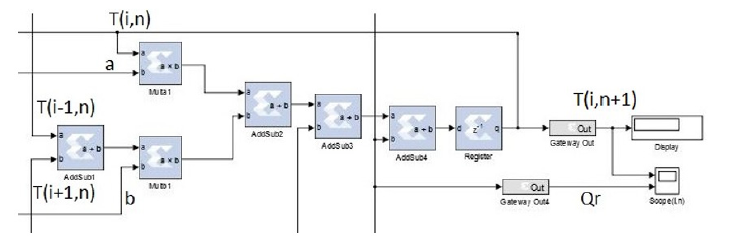
The hardware implementation of the model was realized on an FPGA Virtex 6 platform. The numerical simulations were performed with MATLAB and Simulink. The hardware’s architecture is composed of many Processing Elements (PE). Each PE computes the values of a specific node “n.” The PE consists of simple elements: Adders, subtractors, registers, and multipliers. The entire architecture of the system is composed of “n” PEs. Each PE computes the new value of the associated node, then updates its value. Each node of the grid updates its value simultaneously. Figure 8 depicts the architecture of one PE.

The results of the simulation are reported in Figure 9, which shows the temperature response after injection of three pulses. As expected, the values the prototype returned correspond to the temperatures predicted by the FDM implementing the BHT equation. The results reported by the COMSOL simulations, in Figure 6, and the results predicted of the bio-chip, in Figure 9, have similar thermal behavior. After three successive pulses, the highest temperature reached is around 325 K in both cases. Even though we can see a few differences between the two figures due to the different data type used in both cases and different algorithms, where COMSOL uses the Finite Element Method (FEM) and the FPGA implementation is based on the FDM method, we have proven that the prediction made by the FPGA prototype of the bio-chip is approximately the same as the simulated results made by COMSOL.

Figure 9: Simulation results: The temperature response after the injection of three pulses. The rise of temperature is due to the injection of the power. During the relaxation time, the temperature decreases gradually till the next pulse is injected.

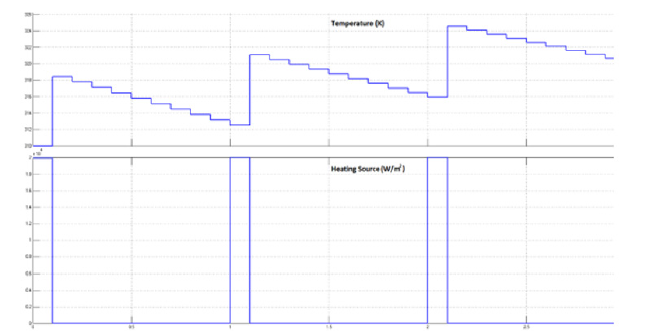
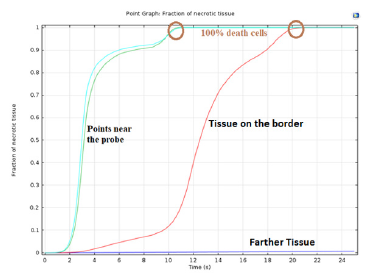
Figure 10. shows a fraction of necrotic tissue visualized by COMSOL Multiphysics. Cell destruction approaches 100% as the cells approach the heat source. Closer to the heat source, total cell death occurs in less than 10 s, destroying the tumor. The rate of cell death is slower near the border of the tumor, which preserves the surrounding healthy tissue.

Figure 10: Tissue destruction rate. The points of the tumor surrounding the heat source reach destruction faster than the points on the border with the healthy tissue. The healthy tissue not directly adjacent to the tumor exhibit zero necrotic tissue. This tissue is spared and saved entirely.

A real-time monitoring system for thermal therapy applied in oncology domain was proposed and prototyped on FPGA Virtex 6 platform. The developed approach is based on the use of a biochip implant to monitor and control the thermal treatment. This biochip-based system includes three main blocks for measurements, prediction, and communication. The bio-probes module is intended to characterize the tissue locally. A temperature sensor is also integrated to measure the temperature locally in real time. Moreover, the smart module, which is the central element of the system, predicts the expected temperature variation in the targeted tissue in order to limit its effects to nearby healthy cells. Finally, an RFID module is used to communicate the data with the user. Before implementing the hardware architecture on an FPGA platform, we performed a numerical simulation with MATLAB and COMSOL Multiphysics. The results of the simulations with COMSOL and MATLAB show the similarity of the thermal behavior of the tissue. An FDM approximation of the Pennes’ equation solution has been implemented, and the results of all simulations were reported. The FPGA prototype proved the feasibility and efficiency of the proposed model. Real-time prediction of the temperature was performed and tested with the mentioned platform. The novelty of this system lies in the fact that it can accurately predict the variation of temperature in the targeted tissue and characterizes in situ the tissue locally and in real-time.

With this prediction, the radiotherapists can adjust the injected power to prevent possible significant collateral damage by manipulating the signal amplitude and exposure time. Using our proposed approach, we can reduce the possible damage to surrounding healthy tissue during the thermal treatment. Without MRI room, we believe that the proposed approach will be adopted by oncologists and radiotherapists for safety and low cost. With the use of the proposed bio-implant, we enhanced the precision and efficiency of the treatment and improved the quality of the treatment with the highest accuracy. Further research can be done to design the final prototype of the biochip system and integrate its different parts. Experimental validations of the designed system can be done using ghost tissue.

1. Huang WH, Liauh CT (2012) Review: Therapeutical applications of heat in cancer therapy. J Med Biol 32(1): 1-10.
2. Mellal I, Oukaira A, Kengene E, Lakhssassi A (2017) Thermal therapy modalities for cancer treatment: A review and future perspectives. Int J Appl Sci Res Rev 4(2): 14.
3. Rezapour M, Leuthardt EC, Gorlewicz JL (2016) Design of a steerable guide for laser interstitial thermal therapy of brain tumors. J Med Dev 10(3): 030909.
4. Habash RW, Bansal R, Krewski D, Alhafid HT (2006) Thermal therapy, part 2: Hyperthermia techniques. Crit Rev Biomed Eng 34(6): 491-542.
5. Kabil J, Belguerras L, Trattnig S, Pasquier C, Felblinger J, et al. (2016) A Review of numerical simulation and analytical modeling for medical devices safety in MRI. Yearb Med Inform 10(1): 152-158.
6. van Rhoon GC, Paulides MM, van Holthe JM, Franckena M (2016) Hyperthermia by electromagnetic fields to enhanced clinical results in oncology. Conf Proc IEEE Eng Med Biol Soc 2016: 359-362.
7. Emiliano Schena, Daniele Tosi, Paola Saccomandi, Elfed Lewis, Taesung Kim (2016) Fiber optic sensors for temperature monitoring during thermal treatments: An overview. Sensors 16(7): 1144.
8. Tosi D, Macchi EG, Cigada A (2015) Fiber-optic temperature and pressure sensors applied to radiofrequency thermal ablation in liver phantom: Methodology and experimental measurements. J Sensors 2015: 22.
9. Caponero MA, Polimadei A, Ariano M, Schena E, Massaroni C, et al. (2017) Fabrication and calibration of three temperature probes for monitoring the effects of thermal cancer ablation. IEEE International p. 1-5.
10. Schena E, Saccomandi P, Fong Y (2017) Laser ablation for cancer: Past, present and future. J Funct Biomater 8(2): 19.
11. Kühlbach C, da Luz S, Baganz F, Hass VC, Mueller MM (2018) A microfluidic system for the investigation of tumor cell extravasation. Bioengineering 5(2): p. E40.
12. Bavli D, Prill S, Ezra E, Levy G, Cohen M, et al. (2016) Real-time monitoring of metabolic function in liver-on-chip microdevices tracks the dynamics of mitochondrial dysfunction. Proc Natl Acad Sci USA 113(16): E2231-E2240.
13. Tothill IE (2009) Biosensors for cancer markers diagnosis. Semin Cell Dev Biol 20(1): 55-62.
14. Flepisi BT, Bouic P, Sissolak G, Rosenkranz B (2014) Biomarkers of HIVassociated Cancer. Biomarker Cancer 6: 11-20.
15. Marcomini KD, Fleury EFC, Oliveira VM, Carneiro AAO, Schiabel H, et al. (2018) Evaluation of a computer-aided diagnosis system in the classification of lesions in breast strain elastography imaging. Bioengineering 5(3): E62.
16. Shukla S, Agarwal AK, Lakhmani A (2016) MICROCHIPS: A leading innovation in medicine. IEEE International pp. 205-210.
17. Tan SJ, Lakshmi RL, Chen P, Lim WT, Yobas L, et al. (2010) Versatile label free biochip for the detection of circulating tumor cells from peripheral blood in cancer patients. Biosens Bioelectron 26(4): 1701-1705.
18. Lee M, Kim KH, Park JG, Lee JH, Lim HW, et al. (2012) Fabrication of a hydrophobic/hydrophilic hybrid-patterned microarray chip and its application to a cancer marker immunoassay. BioChip Journal 6(1): 10- 16.
19. Yi M, Panchawagh HV, Mahajan RL, Liu Z, Goldberg SN (2005) Micromachined electrical conductivity probe for RF ablation of tumors. American Society of Mechanical Engineers p. 53-56.
20. Alistar M, Gaudenz U (2017) Open drop: An integrated do-it-yourself platform for personal use of biochips. Bioengineering 4(2): 45.
21. Pennes HH (1948) Analysis of tissue and arterial blood temperatures in the resting human forearm. J Appl Physiol 85(1): 5-34.
22. Lakhssassi A, Kengne E, Semmaoui H (2010) Modifed pennes’ equation modelling bio-heat transfer in living tissues: Analytical and numerical analysis. Natural Science 2(12): 1375-1385.
23. Wissler EH (1998) Pennes’ 1948 paper revisited. J Appl Physiol 85(1): 35-41.
24. Henriques FC, Moritz AR (1947) Studies of thermal injury: I. The conduction of heat to and through skin and the temperatures attained therein. A theoretical and an experimental investigation. Am J Pathol 23(4): 530-549.
25. Dewey WC (2009) Arrhenius relationships from the molecule and cell to the clinic. Int J Hyperthermia 25(1): 3-20.
26. Garcia PA, Davalos RV, Miklavcic D (2014) A numerical investigation of the electric and thermal cell kill distributions in electroporation-based therapies in tissue. PloS one 9(8): e103083.
27. Pavithra P, Ravichandran K, Sekar K, Manikandan R (2018) The effect of thermography on breast cancer detection. 9(1): 10-16.
28. Kunz KS, Luebbers RJ (1993) The finite difference time domain method for electromagnetics. CRC press. pp. 464.
29. Yee K (1966) Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Transactions on antennas and propagation 14(3): 302-307.
30. Schneider JB (2010) Understanding the finite-difference time-domain method.
31. Marek J, Mehalic M, Terzuoli A (1992) A dedicated VLSI architecture for finite-difference time domain calculations. 8th Annual Review of Progress in Applied Computational Electromagmetics pp. 546-553.
32. Schneider RN, Turner LE, Okoniewski MM (2002) Application of FPGA technology to accelerate the finite-difference time-domain (FDTD) method. ACM pp. 97-105.
33. Placidi P, Verducci L, Matrella G, Roselli L, Ciampolini P (2002) A custom VLSI architecture for the solution of FDTD equations. IEICE Transactions on Electronics 85(3): 572-577.
34. Cattaneo R, Natale G, Sicignano C, Sciuto D, Santambrogio MD (2016) On how to accelerate iterative stencil loops: A scalable streaming-based approach. ACM Transactions on Architecture and Code Optimization (TACO) 12(4): 53.
35. Deest G, Estibals N, Yuki T, Derrien S, Rajopadhye S (2016) Towards scalable and efficient FPGA stencil accelerators. Proc IMPACT’.
36. Dewhirst MW, Viglianti BL, Lora-Michiels M, Hanson M, Hoopes PJ (2003) Basic principles of thermal dosimetry and thermal thresholds for tissue damage from hyperthermia. Int J Hyperthermia 19(3): 267-294.
37. Szasz A, Vincze G (2006) Dose concept of oncological hyperthermia: Heat-equation considering the cell destruction. J Cancer Res Ther 2(4): 171-181.
38. Kengne E, Mellal I, Lakhssassi A (2015) Bioheat transfer problems with spatial or transient heating on skin surface or inside biological bodies. Proc BMEI pp. 792-797.
39. Haemmerich D, Schutt DJ, Wright AW, Webster JG, Mahvi DM (2009) Electrical conductivity measurement of excised human metastatic liver tumours before and after thermal ablation. Physiol Meas 30(5): 459- 466.
40. Park J, Choi WM, Kim K, Jeong WI, Seo JB (2018) Biopsy needle integrated with electrical impedance sensing microelectrode array towards realtime needle guidance and tissue discrimination. Sci Rep 8(1): 264.
41. Yang CH, Li W, Chen RK (2018) Characterization and modeling of tissue thermal conductivity during an electrosurgical joining process. IEEE Transactions on Biomedical Engineering 65(2): 365-370.
42. Mellal I, Kengne E, El Guemhioui K, Lakhssassi A (2016) 3D modeling using the finite element method for directional removal of a cancerous tumor. Journal of Biomedical Sciences 5: 4.
43. Lau L, Han YL (2016) Exploring a novel heating probe design for tumor ablation 1. Journal of Medical Devices 10(3): 030930-030930-030932.
44. Fang Z, Zhang B, Moser M, Zhang E, Zhang W (2017) Design of a novel electrode of radiofrequency ablation for large tumors: A finite element study. ASME J of Medical Diagnostics 1(1): 011001.
45. Tungjitkusolmun S, Staelin ST, Haemmerich D, Tsai JZ, Cao H, et al. (2002) Three-dimensional finite-element analyses for radio-frequency hepatic tumor ablation. IEEE transactions on biomedical engineering 49(1): 3-9.
46. Panescu D, Whayne JG, Fleischman SD, Mirotznik MS, Swanson DK, et al. (1995) Three-dimensional finite element analysis of current density and temperature distributions during radio-frequency ablation. IEEE Trans Biomed Eng 42(9): 879-890.
47. Holmes K (2009) Thermal conductivity data for specific tissues and organs for humans and other mammalian species. Thermal Properties.
48. ITIS Foundation (2018) Tissue properties.