Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Alan Kleinman*
Received: September 10, 2018; Published: September 18, 2018
*Corresponding author: Alan Kleinman, PO BOX 1240, Coarsegold, CA 93614, USA
DOI: 10.26717/BJSTR.2018.09.001751
Random mutation and natural selection occur in a variety of different environments. Three of the most important factors which govern the rate at which this phenomenon occurs is whether there is competition between the different variants for the resources of the environment or not whether the replicator can do recombination and whether the intensity of selection has an impact on the evolutionary trajectory. Two different experimental models of random mutation and natural selection are analyzed to determine the impact of competition on random mutation and natural selection. One experiment places the different variants in competition for the resources of the environment while the lineages are attempting to evolve to the selection pressure while the other experiment allows the lineages to grow without intense competition for the resources of the environment while the different lineages are attempting to evolve to the selection pressure. The mathematics which governs either experiment is discussed, and the results correlated to the medical problem of the evolution of drug resistance.
Random mutation and natural selection (RMNS) are a phenomenon which works to defeat the treatments physicians use for infectious diseases and cancers. A good understanding of this phenomenon is required in order to make rational decisions on how to use these selection pressures to minimize the effect of RMNS and maintain the durability of these treatments. In references, "The basic science and mathematics of random mutation and natural selection" [1] and "The mathematics of random mutation and natural selection for multiple simultaneous selection pressures and the evolution of antimicrobial drug resistance" [2] the mathematics was derived for the evolutionary trajectories for a single selection pressure acting at a time and multiple simultaneous selection pressures respectively. In either case, it was shown that this stochastic process is governed by sets of nested binomial probability equations where each equation is linked to the others by the multiplication rule of probabilities. And the random trial for this stochastic process is the replication. Each evolutionary step requires the variant makes sufficient replications for there to be a reasonable probability for the next beneficial mutation(s) to occur and improve fitness against the particular selection pressure(s). This cycle of beneficial mutation(s) followed by amplification of the beneficial mutation(s) describes the physics and mathematics of RMNS. Are these governing equations for RMNS altered by the intensity of selection and how is RMNS affected in environments where there is competition between the variants for resources in the environment? These factors are analyzed by considering two important experiments testing the RMNS phenomenon. And how does recombination alter the evolutionary trajectory to a given selection pressure?
The empirical effects of competition on the RMNS phenomenon have been measured by an important and ongoing experiment, the E. coli long-term evolution experiment (LTEE) led by Richard Lenski that has been tracking genetic changes in 12 initially identical populations of asexual Escherichia coli bacteria since 1988. The experiment consists of 10ml vials that contain a glucose- limited medium which selects for the most energy efficient variants in the population. Each day, 1% of the population in each vial is transferred to fresh vials. This gives enough energy resources to the population to give about 6 to 7 population doublings per day. About every 500 generations, samples are preserved to give a record of the evolutionary process. It is recognized that this competition between different variants slows the adaptation process in this experiment [3]. On the other hand, Kishony and his co-workers have devised a different environment to investigate the RMNS phenomenon. Environments which don't impose intense competition between variants is being studied by Kishony and his co-workers. [4]. In this study "we introduce an experimental device, the microbial evolution and growth arena (MEGA)-plate, in which bacteria spread and evolved on a large antibiotic landscape (120 x 60 centimeters) that allowed visual observation of mutation and selection in a migrating bacterial front."
These experiments consist of large Petri dishes where the east and west edges of the dishes do not have any antibiotic in the medium but as one moves from either the east or west to the middle of the plate, increasing concentrations of the antibiotics are instituted in north/south bands on the Petri dish. Bacteria are inoculated on to the plates, colonies initially grow in the antibiotic- free regions but as the colonies grow, mutant variants in the colonies are able to migrate and grow in the increasing drug concentration regions. In contrast with the Lenski experiment, the colonies in the Kishony experiment are not forced to compete with each other The colonies only need to grow sufficiently (achieve sufficient replications) for the improved fitness variants to appear for each succeeding drug concentration region. The Kishony experiment provides sufficient resources for each clone to achieve the number of replications needed for the RMNS cycle of beneficial mutation/ amplification of beneficial mutation process to work. Competition between colonies only occurs when the colonies collide and must now start competing for resources, but population sizes achieved at this point are already much larger than in the Lenski experiment.
Clearly, the Kishony experiment would not work with a standard size Petri dish, the energy limitation of the small dish preventing the colonies to grow large enough for RMNS to operate. A simple way to understand how competition between variants slows the RMNS phenomenon is to apply the principle of conservation of energy Each variant is on its own particular evolutionary trajectory. In order to have a reasonable probability of the next beneficial mutation occurring, a given variant must achieve sufficient replications. Consider an evolutionary environment which has energy resources which can support "N" replications in a population. If there is only a single variant in the population, that variant can replicate "N" times.
However, if there are two equally fit variants in the population, each variant will only be able to replicate "N/2" times. This is the circumstance faced by the populations in the Lenski experiment. His more fit variants must drive the less fit variants to extinction in order to achieve the number of replications necessary for the next beneficial mutation to occur. On the other hand, the Kishony populations are not competing with each other (until colonies collide) and exponential growth of the populations are achievable allowing for more efficient operation of RMNS. This does not affect the evolutionary trajectories in either case. Both trajectories still consist of nested binomial probability equations, the difference is in the ability of the variants to amplify at each evolutionary step. The Lenski experiment forces his populations to "fix" or "substitute" their beneficial mutations in the energy limited environment in order to achieve the replications required for RMNS to work.
In the Kishony experiment, fixation is not required for RMNS to operate. The difference in the two experiments highlights the two important ways in which natural selection operates with RMNS. In the Kishony experiment, only absolute fitness to reproduce is important for RMNS to operate. As long as a given colony of bacteria can achieve sufficient size, the probability of a beneficial mutation occurring will be reasonable and a mutant will appear which can grow in the next higher antibiotic concentration region.On the other hand, in the Lenski experiment, the differential fitness to reproduce, the ability of one variant to out-compete the other variants for the resources of the environment is acting in concert with the absolute fitness to reproduce. The battle for the resources in the environment slows the ability of the more fit variant to achieve the number of replications necessary for there to be a reasonable probability of another beneficial mutation to the selection condition. Until the more fit variant drives the less fit variant to extinction, amplification of the more fit variant will be delayed. In addition, once the more fit variant has driven all the other less fit variants to extinction, this more fit variant must still replicate sufficiently for there to be a reasonable probability of the next beneficial mutation occurring. Once that new, most fit variant appears, this new variant must now drive the old variant to extinction in order for the RMNS process to continue.
The mathematics which governs this part of the evolutionary process was addressed by Haldane in "The Cost of Natural Selection" [5] and Kimura's work, "On the probability of fixation of mutant genes in a population" [6]. We can, for example use the mathematics that Haldane worked out to estimate the intensity of selection for each beneficial mutation in the Lenski experiment during the competition phase of each evolutionary step. Haldane models the intensity of selection by counting the number of deaths of the less fit variant. He does this by summing up the number of deaths in each generation of the less fit variants. The governing equations from Haldane's paper [5] for a cloning population are repeated here for clarity: From the Haldane paper: Let the nth generation, before selection, occur in the frequencies

Here A and a are allelomorphic genes in a haploid, genotypes in clonal or self-fertilizing organisms, or different type of cytoplasm. If 1-k of a survive for every one of A, then the fraction of selective deaths in the nth generation is,
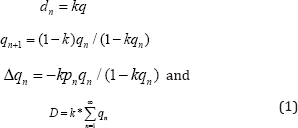
Where D is the fraction of selective deaths of the less fit variant, (1-k) is the number of less fit variants that survive for every more fit variant, "n" is the number of generations and qn is the relative frequency of the less fit variant." We can use equation (1) to estimate the intensity of selection for a competing population. Lenski in his paper Phenotypic and Genomic Evolution during a 20,000-Generation Experiment with the Bacterium Escherichia coli[7] estimated that there was between 10 and 20 beneficial mutations occurring in his populations. Using 20 beneficial mutations over 20,000 generations give about 1 beneficial mutation for every 1000 generations. The 10ml vials can support about e8 bacteria daily of which e6 bacteria are from the previous day's population. There are e8-e6 replications every day which represents between 6 and 7 doublings (or generations every day).If we use 7 generations per day, for 1000 generations, there will be about 1000 generations/7generations per day*(e8-e6) replications or approximately total replications 1.4e 10 replications for that fixation cycle.
To compute the number of replications resulting in deaths of the less fit variants, we need to estimate the number of replications of the more fit variant necessary to have a reasonable probability of the next beneficial mutation occurring in that 1000 generation interval. We can obtain this estimate by using the mean value of the binomial distribution. For a mutation rate of e-8, it will require about e8 replications of the more fit variant to have a reasonable probability of 1 beneficial mutation occurring. So, of the about 1.4e10 replications of Lenski's bacteria, only about e8 of those replications were of the more fit variant. The vast majority of the bacteria reproducing are of a lineage that is going extinct. This gives real meaning to Haldane's concept of the "cost of natural selection". We can now estimate the value of "k". D͌(1.4e10-e8)/1.4e10͌1, we can bracket the summation term by assuming that qn is 1 for n=1 to 1000 which will give a lower estimate for "k", the (1.4e 10-e8)/1.4e10͌k*e3 or k͌e-3. A more accurate estimate of "k" can be made by assuming a linear decrease in the relative frequency of qn over the thousand generations which would give a value k͌2e-3.
It is shown above that competition slows the RMNS phenomenon. But how does intensity of selection affect RMNS. Does increasing or reducing the intensity of selection alter the evolutionary trajectory? What does reduce or increasing the intensity of selection do to the evolutionary process of drug resistance? Reducing the intensity of selection allows more variants to survive and replicate. This principle can be illustrated with the Kishony experiment. His experiment has 4 regions of increasing intensity of selection. In order for the population to adapt to grow in an increased intensity of selection region, it requires a beneficial mutation. Call the beneficial mutation required for the lowest intensity of selection A, the next beneficial mutation B, the next C and the mutation for the extreme selection pressure D.
The only variant that can grow in all regions of the plate is the variant with all four mutations A, B, C, and D. The variant with mutations A, B, and C can grow anywhere on the plate except the extreme selection pressure region. The variant with mutations A and B can only grow in the two lowest intensity regions and the variant with only mutation A can only grow in the low-intensity selection pressure region. Now consider that Kishony does his experiment with only two regions on his plate, one area without any antibiotic and the other area with only the low concentration of antibiotic. The evolutionary trajectory to accumulate mutations A, B, C, and D will still be the same as if the experiment was done with areas of increasing intensity of selection.
Recombination is essentially the shuffling of alleles [8]. In references [1,2] the equations were derived assuming a clonal population. In other words, the number of replications used to compute the probability of a beneficial mutation was based on the replication of the entire genome. When recombination occurs, the allele which would benefit from the particular mutation is being "shuffled" to a different genome. To address this circumstance, the replication should not be thought of the entire genome but instead, the replication of the particular allele. The mathematics remains unchanged and this should make sense since the most studied example of RMNS, the evolution of drug-resistance of HIV to combination therapy shows no significant effect due to recombination.
The point of this exercise is to demonstrate how competition, conservation of energy, the intensity of selection and recombination impacts RMNS and the evolution of drug-resistance. The Lenski experiment demonstrates how his bacteria must compete with each other in order to evolve to the selection pressure, starvation. In fact, differential reproductive fitness is simply a restatement of the law of conservation of energy, as shown by Flake and Grant in their paper An Analysis of the Cost of Selection Concept [9]. However, RMNS is not a conservative phenomenon. It does not depend on the relative frequencies of the different variants in a population. In fact, different variants can be evolving to the same selection pressures where the different variants are taking their own particular evolutionary trajectories to improved fitness [10]. The key factor for this to occur is that each variant must have sufficient absolute reproductive fitness (able to do enough replications) for there to be a reasonable probability of the next beneficial mutation occurring. This is what is demonstrated in the Kishon experiment. This is also demonstrated in the Lenski experiment but is concealed within the competitive environment in which the experiment is run. Even though the Kishony experiment was not intended to be a direct correlation with the problem of drug- resistance in the clinical environment, this experiment correlates much better than does the Lenski experiment. A patient with an incompetent immune system such as those with leukemia or those taking immune suppressant drugs and suffering from an infection would correlate much more closely with what happens in the Kishony experiment than what happens in the Lenski experiment. It would seem that the immune incompetent patient would be most susceptible to a drug-resistant infection. But Tamma [11] and coauthors argue in their paper Combination Therapy for Treatment of Infections with Gram Negative Bacteria [11] that combination therapy does not prevent or inhibit the evolution of drug-resistance. They report "Finally, clinical studies of infections with Gram- negative bacteria have shown no difference in the emergence of resistance during antimicrobial therapy with combination therapy versus monotherapy."
The problem with this study is that many of their clinical studies involve Pseudomonas aeruginosa and gram-negative organisms. It is well known that Pseudomonas aeruginosa and other gram-negative organisms evolve resistance to drugs via an efflux pump [12,13]. This mechanism of drug-resistance can give resistance to antibiotics the organism has never been exposed to simply by the ability of the organism to pump out the toxic agent. To generalize this effect to all cases of drug-resistance misses the point of how to prevent drug resistance. Lopes and his co-authors in Prophylaxis with levofloxacin: impact on bacterial susceptibility and epidemiology in a hematopoietic stem cell transplant unit [14] report that prophylaxis with quinolones in their immune compromised patients reduces the incidence of gram-negative infections but at the expense of emergence of drug resistant variants. If the drug-resistance occurs simply by increasing the activity of an efflux pump is a different matter when considering the evolution of drug-resistance at individual metabolic pathways to individual drugs.
In the case drug-resistance by way of an efflux pump, the strategy for treatment of such infections should focus on ways of overwhelming the efflux pump. If drug-resistance occurs at the level of individual metabolic pathways as with methicillin-resistant Staphylococcus Aureus, strategies must be developed which prevent the accumulation of the mutations which would give resistance and the mathematics point to the use of combination therapy. This could easily be demonstrated with the Kishony experiment by using two drugs in each band rather than the single drug being used at this time. The growth of the resistant variants will be inhibited until beneficial mutations occur for each of the drugs occur in some member of the population. The multiplication rule of probabilities makes this a much lower probability occurrence. The key to prevention of drug-resistance is imposing a more complex evolutionary trajectory on the bacterial population.
Evolution is a complex process. It involves multiple different processes, each governed by their own particular mathematics. RMNS is only one part of the process but it is the key part. Competition between variants only slows this process. The intensity of selection affects the number of variants able to evolve to the selection conditions but does not alter the evolutionary trajectories to improved fitness. These trajectories will still consist of nested binomial probability equations where each equation is linked to the others by the multiplication rule of probabilities for random independent events. Recombination will shuffle alleles within variants in a gene pool but the evolutionary process for a particular gene by RMNS remains the same, that is the evolutionary trajectory for that gene will still consist of nested binomial probability equations linked by the multiplication rule of probabilities. A clear understanding of these processes is the key to developing strategies for defeating drug-resistance.


