Chaotic Motion of the Human Head-Neck System Volume 8 - Issue 1

Livija Cveticanin*

• Faculty of Technical Sciences, University of Novi Sad, Serbia

Received: July 25, 2018;   Published: August 16,2018

*Corresponding author: Livija Cveticanin, Faculty of Technical Sciences, University of Novi Sad, Trg D. Obradovica 6, 21000 Novi Sad, Serbia

DOI: 10.26717/BJSTR.2018.08.001600

Abstract PDF

Objectives: The aim of the paper is to give a new explanation of motion of human head-neck structure modelled as a nonlinear two-degree-of- freedom system. The influence of the excitation parameter on steady state motions (periodic and chaotic) is analyzed. A method for chaos control is discussed.

Methods: Mathematical model, given with two nonhomogenous and nonlinear coupled second order differential equations, is analyzed. The nonlinearity is assumed to be of any order given with a real number (integer or noninteger). For qualitative analysis of the motion the numerical simulation is applied. For determination of chaos the method based on the sign of Lyapunov's exponents and bifurcation diagram is used. Method of chaos suppression is incorporated into the investigation.

Result: Due to nonlinearity steady state periodic and chaotic motion may appear. The type of motion depends on the parameter of excitation which acts apart from the apparent mass modeling the human head. Chaos suppression is achieved with a control function added to the system.

Conclusion: Knowing the limits of excitation and biomechanical parameters, it is possible to obtain the type of the steady-state motion of the head as appointed mass. We think that the transition between steady-state motions is useful in explanation of the injury of head-neck system. It is believed that in the human body a control mechanism must exist which transforms the chaotic motion to a simple periodical steady state one.

It is known that vehicle accidents, degenerative diseases and also recreational activities may cause disorder in the human body special in the neck - head region. The usual symptoms of injuries are neck pain, fatigue and painful lesions [1]. In the most of studies it is stated that these symptoms are due to whiplash (a fast motion of the head and neck without a direct force exerted onto the head) which causes cervical spine disorder [2]. However, up to months or years of accident, headaches, as nonspecific symptoms, are reported. The reason for headache is already not known. Namely, the mechanisms of injury are not fully understandable. For the better insight of the evaluation of the injury risk the dynamics of the head-and-neck system needs further investigation. The aim of this paper is to introduce a new head-neck model, which includes the nonlinearity, with the purpose to give the appropriate qualitative analysis of the head motion which is without direct force attack.

It is expected that the study will give some highlights in the head injury. The mechanical model of the human body could be represented by a discrete oscillatory system (masses, springs and dampers) or a distributed parameter model. The number of degrees of freedom of discrete system, required in a model, strongly depends on the purpose of the model. Wei and Griffin [3] developed the biomechanical model of neck and head system as a single (o.d.f) or two degrees-of- freedom (t.d.f) ones. These models are not possible to describe internal movements of the body but are suitable to describe the head motion relatively to the neck. Simulations were made on models which help to understand the behavior of the human body and to estimate the consequences of exposure to vibration [4]. Matsumoto and Giffin [5] compared the two models and found that the two-degree-of-freedom model is more appropriate. Esat et al. [6] extended the model into three-dimensional and applied the finite element method for head-neck system analysis.

The vibration properties for different loading conditions are estimated. The variety of tissues and muscles of neck are considered. Mortensen et al. [7] improved the head-neck model by increasing the flexion strength by introducing the hyoid muscles. Such musculoskeletal model is a powerful tool for study injury risk, dynamics and kinematics of the system. However, the mathematical model is assumed as a linear one. Better way ofcharacterizing human vibration requires the introduction of the nonlinearity in system description [8]. Namely, measuring results give that the resonance frequency decreases with increasing vibration magnitude due to nonlinearity which is evident in the human body. The human head- neck system is a complex and flexible biomechanical structure which has a continual and a feedback control for minimizing the translation and rotation of the head during the motion [9].

However, based on the relation between the active head restraint position and peak neck motion, it is indicated that the potential protective effects are not fully activated at the time of peak neck motion [10]. For all ofthe previously mentioned analysis it is common that they need the knowledge of the biodynamic parameters. To overcome the difficulties of measuring of biodynamic properties of living human subjects, human vibration models are most frequently constructed by using an inverse dynamic approach [11]. The inverse approach estimates the unknown biodynamic properties of a model using the parameter identification procedures. Data are obtained by measuring of human body response on vibration disturbance [12]. These values are relevant for parameter identification of the dynamic model. Various identification methods for biomechanical models are developed [13], the steepest descent method, simplex and the Levenberg - Marquardt algorithm, predefined MATLAB functions, genetic algorithms, multi-criteria analysis, etc. The methods are very complex and usually the obtained values are not easy to be discussed.

The objective of this study is to give the qualitative analysis of the motion of the head-neck system modeled as a two-degree- of-freedom nonlinear system with harmonic excitation which is transmitting from the body to the head. The proposed model is able to represent a realistic behavior of the relative contraction and extension of the head-neck system. After introduction, in this paper, the mathematical model of the t.d.f system is given. Numerical simulation of the model for various values of excitation parameter is done. Lyapunov spectar and bifurcation diagrams are plotted with the aim to determine the parameters for chaotic motion. In the next section the method for suppressing chaos is discussed. Due to the control with a function with time delay, chaotic motion in the system is eliminated. The paper ends with proposal for stabilizing of the motion of the head and elimination chaos as one of potential causes for injuring.

In Figure 1 the model of the head-neck system is plotted. It is a t.d.f mass-in-mass system. Mass m1 corresponds to the body, while m2 is the lumped mass of head. Connection between masses is viscoelastic: spring and damper model the neck tissues and muscles. As it is already published, in Figure1a the stiffness of the spring is linear, while in Figure 1b the stiffness of the spring is nonlinear. The excitation acts on the mass m1 and the transient force is assumed to be of harmonic type. Mathematical description of the model given in Figure 1b is

Figure 1: Model of the head-neck-body system: a) linear and b) nonlinear model.

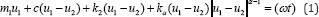
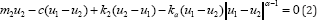
where ϵRe_+ , c is the coefficient of damping, k2 and k_a are coefficients of the linear and nonlinear stiffness, ul and u2 are independent displacement functions, F0 and « are amplitude and frequency of excitation. Introducing the new variable x=u_1-u_2, after some transformation, the relative motion of masses is obtained as

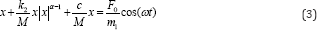
Where 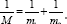The equation (3) is strong nonlinear. To find the closed form solution is impossible. It is the reason that the numerical analysis of the equation is suggested [14].

For the case when the order of nonlinearity is α 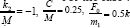and a> = 1, the equation of relative motion is

Figure 2: a)Lyapunov spectrum; b) bifurcation diagram [14].

where k is the excitation parameter. Let us analyse the motion of the system for various values of parameter k. In Figure 2 the Lyapunov spectrum and the bifurcation diagram versus exitation parameter k is plotted. From the Figure 2 it is seen that for k e [1.05,1.39] one of the Lyapunov exponents is positive. For these values of k the motion is chaotic. In Figure 3 the phase plane diagrams and the Poincare maps for certain values of k are considered. From Figure 3a it is seen that the motion is periodical: for k = 0.95 with period 1T, while for k = 1.5 with period 3T. For k = 1.203 in the Poincare map the strange attractor is obtained (Figure 3b). Existence of strane attractor proves the existence of the chaotic motion.

Figure 3: Phase plane diagram and Poincare map for: a) k=0.95 and k=1.5; b) k=1.203 [14].

It is supposed that the chaotic motion in the human body can be suppressed by a type of delayed feedback control which stabilizes the unstable periodic orbits within the strange attractor. To simulate the control procedure a function with time dalay t is considered [15]

c(t ) = k ( x(t -τ) -x(t)), (5)

where K is the constant weight of perturbation. Introducing the control function in the system we obtain

Figure 4: Phase plane diagrams before (grey line) and after (black line) chaos control [14].

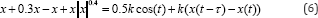
The control procedure depends on the parameters K and τ To stabilize the system with the T-periodic solution we choose τ=T By numerical experiment the value of the weight of the feedback parameter K is selected. Thus, chaos control is achieved with the weight of perturbation parameter K=0.5 and the time delay x=2n. In Figure 4 the phase plane diagrams before and after chaos control are plotted.

In the paper the human head-neck structure as a nonlinear t.d.f mass-in-mass system is modeled. It is concluded that due to nonlinearity some new phenomena in the relative motion of the head to the whole body occur. In addition to periodic steady state relative motion of the head, the chaotic motion, which can cause some damages, may appear. Using the control procedure, by applying the time-delay function, the stabilization of the periodic motion and suppression of the chaotic relative motion is available. The efficiency of procedure strongly depends on parameters of the control function. It is beleived that this conclusion would support the assumption that the head-neck injuring risk depends on the time when the potential protective effects are activated.

1. Panjabi MM, Cholewicki J, Nibu K, Grauer JN, Babat LB, Dvorak J (1998) Mechanism of whiplash injury. Clinical Biomechanics 13(4-5): 239-249.
2. Sarac H, Laporte S, Sandoz B (2017) Evaluation of a passive model to mimic dynamic head/neck movements. Computer Methods in Biomechanics and Biomedical Engineering 20: 191-192.
3. Wei L, Griffin J (1998) Mathematical models for the apparent mass of the seated human body exposed to vertical vibration. Journal of Sound and Vibration 212(5): 855-874.
4. Rutzel S, Hinz B, Wolfel HP (2006) Modal description - A better way of characterizing human vibration behavior. Journal of Sound and Vibration 298(3): 810-823.
5. Matsumoto Y, Griffin MJ (2003) Mathematical models for the apparent mass of standing subjects exposed to vertical whole-body vibration. Journal of Sound and Vibration 260(3): 431-451.
6. Esat V, van Lopik DW, Acar M (2005) Combined multi-body dynamic and FE models of human head and neck. IUTAM Proceedings on Impact Biomechanics: From Fundamental Insights to Applications. Springer: 91-100.
7. Mortensen JD, Vasavada AN, Merryweather AS (2018) The inclusion of hyoid muscles improve moment generating capacity and dynamic simulations in musculoskeletal models of the head and neck. PLoS ONE 13(6): 1-14.
8. Huang Y, Griffin MJ (2009) Nonlinearity in apparent mass and transmissibility of the supine human body during vertical whole-body vibration. Journal of Sound and Vibration 324(1-2): 429-452.
9. Happee R, de Bruijn E, Forbes PA, van der Helm FCT (2017) Dynamic head-neck stabilization and modulation with perturbation bandwidth investigated using a multisegment neuromuscular model. Journal of Biomechanics 58: 203-211.
10. Ivancic PC, Sha D, Panjabi MM (2009) Whiplash injury prevention with active head restraint. Clinical Biomechanics 24(9): 699-707.
11. Dong RG, Welcome DE, McDowell TW, Wu Z (2015) Theoretical foundation, methods, and criteria for calibrating human vibration models using frequency response functions. Journal of Sound and Vibration 356: 195-216.
12. Rakheja S, Dong RG, Patra S, Boileau PE, Marcote P, Warren C (2010) Biodynamics of the human body under whole-body vibration: Synthesis of the reported data. International Journal of Industrial Ergonomics 40(6): 710-732.
13. Srdjevic Z, Cveticanin L (2012) Identifying nonlinear biomechanical models by multicriteria analysis. Journal of Sound and Vibration 331(5): 1207-1216.
14. Cveticanin L (2018) Chaos in oscillators, in Strong Nonlinear Oscillators. Springer: 247-277.
15. Pyragas V, Pyragas K (2006) Delayed feedback control of the Lorenz system: An analytical treatment at a subcritical Hopf bifurcation. Physical Review E - Statistical, Nonlinear and Soft Matter Physics 73(036215): 1-10.