Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
T Moguilnaya*1, A Voloshin2 and A Sher Yshev3
Received: July 25, 2018; Published: August 03, 2018
*Corresponding author: T Moguilnaya, J JSC “SERVET-M”, 115404, 8th Radial street, Moscow, Russia
DOI: 10.26717/BJSTR.2018.07.001525
In this paper, we present a study of stimulated Brillouin scattering (SBS) by E-coli, B.subtilis and coliphages in water. We found the Lamb-like dip in the spectra of SBS in the presence of organisms in water (higher than 1 cells/ml) at excitation by laser radiation with wavelengths 810 and 1017 nm and power 40¬150 mW. The mathematical model of non-linear interaction of the laser radiation with double-stranded DNA, consisted in two antiparallel chains, was designed to explain this phenomenon.
Keywords:SBS; Pathogens; Laser Monitoring; DNA
We developed a new method based on coherent spectroscopy and created an instrument for controlling pathogenic microorganisms in the flow of water [1]. However, that our method allowed only determining the presence of a given microorganism [2]. At the same time, it is of interest to develop an instrument that not only estimates the concentration of the pathogen, but can also be integrated into an automatic line monitoring water condition. It is known that the automatic determination of the concentration of a given microorganism presented a challenge due to complexity of the processes of interaction of the coherent radiation with the DNA structure. Therefore, in order to create such an instrument and automate the process of monitoring and also determine the concentration of the pathogen, it is necessary to create efficient algorithms for processing incoming information. Building a reliable algorithm for recognizing the patterns of spectral distributions requires to carry out not only a statistical processing of spectra, but also a modeling of physical processes of interaction of DNA of the pathogenic organism with the propagating coherent radiation. However, the sufficient theoretical justification for this method has not yet been developed.
For several years, we have been developing the near IR spectra methods for on-line diagnostics of pathogenic organism in aqueous solutions. These techniques are based on non-linear optical phenomena of stimulated luminescence and Brillouin scattering. To this end, we conducted an additional study of stimulated Brillouin scattering (SBS) by solutions of E-coli, B. subtilis and coliphages in water. The mathematical model of non-linear interaction of the laser radiation with double-stranded DNA (consisting in two antiparallel chains) was created to explain the detected phenomena. The theoretical study of the propagation of radiation in DNA structures helped to predict experimental result. We want to predict, what kinds objects can be detected by this method.
We used a specially designed testing bench. The scheme of the experimental setup is shown on (Figure 1). We analyzed about 700 spectra of pathogens, such as Escherichia coli, Shigella flexneri, Bacillus subtilis var. niger and other strains. The bacterial cultures were grown at 37 °С, for 48 h under aerobic conditions on solid nutrient media (agar Hottinger, pH 7.2). For the analysis suspensions of bacterial cell (B. subtilis var. niger and Sh. flexneri) were prepared in 2 mL of 0.9% NaCl with the concentrations 105 and 103 cells/ml. The sensitivity was assessed by using bacterial suspensions of live microorganisms with concentrations 1 × 102 cells/ml, 1 × 103 cells/ml 1 × 104 cells/ml, 1 × 105 cells/ml, 1 × 106 cells/ml, 1 × 107 cells / ml, 1 × 108 cells / ml, and also the suspension of inactivated (30 min; 1000C) E. coli microorganisms with the same concentrations. The specificity was assessed by using the mixtures of E. coli and Sh. flexneri microorganisms in a concentration of 1 × 104 cells/ml, and ratios of 1: 3, 1: 1, and 3: 1; and mixtures E. coli and latex particles in a concentration of 1 × 104 cells/ml, and ratios of 1: 3, 1: 1 and 3: 1.
Figure 1: Experimental installation:1 - Laser source 810 nm, 2 - cuvettes with the sample under evaluation, 3 - spectrum analyzer, 4 - the computer, 5, 6 - optical waveguides.
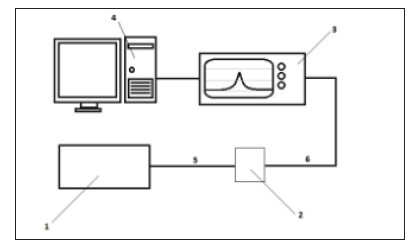
The sensitivity was assessed using bacterial suspensions of live microorganisms with eight concentrations - 1 × 102 cells/ml, 1 × 103 cells/ml 1 × 104 cells/ml, 1 × 105 cells/ml, 1 × 106 cells/ ml, 1 × 107 cells / ml, 1 × 108 cells / ml; and the suspensions of E. coli microorganisms with the same concentrations but inactivated for 30 min at 1000C. The specificity was assessed using the mixes of E coli, and Sh. flexneri microorganisms with the concentration of 1 × 104 cells/ml, and with the ratios, respectively, of 1: 3, 1: 1 and 3: 1. We also used mixes of E. coli and latex particles with the same concentrations and the same respective ratios. The bacteria suspensions were excited with a laser beam having wavelengths of 810 and 1017 nm, and then the forward-scattering spectra were evaluated. The testing bench consisted of the following components: 1- the block of the three of semiconductor laser sources with wavelengths λ1 =1017 nm, λ2 = 810 nm, 2 - the quartz cuvette; λ3 - spectrum analyzer “Agilent” or YOKOGAWA AQ6370C with the spectral resolution 0.05-0.01 nm, equipped with the microcomputer for processing spectra; 4 and 5 - waveguides for the radiation input-output; 6 – the computer equipped with original software for processing spectra.
The laser radiation passed through a waveguide into cuvette with the specimen. In some cases, we used an additional laser with a wavelength λ4= 532 nm. That source enhanced the intensity of luminescence. The radiation that passed through the cuvette and the output waveguide, was analyzed by a spectrum analyzer. Radiation was registered in short-range IR. Experiments were repeated, at least, 40 times for getting statistical significance. Spectral characteristics were measured for a range of concentrations E-coli, from 102 to 109 (cell/ml). The data were saved into a spectra database. The final spectral distributions were transmitted into the computer [3,4], for their processing. Spectral distributions for each concentration were collected for several minutes with the results being averaged in groups of 10. The concentrations of E-coli 10-106 (cell/ml). were studied (Figure 2) represents examples of distributions of the logarithm of the spectral intensity (dbm) for Staphylococcus spectra in water solution: a - concentration of 102z cells / ml; and b - concentration of 105 cells / ml. One can see that at low concentrations of the tested object, only one peak of the Stokes component is formed. When the concentration increased, with subsequent increase in the luminescence intensity, several peaks were formed; both in the Stokes and anti-Stokes regions. They have a dip resembling Lamb dip.
time, for the developed method the difference between the frequencies (wavelengths) of the maximum of the Lorenz component of a laser mode and the maximum of the Lorenz component of a Stokes component was found to be an informative parameter [4]. However, the Stokes component exists in the spectrum no more, than 20 minutes. During this time pathogen DNA obviously will be destroyed. For a practical application, we can use the difference between the frequency maximum of the laser mode and the frequency maximum of the fundamental mode of the bacteria (Figure 2). In (Figure 3) shows the spectral distributions of E-coli combined by the concentrations. All spectra of the same concentration were obtained by examining the same sample at different moments of time, within 10 minutes from the starting its irradiation. The summary base of the spectral distributions was based on 500 spectra. The total number of processed experimental points exceeded 90,000.
Figure 2: Example of distributions of the logarithm of the spectral intensity (dbm) for Staphylococcus spectra in water solution a - concentration of 102cells/ml; b - concentration of 105cells/ml.
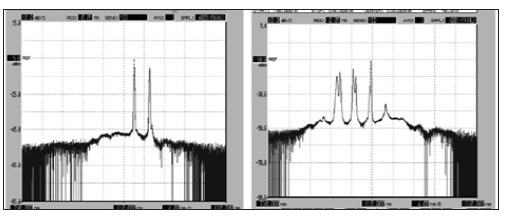
Figure 3: A Spectral distributions of the e-coli solution at a concentration of 102, b-The wavelength of the laser source is 810 nm.
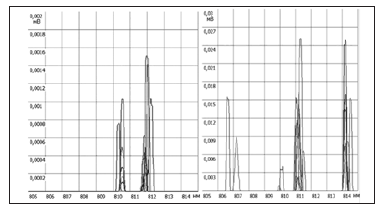
Here is a brief summary of the dynamics of the formation of spectra. Spectra of bacteria, unlike viruses often have several maxima (Figure 2) We found that with an increase in the concentration of the object of the investigation t, the intensity of luminescence also increases, and starting from a certain level several Stokes components can be observed. Among them, there is always a component with the constant difference in wavelength with the maximum intensity of the Stokes component and the wavelength with the maximum intensity laser mode. However, as a rule, only one peak has an intensity maximum at the same frequency in different solutions, such as water or physiological solution. And the position of only one peak depends on the concentration. The logarithm of the intensity at that frequency is a linear function of the concentration up to a level of 105 of cells/ml. Figure 3a & 3b show the distribution of the field at low and high DNA concentrations. In Figure 3a, which corresponds to a concentration of 10, intensity peaks appear at wavelengths of 807.5 nm; 810.4 nm; 811.8 nm. In this case, peaks with a maximum of 810.4 nm correspond to the laser mode. And the Stokes component (811.8 nm) and the anti- Stokes component (807.5 nm) are indicating the presence of the object of investigation. Results of our investigation of dynamics of changes in the intensity of the peaks were given in [3].
From (Figure 3a) it follows that in the case of averaging for low concentrations the gap is formed in the shape of a known Lamb dip. And at the high concentrations, as it is shown in (Figure 3b), the field begins to form as a periodic structure, which leads to a periodic formation of the acoustic field. And, consequently, it leads to the appearance of several Stokes or anti-Stokes components. However, the intensity is not an informative parameter, because it will depend on a power of IR Source. Most of the obtained spectral distributions fit into narrow ranges of wavelengths. That allows one to estimate the probability of belonging of the particular spectral distribution to the set of spectral distributions of pathogenic microorganisms along the wavelengths where the intensity peaks occur, and to apply methods of the pattern recognition theory for the estimation of the concentration. The relationship between the absolute value of the radiation intensity and the concentration is nonlinear. The intensity peaks are not stable in time. From the above, it can be concluded that the intensity is not a reliable informative parameter for the recognition of spectral distributions of pathogenic microorganisms. At the same We found the Lamb-like dip of the spectra of SBS in the presence of organisms in water (higher than 1 cells/ml) at excitation of laser radiation with wavelengths 810 and 1017 nm and power 40 150 mW [5].
The mathematical model of non-linear interaction of the laser radiation with double-stranded DNA, consisting from the two antiparallel chains, was developed to explain this phenomenon. The Stokes wave propagates in the direction opposite to the direction of laser pumping wave. We have two waves with close frequencies, which propagate in opposite directions onto two anti-parallel chains of DNA. The difference between the wavelengths of the maximum of the laser pumping spectrum and the Stokes component is 4-6 nm. We assumed that the increase in the number of Stokes components and the appearance of a dip in the Stokes components are due to the Doppler Effect, which is a result of motion of DNA molecules. At the SBS phenomenon, the Stokes’ and exiting waves, having nearly the same frequencies, propagate in the opposite directions. The electromagnetic field formed in the DNA water solutions leads to the saturation of population density of two kinds of molecules. Ones of them move with a speed +V, and others move with a speed -V [5].
We observed a decrease in the band shape of Stokes components and the appearance of two maxima, which are localized symmetrically with respect to the center of this component similar to Lamp dip, the effect being well-known for gas lasers. According to the above we can assume that waves move to meet each other in a spiral in this structure. In this case, we used the mathematical approximation of “Lamb dipole” to solve this problem. The Lamb dipole is a dipolar vortex structure with a continuous vortex distribution intensity of Stokes components. This dipole moves along a straight line with a constant velocity and without change of form. We solved stationary equation of the Navies-Stokes when there are no viscous effects and the domain is infinite. The results of this study will used to improve sensitivity in the determination of the pathogen concentrations in water.
DNA is a typical periodic rotating nanostructure. We use the results of the investigations carried out in [5,6]. The basic topology of the group and their interaction determine structure of DNA as helicoidal. Moreover, it is traditionally noted that the length of molecules is always significantly larger than their diameter, This the basis for the model representations, where the molecule is described as a deformable string, when its behavior is not associated with a change in its internal structure. There are also two types of forces that stabilize the structure of the double spirals:
a) Hydrogen bonds between the complementary bases, which, following Watson-Crick, are combined into pairs A (adenine) -T (thymine) and G (guanine) -C (cytosine), bonded, respectively, by two and three hydrogen bonds.
b) Covalent bonds, by which the bases are connected along the DNA strand. It is important to note that the hydrogen bonds are much weaker as compared to the bonds along the chain.
Aromatic bases have a Van Der Waals scale of 3.4 Ǻ and, consequently, a partial base stacking effect is observed. Persistent lengths of rotary and flexural modes represent the natural scales for thermal fluctuations (approximately 15-20 h). DNA is a fairly rigid polymer due to effect of stretching of the corresponding pairs of amino acids by chemical and hydrogen bonds. Thermal persistent DNA lengths for bending and rotation are, respectively, 150 bp (50 nm) and 220 bp (75 nm).
c) At spatial scales of thousands of base pairs (~0.5 μm), DNA is in vivo organized into topologically independent loops. DNA molecules with sizes of 2-10 kbp are “bound” sets. The main part of the genes (prokariotic cells) is organized as single closed DNA with dimensions of ~2 nm. We observed several peaks with an increase in the concentration of the pathogen in the solution. We assumed that the main contribution to luminescence is produced by radiation passing through the base of the nucleic acid. This allowed us to simplify the mathematical model.
The effective field method is often used in theoretical models in the form of an auxiliary (real or presumed) action to describe complex inter-particle interactions that are impossible (or difficult) to describe in detail, or when the nature of these interactions is unknown. In our consideration, the definition of the “effective field” is the total field formed as a result of the interaction between the auxiliary electromagnetic and elastic fields. This field is radiating as a rotating source with the velocity of the spirals moving along the fixed DNA structure. The source of this field is called the “The Lamb dipole” [7]. We observed in our experiments the appearance of Stokes components after a short time after the start of irradiation. We simulate the process of interaction of the fields in DNA starting from the moment of formation of the Stokes components. Here is the structure we have used in our model. Let us consider in detail the model of the radiation source. The Lamb dipole is a dipolar vortex structure with a continuous vorticity distribution within a circular region. This dipole moves along a straight line with a constant velocity and without change of form.
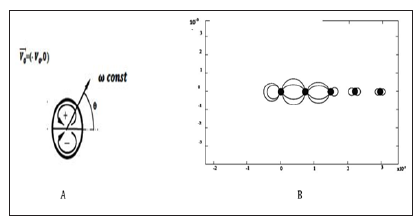
Dipole is a stationary solution of the two-dimensional vorticity equation (Navier-Stokes equation) when there are no viscous effects and the domain is infinite. When viscous effects are considerable, the vorticity is spread over a larger area, and the dipole decreases in strength, so that the velocity also decreases in the course of time. The motion remains along a straight line though. In the case of the finite domain, the velocity of the dipole is smaller than in the infinite domain. The Lamb dipole has a continuous vorticity distribution within a circle of radius a. Inside this circle there is a linear relationship between the vorticity omega (ω) and the stream function psi, (ψ) namely: omega= k2psi; where k is a constant given by k=3.83. Outside this circle there is no vorticity: omega ω=0. The flow outside the dipole is a potential flow: a two-dimensional flow around a circular cylinder placed in a flow field with a uniform velocity V0, (Figure 4a). As indicated in the figure above, one half of the dipole has positive vorticity, whereas the other half has negative vorticity. The total circulation, that is the ‘sum’ of all vorticity, is equal to zero [7]. In this case, the equations for the propagation of the electric field for a Gaussian beam in a vector form appear for our model in the following manner in space
Figure 4: (A, B) Explanation of the geometric model: A) the Dipole Lamb model Θ-spiral turn (360) [5] B) The total field from all the rods is averaged when calculating the intensity.
Where,
the frequency shift
μ-1r the magnetic susceptibility of the medium; E - electric field strength; k, kz -
propagation constants; ∈r,∈0 - dielectric constants of the medium and vacuum; ω - the plasma
frequency; j- is the electric field strength,
n – refractive index and λ - pump wavelength.
In the opposite direction, the gain resulting from the energy of the hypersonic wave is
given by the expression  gain due to interaction
with a hypersonic wave.
gain due to interaction
with a hypersonic wave.
Where ΔνΒ- spectrum width at half-height ρ0 - material density;λp-pump
wavelength; p 12 longitudinal acoustooptical coefficient for water [4]. The boundary conditions have the form of approximate expressions describing the Dipole
Lamb:
Figure 5: (A, B) A)- distribution of the intensity of the electric field of chain at low concentrations of E-coli 10-2 cells / ml, B)-Distribution of the electric field in a system at high concentrations of E-coli 10-5 cells / ml.
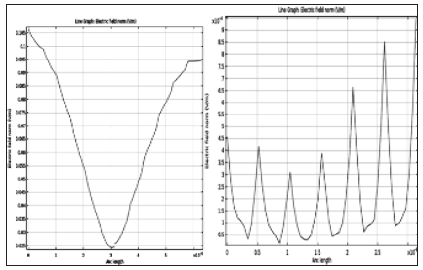
where: V1, V2 V 3 - are the linear projections of the rotation speed; u - is the average linear velocity of flow from the flow in the Z direction; EZ - is the source potential F -is the Lorentz force. F- the electrostatic potential of the molecule. For calculation, the electrostatic virus of the tobacco mosaic was taken [8]. The total field from all the rods was averaged when calculating the intensity. The data for the calculation were taken from the publications [5,6]. The solution to this problem was carried out in the COMSOL program. In Figure 5 shows distribution of the intensity of the electric field of DNA chain at low concentrations of E-coli (10-2 cells / ml) in solution and shows distribution of the electric field in a system at high concentrations of E-coli 10-5 cells /ml. An analysis of the presented curves shows that the superimposed electric field is a periodic structure, with each of its maxima diffracting at the radiation densities; and it can be causing not one, but several Stokes components. Since the luminescence intensity increases with increasing of the concentration, the number of closely spaced maxima increases. The analysis of that distribution will be the basis of the algorithm for determining concentrations in the device for controlling pathogens directly in the water.
We found that with an increase in the concentration of the investigated pathogen, the intensity of luminescence also increased. And after reaching a certain level of intensity we began observing several Stokes components. Among them, there was always a component, in which the difference in wavelengths of the maximum intensity of the Stokes component and the maximum intensity laser mode was independent from the concentration. However, as a rule, only one peak has an intensity maximum at the same frequency in different solutions, such as water or physiological solution. We found that, regardless of the concentration of the pathogenic organism, most of the obtained spectral distributions fit into the narrow ranges of wavelengths. That enable us to estimate the probability of belonging of a specific spectral distribution to the set of spectral distributions of pathogenic microorganisms along their wavelengths, where the intensity peaks are observed, and to apply the methods of the theory of pattern recognition for the estimation of the concentration. This will create the base for the design of the efficient recognition system for an automated system applicable to the control of pathogenic microorganisms. We developed a qualitative model of radiation propagation through DNA, which demonstrated that the superimposed electric field is a periodic structure, with each of its maxima diffracting at the radiation densities; and it can be causing not one, but several Stokes components. Since the luminescence intensity increases with increasing of the concentration, the number of closely spaced maxima increases. The analysis of that distribution will be the basis of the algorithm for determining concentrations in the device for controlling pathogens directly in the water.


