Consciousness as Topologic Information Integrator Volume 7 - Issue 1

Robert Skopec*

• Researcher-Analyst, Slovakia

Received: July 14, 2018;   Published: July 23, 2018

*Corresponding author: Robert Skopec, Analyst-Researcher, Dubnik, Slovakia

DOI: 10.26717/BJSTR.2018.07.001456

Abstract PDF

Summarizing we can describe the following logical chain. Spontaneous appearance of “living” states in physico-chemical systems is impossible in sense that it is extremely improbable. However, with the help of the biological systems this process constantly occurs. Hence, the consciousness make re-normalization of probabilities of states and it is topologically determined by higher structural level (omnicausal determinance). Such omnicausal re-normalization of probabilities, as was mentioned although not evidently by many authors, is a characteristic for all levels of the biological hierarchy from a neuron up to the biosphere.

Abbreviations: SOM: Self-Organizing Map, SNA: Strange Nonchaotic Attractor, EEG: Electro Encephalo Gram, EM: Expectation Maximization, MDP: Markov decision problem

As Brain phenomena, the consciousness can be studied as a mathematical structure, representing integration of neurobiological information. The higher mental processes all correspond to well-defined but, at present, poorly understood information processing functions that are carried out by physical systems, our brains [1]. Consciousness is generated by certain parts of the brain, including the thalamocortical system. According to G. Tononi [2], consciousness corresponds to the capacity of a system to integrate information. He proposed to measure the quantity of consciousness availed to a system as the Φ value of a complex elements, representing the amount of effective information that can be integrated through the informational weakest link of a subset of elements. A complex is a subset of elements with 0Φ>, that is not part of a subset of higher Φ. The quality of consciousness is determined by the informational relationships among the elements of the complex, which are specified by the values of the effective information among them [3]. Each particular conscious experienece is specified by the value of the variables mediating informational interactions [4] among the element of the complex. The neural processes underlying consciousness can influence or be influenced by neural processes that remain unconscious. Information is classically defined as reduction of the uncertainty, measured by the entropy function [5], which is the weighted sum of the logarithm of probability (p) of alternatives outcomes (i):

To measure the information integration capacity of a subset S we search the bipartition of S for which effective information EI(A↔B)reaches the informational weakest link, should be normalized by H^max(A↔B)=min{H^max(A),H^max(B)}, the maximum information capacity for each bipartition. The information integration for subset S is ()SΦ which is the normalized value of value ()EIAB↔for the minimum information bipartition:

The complex with the maximum value of Φ(S) is the main complex. A large complex of high Φ can be constructed by joining smaller complexes through reciprocal connections. The physical substrate of our consciousness is undergo a refinement and rearrangement in connections patterns among neurons of the appropriate parts of the thalamocortical system. Each conscious state represents a different point in the multidimensional qualia space defined by the effective information matrix of the complex. The flow of information matrix (mediating informational interactions) can be thought as a trajectory of points in qualia space. Consciousness in this way corresponds to the capacity to integrate information. The neural substrate of consciousness is a distributed [6] thalamocortical network.

The organization of the thalamocortical system emphasize at once both functional specialization and functional integration. Other brain regions with comparable numbers of neurons, such a s the cerebellum, which receives mapped inputs from the environment, and controls several outputs, or some sub-conscious centers, must not contribute to conscious experience. A selective measure of neural complexity can be sensitive to neural dynamics underlying rich adaptive behavior. It may be understood in terms of adaptation to complexity in the unpredictable and highly variable environment. The evaluation of the fitness of each neural network using stochastic rank-based selection to replace low fitness networks with mutated versions of high-fitness networks.The mutation of a network involved randomly rewiring one connection, also modifying the strength of each connection with given probability [7]. The fitness of the network with the fitness of each trial Φ is given:

where t_j denotes the number of time-steps for which the target was fixated, t_tot the total number of time-steps in the trial (in given case 600), and d the mean offset between the positions H and G for the trial. The neural complexity C(X ) of a system X means that in a small subsets of the system show high statistical independence, but the large subsets show low statistical independence [8]. Such systems reflects an even balance [9] between integration and segregation in the dynamics of a network. As larger and larger subsets of elements are considered, they become increasingly integrated. Integration I (X ) captures the overall degree to which the dynamics of a system deviate from statistical independence. The entropy H(X ) characterizes the overall statistical independence of the elements of X . The covariances of the elements of X is COV (X) can be derived analytically from the corresponding connectivity matrix c_ij(X)

Where T indicates matrix response. The resulting values of C(X ) , I (X ) , H(X ) , are independent of behavioral context. Basic concepts of consciousness, neurons, neuronal space, local spheres of neuronal influence, cellular neighbourhoods, are parts of the topological macroinstruction on how to transform an input image into an output image, under the flow diagram of the algorithm [10]. The mixture of analog and digital components are specific for the neural information processing in living organism (for instance neurons in the Lateral Geniculate Nucleus response to an optimally oriented bar of certain length) and the visual cortex function is orientation selectivity. Also feedback coupling leads brain systems towards a conscious synchronized state [11] with a vector of variable errors which tend toward zero as the gain increases. The limit value of the interaction term in consciousness will converge towards the difference between the guiding system evaluated on its own dynamics minus the guided system (motor cortex) evaluated on the guiding dynamics. But synchronising different systems is not cost free. The cost of synchronization is a measure of the magnitude of the interaction term [12].

If the systems are flexible enough as to capable of adapting their structures, the slave system may start a process of adaptation in order to reduce the synchronization cost. The result could be complete synchronization at zero cost, it means identical synchronization. This is particularly possible in biological systems, for instance, groups of similar neurons, that might need to synchronize their behavior in an extended region [13]. In communication systems using chaotic waveforms, including the human brain, we can consider n-dimensional chaotic oscillator in the form:

where f : Rn → R and g : Rn → Rn−1 are continuous functions. The analog information signal s(t)∈ R is injected into the oscillator: x = f (x, y) + cs(t) , y = g(x, y) , where c > 0 is a scaling constant. In the communication scheme x(t) is the scalar transmitted signal. At the receiver we have a synchronous subsystem y = g(x, y) . A complex nonlinear filter with a robust algorithm could neurochemically recover the information signal described as:

where the gain k > 0 is a constant, and s(t) represents the recovered signal through the demodulation of memory [14]. The neuronal avalanches are a generic property of cortical networks, and represents a mode of activity differing from oscillatory, synchronized, or wave-like network states. In the critical state [15], the network may satisfy the competing demands of information transmission and network stability. Neuronal activity is a kind of neuronal avalanche in which activity propagates as individual neuron trigger action potential firing in subsequent neurons. The probability distribution of avalanche sizes revealed a simple, linear relationship in log-log coordinates. Linear relationship demonstrated the existence of a power law P(n) nα , where n is the size of an avalanche, P(n) is the probability of observing an avalanche of size n, and α is the exponent of power law, giving the slope of the relationship. The critical state, especially under conditions of sparse network connectivity, as it is in neocortex, would maximize the information transmission. The propagation of synchronized action potentials in the form of neuronal avalanches through the network, and the power law of -3/2 provides the statistical framework, for transmitting information through the cortical network in form of locally synchronized action potential volleys.

The concept of self-organized criticality states [16], that many systems of interconnected, non-linear elements evolve over time into a critical state, in which avalanche is scale-free and can be characterized by a power law. Processing networks in sensory cortex carry out transformations on their inputs so as to create outputs relevant for perception and action. The transformations are characteristic of an area, rely on discrete local circuits, computed both dynamically and invariantly, despite variations in functional architecture within the area. The computation of feature selective responses, such as orientation selectivity in primary visual cortex (V1), involves the integration of excitatory and inhibitory inputs, from variety of sources to produce responses sharply tuned for the orientation of visual stimuli [17], that are also influenced adaptively by history of stimulation. The composition of the local circuit varies systematically across the orientation preference map in V1. The interplay between excitation and inhibition is an essential mechanism for stabilizing and shaping neural activity. Computational models of cellular and network behavior support the conclusion [18] that the cortical network operates in a recurrent rather than a purely feed-forvard mode. The simple rules of spatial integration of excitation and inhibition can explain sharp orientation tuning at all locations of the orientation map. This functional balance derives from spatially isotropic local conectivity of both excitatory and inhibitory neurons [19].

The self-organizing map (SOM) is another tool of consciousness for understanding high-dimensional data. SOM projection is used for mapping high-dimensional data onto the two-dimensional grid [20] structure with a growing self-organizing mechanism. A mapping proces of real world data from the high-dimensional input space transform it to a low-dimensional output space. This mapping provides better insight into the data structure and clustering tendency. In the SOM the input data is mapped to a lowdimensional discreet grid of neurons, which is usually rectangular or hexagonal shaped. All neurones within a certain neighbourhood are updated instead of a single unit according to

where h (t) ci is the neighbourhood function (NF), which is centered on the best match neuron, and decreasing monotonically with the time. A typical smooth neighborhood function could be the Gaussian,

where α (t) is the learning function, σ (t) is the width of the Gaussian kernel and||r _c-r_i||² is the distance between the winning neuron and the neuron i with r_c and r_i representing the twodimensional positions of neurons c and i on the SOM grid. The learning process consist of winner selection, and adaptation.

The selection and adaptation in brain is based on the conscious predictive metalearning system of neuromodulator circuits within the circuits of basal ganglia, which has been suggested [21] as major locus of reinforcement learning. For prediction functions are important also the connections of prefrontal cortex, thalamus, cerebellum, etc. In a computational theory on the roles of the ascending neuromodulatory systems, they are mediating the global signals (metainstructions) regulating the distributed learning mechanism in the brain. Dopamine represents the global learning signal for prediction of rewards and reinforcement of actions [22]. The reinforcement learning in this computational framework is for an agent to take an action in response to the state of environment to be acquired reward maximised in a long run [23].

A basic algorithm of reinforcement learning could be considered a Markov decision problem (MDP) assuming a discrete state, action and time. The agent observes the state s(t)∈(s₁....s_n) ,takes action a(t)∈(a₁....a_n) according to its policy, given either deterministically as a = G(s) , or stochastically P(a s) . In response to the agent´s action a(t) , the state of environment changes either deterministically as s(t) = F(s(t),a(t)) , or stochastically according to a Markov transition matrix P(s(t +1) s(t) , a(t) for each action a(t) . The reward r(t +1)∈R is deterministically r(t +1) = R(s(t), a(t)) , or stochastically P r(t +1) |s(t), a(t)) . In this setup, the goal of reinforcement learning is to find an optimal policy maximising the expected sum of future rewards. The architecture for reinforcement learning is the actor-critic, consisting of two parts:

The critic (prefrontal cortex, orbitofrontal cortex, thalamus) learns to predict future rewards in the form of a state value function V (s) for the current policy, The actor (motor cortex) improves the policy P(a| s) ) in reference to the future reward predicted by the critic. The actor and the critic learn either alternately, or concurrently. The synaptic weights between two excitatory units are assumed to be modifiable according to a reward-modulated Hebbian rule Δw^{post, pre} =ε RS ^pre (2s^post −1) , where R is reward signal provided after each network response (R = +1, correct, R = -1, incorrect), pre is the presynaptic unit and post the postsynaptic unit [24]. The reward signal R influences the stability of workspace activity through a short-term depression or potentiation of synaptic weights: Δw^{post, pre} = 0.2(1− w´ ^{post, pre} ) , where w´ is a shortterm multiplier on the excitatory synaptic weight from unit pre to unit post. A type of complex behavior occurring in non-chaotic conscious system is strange nonchaotic attractor (SNA), which can be applicated also in neural information model. The model of a globally coupled neural network consist of N analog neurons {S (t)} i , i = 1,.., N , with − 1 ≤ S_i ≤1 ,where every neuron i S is connected to all others neurons j S by random couplings {J_ij} . The paralell dynamics are used for up-dating of the neurons:

The sigmoidal function which is a typical information transfer function in neural models is used g(x) = tan(α x) ,with α > 0 . The internal field i h of the neuron i S is given by

with ξ_i(t) is the external signal. Usually, the external stimulus affects part of the neural networks [25]. Therefore, assuming that only the first M(M ≤ N) neurons are stimulated by input signal:

The assymetric coupling. SNAs may be observed in real neural systems, particularly with complex biological signals such those seen in epilepsy, and in the electroencephalogram (EEG). The EEG pattern is known as activated because cortical neurons being depolarized and close to their firing threshold, are ready to respond to incoming inputs.

The Information Changing Probability

In Akimov´s Torsion Field theory [26], the longitudal and transverse spin polarisations of phytons throughout space clearly affect its isotropy. In a short way, at a sub-quantum level (of neurons and synapses), they can upset precise mathematical laws by affecting the probability of conscious events. Let x be a vector of observed variables, z be a vector of latent variables, and θ be the model parameters. Let y = (x, z) be a vector of all variables in the model. If y were completely observed we could apply standard maximum likelihood estimation to obtain: argmax log P( y ) θ θ = θ . The z is unobserved, y becomes a random variable and there must be apply the Expectation Maximization (EM) algorithm [27].

For more complex models, the free energy approach leads to more flexible model fitting. The standard EM is equivalent to performing coordinate ascent on the energy function

The q-distribution may be the exact posterior over z or an approximation. The free energy F[q,θ ] is related to Kullback-Liebler divergence between the q-distribution q(z x) and the true posterior p(z x) as follows: log P(x, z θ ) = F [q,θ ]+ D(q(z x) p(z x)) . The Kullback-Liebler divergence is a measure of the difference between probability distributions. If this zero of the distributions are equal, and positive otherwise, thus the free energy F[q,θ ] is a lower bound on the complete data log likelihood. The EM algorithm can be expressed as:

Both the E-Step and the M-Step maximize the same objective function F[q,θ ].

The local maximum of the free energy will only correspond to a local maximum of the expected complete log likelihood when q is a true maximizer of F[q,θ ]. Further, Fourier-like transformations store information of the sensory modalities [28] in the spectral (or frequency) domain. The sensory stimulus is spread out (distributed) over a region of the brain. In the case of vision would be the particular cortical cells respond to the spatial frequencies of the visual stimulus. The dendritic processes function to take a “spectral“ transformation of the „episodes of perception“. This transformed spectral information is stored distributed over large numbers of neurons. When the episode is remembered, an inverse transformation occurs that is also result of dendritic processes. The processes of transformation give the conscious awareness. The main computational event of neurons is the polarizations and hyper-polarizations at the dendritic membranes of neurons. These dendritic processes effectively take close to a Fourier transform. Mathematically a Fourier transform converts a function of time f(t) into a function of frequency F (jw), where the j indicates a complex function of frequency. The Fourier transform can convert a signal from the time domain to the frequency domain. A Fourier transform could be used also to convert from spatial location domain (the coordinates in space) to a frequency domain. The mathematics of the Fourier transform is independent of what the data sets represent. The Fourier transform and inverse Fourier transform are:

Mathematically the two-dimensional spatial Fourier transform is:

and the inverse transform is:

where x and y are spatial coordinates, and a and b are horizontal and vertical frequencies. For instance, central connections of the visual system are specific. Separate regions of the retina project to the lateral geniculate nucleus in the thalamus, in a such a way that a complete visual field for each eye is represented in the nucleus. Different cell types in the retina project to the different targets in the brain stem. Each geniculate axon terminates in the visual cortex, primarily in layer 4. The cells in each layer have their own patterns of connections with other subcortical regions. Cells in the visual cortex are arranged into orientation-specific columns [29], ocular dominance columns, and blobs. Neurons have horizontal connections. Information flows both between the layers and horizontally through each layer. The columnar units function as elementary computational modules. Each group of cells acts as a dedicated circuit to process an input and send it on. The cortical cells are sensitive to higher harmonic components of the Fourier spectrum. These cortical cells are acting like spatial-frequency filters (and not as edge and bar detectors). The higher spectral harmonics of the square-wave grating are at the same orientation as the fundamental frequency, but the higher harmonics of the checkerboard are at other orientations.

The cortical cells exhibits sufficiently narrow spatial tuning, it could potentially respond separately to the fundamental and third harmonics of patterns. An isolated system can itself be divided into a subsystem that is open to energy and information flow, and the subsystem´s environment (Tononi´s „larger complex“). The whole combined isolated system still obeys the second law of thermodynamics, but i tis possible that the subsystem (Tononi´s „smaller complex“) can experience a decrease of entropy at the expense of it´s environment. The entropy increase in the „subsystem environment“ is guarantied by the second law, to more than offset the entropy decrease in the Tononi´s „main complex“ subsystem. The subsystem can only be maintained away from equilibrium as long as there is usable energy in it´s environment. When the environmental energy is maximised (no usable energy), the sub-system is guaranteed to itself proceed to equilibrium. There is a special class of such subsystems, where their organization comes exclusively from processes whiten the sub-systems boundaries. It´s the class of subsystems labelled by I. Prigogine as „dissipative structures“ [30,31].

If we propose that the brain is a ”dissipative structure“, the Boltzmann formulation the principle of the least action leads to a space-time equilibrium state of least energy. The principle of least action [32] describes as leading to maximizing the amount of information and minimizing the entropy. The Fourier coeffients are stored as the micro process of polarisations and depolarisations, occurring in the dendritic networks. The information in its spectral holographic domain is distributed over an area of the brain cells by the polarisation of the various synaptic junctions in the dendritic structures. Correlations and associations can be achieved by other parts of the brain projecting to the same cells. Conscious awareness and memory is the byproduct of the transformation back again from the spectral domain back to the image domain. The receiver is not necessary view the result of the transformation from spectral holographic to image. The conscious experience is concurrent with the brain performing these Fourier transformations simultaneously correlated a perception with other stored perceptions. Conscious experience is based on topological self-correlation (of endomorphisms), and occurs in the dendritic structures by the summation of the polarizations (and depolarizations) in the dendritic networks.

We hyphotesized that a new information could change a probabilities of the neural integration process in consciousness. The most important difference of omnicausal information systems from particausal ones is the change of the entropy sign. In particausal systems entropy on the definition of J von Neumann, corresponds to the “amount of (microscopic) information that is missing in the (macroscopic) description” [33]. But in omnicausal systems macrostate, as it will be stated below, is richer with information than any single microstate. Therefore, at transition from micro- to macro-level, the information is not lost but acquired, which results in negative entropy value in such systems, as it was shown before [34]. Two questions arise here at once. First, in what way can macro-state of the molecular ensemble determine its microstates and, second, by what is this macro-state as information richer of each specific micro-state?

Topological relations between consciousness and the environment A complete description of any microstate is its state function (y-function), which modulus square is interpreted as probability density. It presents itself the result of interaction of y-functions of single particles.

Therefore, any rather specific microstate providing the realization of rather improbable macro-state corresponds to a special type of y-function. It is possible to abruptly increase the probability of such macro-state only by re-normalization of probabilities both microstates which are supposed to be equally probable by the classic theory and the states of single particles (which is finally the same). Thus, living macrostate of the biological system provides the realization of the corresponding microstates by means of re-normalization of probabilities as a result of which the circle of possible microstates and, hence, macro-states abruptly narrows, its mode can shift to the “tail” of the distribution. Such an effect can arise as a result of multiple interactions of the initial (a priori) function of probability distribution for all possible microstates which in complicated biological systems are not equally probable, and the probability filter by means of which macro-state performs omnicausal determinance. Bayes formula can be used here as a mathematical model:

where: p(μ / y) is the distribution function of the living state of the ensemble μ as a result of the probability filter effect, k is the constant necessary from the conditions of normalizing, p(μ ) is a priori distribution function of the ensemble μ , p(y /μ ) is the distribution function disclosing what kind of states of the ensemble μ the probability filter y selects as living ones. For single particles (elements) similar re-normalization is expressed in the decrease to zero of the probabilities of the number of possible directions and speeds of motions. Is the approach of Bayes in all these cases only a suitable mathematical model or does it reflect the essence of renormalization of probabilities process? The first alternative makes the postulate of the unknown types of interaction in biological systems because the interaction known in physics does not seem to fit here. The problem in this case is similar to the one of hidden parameters in quantum mechanics [35]. The second alternative leads to the idea of immediate interaction of y-function of macrostate (let’s name it ω-function) with y-function of micro-state. The notion of w-function has the content only when this ω-function is marked in the macro-world.

Otherwise w ≡ψ . And here we obtain the answer to the second of the set questions above. Possessing time “thickness”, alive macro-state is described by a certain succession of certain and in a certain order replacing each other’s micro-states. It in this way is information richer than any single of them. Moreover, microstates composing biological present are not an alternative. To realize living macrostate, the realization of each of them is necessary in a certain succession. Therefore, by calculating statistical weight of such a state (its logarithm due to Boltzmann equation is equal to the entropy with the accuracy up to a constant) we must not sum up the probabilities of alternative microstates, but multiply conditional probabilities of all succession microstates, composing the “thickness” of present for the given living macrostate. This multiplication results in the statistical weight value less than one and, hence, to the negative value of entropy [36]. For such an actually negative entropy N.Kobozev suggested the name “antientropy”, in contrast to negentropy, which is as a rule explained as a negative increment of positive entropy [37].

Such re-normalization is a constant outer interference (topological neighborhood function), namely, from macro-state side having its own plot, image, plan, into the natural dynamics of microstates. And in this case the element of “miracle”, i.e., discrepancy of the observed processes at the microlevel for the second law of thermodynamics, and uncertainty of future to past, is introduced into the natural dynamics. The measure of this “miracle” element is anti-entropy, and ω-ψ-interaction (re-normalization of probabilities) is the mechanism of anti-entropy origination. The equation of motion for the Wigner distribution W(x, p) is plotted as a function of x and p of a particle coupled to an environment:

(Liouville Equation) (Friction) (Decoherence)

where V is the renormalized potential. The Wigner distribution can be regarded as more complex than classical probability distribution in phase space because it has also negative contributions. The possible quantum aspects of consciousness [38] can be interpreted as a canonical method for solving pattern recognition problems. It relates pattern recognition to the Wigner- Moyal formulation of quantum theory interpretation as a theory of pattern recognition. In a generalization of the Wigner - Moyal phase space gives the physical dimensions as the Weyl quantization of a complete holographic representation of the surface. He replaces the classical variable of position within an electromagnetic field with ordinary creation and annihilation operators. It shows that representing a Riemann surface holographically amounts to a pedestrian version of a mathematically elegant characterization of a Riemann surface in terms of its Jacoby variety and associated theta functions. This representation is equivalent to using the well known generalized coherent states for an SU(n) Lie algebra. This is the formalism employed in [39] to handle the formation of invariances that describe entities and objects.

These formulations are based on quantum-like wavelets, Gabor [40] and Wigner [41] phase spaces. Whether these particular formulations will be found to be the most accurate is not the issue: the fundamental connecting link between mathematics and neurobiology is the pattern recognition of the human brain [42].

The Influence Functional

The Influence Functional is defined as

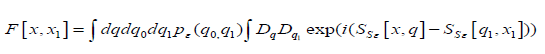where ε p is the initial state of the environment and S_Sε[q,x] is the action of the environment (including interaction term with the system). If there is no interaction (or if two systems trajectories are the same, i. e. x = 1 x ), then the influence functional is equal to one. [ ] 1 F x, x is the so-called influence functional [43]. This functional is responsible for carrying all the effects produced by the environment on the evolution of the conscious system. The energy eigenstates are also selected by the environment. The decoherence in eigen basis can be established ε Π is a momentum operator (as the environment operator acts on the environment as a translation generator), and the initial state of the environment is a coherent vacuum state, the evolution turns out to be such 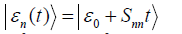, where 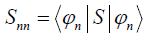. Therefore the overlap between the two states that correlate with different energy eigenstates can be 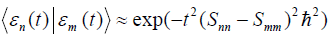. Consequently in this case, there is einselection of energy eigenstates (superpositions of energy eigenstates are degraded while pure energy eigenstates are not affected). For this reason, pointer states are energy eigenstates.

Decoherence Functional

The decoherence functional is defined in terms of which the decoherence process determines the relative „fitness“of all possible superpositions that exist in Hilbert space [44]. The resulting „natural selection“ is responsible for the emergence of classical reality. In the GW its consequence is known as environment-induced super selection, or einselection [45]. In a quantum chaotic system weakly coupled to the environment, the process of decoherence will compete with the tendency for coherent delocalization, which occurs on the characteristic timescale given by the Lyapunov exponent λ . Exponential instability would spread the wave packet to the paradoxical size, but monitoring by the environment will attempt to limit its coherent extent by smoothing out interference fringes. The two process shall reach status quo when their rates are comparable:

Because the decoherence rate depends on δ x , this equation can be solved for the critical, steady state coherence length, which yields 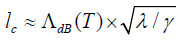. All of the systems that are in principle quantum but sufficiently macroscopic will be forced to behave with classical mechanics as a result of the environment-induced super selection. This will be l_c << x , because c l is a measure of the resolution of „measurements“ carried out by the environment. The basis-dependent direction of the information flow in a quantum c-not (or in premeasurrement) is a direct consequence of complementarity. It can be summed up by stating that although the information about the observable with the eigenstates { 0 , 1 } travels from the measured system to the apparatus, in the complementary {| + − }| − }basis it seems to be the apparatus that is being measured by the system. This observation also clarifies the sense in which phases are inevitably disturbed: in measurements. They are not really destroyed, but, rather, as the apparatus measures a certain observable of the system, the system „measures“ the phases between the possible outcome states of the apparatus.

These phases in a macroscopic apparatus coupled to the environment are fluctuating rapidly and uncontrollably, thus leading to the destruction of phase coherence. However, even if this consequence of decoherence were somehow prevented (by perfectly isolating the apparatus pointer from the environment), preexisting phases between the outcome states of the apparatus would have to be known while, simultaneously, A is in 0 A , the „ready-tomeasure- state“ [46]. Probably P.W. Anderson’s “generalized phase rigidity” of emergent complexity could give an immunity against environmental decoherence. Concerning consciousness Akimov [32] postulates that the two photons spin-polarise the physical vacuum by their motion and leave spin-polarised tracks along their trajectories [47]. These tracks where the phytons are pulled together in aligment persist as a communication channel between the outward flying photons. Variation of the polarisation angle of a photon transmit a torsion disturbance to the other via this spin polarised channel.

Torsion fileds theory suggest, that the laws of probability (chance) selections might be interfered by the existence of spin clusters in the vacuum state. For example, the Hydrogen atom could easily accomodate about 2000 phytons. Their combined spin polarisation would produce an effect akin to gravity. Atoms are the information transducers, where spin polarisation is concerned. It is possible to signal by spin in biological systems. The torsion field responds to shapes, spin is sensitive to symmetry, spin may cause a shaped molecules to fit better into a receptor, topology responds to torsion. One perceives vortices being generated, linking up and imprinting at certain localities. A metabolical process in a neuron goes through generation of electrical potential along a neuron. Torsion fields transmit information in in the form of pulses (avalanches) , which would be spread out far more than digital information sent as electromagnetic waves. The torsion field has no wave structure of peaks (spikes) and throughs, not even energy packets. The spin of one phyton, aligned transversally, connects with its neighbour and instantly trough space to the destination. The phytons have no mass and are already spinning randomly.

In biological systems, the shaped molecules emitted by glands, can absorb torsion field spin in a slow build-up, similar to the build-up of potential in a neuron. The emitted neuro-transmitters are drawn towards receptor sites and when they lock in place, the molecular spin of the transmitter is suddenly stopped. The synapses in human brain creates powerful pulses, avalanches of spin polarisation which collectively affect quantum states in the vicinity of the brain. Hereby pullses of transverse spin can be transmitted as information (by ionised particles). The termination of spin polarisation puts kinks in the Phyton states, and these kinks form the way, in which information is stored and transmitted. They establish a hologram of intention in space, projecting a picture or a feeling. Topology is used as information amplifier for torsion fields, and message hangs together as a Gestalt pattern. The chance of correct orientation, may be a determining factor in synaptic switching. The probability is opening the door to the influence of torsion fields and spin orientation. For example, the effect of weak magnetic fields upon the pineal glands (melatonin synthesis, circadian rythm), or the magnetic actions coupled with spin, induced in ions by magnetic fields, etc. The spin induced by torsion fields introduces a new probabilistic factor into the action of the neural system of the consciousness.

The torsion is a subtler type of influence, motivated by information, when alter the way chance and probability operate. It could make an unlikely event happen, an enduring influence propagated almost instantly. This fine structure within a particular signal is called spin – spin coupling, the magnitude of separation between the peaks in a multiplet is called the spin – spin coupling constant, denoted by symbol J, and its values are given in Hertz. During rotation about C – C bonds, the value of J for a given Hydrogen depends upon the dihedral angle, the magnetic moments of proton affects the spins of the electrons, forming the covalent C – H bond. This change in turn affects the spins of the C – C electron pair, passed on the electron pair in the adjacent C – H bond. The spinning effect of one photon is passed through the covalent bonds to the other proton. These effects depends only on the structure and geometry of the molecule, they are independent of the strength of the applied field. The spin system (Tononi´s „larger subset“, and “smaller subset“ of a complex) is describing groups of nuclei, that are spin – spin coupled, but not with any nuclei outside the spin system.

It is not necessary all the nuclei within the spin system to be coupled to the all the another nuclei. The molecule may consist of two or more parts insulated from each other and giving rise to two or more spin systems. The first order spin frequencies (values of J) for typical carbon bonded molecules range from 0 to 60 Hz, at NMR frequencies of 40 MHz. If the exchange is rapid the spin – spin information can be communicated by torsion fields. The spin – spin coupling constant depends on the number of covalent bonds between two interacting protons, and their geometry [48]. The phytons circulating in a vortex around the nucleus of the atom constitute a spin information matrix, a thosand times smaller than the atom itself. In the living cells the process of creating the protein building blocks making the cell functions starting with the instructions brought by messenger RNA to the Ribosomes. They have the ability to reconstruct themselves when broken down into their constituent proteins. The formative agency is not visible, but the most advanced microscopes could show, that these functions are carried out by invisible spin clusters of phytons [49]. The appearence of classical inhomogenities from quantum fluctuations we can describe by the Fourier modes of a massless free field [50] with the linear equation:

For sufficently long-wavelengts ( k ² < a´ / a) , this equation describes an unstable neural oscillator. The classical correlations are only one aspect of classical behaviour. In order to have a complete classical limit, the role of the environment is crucial, since its interaction with the system distinguishes the field basis as the pointer basis. When interactions are taken into account, classical behaviour is recovered only for open systems, in which the unobservable degrees of freedom interact with their environment [51]. When this interaction produces both a diagonalization of the reduced density matrix, and a positivie Wigner function, the quantum to classical transition is completed. We considered a model in which the system-field interacts with environmentalfield, including only its own short-wavelengts, while the initial state of the environment could be the vacuum. The influence functional (Feynman-Vernon functional) takes into the account the effect of the environment of the system [52]. The influence functional describes the averaged effect of the environmental degrees of freedom on the system degrees of the freedom to which they are coupled [53], where the environment is initially in its vacuum state.

In his relevant paper („Riemann-Einstein Structure from Volume and Gauge Symmetry“), the Nobelist F. Wilczek [54] shows that G. Shipov´s „torsion theory“ [55] is closely related to R. Penrose´s „spinors in curved spacetime“ [56] with the antisymmetric spin-connection“ as the locally induced compensating torsion fields [57]. It means locally gauging the O [1,3] subgroup of the Conformal Group. A. Akimov [58] claims that „torsion waves“ from O [1,3] of sufficient intensity to have „psychotronic weapon“ s bio-toxic effects can easily be generated in consciousness (in contrast, gravity waves from T4 are hard to find). The gravity wave T4 coupling parameter is E. Witten´s alpha superstring tension −1 . What is the corresponding O [1,3] spin connection coupling parameter ? A. Akimov means (personal communication) that it is easier to make propagating torsion dislocation topological string defects, to make propagating curvature disclination topological string defects in Macro-quantum. Vacuum Coherence Field´s „Goldstone Phase“, that´s what A. Akimov claims with Unified Exotic Vacuum Field of Dark Energy/Matter. The absolute parallelism geometry with the structural equations of Cartan [59] is:

where e^a_j is a tetrode of analytical representations of four-dimensional arbitrarily accelerated reference frame Tⁱ_kj, is the inertia field [60], Rⁱ_jkm is the Riemann tensor labelling environmental physical fields, internal field is inertia filed Tⁱ_kj, which is the carrier of energy in classical sense. The equations (1, 2) are describing non-limited four-dimensional empty space with pseudo-euclidian geometry. Its torsion is equal to zero [61]. We can then say that we have an n - parametric simple transitive group (group n T ) operating in the manifold such that are structural constants of the group that obey the Jacoby identity. The vector field ξ_bⁱ is said to be infinitesimal generator of the group [62]. We see that 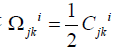, the components of the an holonomity object (Ricci´s torsion) of a homogenous space of absolute parallelism are constant (35). It is easily seen that the connection possesses a torsion. In this case 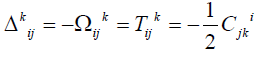where -1/2C_jkⁱ is the torsion of absolute parallelism space. It was exactly in this manner that Cartan [63] and Schouten [64] introduced connection with torsion

where ijk S is the Cartan´s torsion of the Riemann-Cartan space. The Ricci´s and Cartan´s torsions have the same symmetry properties, but Ricci´s torsion depends on angular coordinates unlike Cartan´s one. Moreover, Ricci´s torsion defines the rotational Killing-Cartan metric, but Cartan´s not at all. New concepts of fields and forces of inertia is stated in the works A. Shipov [65], allowing to see their connection with torsion fields and predict the existence in the nature of a new class reference frame systems, which were named: secondary type accelerated locally-inertial systems. As distinguished from primary type accelerated locallyinertial systems, introduced by A. Einstein [66], new systems are formed in case when the masses center of the isolated system is affected by the compensated forces of inertia, in relation to the inertial system of observation. In compliance with which the Physical Vacuum possesses the property of a hologram [9]. If the boundaries corresponding to the boundaries of the initial picture [67] are shown, the torsion image can be received far beyond these boundaries (the peripolar space photograph). Historically, the Ricci’s torsion was introduced in geometry before Cartan’s one [68] by Ricci using the rotation coefficients. It is possible to show that the Ricci’s torsion is the torsion of absolute parallelism geometry.

Let us consider the manifold at each point Xa (a = 1,2,3) specified by orthonormalized references eA, A=1,2,3, [3], where A is the number of the reference vector [32]. Actually, any reference CA is the mathematical image of a three-dimensional arbitrarily accelerated reference frame in GW of consciousness.

As it is known, Kirlian photographs are produced against an insulated sreen with a very high voltage on the other side. The high voltage [44] acts in a same way as a Torsion Field Generator with electrostatic excitation. The streamers of light picked up by the camera would then represent the way in which the Torsion Field emitted by living matter was polarised by high voltage. Brain process is essentially a search process: the brain, conditioned by earlier experience, searches by Rensink “mindsights” [68] for a satisfactory response to the new situation that the organism faces. It is reasonable to suppose that a satisfactory response will be programmed by a template for action that will be implemented by a carefully tuned pattern of firings of some collection of neurons. The neurons are too coarse-grained to explain the hard problem of the emergence of inner consciousness - of who we really are.

Gödel [67] has pointed out, that predictions are like a perception of the objects of set theory. Prediction is a mode of mathematical intuition, which in sense of perception induces building up theories of the future. The given underlying mathematics is closely related to the abstract elements contained in our empirical ideas. The brain seems to have internal theories about what the world is like. Between brains theories is a internal perceptual rivalry in Darwinian sense. The World as a quantum system can be described due the polar decomposition, as a whole system consisting from two subsystems, which are mutually observing one another. During this observation the global workspace is processing reentry between internal representations and influence functional of the environment, between left and right hemisphere, etc. Leading authors [2] are proposing to consider a j^th of k elements subset (X_j^k) taken from isolated neural system X, and its complement X − X_j^k [2]. Interactions between the subset and the rest of the system introduce statistical dependence between the two. This is measured by their mutual information 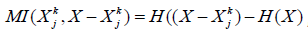, which captures the extent to which the entropy of X_j^k is accounted for by the entropy of X − X_j^k and vice versa (H indicates statistical entropy).

After the midbrain gets done processing a visual stimulus, it flows to the cortex in the posterior perceptual system, where it is preprocessed to remove constancy distortions and then processed for form, color/pitch, spatial location, state of motion. kinesthetic and sensorimotor properties, etc. For the visual system, the basic thing here is the Figure-Ground Relation--shape emerges from the background, bounded by its contours. It is axiomatic that an object is determined by its bounding contours, and it is the invariance of these under viewing conditions that determines constancy and form memory. This brings us to the domain of Lie transformation groups, denoted symbolically by the mapping G x M > G, where G is a group and M is a manifold (a surface). G is a mathematical group, a set of elements that can be “multiplied” (transformed associatively) and “divided” (there’s an identity element and each element has an inverse). G is continuous and is a manifold just like spacetime. The visual contour is a path-curve generated by the transformation group action, and there is some point on it. This is the identity element of the group.

A tangent line to the curve at that point is the infinitesimal transformation of the continuous or Lie group. The infinitesimal transformation is embodied in a Lie derivative, which drags the flow along a path-curve, the so-called “orbit”--in this case the visual contour. If £ denotes the Lie derivative and f, the visual contour, then invariance of the contour under a transformation group is shown by its being annulled by the action of the Lie derivative: £ f = 0, or by its being handed on as a “contact element” for further processing: £ f = g(f). These operations characterize psychological invariants. Because the sum of real numbers> R in SetL op is without several skills of real numbers from R, in the space in this generator of virtual reality, we can observe an extraordinal facts and phenomena’s. For example, photons without an energy, impulse, are the photon shells. Тоpos SetL op is not the only one model of a topological theory of consciousness T. Another models, another generators of the virtual reality open for us the new possible realities, but is very hard to say, which one of them is more close to our neighboring physical reality. The topological consciousness as generator of virtual reality, is reconstructing our neighboring environment due the process of perception and understanding. The algorithm, probably given us by God, is consisting from the Theorems of Morita I, II, III equivalence, and on their basis the endomorphisms are transforming the impressions, images, abstractions of Self as the consciousness. Recently 6 billions of humans are generating the same virtual reality called “the World”, by processing continuously the same God´s algorithm. And the true reality is probably behind this Carthesian Theather as the Weyl of Maya.

For us - observers at the level of organisms - a wonderful population “adjustment” to each other in the ecosystem or species in the biosphere stipulated by the re-normalization of probabilities, effect from the higher levels of biological hierarchy is “miracle” as well [66]. Similar process is the basis of all vital activity, the last cannot be understood completely inside its own or lower levels [67]. The reason for such omnicausality is in the determinance of vital processes by future, which is the present at the following hierarchy level. And every present at all degrees of biological hierarchy [69] has its own and often very complicated structure, which organizes the time in biological systems. The Bayes equation can be the part of mathematical description of probabilities re-normalization. If is considered not a model, but as a theory and, correspondingly, reflects up to a certain degree the essence of life as a process of re-normalization of probabilities, then we inevitably come to the idea of a real function on the macro-level state (ω-function) as the probability filter. Then re-normalization of probabilities at all levels from a cell up to the biosphere will be reduced to multiplicative interaction of state functions for the corresponding macro-andmicro- levels. For a cell the state function at the microlevel will be ψ-function.

The state functions of micro-and-macro-levels are not equal to each other, only when the macro-state function is marked (designated) in the macroworld. But, ω-function of consciousness is not only mapped (i.e., consciousness can topologically distinguish a characteristic state for itself out of all possible ones and make auto monitoring on the basis of endomorphisms), and also possesses time “thickness” inside of which single microstates (events) advance in a certain successions (“plots”). Such time “thickness” of macro-state which, in its turn, is developed in time, being the event of the “plot” of the following hierarchy level, results in the idea of multidimensional (at every level of the biological hierarchy - twodimensional) biological time. The role of IF is supported by recent topological theorems, and also by two Einstein principles. The first is background independence. This principle says that the geometry of spacetime is not fixed. To find the geometry, we have to solve certain equations that include all effects of matter and energy. The second principle is diffeomorphism invariance.

This principle implies that, unlike theories prior to general relativity, we are free to choose any set of coordinates to map spacetime and express the equations [30]. A point in spacetime is defined only by what physically happens at it, not by ots location according to some special set of coordinates. Diffeomorphism invariance is very powerful and is of fundamental importance. The God´s algorithm through new information is changing the probabilities of real world events at a sub-quantal level. This influence is also reaching consciousness based on reentry of probabilities, and prediction of believed future chance. The hardware of our mutual information change the correlation of neurobiology of consciousness with a influence functional (IF) of the environment. Theoretically, IF may include the God cosmic influence. The Feynman-Vernon functional is not excluding the possibility of the Shechinah and the Holy Spirit action in probabilistic mode. Second part of the reentry of Consciousness with the Influence Functional is allowing the hypothesis that God may intervene into the world events. There is an old Rabbinic tradition from the time of The Book of Esther, that the God was changed the chance (probability) concerning Persian King Ahasuerus during his sleep, and the resulting events lead to a release of the Israelites. About other paralell told in Vatican City the Pope Benedict XVI [70]: The Divine (topological – R. S.) intervention is probably the supreme arbiter of historical events.

1. Seth A, Edelman G (2004) Environment and Behavior Influence the Complexity of Evolved Neural Network. Adaptive Behavior Vol. 12.
2. Tononi G, Edelman G (1998) Consciousness and Complexity. Science 282(5395): 1846-1851.
3. Tononi G (2004) An information integration theory of consciousness. BMC Neuroscience 2(5): 42.
4. Tononi G (2004) Consciousness and the brain: Theoretical aspects. In Encyclopedia of Neuroscience (3rd Edition).
5. Raichle M (1998) The neural correlates of consciousness: an analysis of cognitive skill learning. Philos Trans R Soc Lond B Biol Sci 353(1377): 1889-18901.
6. Wilczek F (1998) Riemann-Einstein Structure from Volume and Gauge Symmetry. Phys Rev Lett p. 80.
7. Gabor D (1946) Theory of Communication. J of the Institute of Electrical Engineers pp. 429-457.
8. Penrose R (1994) Shadows of the Mind: A search for the missing science of consciousness. Oxford UP Oxford.
9. Pribram KH (1991) Brain and Perception. L Erlbaum Associates Publishers Hilsdale
10. Pribram KH, Hilsdale NJ (1993) Rethinking Neural Networks: Quantum Fields and Biological Data Proc. Of the First Appalachian Conf On Behavioral Neurodynamics. L Erlbaum Publ.
11. Prigogine I, Stengers A (1984) Order out of Chaos. Bantam Books New York, USA.
12. Beggs J, Plenz D (2003) Neuronal Avalanches in Neocortical Circuits. The Journal of Neuroscience 23(35): 11167-11177.
13. Bak P, Tang C, Wiesenfeld K (1987) Self-organized criticality: an explanation of the 1/f noise. Phys Rev Lett 59(4): 381-384.
14. Herz AV, Hopfield JJ (1995) Earthquake cycles and neural reverberations: collective oscillations in systems with pulse-coupled treshold elements. Phys Rev Lett 75(6): 1222:1225.
15. Mriganka Sur (2005) Invariant computations in local cortical networks with balanced excitation and inhibition. Nature Neuroscience 8(2): 194-201.
16. Zheng Wu, Gary Yen (2003) A SOM Projection Technique With The Growing Structure For Visualizing High-Dimensional Data. International Journal of Neural Systems 13: 5.
17. Shuai J, Durand D (2003) Strange Nonchaotic Attractor In Hugh- Dimensional Neural System. International Journal of Bifurcation and Chaos 13(1).
18. Kobozev NI (1971) Investigations in the Field of Thermodynamics and Thinking Processes. Moscow (in Russian).
19. Mikhailovsky GE (1981) Negative entropy and dissipative structures initiated by the limited cycles. J of Phys Chem p. 55.
20. Von Neumann J (1956) Probabilistic logic and the synthesis of reliable organisms from unreliable components. In Automata Studies Princeton, New Jersey, USA
21. Prigogine I (1980) From Being to Becoming. Time and Complexity in the Physical Sciences. San Francisco.
22. Mikhailovsky GE (2000) Biological Time, Its Organization, Hierarchy And Representation By Complex Values. Ereports.
23. Davidson RJ (2004) Long-term mediators self-induce high-amplitude gamma synchrony during mental practice. PNAS 101(46): 16369- 16373.
24. Baars B (1988) A Cognitive Theory of Consciousness. Cambridge UP, New York, USA.
25. Dehaene S, Kerszberg M, Changeux JP (1998) A neuronal model of a global workspace in effortful cognitive tasks. PNAS 95(24): 14529- 14534.
26. Shannon CE, Weaver W (1963) The Mathematical Theory of Communication.University of Illinois Press Urbana.
27. Wheeler JA (1968) Einsteins Vision. Springer-Verlag.
28. Hehl FW (1973) Spin and Torsion in General Relativity. Foundations GRG 4(4): 333-349.
29. Shipov GI (1997) A Theory of Physical Vacuum. Theory, experiments and technologies. Moscov Nauka p. 450.
30. Belinfante FJ (1939) On the Spin Angular Momentum of Mesons. Physica p. 9.
31. Dubrovsky A (1985) Elastic model of physical vacuum. DAN SSSR 282(1).
32. Akimov AE (1994) The action of the torsion fields on the melted tin. Moscow CISE VENT preprint p. 49.
33. Akimov AE (1995) Torsion communications of the third thousand years. Proceedings of “Modern telecommunications technologies” Moscow.
34. Weitzenbock R (1923) Invariantentheorie. Groningen Noordhoff p. 320
35. Schouten J (1954) Ricci-Calculus: An Introduction to Tensor Analysis and Its Geometrical Applications. Heidelberg, Springer, London.
36. Cartan E, Schouten J (1926) Proc Knkl Nederl Akad p. 29.
37. Nishikava T, Ying-Cheng Lai, Hoppensteadt, (2004) Capacity of Oscilatory Associative-Memory Networks with Error-Free Retrieval. Phys Rev Let p. 92.
38. Hoppensteadt FC, Izhikevich EM (2000) IEEE trans. on Neural Networks p. 11.
39. Hoppensteadt FC (1989) Intermittent chaos, self-organization, and learning from synchronous synaptic activity in model neuron networks. PNS USA 86(9): 2991-2995.
40. Wiener N (1961) Cybernetics. MIT Press Cambridge MA.
41. Von Neumann J (1958) The Computer and the Brain. Yale Univ Press, New Haven, USA.
42. Turing AM (1936-1937) Proc. London Math Soc 5.
43. Shapiro J (2004) The Hopfield Model As Auto-associative Memory Lecture. Department of Computer Science, University of Manchester.
44. Dyatlov VL (1999) Linear equations of macroscopic electrogravidynamics. ANS
45. Dmitriev AN, Dyatlov VL (1996) A model of non-homogenous physical vacuum and natural self-Luminous formations. IICA, Novosibirsk.
46. Gell-Mann M, Hartle JB (1990) in Complexity, Entropy, and the Physics of Information. Zurek WH (Eds.). Addison-Wesley, Reading.
47. Paz JP, Zurek WH (1999) Environment-Induced Decoherence And TheTransition From Quantum To Classical. 72nd Les Houches.
48. Hopfield JJ (1982) Proc Nat Ac Sci p. 79.
49. Heaviside OA (1893) Gravitational and Electromagnetic Analogy. The Electrician.
50. Doya K (1999) What are the computations of the cerebellum, the basal ganglia, and the cerebral cortex. Neural Networks 12: 961-974.
51. Doya K (2002) Metalearning and Neuromodulation. Neural Networks 15: 4-5.
52. Reynolds JN, Wickens JR (2002) Dopamine-dependent plasticity of cortico-striatal synapses. Neural Networks 15(4-6): 501-521.
53. Tremblay L, Schultz W (2000) Modifications of reward expectationrelated neur act during learning in primate orbitofrontal cortex. J of Neurophys 83(4): 1877-1855.
54. Posner MI, Raichle ME (1994) Images of Mind. Scientific American Library NY.
55. Marlin B (1999) Collaborative Filterring: A Machine Learning Perspective. Toronto, USA.
56. Dempster AP, Laird NM, Rubin DB (2004) Maximum likelihood from incomplete data via the EM algorithm. J of the Royal Statistical Society Series p. 39.
57. Zeki S (2001) Localization And Globalization In Conscious Vision. Annu Rev Neurosci 24: 57-86.
58. Ax J, Kochen S (2002) Extension of Quantum Mechanics to Individual Systems. Princeton Univ Press.
59. Zurek WH (1991) Decoherence And The Transition From Quantum To Classical. Physics Today October.
60. Popper KR (1982) The Open Universe: An Argument for Indeterminism. Cambridge, UK.
61. Prigogine I (1997) The End of Certainty. Time, Chaos and the New Laws of Nature. New York, The Free Press, USA.
62. Schrödinger E (1945) What is Life ? Cambridge UP
63. Riesz F, Sz-Nagy B (1991) Functional Analysis. New York Dover, USA.
64. Bohr N (1958) Atomic Physics and Human Knowledge. New York, Wiley, USA.
65. Penrose R (1994) Shadow of the Mind. Oxford UP, New York, USA.
66. Wigner EP (1983) In Quantum Optics, Experimental Gravitation, and the Measurement. Theory P Meystre (N Scully Eds) Plenum, New York, USA.
67. Gödel K (1947) What Is Cantor´s Continuum Problem ? The American Mathematical Monthly p. 54
68. Rensink R (2000) Visual Search for Change: A Probe into the Nature of AttentionalProcessing. Visual Cognition p. 7.
69. Feynman R, Vernon F (1963) Ann Phys 24: 118.
70. Vatican Information Service (2005) 050511 (400).