Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Bruno Mario Cesana*1,2
Received: June 20, 2018; Published: July 06, 2018
*Corresponding author: Bruno Mario Cesana, Department of Molecular and Transactional Medicine, Statistics and Biomathematics Unit, Faculty of Medicine and Surgery, University of Brescia, Brescia, Italy
DOI: 10.26717/BJSTR.2018.06.001359
Statistical significance is a tool for making decisions on a probabilistic basis extensively used in the scientific world. It must be recognized that the 0.05 value as the threshold of the statistical significance is undoubtedly arbitrary and nothing prevents it from being modified according to well-founded arguments. Furthermore, it must also be recognized that the logic of the statistical significance test is quite debatable, as well as being little understood by researchers who are the main users. Also the meaning of p-values is often ignored with consequent misinterpretations and misunderstandings. I will give a general overview and some insights on the topics of the p-values and of the statistical significance.
Keywords: Statistical Significance; True Null Hypothesis; Bayes Factor; Prior and Posterior Probabilities; Prior and Posterior Odds; False Discovery Rate; Claims of New Discoveries; Irreconcilability; Null Hypothesis Significance Testing Procedure; Strength of Evidence
Recently, seventy-two eminent biostatisticians, psychologists, philosophers, science methodologists, economist, etc. (let’s define them, generally, as scientists) propose “to change the default P-value threshold for statistical significance from 0.05 to 0.005.” [1]. The proposal has been motivated by the “the lack of reproducibility of scientific studies” and by the fact that “the statistically significance threshold of the P<0.05 gives a high false discovery rate”, even in the absence of any flaws in the experimental design, conduction of the study, statistical analysis and reporting of the results. Moreover, it has to be stressed, that the proposal applies to “claims of new discoveries” and that “should not be used to reject publications of novel findings with 0.005 To deepen these topics very useful references, among others, are the landmark paper by Berger and Sellke [7] with the very impressive title of “The Irreconcilability of P-Values and Evidence” together with six companion commentaries in the issue of March, 1987 of the Journal of the American Association and the paper by Goodman [8]. In addition, also the paper by Moran and Salomon [9] has to be particularly recommended, owing to its pretty exhaustive review of the statistical test theory also from the historical point of view. Indeed, the debate on the statistical significance test goes back to the first work of Fisher and to those of Neyman and Pearson together with the disputes between Fisher and Neyman (mainly), as it has been reported, among others, in some books [10-12] to which readers are referred. In addition, it has to be said that the proposal of moving the significance threshold from 0.05 to 0.005 has been previously formulated by Johnson [13], one of the authors of the paper of Benjamin et al. [1] This proposal has been commented by two letters [14,15] with a reply by Johnson [16] to which the interested readers are referred. Finally, the very impressive Ioannidis’s paper “Most Published
Research Findings Are False” [4] has been commented by Jager
& Leek [17] who reported a substantial reduction of the “false
discovery rate” to 14% leading to the conclusion that “the medical
literature remains a reliable record of scientific progress”. However,
the Jager and Leek’s paper has been furtherly criticized by six
companion commentaries [18-23] in the same issue of Biostatistics
with, not surprisingly, very different judgements and considerations.
Indeed, it is very well instructive to see how many aspects can be
raised by a statistical method together with its practical realization.
However, as a general conclusion, it seems that the drastic and
dramatically alarming Ioannidis’s statement [4] has to be mitigated
to some extent. Coming back to the meaning and the interpretation
of the p-values, it is important to stress that Ioannidis reported
[3], according to Wasserstein & Lazar [24], that the most common
misinterpretation of p-values, among the multiple ones present in
the scientific literature, is that they represent the “probability that
the studied hypothesis is true”. So, according to this misunderstanding, “a P value of .02 (2%) is
wrongly considered to mean that the null hypothesis (eg, the drug is
as effective as placebo) is 2% likely to be true and the alternative (eg,
the drug is more effective than placebo) is 98% likely to be correct”
[2]. These wrong interpretations are not surprising since it is very
well known the poor feeling that researchers have for Statistics and
for the scientific reasoning based on the statistical methodology.
Also some comments, particularly raised in the case of negative
controlled clinical trials and only based on some clinical reasoning
[25] without considering the corresponding statistical aspects [26],
turn out to be rather questionable or, at least, definitely incomplete. The difficulties of a correct interpretation of the p-values
even led to banish the p-values from the Basic and Applied Social
Psychology (BASP) journal; indeed, after a grace period of one
year, announced by the first Trafimow’s Editorial [27], the editors
announced that BASP “would no longer publish papers containing
P-values, because the values were too often used to support lowerquality
research” [28]. Furthermore, in their Editorial, the Editors
emphasized that “the null hypothesis significance testing procedure
(NHSTP) is invalid, and thus authors would be not required to
perform it.” So, if this decision will be shared by other journals,
we can also arrive at a situation of no p-values at all in the papers
of the scientific literature. The BASP journal announcement has
been commented by Nature [29]. This fact confirms the attention
of Nature to the role of the Statistics in the scientific research and
to the meaning of the p-values, as the publication of the paper by
Nuzzo [30] and of the companion editorial [31] furtherly attests. Nuzzo’s paper [30] succeeded in drawing the attention of
a large audience of physicians on the Bayes’s rule, previously
introduced in the epidemiological context by some papers written
by Goodman [32-35]. In fact, Nuzzo’s paper [30] shows very clearly,
in a figure, how p-values of 0.05 or 0.01, empirically obtained
from a statistical analysis, can modify three values of the a “priori
odds” that the null hypothesis (H0) is true; namely: “19 to-1 odds
against the null hypothesis”, “1-to-1 odds”, and, finally, “9-to-1
odds in favor of the null hypothesis”. I think that discovering that
a p-value of 0.05 or even 0.01 can have a very little impact on the
plausibility of an almost unlikely null hypothesis (19 to-1 odds or
P=0.95 against) and that only in the case of a very plausible H0 (9-
to-1 odds or P=0.90 in favor) the p-values are very similar to the H0
probabilities, could have made it clear the difference between the
statistical significance and the probability that H0 has of being true.
Furthermore, Nuzzo’s paper [30] made it clear that: a) the statistical test is carried out considering true the null
hypothesis b) how this assumption is in fact questionable c) Finally, how it is practically not sensible to reason in terms
of a “true null hypothesis” for concluding in the terms of the
evidence of a clinical research. Indeed, the message very well
spread by this paper is that the null hypothesis, assumed to be
absolutely true under the paradigm of the statistical significance
test, has actually an unknown probability of occurring and that
it is sensible to consider different probability scenarios of the
veracity of H0 The only criticism that could be done on Nuzzo’s paper [30]
consists in the fact that have not been shown the formulas of the
Bayes factor, leaving its role not very well defined; in addition, it has
not reported which Bayes factor has been used for the calculations
shown in the figure. Indeed, the pertinent answers to the questions
related to the statistical methodology must be found by the
reader in the referenced papers. An additional merit of Nuzzo’s
paper [30] was of leading the American Statistical Association to
express its official position and thought about the meaning of the
p-values in some papers [24,35] and also to publish on YouTube a
very instructive video of the statistical section “ASA statement on
P-values and statistical significance: Development and impact” with
speakers Nuzzo, Johnson, and Senn [36]. A further explanation of p-value has been given by Mark et al.
[37] and also a non-technical introduction to the p-value statistics
has been reported by Figueiredo Filho et al. [38]. In addition,
several formally correct videos on the topic of the p-values are
on YouTube [39-41] together with one very amusing featuring
cartoons as protagonists [42]. I do not want to make considerations
about the philosophy of the science or on the role of the Statistics
in the scientific research or to propone a new paradigm of the
scientific method. Furtherly, I must say that I do not even share the
controversy raised by some statisticians who would like only the
intervals of confidence to be used instead of the statistical tests,
because I think that both must be used, given that both provide
useful information about the results of the statistical analysis of a
research. Indeed, the problem is always of interpreting correctly the
results of the statistical procedures and of knowing their meaning.
As a biostatistician, more oriented in sample size calculations
and clinical trials methodology, my aim is to point out the correct
interpretation of the p-values together with some personal
suggestions about their use focused also on the plausibility of the
null hypothesis or to the probability that a null hypothesis has to
be true. According to Fisher [43] the p-values could be considered as
an index of the “strength of the evidence” against H0. Particularly,
after having choose the statistical test, carried out the experiment,
calculated the test statistic from the actual experimental data
and the probability value associated with the test statistic, if this
probability value is quite small (say, ≤0.05) the null hypothesis
could be rejected. However, it would be better to use the expression
“to not accept”, according to a less strong expression that is
more relevant to the probabilistic nature of the statistical testing
procedure. Actually, Fisher popularized the use of the p-values
in statistics and, particularly in his influential book Statistical
Methods for Research Workers [44], proposed the level p = 0.05,
or a “1 in 20 chance of being exceeded by chance”, as a limit for
statistical significance. Then Fisher reiterated the p = 0.05 threshold and explained
its rationale, stating: “It is usual and convenient for experimenters
to take 5 per cent as a standard level of significance, in the sense
that they are prepared to ignore all results which fail to reach this
standard, and, by this means, to eliminate from further discussion
the greater part of the fluctuations which chance causes have
introduced into their experimental results” [44]. So, a p-value of
≤0.05 on the null hypothesis indicated, according to Fisher [44],
that: “Either an exceptionally rare chance has occurred or the
theory is not true”. Fisher’s further advice [44] was that “If one in
twenty does not seem high enough odds, we may, if we prefer it,
draw the line at one in fifty…or one in a hundred”. Furtherly, in the Statistical tables for biological, agricultural
and medical research compiled with Yates [45] there are reported
the quantiles of several probability distributions (standardized
Gaussian: (Table 2). The Normal Probability Integral; Student’s t:
(Table 3). Distribution of t; c2: (Table 4). Distribution of c2, and F:
(Table 5). Distribution of z and Variance Ratio for 20%, 10%, 5%,
1%, and 0.1%; thereafter it was called F distribution in honor of
Fisher or F distribution shortly for the distribution of Fisher and
Snedecor) for selected probability values. So, the computed values
of the statistical tests could be compared against some cut-offs
corresponding, especially, to the p-values of 0.05 (mainly) and 0.01,
cementing their use as statistical significance thresholds. A basic point, perhaps not very well understood, is that the
inference from the p-value involves only the null hypothesis
and that the “likelihood” of this hypothesis, calculated from the
experimental data, is not also the “probability of the null hypothesis
of being true”. That is, the p-values should not to be misinterpreted
as posterior probabilities that have to be obtained according to the
Bayesian paradigm. However the main relevant and frequent use
of the p-values is currently in the context of the Neyman-Pearson
hypothesis testing frequentist paradigm, in which two hypotheses
are formalized; namely the null hypothesis (H0) and the alternative
(H1 or HA), with the first to be tested versus the latter. Then, the test
statistic is obtained from the formula of the pertinent statistical test
and the corresponding probability value is calculated by referring to
the probability distribution of the test statistic. It has to be pointed
out that currently, the p-values are compared with the prefixed
significance level instead of comparing the test statistics with the
tabulated critical values that delimit the critical region of rejection
(not acceptance) of H0 of the pertinent probability distribution. In fact, the diffusion of statistical software that calculates
the probability values has made the consultation of tables quite
obsolete. Furthermore, one thing is to state that the p-value is
<0.05 and another is to report its exact value (to a certain number
of decimal places) such as p = 0.0253. It has to remember that the
critical region corresponds to an area of a probability distribution,
and, therefore, to a probability value that is equal to the significance
level, chosen by the researcher and defined as α at the left or right
tail of the distribution in the case of a unilateral test or equal to α/2
at the left and right tail of the distribution in the case of a bilateral
test. In the frequentist paradigm, are relevant the type I error (α)
that corresponds to the probability of rejecting (not accepting) a
true null hypothesis, and the type II error (β) that corresponds
to the probability of not rejecting a false null hypothesis or, more
known and quoted, the power of the statistical test given by 1-β. In
fact, this procedure refers to the repetition of the same experiment
carried out under the same conditions on samples repeatedly
and randomly obtained from the same distribution (H0 is true) or
from two (at least) different distributions just in agreement to the
alternative hypothesis. Finally, it has also to consider the Jeffreys’s approach to testing
in the Bayesian context [7]. This method requires the definition of
the Bayes factor as the ratio between the value of the maximum
likelihood calculated from the experimental data under the null
hypothesis (given the parameter under H0 equal to θ0, say) and the
value of the likelihood calculated from the experimental data under
the alternative hypothesis (given the parameter under H1 equal to
θ1, say). Then the null hypothesis is rejected if the calculated ratio
is <1 or, otherwise, if the value of the calculated ratio is >1, the
null hypothesis is not rejected. Thereafter, it is possible to report
the posterior probabilities (the probability that H0 is true given
the experimental data) by transforming the odds (the calculated
Bayes factor) in a probability by recalling that probability (p) is
obtained as p = 1 / (1 + odds). Finally, is also possible to calculate
the posterior probability for the alternative hypothesis of being
true, given the experimental data. Considerations about the disagreement and the sparse points
of agreement among the three giants Fisher, Neyman (with also E.
Pearson) and Jeffreys are out of the limits of this editorial. Useful
papers for some further insights are from Berger and Sellke [7],
Hubbard and Bayarri et al. [47], Gibbons[48], Pratt et al. [49], De
Groot [50], Christensen [51] and finally, Berger [52]. It has to be
stressed that instead of to reject, I always used the expression to not
accept just for underlying the probabilistic nature of the statistical
testing procedure; otherwise, it has to be used the expression not
rejected since the expression to accept has to be absolutely avoided
owing to the fact that, according to the scientific paradigm, the null
hypothesis can be only disproved. However, it has to be said that the
expression accept the null hypothesi is currently used also in the
statistical literature [53]. Finally, it has to be point out the fact that if
the null hypothesis is not rejected, nothing could be concluded, and this
is a point not well understood by clinical researchers. To this
point it has to be remembered the sharp and definite sentence: “the
absence of the evidence is not the evidence of the absence”. The p-value quantifies the probability of having obtained
the experimental results “under the null hypothesis (H0)” that is,
usually, a hypothesis of no difference. Let’s disregard for sake of
simplicity the case of the non-inferiority settings in which the null
hypothesis is of the “maximal difference not clinically/biologically
relevant” and the recently considered superiority statistical
testing in which the null hypothesis is of the “minimal difference
clinically/biologically relevant” [53]. The expression “under the
null hypothesis (H0)” can be better paraphrased as “if the null
hypothesis is true” but it is, maybe, only with the expression “given
that the null hypothesis is true (p-value | H0) that it is very well
stated and understandable that the p-value of the statistical test is
obtained as a conditional probability. So, considering the formula of the conditional probability,
the probability of H0 of being true is equal to 1 [P(H0) = 1] by the
assumption underlying the statistical test of significance, and,
consequently, the probability of the joint event given by a statistical
significant result [P(xOBS)≤0.05)] and H0 true [P(H0) = 1], defined
as [P(xOBS ∩H0)] remains equal to the simple probability value
(p-value) associated with the test statistic. Being the formula of a
conditional probability given by: Where xOBS indicates the observed Result. It is well evident that
a value equal to 1 at the denominator does not change the value
at the numerator. It is also evident that the assumption “the null
hypothesis is true” is useful for carrying out the test of significance
and for being able to conclude against the null hypothesis or to
make no conclusions at all. However, it is also well evident that
in the real world there cannot exist a “true null hypothesis” or a
“true alternative hypothesis”. It is possible to argue that there is a
situation “equipoise-like” in which the two hypotheses are equally
probable of being true [P (H0) = P (HA) = 0.5] or situations in which
P(H0) > P(HA) or P(H0) < P(HA), taking also into account the context
of the research. So, it must reasonably be said that this paradigm
is a useful tool for concluding about a research (a decisional rule
on a probabilistic basis) but it is not adequate to conclude on the
veracity of the null hypothesis. To this aim it has to consider a
different approach built on the Bayesian theory. For calculating the probability of the null hypothesis of being
true it is necessary to refer to the “Bayes factor” that represents
the evidence from the data, and the value of the “prior odds” that
has to be obtained, according to Benjamin et al. [1] “by researchers’
beliefs, scientific consensus, and validated evidence from similar
research questions in the same field.” Benjamin et al. [1] shows the
application of the calculations focused on the truth of the alternative
hypothesis (H1) against the null hypothesis (H0), but for keeping
consistency with the familiar statistical testing paradigm focused
on the null hypothesis, I will consider the opposite situation of the
truth of the null hypothesis (H0) against the alternative hypothesis
(H1), which involves the reversal of the likelihood ratio. So: Where the Bayes factor has to be calculated by considering the
distributional properties of the observed data. It has to remember
that the odds corresponds to the ratio between a probability and
its complement to 1; so, for a priori probability equal to 0.95 very
unfavorable for the null hypothesis of being true, the a priori odds
is 0.95/0.0.05 = 19 or for a priori probability very favorable for
the null hypothesis of being true equal to 0.90 the a priori odds is
0.90/0.0.10 = 9. Furthermore, we obtain an odds value of 1 for a
probability of 0.5 and of 0.33 for a probability of 0.25, respectively. Then, by multiplying the prior odds by the Bayes Factor, it is
possible to calculate the posterior odds that, for an easy reading, can
be converted in a probability value by remembering that p = odds /
(1 + odds). For example, with BF of 0.2, 0.1, 0.05, and, finally, of 0.01
the above prior odds of 19 against the null hypothesis give posterior
odds of 3.8, 1.9, 0.95, and 0.19. It is straightforward to obtain the
corresponding posterior probability values of 0.792, 0.655, 0.487,
and 0.159. Again, for the above prior odds of 9, we obtain posterior
odds of 1.8, 0.9, 0.45, and 0.09 with the corresponding posterior
probability values of 0.643, 0.474, 0.310, and 0.083. It has to be
said that the above Bayes factor values correspond, according to
Goodman [33b] to a “Strength of Evidence” “weak”, “moderate”,
“moderate to strong”, and, finally “strong to very strong”,
respectively. Apart from considering some particular values of the
Bayes Factor as shown before, it is very useful to consider that in
the case of statistical tests based on the Gaussian distribution, as
usually happens in the biomedical research, the “minimum Bayes
Factor” is obtained by: Where “z” is the quantile of the standardized Gaussian
distribution corresponding to the obtained p-value; for instance z
= 1.28155 for a p-value = 0.90, z = 1.6448 for a p-value of 0.95, z
= 1.88079 for a p-value = 0.97, z = 1.95996 for a p-value = 0.975,
z = 2.32635 for a p-value of 0.99, and, finally, z = 3.09023 for a
p-value of 0.999. It has to be noted that the “Minimum Bayes
Factor” corresponds to the strongest Bayes factor against the null
hypothesis. Unfortunately, in Table 1 of the Goodman’s paper [34]
it has not reported that the probability values shown on the first
column under the heading “P Value (Z Score)” has to be considered
as two tailed. So, the values of the Minimum Bayes Factor shown
on the second column are, obviously, only correct for the two
tailed probability value obtained by dividing by two the values
shown in the first column. In any case, a substantial decrease of the
probability of the null hypothesis of being true has been obtained
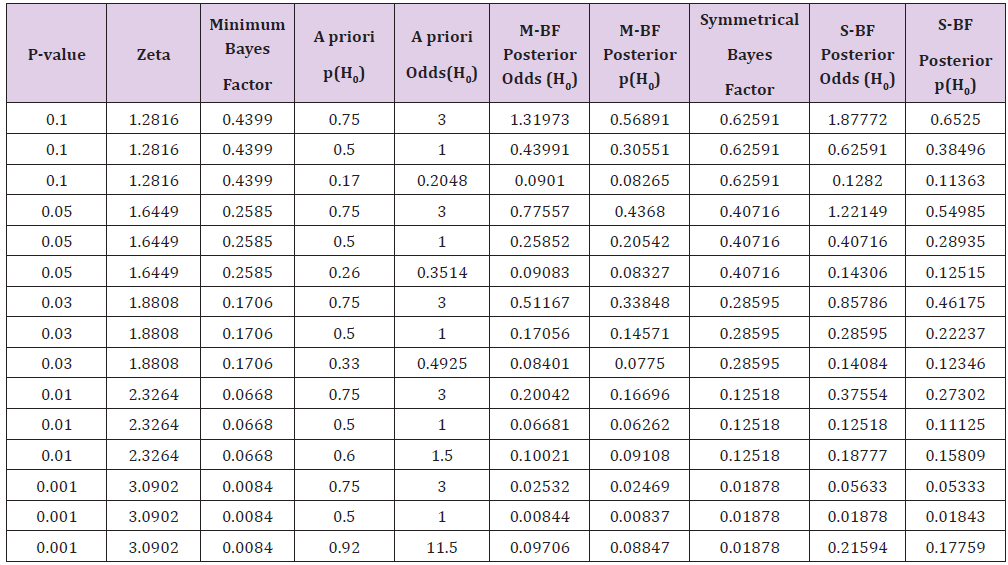
for all the situations shown in the table. Table 1: Values of the posterior probabilities of the null hypothesis (H0) of being true according to some values of the a priori odds
calculated from the p-value obtained from the experimental data. Values of the “Minimum Bayes Factor (M-BF)” and of the “Symmetrical
Bayes Factor” (S-BF) are shown. Table 1 of the Goodman’s paper [33] has to be corrected as
the following Table 1 shows for the part on the left regarding the
Minimum Bayes Factor column and those that the M-BF Posterior
odds and M-FB Posterior p(H0). It has to be stressed that, in this
case, the five values of the minimum Bayes Factor shown in Table 1
have been defined as a “weak”, “moderate”, “moderate”, “moderate
to strong”, and “strong to very strong”. It is an obvious consideration
that a Bayes Factor equal to 1/10 for the null hypothesis against
to the alternative hypothesis, it means that these study results
have decreased the relative odds of the null hypothesis by 10-fold.
Furthermore, it has also to consider that, the minimum Bayes factor
described above does not involve a prior probability distribution
over the non-null hypotheses and, consequently, it is a global
minimum for all prior distributions. However, there is also a simple
formula for the minimum Bayes factor in the situation where the
prior probability distribution is symmetric and descending around
the null value. This is given by: Where p is the p-value associated to the statistical significance
obtained from the experimental data[3]. This symmetrical Bayes
factor has been used in Nuzzo’s paper [30] the last three columns of
the above Table 1 report the values of the “minimum Bayes Factor
for a symmetric prior probability distribution (Symmetrical); it
has to be noted that the decrease of the probability is lower than
that obtained by the minimum Bayes factor. Finally, it has also to
mention the “objective” posterior probabilities that can be obtained,
according to Jeffreys as reported by Berger [51]. For a Bayes factor
calculated according to the above equation 2, the probabilities for
H0 and H1 are respectively: The above expressions are pertinent to the case of a prior
probability equal to 0.5, leading to calculated prior odds of 1. So, the
posterior odds are just equal to the Bayes factor and then, it has to
apply the usual formula already shown for obtaining a probability
value from odds. The formula for calculating the posterior
probability of the alternative hypothesis (p (H1)) is obtained by
considering that it has to be use the reciprocal of the Bayes factor
calculated for the null hypothesis. By substituting BF(xOBS) with 1/
BF(xOBS) in the first formula the second is easily obtained. To this
regards, it can be said that a p-value of 0.005 gives M-BF = 0.03625
and a S-MF = 0.07201 instead of 0.25852 and 0.40716 respectively
obtained by a p-value = 0.05. This fact has an important consequence
on the posterior H0 probability of being true that for a p-value =
0.005 remains <0.05 until a prior p(H0) ≤0.55 (at least) against H0
instead of p(H0) ≤0.15 (at least) in the case of p = 0.05. For sake of
clarity, the above calculations have been done with the values of
the minimum Bayes factor and with an increase of p(H0) in steps of
0.05 from 0.05 to 0.95. Finally, it has to be noted that a probability
against H0 is actually in favor until a value of 0.5 Phase II clinical trials in Oncology tend to consider higher
significance levels (ranging from 0.05 to 0.20) for reducing the
number of the patients to be enrolled and, consequently for having a
faster screening of the drugs potentially interesting for being tested
for efficacy in a larger Phase III trial [54]. Furthermore, according
to Jung [55], phase II trials in order to lower the sample size “use
a surrogate outcome rather than a confirmatory endpoint and
one-sided α of 0.05 to 0.20 and a power of 0.80 to 0.90, compared
to two-sided α of 0.05 and a power of 0.90 or higher in phase III
trials”. Also the threshold for declaring a pharmacodynamics effect,
as in the Phase 0 trials, is preferably put at 0.10 [56]; it has to be
considered that Phase 0 trials allow to establish feasibility and
to refine the trial methodology for anticancer drugs in a limited
number of patients before a large number of patients are exposed
to toxic doses of the study agent. The importance of reducing the number of the patients to be
enrolled in Phase II trials is well documented also by the proposal
of Khan, Sarker and Hackshaw [57] consisting in accepting an “α
level that is ‘around’ 10% and a power ‘around’ 80%”, by exploiting
the sawtooth behavior of the α and power function of the exact
binomial statistical test [58]. For example, for demonstrating a
difference from 0.10 to 0.20 with significance level (α) of 0.05 and
power (1-β) of 0.80, the calculated sample size is of 78 subjects with
13 successes as the critical number for not accepting H0. However,
owing to the above mentioned sawtooth behavior, the actual values
of α and 1-β are 0.0453 and 0.8081, respectively. Moreover, by
accepting α = 5.67% and power = 77.7%, both close to the required
levels of 0.05 and 0.80, the sample size is of 65 with a relevant
saving of 13 subjects (16.7%). A useful and exhaustive review on Phase II designs is from
Mariani & Marubini [59]; this review is relevant also from the
historical point of view since it summarizes all the main statistical
methodology until the year of its publication. Finally, it has to
be remembered, almost like a curiosity, that the FDA guidance
[60] reports that the Center for Veterinary Medicine “generally
considers a significance level of α = 0.10 useful as a conservative
screen for identifying potential treatment-related safety concerns
among endpoints in Target Animal Safety studies”. In addition, also
“Pairwise mean comparisons between each treatment against the
control group are also performed using an unadjusted α = 0.10.”
So, as a conclusion, in preliminary trials of anticancer drugs the
proposal of lowering the significance threshold seems rather
questionable and problematic. It is obvious that moving the significance threshold from 0.05 to
0.005 there is an important increase in the sample sizes necessary
to be enrolled in a trial, keeping fixed the other ingredients of the
sample size calculation that are the effect size or difference and
variability for continuous variables, the difference and the baseline
proportion for qualitative variables, the power and the statistical
significance test. The paper from Benjamin et al. [1] reports that
“for a wide range of common statistical tests, transitioning from a
P-value threshold of α = 0.05 to α = 0.005 while maintaining 80%
power would require an increase in sample sizes of about 70%”. It is worthwhile to underline that it could be argued that the
switching from 0.05 to 0.005 actually refer to a switch from 0.025 to
0.0025 since the ICH E guideline [61] refers to a two-sided statistical
test. It had to be noted that in the case of a sample size calculation
for an unpaired Student’s t test, power of 0.80 and effect size values
ranging from 0.25 to 2.5 by step of 0.01, the increase of the sample
size is globally of about the 65.97% for a power of 0.80. Then there
is a decrease for increasing values of the power; for instance, it is of
63.62% for a power of 0.85 and becomes of 59.60% for a power of
0.90, as a further demonstration of the non-linearity relationships
between the two functions of the statistical significance (α) and
of the power (1-β). In any case the sample size increase has to be
judged as relevant and, maybe, not ethically acceptable given the
current limitations of the number of patients who can be actually
enrolled in clinical trials and of the economic resources available. Benjamin et al. [1] recognized that only fewer studies could
be effectively conducted using current experimental designs and
budgets. Furthermore in Figure 2, they showed the benefit of this
p-values switching and its consequences; particularly, they stated
without any further explanation that the “false positive rates would
typically fall by factors greater than two”. Then, Benjamin et al. [1]
concluded with a series of documented claims such as “Increasing
sample sizes is also desirable because studies with small
sample sizes tend to yield inflated effect size estimates [62], and
publication and other biases may be more likely in an environment
of small studies [63]” and self-citations such as “considerable
resources would be saved by not performing future studies based
on false premises” and “We believe that efficiency gains would far
outweigh losses” that, of course, have to be demonstrated. In any
case, the huge increase in sample size calculation has a dramatically
economic impact, and, above all, a series of ethical consequences
that have to be appropriately considered and resolved. Recently Combes et al. [64,65] published on a top medical
journal an international controlled trial comparing venovenous
extracorporeal membrane oxygenation (ECMO) with the usual
standard of care, but allowing for the patients in the control group
the Crossover to ECMO if they had refractory hypoxemia. The
primary end point was mortality at 60 days. The key secondary
end point was treatment failure, which was defined as crossover
to ECMO or death in patients in the control group and as death in
patients in the ECMO group. It is very well known that the acute
respiratory distress syndrome (ARDS) is a very severe disease
associated with a high mortality exceeding 60%. Then it is very
understandable the expectation that this trial had aroused in the
medical world, particularly in physicians working in the Intensive
Care Unit. The sample size calculation was based on a very sophisticated
statistical methodology such as group sequential analysis,
triangular test, etc. that it is not possible to comment in depth
here. However it has to be said that the trial had the ambitious aim of demonstrating a 20% reduction in the expected mortality
at 60 days (60% in the group receiving conventional ventilation vs.
40% among those receiving early ECMO support). Accordingly, it
has be stated: “for a 80% power, at an alpha level of 5% and with
a group sequential analysis occurring after the randomization
of every 60 participants, the maximum sample would need to be
331 participants.” Furthermore the statistical analysis was very
complicated by the fact that 28% of the patients in the control
group crossed over to ECMO for refractory hypoxemia. About this
it has to report what the authors very correctly wrote “We were
aware of this potential problem when we started the trial, but many
investigators felt that it would have been unethical to prohibit
crossover to ECMO in patients with very severe hypoxemia”. Unlikely, the statistical analysis on the primary end point at
60 days showed a relative risk of 0.76; 95% confidence interval
[CI], 0.55 to 1.04; P = 0.09. Also an additional statistical analysis
(log-rank test), actually carried out according to a not justifiable
criterion in my opinion, showed a result not statistically significant:
“the hazard ratio for death within 60 days after randomization
in the ECMO group, as compared with the control group, was
0.70 (95% CI, 0.47 to 1.04; P = 0.07)” Finally, also a multivariable
analysis gave not statistically significant results, as the authors
wrote: “Adjustment for important prognostic factors did not change
the results.” However, the fact that it is has not clearly stated how
these results have been obtained and, consequently, that they
cannot be reproduced is, in my opinion, particularly disturbing.
For example if we carry out a simple c2 analysis of the 44/124
vs. 57/125 proportions of events in the ECMO and control group,
respectively as the Table 1 of Combes et al. [64] shows, we obtain:
Chi-Square = 2.6423 with p = 0.1041 and a Continuity Adjusted
Chi-Square = 2.2393 with p = 0.1345, very different from the p =
0.09 reported. Finally, at the Fisher’s exact test the two-tailed p is
0.1217. Of course, also the relative risk is different: 0.7782 95%CI:
0.5736 - 1.0556 instead of: 0.76 (0.55 to 1.04) shown in Table 1. Furthermore, even if the secondary end points turned out to
be statistically significant in favour of the ECMO treatment (“the
relative risk of treatment failure, defined as death by day 60 in
patients in the ECMO group and as crossover to ECMO or death
in patients in the control group, was 0.62 with 95% Confidence
Interval of: 0.47 to 0.82; P<0.001, for example), the authors had
to sadly and sharply write that: “In conclusion, the analysis of the
primary end point … showed no significant benefit of early ECMO,
as compared with a strategy of conventional mechanical ventilation,
which included crossover to ECMO (used by 28% of the patients
in the control group).” The impact of this result that, according to
the Evidence Based Medicine (EBM), does not allow to recommend
the ECMO treatment in these very severely ill patients is, of course,
very frustrating for the physicians working in the Intensive Care
Units. So, the question that arises almost spontaneously is whether
a difference of a few cents (4 or 2, depending on the statistical test
carried out and on the exact at the fourth decimal figure p-values
obtained) should be considered so relevant as to make such a
clinically important inconclusive. To this regards, it has to do some clarifications. Firstly, it is
often misunderstood that the statistical significance threshold of
0.05 has to be always considered, in the clinical trials settings as
two-tailed, and, consequently the significance threshold is of 0.025;
so the difference is of 65 or 45 thousandths since the statistical
significance in the paper [64] has been reported only at the second
decimal figure. In any case, if the statistical significance threshold
had been settled at 0.10 during the planning of the study, would not
have had the current problems in the interpretation of its results
and in accepting an innovative strategy of treatment. Secondly, it
has to critically reconsider the rigid position of the regulatory
authorities to judge a controlled clinical trial as inconclusive
if the primary outcome has not been demonstrated by means
of a statistically significant result. Even if this position can be
considered as justifiable for trials aimed to a drug registration
for its commercialization, I think that it has to be assumed a more
flexible attitude in the case of a treatment such as the ECMO in the
Intensive Care settings. Indeed, it has also to consider: a) The clinical context in which the trial has been carried
out; b) The potential for care of the current treatment;
c) The methodological statistical aspects such as the real
difficulties in doing a direct and easy comparison owing to
the crossover from the control to the experimental group (or,
generally, a crossover even for both the treatment groups); d) The limitations of the trial that have been clearly and
exhaustively reported by Combes et al. [64] at the end of the
paper; and, lastly, e) Some pitfalls in the planning of the controlled clinical
trials those subsequent amendments (this trial had as many as
ten amendments) try to fix more or less successfully and the
remarkable duration of the trial that was approved in 2010
and is published 8 years after. So, I think that it is possible
to consider the trial as adequately supportive of the ECMO
treatment [65,66]. The recent proposal of moving down to 0.005 the statistical
significance threshold is, of course, well-motivated in the Benjamin
et al. [1] and also in the previous paper from Johnson [13]. However,
it has to say that accepting such a proposal is involves such a
change in the scientific world, in the mentality of researchers, in
drug development by the pharmaceutical companies that could
have negative consequences at least in the first years following.
I think that it is mandatory that researchers have an adequate
knowledge of the statistical method and also of the meaning of
the p-values in order to appropriately consider the results of the
research and to be absolutely aware of their use. One could begin
to request that p-values be accompanied by considerations about
the probability that the null hypothesis (and / or the alternative) is
true. These considerations should have an appropriate prominence
perhaps even in the context of the conclusions of the abstract of the
published papers.P-values: Some Historical Considerations
The meaning of the p-values
Bayes Factors
The case of a greater significance level
The sample sizes aspect
An intriguing case
Conclusion
References


