Sliding Fractal Dimensions of Subviral Particles in Fluorescence Image Sequences Volume 6 - Issue 2

Andreas Rausch*and Thomas Schanze

• Technische Hochschule Mittelhessen (THM), FB Life Science Engineering (LSE), Institut für Biomedizinische Technik (IBMT), Germany

Received: June 19, 2018;   Published: July 05, 2018

*Corresponding author: Andreas Rausch, Technische Hochschule Mittelhessen (THM), FB Life Science Engineering (LSE), Institut für iomedizinische Technik (IBMT), Wiesenstrase 14, Germany

DOI: 10.26717/BJSTR.2018.06.001338

Abstract PDF

The research for new medicines against pathogens of hemorrhagic fevers like the Ebola or Marburg virus is a work intensive field in pharmaceutical science. It requires an accurate knowledge of the pathogens’ behaviors to assess the influences of new potential medicines on them. In cooperation between the Virology of the Philipps-University in Marburg and the Institute for Biomedical Engineering at the University for Applied Science in Gießen new algorithms for automatic detection and classification of subviral particles in fluorescence image sequences were introduced. In this article a new method to analyze and classify the temporal variations of motion patterns of subviral particles is presented. The fractal dimensions within sliding time windows reveal the dynamic changes of the particles motion-steadiness. This allows making statements about time dependent influences of unknown substances to infected cells. This article describes the new method and delivers a proof of concept. First results on real data show a good potential of this method to assist pharmaceutical research. The article ends with a discussion and conclusion.

Keywords: Subviral Particles; Particle Tracking; Fluorescence Images; Fractal Dimensions

The accurate knowledge of the behaviors of subviral particles in fluorescence image sequences is elementary for pharmaceutical research. For this a new imaging method to observe infected flat cells was established [1]. Additionally, a tracking algorithm to automate the detection and thus reduce the evaluation effort was introduced recently [2,3]. For the pharmaceutical researchers it is highly important to have access to easy and fast classification measures. Besides the particles amount, sizes or density deviation in infected cells also the motion patterns provide important information about their properties. While this not only includes the particles velocities and directions a method to describe the steadiness of their motion using fractal dimension-determination was developed [4]. This only allows to describe and classify the motion pattern of subviral particles within a whole sequence. Thus, the temporal information is lost. In this article a new method to analyze the temporal development of sub viral particles motion patterns during a sequence using fractal dimensions-determination via box counting is introduced. This promises to enable new possibilities for the investigation of subviral particles

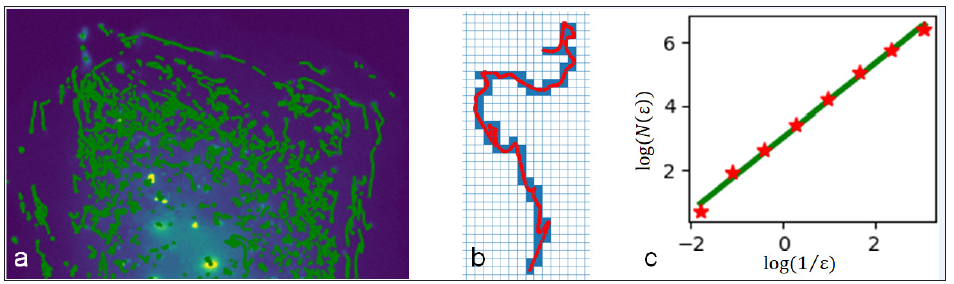
Classical motion patterns of particles like velocity and direction can be easily obtained and assessed. Of course, there is much more information hidden in the tracks. The motion pattern of a subviral particle can be complex, in addition, their movements vary individually and can be non-stationary. It is observable that in all sequences a certain amount of the particles shows a quite simple behavior, e.g. a directed motion pattern, while others appear to be chaotic. But to just assess their mean behavior is not sufficient. A measure that takes into account temporal changes is required. The previously introduced Kienzle- and LAP-Kalman-algorithms provide lists of coordinates representing the spatio-temporal positions of all automatically detected particles in an image sequence [2,3]. An exemplary extract of a maximum projection image of a real sequence with particle tracks is shown in Figure 1a. Based on this information the temporal fractal dimensions of the subviral particle trajectories can be determined. Fractal dimensions can be used to describe the complexity of any object of any dimension. A prominent example is the determination of coast lengths [4]. In our case the track coordinates are interpolated by cubic splines, in order to meet the physics of moving particles, i.e. no jumps in acceleration. As we are observing flat cells the “trajectories” are present in a twodimensional domain. Thus, the fractal dimension of a subviral track at any time is naively expected to lie in the interval between 1 (a straight, one-dimensional line) and 2 (a highly chaotic, plane-filling track). The range of fractal dimensions of real subviral particles is often a bit larger than one [5]. The particles’ fractal dimensions are measured using box-counting [6], described with

while N is the amount of boxes, laid onto the image and passed by the track and ε is the current edge length of boxes. The principle of box-counting is visualized in Figures 1b & 1c. To reveal the variability of a track’s fractal dimension and thus its motion steadiness, the box-counting is applied within a sliding time window. The window size is set to 12 frames (rate: 1 frame⁄sec).

Figure 1: Method: (a) the sub viral particles in an image sequence of an infected flat cell were tracked (green). (b) The boxes (blue) passed by a track (red) are counted for box-counting. (c) The slope of the relationship between the number of passed boxes and the boxes edge-length equals the fractal dimension (slope of green regression).

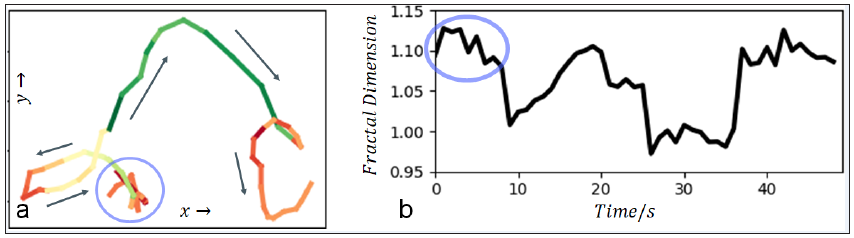
To show the potential of the new method ten-realsub viral particle tracks with different temporal motion patterns were selected for analysis. One exemplary track is shown in Figure 2a. The tracks motion pattern goes from complex (chaotic), to quite directed and to complex again. The box-counting was applied with a sliding window. The progress of the fractal dimensions is shown in Figure 2b. To visualize the temporal fractal dimensions the track in Figure 2a is color-coded with green-, red- and yellow-tones for directed, more complex and, potentially, chaotic phases of motion. Other tested tracks yielded equivalent results. We found a span of fractal dimensions from 0.92 to 1.18 with a mean of 1.02 and standard deviation of 0.05.

Note: Due to uncertainties related to sampling or to a standstill of a particle, the dimension may be temporally less than one.

Figure 2: Results: (a) Track with temporal varying motion pattern is shown. The running direction is marked with arrows. The temporal measured fractal dimension is color coded (green – low, yellow – moderate, red – high). (b) The sliding fractal dimension of the track in (a) is shown. The light-blue ellipse marks a region of high fractal dimension, corresponding to the ellipse in (a).

A sliding fractal dimension analysis to classify motion patterns of subviral particles was introduced. First results promise good potential to assist the pharmaceutical researchers in observing the dynamic processes in normal and infected cells. An improvement of the algorithm to handle quasi-still stands of particles must, like a statistical evaluation, be addressed in future work

1. Schudt G, Klesnikova L, Dolnik O, Sodeik B, Becker S (2013) Live-cell imageing of Marburg virus-infected cells uncovers actin-dependent transport of nucleocapsids over long distances. Proc Nat Accad Sci USA 110(35): 14402-14407.
2. Kienzle C, Schudt G, Becker S, Schanze T (2014) Multiple Subviral Particle in Fluorescence Microscopy Sequences. BVM Springer Verlag A pp. 330-335.
3. Rausch A, Müller D, Schanze T (2016) Improvement of a Subviral Particle Tracker by the Use of a LAP-Kalman-Algorithm. CDBME 2(1).
4. Mandelbrot B (1967) How long is the coast of Britain Statistical selfsimilarity and fractal dimension. Science 156(3375): 636-638.
5. Rausch A, Schanze T (2018) Fractal Dimensions of Subviral Particle Movement. CDBME 4.
6. Annadhason A (2012) Methods of fractal dimension computation. IJCSITS 2(1): 2249.