On Filtration in a Rectangular Interchange with A Particularly Unpermatable Vertical Wall in the Evaporation Volume 5 - Issue 1

EN Bereslavskii* and LM Dudina

• St. Petersburg State of Civil Aviation Univerity, Russian Federation

Received: May 24, 2018;   Published: May 30, 2018

*Corresponding author: EN Bereslavskii, St. Petersburg State of Civil Aviation Univerity, 38, Pilots street, St. Petersburg, Russian Federation

DOI: 10.26717/BJSTR.2018.05.001145

Abstract PDF

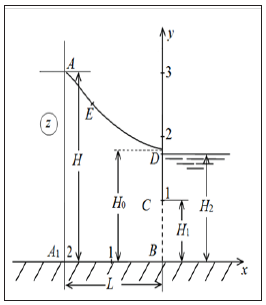
In Figure 1 the rectangular crossing point with slopes of AA1 and DB on the impenetrable horizontal basis of length of L is presented. Water height in the top tail of Н, lower tail with water level of Н2, having partially impenetrable vertical wall CD (screen), adjoins a layer sole. If the working part of the crossing point CB (filter) of width of H1 is flooded, H2>H1, an interval of seepage, usual for dams, is absent. The upper bound of area of the movement is the free surface of AD, coming to the disproportionate CD, screen to which there is a uniform evaporation of intensity ε (0 < ε < 1). Soil is considered uniform and isotropic, the current of liquid submits to Darci law with known coefficient of a filtration κ = const.

Figure 1: Picture of a current in a rectangular crossing point calculated at ε = 0.5, H = 3, L = 2, H1 = 1, H2 = 1.4.

We will enter the complex potential of the movement ω =ϕ + iψ (φ – speed potential, ψ – function of current) and complex coordinates z=x+ iy, carried respectively κH and H, where H – a pressure in A point. The task consists in definition of provision of a free surface of AD and finding of ordinate of H0 – points of an exit of a curve depression to the impenetrable screen, and also a filtration expense of Q. We will enter: auxiliary area t (Figure 2) – semi-strip Ret > 0, 0 < Imt < 0.5π a parametrical variable t at compliance of points t_A = ∞ t_A1 = arcth ,√a1+0.5π,t_B= arcth ,√b1+0.5πi(1< a₁ < b < ∞),a₁ b – unknown affixes of points A1 and B in the plane t, tC =0.5πi and tD =0; function z (t), conformally displaying a plane t semi-strip on area z, and also derivative dω / dt и dz / dt.

Figure 2:

where М>0 – a large-scale constant of modeling. It is possible to check that functions meet the boundary conditions reformulated in terms of the dω / dt и dz / dt, functions and, thus, are the parametrical solution of an initial regional task. Record of representations for different sites of border of a semi-strip with the subsequent integration on all contours of auxiliary area of the parametrical t leads to short circuit of area of a current and, thereby, serves as control of calculations. The technique of creation of the exact ana lytical solution of a task on the movement in liquid in a rectangular crossing point with the screen in the presence of evaporation from a free surface of ground waters is developed. It is shown that the current picture near the impenetrable screen significantly depends not only on the filter size, but also on evaporation existence that is strongly reflected in an expense and ordinate of a point of an exit of a curve depression to the screen. The received results give an idea (at least qualitatively) of possible dependence of characteristics of a current by consideration of a task about a filtration already to an imperfect well or a tubular well.