info@biomedres.us
+1 (502) 904-2126
One Westbrook Corporate Center, Suite 300, Westchester, IL 60154, USA
Site Map
ISSN: 2574 -1241
ISSN: 2574 -1241
Received: May 14, 2018; Published: May 24, 2018
*Corresponding author: HY Wang, Institute P’, Fluides-Thermique-Combustion, CNRS, ENSMA, University de Poitiers, BP 40109, F86961, Futuroscope Chasseneuil Cedex, France
DOI: 10.26717/BJSTR.2018.04.001109
The phenomenological analysis of backdraft, experimentally observed in enclosure fire, has been made with the help of CFD simulation. The current numerical simulations include the initial mixing as a gravity current after opening of the enclosure, the ignition, spreading of flame in the enclosure, the external fireball, and subsequent decay. Histories of the calculated relative pressure pulse and temperature peak are compared with the measured ones. The predicted pressure and temperature levels agree quantitatively with the experimental data. Globally, Large Eddy Simulation combined with an EDC combustion model shows the feasibility for simulations of transient combustion events occurring in an enclosure filled with a mixture of fuel in air.
Keywords: Fire models, Toxic product, Heat flux, Enclosure fir, Backdraft
Complexes structures in many buildings lead to a new risks for human life and building. When a fire occurs in an under ventilated enclosure, during its initial phase, the fire growths as long as it is fuel-controlled. Then the fire can become limited by the available oxygen and large amounts of unburned fuel gases can be generated from a condensed fuel on a scale where the heat flux is significant. As more fuel exists in an enclosure, after a fire is extinguished, or reduced in intensity by oxygen starvation, the internal fire enters the decay phase, and the flame exhaust takes place. The mixing of these gases with oxygen can create a flammable mixture resulting in ignition and an explosive or a rapid combustion, referred to as backdraft. Thus backdraft is causecd by the subsequent introduction of fresh oxygen from an opening. Intensive research has been carried over decades on the enclosure fire dynamics [1-6], though only a small proportion of the work has looked specifically on the backdraft phenomenon [7-9]. The numerical work of Sinai [6] showed leakages and heat loss from wall have a major effect on stratification for an under-ventilated enclosure from a liquid pool fire. The numerical results of Yang [7] from a small-scale enclosure gave a comprehensive illustration of the phenomenon although without the comparison to the experimental data. Previous work [8] on CFD simulation of backdraft shows an over prediction of the temperature peak and pressure pulse by using one reaction step without radiation loss. The flammability range and ignition temperature are essential of the backdraft phenomena [9,10] depending on the fuel/air mixture.
The present study is motivated by fire safety questions following the accidental release of different fuel gases and possible subsequent ignition of a fuel/air mixture in an enclosure. In the Fire Dynamics Simulator (FDS6) code [11], based on a mixing-controlled combustion model, soot production is derived from the fraction of the fuel mass that is converted into soot, in addition to a radiative loss fraction. All these parameters can be specified for well-ventilated fires for adjusting the species and flame temperature, but not for a highly confined enclosure fire. A fire model’s treatment of soot formation has a profound influence on reliably predictions of mass burning of condensed fuels, flame spread and fire growth through thermal radiation. Moreover, for an accurate prediction of an ignition hazard, an extremely small grid size (mm) is required to solve the conservation equations and hundreds of species. Therefore, to make the problem computationally tractable, the subgrid scale mixing- controlled combustion via two chemical reaction steps and a global soot formation model are incorporated into FDS.
This allows to minimize the computational expense and, an adequate resolution of a full-scale enclosure fire can be achieved with a large spatial resolution. Predictions are provided of the transient heat release rate, mass flow rate and thermal/dynamic fields at various fuel gases conventionally used in industry comprise, such as methane, ethylene and propane. Comparison between the prediction and experiment shows that this entirely tractable solution gives sufficiently accurate predictions on the temperature, velocity and smoke concentration in a reduced scale enclosure fire. The outcome for estimating the risk of backdraft and the time between the opening of an enclosure and the triggering of a backdraft is encouraging. Overall, the comparison between numerical results and experimental data ranges from fair for ignition time to good for pressure pulse or temperature peak, and confirms the feasibility of a numerical treatment of backdraft phenomena.
This section outlines the physico-mathematical models invoked for the computations. The basis of the analysis is the conservation equations of mass, momentum, energy and species, a set of three-dimensional elliptic, time-dependent Navier-Stokes equations. These equations are the mathematical representation of the reacting flow phenomena of interest here. Turbulence is modelled using a standard Smagorinsky sub-grid scale model in a Large Eddy Simulation [11]. The finite-difference technique is used to discretize the partial differential equations. The precise formulation of the differential equations describing the model and the numerical technique can be found elsewhere [11], and will not be repeated here.
The combustion model is based on an Eddy Dissipation Concept (EDC) [12], and briefly described here. The combustion processes are governed by the conservation equations for the mass fraction, Yi, of the six major chemical species, such as CmHn, O2, CO, CO2, H2O and N2. The mixing-controlled combustion via two chemical reaction steps for CO formation, is assumed.
The combustion rate occurring at resolved scales is therefore controlled by the eddy mixing rate with which the local reaction rates of fuel and CO, are calculated from an EDC [12].
where s denotes the stoichiometric coefficient, and Yi the fuel/ CO mass fractions. The source term is multiplied by Heav(T-Tign), where Heav is the Heaviside unit step function, which is zero when its argument is negative (T<Tign and Yfuel flammability range) and 1 when it is positive (T>Tign and Yfuel flammability range). This simple ignition model allows to initiate the combustion process, when conditions near the heat source reach the flammable range for a given fuel. In the numerical calculation, the ignition time is computed automatically, and marks reaching the flammability limit at the ignition point thus triggring the ignition algorithm. The key timescales , can be related approximately to the resolved dissipation rate.
In the present study, we apply the dynamic modelling method to obtain appropriate value of the EDC coefficient.
where is the fraction of the fluid contained within the fine structures.
Here is a factor between zero and one to express the fraction of the fine structures which can react as a function of the mixture fraction, Z.
and
where Zst is the stoichiometric mixture fraction. The dynamic modelling method in terms of k, and the kinematic viscosity , allows to take into account the mass transfer rate between the fine structures and the bulk of the fluid. The subgrid scale dissipation rate, , in a LES calculation, can be derived from the resolved scale strain rate tensor, Sij .
where Zst is the stoichiometric mixture fraction. The dynamic modelling method in terms of k, and the kinematic viscosity , allows to take into account the mass transfer rate between the fine structures and the bulk of the fluid. The subgrid scale dissipation rate, , in a LES calculation, can be derived from the resolved scale strain rate tensor, Sij.
Here is the eddy viscosity from the analysis of Smagorinsky [11]. The turbulent kinetic energy, k, is obtained through a length on the order of the size of a grid cell, Δ , as follows:
Finally, the heat release rate is determined from the consumption rate of the two combustibles of CO and CmHn.
Soot is the dominant influence on the absorption coefficient in large fires, and it has been established that the majority of the radiation in fire plume (>90%) is derived from the visible part of the flame, where soot particles are radiating heat. For this, a radiative transfer equation is solved [11], and the effect of soot concentration on radiation is included by adding the radiation coefficient of soot into that of gas. However, soot production in fire plumes is a highly complex subject due to the spatially-varying formation and oxidation processes, the influence of turbulent fluctuations and strong temperature and fuel dependent effects. Nevertheless, a number of researchers [13] have had some success in identifying factors which allow simplified analysis. The current model use classic principle of smoke point to relate soot production to material properties. A fuel’s smoke point is the maximum height of its laminar flame burning in air at which soot is not released from the flame tip. A global soot formation model is incorporated into a turbulent flow calculation in a convection-diffusion equation for the soot mass fraction.
The soot production rate is written as:
Two mixture fraction limits delimit the soot formation and oxidation regions. The incipient mixture fraction is Zc=0.15, and the mixture fraction threshold where soot oxidation starts is Zso=0.1. Based on a LSP (Laminar Smoke Point) concept [13], soot formation is assumed to be controlled by second-order homogeneous gaseous reaction processes, and thus, is expressed as a function of the mixture fraction, Z, and gas temperature, T:
Here the temperature exponent γ = 2.25 and activation temperature are assigned. The parameter for differences in sooting behaviour of different fuels is the pre-exponential factor, If, which is reversely proportional to its LSP height without establishing fuel- specific model constants. From the smoke point height measured for many fuels [13], If is determined as 1.5x10-5, 4x10-5 and 2.6 x10-5 for methane, ethylene and propane, respectively. Although this approximation is incapable of accurately reproducing soot surface growth, it should be capable of capturing global trends for use in engineering calculations of radiation and visibility from fires. The soot oxidation in Eq.(12) is assumed to proceed through a single reaction step,
C +O → CO2 (14)
The soot oxidation is considered as a surface-area dependent mechanism, and its rate is evaluated from an Arrhenuis expression for laminar flame [13]. In turbulent flame, there remain some approximations due to turbulence interactions. By assuming that the mixing time in sub-grid scale is the limiting mechanism, the specific rate of soot oxidation is expressed by an EDC approach [12].
Where denotes the stoichiometric coefficient for burning 1 kg soot. This model contains no chemically kinetic mechanism to suppress homogeneous soot formation by O2.
This approach to the field modeling of fire spread over an enclosure emphasizes high enough spatial and temporal resolution. Special care should be taken to construct numerical grids with sufficient resolution and uniformity. Simulations are performed on a multi-processor Linux cluster available at the Institut P’ of Poitiers, using the parallel MPI [11]. In an enclosure, a rapid combustion, referred to as backdraft, reveals a complicated multistage process, such as internal burning before flame exhaust and external burning after flame exhaust. A large-scale under ventilated enclosure fire is difficult to analyze experimentally because duration of the multistage process is always too short (2 – 5 seconds). Therefore, the reduced scale enclosure fire which was examined experimentally by NIST [4], is first chosen for evaluation of the current numerical model.
The coordinate system and the enclosure geometry [4] (H=1 m, W=1 m and L=1.4 m) are shown in Figure 1. The experimental setup box is 1/3 of the standard ISO room with a doorway of h=0.8 m in height and of w=0.5 m in width. A horizontal square burner with an area of m2 was mounted on a floor level at the centre of the enclosure, allowing burning of the fuel as heptane. The wall, ceiling and floor were constructed from an insulating material. In the numerical simulations, an extended region measuring 2 m x 1.2 m in plane x-y, and 1.6 m in height (z) is used. For this enclosure fire, an adequate resolution of the fire plume can be achieved with a spatial resolution of about 4 cm from an uniform grid system containing 50(x) x 30(y) x 40(z). CPU times were of the order of 5 days for a real 75 minutes simulation in transient mode. Even for such enclosure fire in reduced scale, there are still very few experimental data available due to the high cost and the instrumentation difficulty. The temperature, the volume fraction of the chemical species as O2/CO2 and the soot mass fraction are measured in transient mode only in two points through the probes close to the front door and the rear wall. Five probes are also vertically placed on the centreline of the front door to measure the normal velocity at a height of 5, 20, 40, 60 and 80 cm above the floor.
Figure 1: Coordinate system and the enclosure geometry with a horizontal square burner.
In the experiments [4], the opening size was fixed and the equivalence ratio was varied by changing the mass flow rate of the fuel, giving a theoretical heat release rate (HRR) varying from 80 to 350 kW. The maximum theoretical HRR inside the enclosure can be derived by multiplying the ventilation controlled mass inflow of air by the energy released per kilogram of air completely consumed inside. For such enclosure fire, the peak in theoretical HRR calculated from Qmax=3000x0.5Ah1/2 (kW) [3] where A (m2) and h (m) are area and height of the doorway respectively, is equal to 530 kW. As an illustration, evolution of the calculated HRR by using the measured mass loss rate of the fuel is compared with the theoretical one in Figure 2. Such enclosure fire is ensured by abundant oxygen from air entrainment at the doorway because the heat release rate is below 530 kW, and as a consequence, the calculated HRRs from FDS6 and the current model approach the theoretical one, implying a practically complete combustion. A progressive increase of the heat release rate is characterized by a development of external burning due to fire extent growth. The flame propagation is analysed by examining the contours of the temperature (Figure 3).
Figure 2: Evolution with time of the theoretical and calculated Heat Release Rate.
Figure 3: Contours of the temperature (°C) at the external burning stage.
Figure 4: Temperature at the front probe as a function of the heat release rate.
According to the experiment [14], for a heavily sooting flame, the visible flame shape corresponds to the zone where the gas temperature higher than 500°C and this criterion is used for determining the predicted flame shape. There is quasi-steady split burning characterized by the two regions of the flame, one inside the box near the fuel source, and the other one outside the box. The temperature at the front probe versus the HRR during the fire is presented in Figure 4. When the HRR is small, the flame is attached to the burner base, corresponding to fuel controlled fire, and the hottest gases with a temperature level of 500°C from the combustion products are ejected through the opening. Globally, the temperature continues to increase steadily up to 1200°C with the HRR due to increase in the flame size until it attains a quasi-steady state once the external flame takes place. The predicted temperature trend from both FDS6 and the current model versus the HRR is consistent with the measured one [4].
The normal velocities measured and predicted from FDS6 and the current model near the doorway from the vertical probes for the HRR of 80 and 300 kW are plotted in Figure 5. Both the prediction and measurement indicate that the processes of air entrainment into the enclosure are enhanced with an increase of the HRR through a buoyant vertical acceleration of the thermal plume and formation of a ceiling jet in the enclosure, which later spills over the opening. A stratified two layer flow in the opening region is numerically reproduced, and the position of the neutral plane is well distinguished. This implies that the enclosure is only partly filled with hot gases, collected under the ceiling, and the temperature forms a two-layer profile. Air is being entrained into the enclosure only from one half of the opening area and the hotter gas is ejected through the upper part of the opening due to the thermal expansion. The peak in the velocity of the entrained air at lower part of the opening is approximately 1 m/s, practically independent of the heat release rate. While the peak in the velocity of the ejected hotter gas from the upper part of the opening increases from 3 to 6 m/s with an increase of the HRR from 80 to 300 kW. It seems that the ejected mass flow rate from the enclosure is in terms not only of the opening geometry, but also of the complicated multistage process of an enclosure fire. A simple expression [3], which is based only on the opening area to specify the mass rate of air inflow, may not be appropriated.
Figure 5: Normal velocity of the entrained air at the doorway for HRRs of 80 and 300 kW.
The transient histories of the oxygen, CO2 molar fraction and soot mass fraction at the front and rear probes are respectively presented in Figures 6-9. A relatively good agreement between the prediction from FDS6/the current model and the experiment for the examined chemical species as O2 and CO2 is observed. The calculated oxygen mole fraction presents the oscillations with time mainly due to the coherent periodic oscillations of the flame arising from air entrainment in a cyclic manner due to buoyancy. At the initial fire growth stage, the flame is attached to the burner base, corresponding to fuel controlled fire, and there is sufficient oxygen available for the CO oxidation into CO2. The oxygen starvation begins and the oxygen-lean, fuel-rich hot upper layer is being formed due to the excessive pyrolysis products near the fire source. Amplitudes of the CO2 production vary strongly from one cycle to another, and their maximum levels increase with the heat release rate due to development of the external flame. The reactants dilute in the enclosure, and this is accompanied by a rapid rise of the soot level at the rear wall due to increase in the equivalence ratio. Evolution of the soot formation with HRR is practically reproduced by the current soot model. However, in the fuel-rich condition, soot production is significantly over-predicted by using FDS6 due to lack of the soot oxidation process.
Figure 6: History of the oxygen volume fraction at the front probe.
Figure 7: History of the oxygen volume fraction at the rear probe.
Figure 8: History of the carbon dioxide volume fraction at the rear probe.
Figure 9: History of the soot mass fraction at the rear probe.
In the following section, one of the full-scale backdraft experiments conducted at Lund University [9] is simulated by using the current model. The geometry of the enclosure considered here is 5.5 m long, 2.2 m high and 2.2 m wide. The opening was located in the middle of the enclosure, covering the full width and one-third of the enclosure height. The wall, ceiling and floor were constructed from an insulating material. In the numerical simulations of such enclosure fire, an extended region measured 14 m long, 6 m deep and 7 m high is used for capturing the venting of burned gas, the external combustion. For this enclosure fire, an adequate resolution of the fire plume can be achieved with a spatial resolution of about 5 cm from an uniform grid system.
Figure 10: Distribution of CH4 before ignition.
Backdraft reveals a complicated multistage process, such as the initial mixing as a gravity current after opening of an enclosure, the ignition, spreading of flame in the enclosure, the external fireball, and subsequent decay. Initially, the enclosure is filled with a mixture that contains CH4 with a masse fraction of 0.35, air of 0.3 and combustion products of 0.35. A liner vertical temperature profile varying from 107°C at the ceiling to 20°C was prescribed inside the enclosure as measured in the experimental case [9] with an ambiant temperature of 5°C. In the numerical model, a thermal energy source was imposed temporarily at the back of the enclosure, and the fuel concentration is checked at each time step. Since temperature within the enclosure is significantly higher than the ambient one, the average enclosure density is below the ambient one. Once the enclosure is opened, flow may enter or leave depending on the local pressure just at the opening, as shown in Figures 10 & 11. The flow at the opening is developing, and a stream of fresh and cold air enters the enclosure, referred to as gravity current. A stratified two layer flow within the enclosure is formed, but at the initial stage, there is insufficient oxygen available and temperature level for triggring the ignition.
Figure 11: Distribution of temperature before ignition.
Following the mixing of the fresh air with the fuel-rich medium, concentrations return to the inflamability limit at the ignition sources, flaming combustion is initiated and develops into a deflagration. Figure 12 depicts an instantaneous view of the flame shape and smoke, obtained during the experiment from a video camera. After ignition, pulsating flame occurs as the oxygen starvation begins and the oxygen-lean fuel-rich hot upper layer is being formed. Burning has occurred in a lack of oxygen, more fuel exists in the enclosure than the air required for its combustion, the flame exhaust, said the ventilation-controlled fire occurs. The oxidizer is quickly consumed, the flame travels in the enclosure towards the opening in an opposite direction to the incoming air flow. Consequently, the excess combustible gases which serve as a burner, are strongly vented out of the enclosure where they burn on contact with the abundant ambient oxygen. In the numerical simulation, ignition is triggered at t=11.6 s by flammable conditions existing around a thermal energy source, and subsequently, the fire front is formed. As presented in Figure 13 for the gas temperature higher than 500°C, burning occurs not only inside the enclosure, but also outside, caused by the expulsion of the fuel gas from the enclosure upstream of the primary flame front. The CFD instantaneous temperature field after the ignition bears a good similarity to the measured one, and provides a reasonable guideline to the appearance, much more like a real fireball, as far as a video camera is concerned.
Figure 12: Instantaneous view of the experiment.
Figure 13: Instantaneous view of the predicted flame after ignition at t=11.6 s.
Figure 14: History of the temperature at the opening after ignition.
Figure 15: History of the relative pressure at the opening after ignition.
Temperature and pressure were measured in transient mode only in one point through the probes close to the front opening [9]. Histories of the calculated temperature and relative pressure (P-P0) are compared with the measured ones in Figures 14 & 15. Positive values indicate an overpressure at the opening, and negative values a depression. This simulation is to model fire spreading through the mixture of fuel, air and combustion products from the time at which an opening occurs. The time interval between temperature measurements [9] is too long, and consequently, the natural constraints imposed by the slow frequency response of the instrumentation prevent complete validation of this model. Previous work [8] on CFD simulation of backdraft used a single reaction step without radiation loss, resulting in an over prediction of temperature peak and pressure pulse, with almost a factor of 2 greater than the measured data. The greatest source of scatter for the prediction of the amplitudes of the temperature and pressure originates from the inherent complexity in chemical reaction during the multistage process of the enclosure fire. The present work is based on a twostep combustion model in addition to the radiation loss. The good agreement when comparing the pressure pulse or temperature peak with the experimental data suggests that the total amount of fuel mass consumed within the enclosure is reasonably well predicted via two chemical reaction steps.
In the experiments [9], the ignition time is about 35 s determined by visual identification of fire. The calculated ignition point is reached at the time of 11.6 s, which is smaller than the ignition time observed in the experiments. Difference between the simulation and the data for the ignition time is greater, suggesting that the rate of combustion during the ignition stage is predicted less accurately. Besides, the difference may partly be due to different identification of the ignition event. The predicted instantaneous field of velocity vectors after the ignition at t=11.6 s is presented in Figure 16. As the air reflects from the back wall, a large premixed region is created, where the mixture is within the flammability limits.
Figure 16: Instantaneous view of the predicted velocity vectors after ignition.
Figure 17: History of the ejected mass flow rate for the different fuel gases.
The processes of air entrainment into the enclosure are enhanced with an increase of the HRR through a buoyant vertical acceleration of the plume. The hotter gas from the combustion products is ejected through the opening due to the thermal expansion. The expanding products of combustion accelerate the flow from the enclosure to the external environment. The speed of the ejected hotter gas from the opening approaches a value of 30 m/s. The deflagration expels fuel-rich mixture into environment, and the combustion continues outside the enclosure, as illustrated in Figure 13. The mass flow rates in and out of the enclosure are in terms of not only the opening geometry, but also the complicated multistage process of an enclosure fire. Figure 17 compare histories of the outflow mass flow rate for the three fuel gases which have its flammability range [10], given as 0.05<YCH4<0.15, 0.027<YC2H4<0.36 and 0.021<YC3H8<0.095. A global ignition temperature with a value of 640°C, 449°C and 500°C has been adopted for methane, ethylene and propane, respectively. As shown in Figure 18, after opening at approximately 4s, the inflow can be assumed to be quasi-steady with a total mass flow rate of 0.4 kg/s into the enclosure.
Figure 18: History of the mass flow rate towards the enclosure for the different fuel gases.
Figure 19: History of the relative pressure after ignition for the different fuel gases.
After ignition, combustion continues close to rich limit of flammability in a vitiated enclosure. The flame increases rapidly in size, and the oxidizer inside the enclosure is quickly consumed. Then the flame travels in the enclosure towards the opening in an opposite direction to the incoming air flow. During this stage, the hotter gas is pushed outside of the enclosure with a mass flow rate of about 15 kg/s, preventing the fresh air entry due to the overpressure in the enclosure. The mass flow rate of the incoming air (Figure 18) reaches up to 2 kg/s just after the flame traveling towards the opening due to the depression there. The driving flow into the enclosure continues long after the inside flame has subsided, resulting of the thermal energy stored in the enclosure. As illustrated in Figure 19, evolution of the pressure with time bears a similarity for the three fuel gases. The simulations provide valuable insights into the effects of fuel type on the magnitude of the depression pulse. Ethyl-ene induces the highest magnitude of the depression, implying the strongest inflow towards the enclosure.
The simulated ignition time depends strongly on the imposed ignition temperature level, and is shorter with a low level of the ignition point. In fact, the combustion dynamics including the ignition, spreading of flame in the enclosure and the external fireball remain quite complex since they depend strongly on the reaction kinetics. It seems that the current combustion model only takes into account state of the fuel-air mixture field found at ignition point. So the numerical results are qualitatively promising. As an illustration, the calculated time distributions of heat release rate (HRR) for the three fuel gases are examined in Figure 20. The simulations provide insights into the transient combustion dynamics that follow ignition depending on the fuel type. The calculated HRR presents a similar trend during the combustion process initiated over the enclosure. The mixing process of various fuel gases with air results in different portions of the fuel vapor cloud being within the fuel-air flammability limits.
Figure 20: History of the heat release rate during backdraft for the different fuel gases.
Figure 21: History of the ejected heat flow rate towards the environment for the different fuel gases.
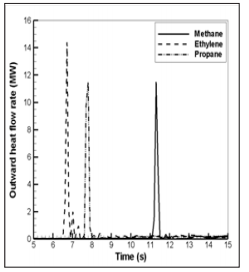
The difference from the fuel gases density in the initial mixing as a gravity current which precedes a backdraft affects the HRR level. The HRR reaches a maximum shortly after ignition (at t=7 s for C2H4, at t=8 s for C3H8 and at 11.6 s for CH4) and its peak value ranges from 120 MW for C3H8 to 160 MW for C2H4 and CH4. In all the cases, the combustion phase is short and lasts between 1.5 and 2 s; combustion ceases because of fuel depletion. The magnitude of the pressure pulse or temperature peak is correctly predicted (Figures 14 & 15), which suggests that magnitude of the HRR might also be reasonably predicted. Figure 21 presents the time variations of the simulated heat flow rate of the ejected hotter gas with a peak of about 12 MW. That means that only 8-10% of the total HRR originates from the combustion products within the enclosure. The ejected fuel vapor cloud from the opening due to the thermal expansion is flammable fuel-rich and the leaving excess fuel then subsequently mixes with abundant ambient air. The combustion continues outside the enclosure and fire propagates across the flammable region, leading to the most intensive combustion as fireball (Figure 13).
Figure 22: History of the temperature at the enclosure centre after ignition for the different fuel.
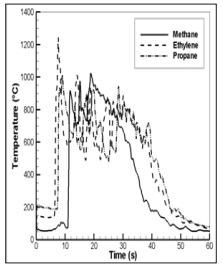
Figure 22 presents the time variations of the simulated temperature at the enclosure centre. During the fire front travelling inside the enclosure, the gas temperature level reaches a maximum of about 1000°C which is less sensitive to the fuel type. The temperature higher than 800°C is maintained even as the hotter gas has been pushed outside of the enclosure. A large recirculation flow due to inflow towards the enclosure lasts about 40 s. During this stage, the colder gases are entrained towards the enclosure, and the gas temperature rapidly decreases from 800 to 200°C. The temperature slowly diminish from 200°C to ambiance during about 20 s. Fire resistance of the building elements depends on the enclosure energy balance, which is greatly affected by heat transfer from the hot gases to the enclosure surfaces. During the flame travelling inside the enclosure, the fire front has a more pronounced impact on the ceiling through the radiation flux (Figure 23) and the convection flux (Figure 24). Flame radiation flux is computed from a discrete representation of the radiative intensity equation [11]. The Couette flow is assumed to prevail near the wall surface, and the convective heat feedback is calculated from a wall function.
Figure 23: Radiative heat flux along the ceiling during the flame ejection period for the different fuel gases.
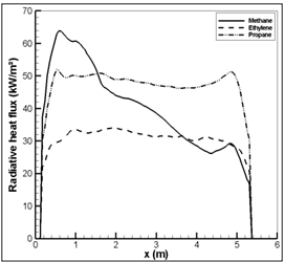
Figure 24: Convective heat flux along the ceiling during the flame ejection period for the different fuel gases.
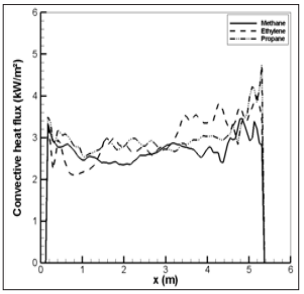
For CH4, the soot formation is relatively weak, and the peak in radiation flux is the most important. This induces a significant variation of the radiation flux near the ceiling from 60 to 30 kW/m2 by looking at the position from left to the right as the flame travels in the enclosure towards the opening. Distribution of the radiation flux is relatively uniform for C3H8 and C2H4 due to a strong soot formation favouring an uniform temperature distribution near the ceiling thanks to enhanced radiative heat transfer. The peak in radiation flux is the lowest for C2H4 due to the strongest soot formation which reduces the flame temperature level through radiation loss. For any fuel type, the convection flux is relatively uniform with about 3 kW/m2 (Figure 24) due to a large recirculation of the hotter gas inside the enclosure. The radiative fraction of the heat released by combustion is more than 90% of the total heat feedback which is transferred to the ceiling. It should be noted that the heat flux higher than 20 kW/m2 inside enclosure with temperature beyond 600°C during 40s (Figure 22) can potentially maintain the pyrolysis of the condensed fuel if it is exposed there. In this case, a combustible flux load will be still available in an enclosure, and the thermal radiation of the walls and the hotter gases potentially induces an ignition of fuel/air mixture exposed inside an enclosure.
The current fire model allows to obtaining sufficiently accurate predictions of thermal and dynamic fields to make CFD calculations of large-scale fire feasible in an engineering context. A good agreement was achieved for temperature, velocity and soot concentration profiles for a reduced scale enclosure fire. The behaviour of the highly transient structure of the enclosure fire is identified, which is thought to play a prominent part in the entrainment and mixing processes in fires. One of the factors affecting the reproducibility of the heat release rate in an enclosure filled with a mixture of fuel in air is the fuel type. The peak in heat flux to the enclosure wall for various fuel ranges from 30-60 kW/m2, and the contribution of radiation is higher than 90% of the total heat flux. The peak in heat flux to methane is about a factor of 2 increases of that to ethylene.
This model is capable of adequately describing the essential simultaneous phenomena occurring in an enclosure fire. Difference between the simulation and the data for the ignition time is probably attributable to shortcomings in the combustion model, which only barely takes into account the reaction kinetics. The work is continuing with the aim of improving the quality of the predictions. Future work should focus on different enclosure aspect ratios, smaller openings, and openings at the floor level. Measurements of temperature, velocity, heat fluxes and toxic product from a full-scale enclosure fire, would consolidate the new insight provided by the CFD activity.
Abstract
PDF
