Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Shipra Baluja*, Divyata Lava and Mehul Bhatt
Received: April 03, 2018; Published: April 23, 2018
*Corresponding author: Physical Chemistry Laboratory, Department of Chemistry,Saurashtra University, Rajkot-360005 (Gujarat), India
DOI: 10.26717/BJSTR.2018.04.000991
The dissociation constants of some synthesized tetrahydropyrimidine derivatives were determined potentiometrically at ionic strength of 0. 1 M in N, N-dimethyl formamide: water 60:40 (v/v)system at 303.15 K. It is observed that dissociation constant depends on the substituent groups present in the compounds.
Keywords: Dissociation constant; Tetrahydropyrimidine; DMF; Enthalpy; Entropy; Gibb's Energy
The acidic or basic strength of material can be highlighted by the dissociation constants. They are also known as acidity constant, ionization constant or formation constant.Dissociation constant is one of the important physicochemical parameter which provides critical information about drug properties such as solubility, lipophilicity, acidity [1], transport behaviour, bonding to receptors [2] and permeability [3]. Further, dissociation constant data is required for QSAR study [4,5]. Hence, the relationship between the acid dissociation constants and structure in drug design studies is important [6]. It also provides useful information about tautomeric equilibria [7,8], solvent-solute interactions [9] etc.Various methods have been developed for the measurement of dissociation constants, such as potentiometry including pH metry [10] spectrophotometry [11], conductometry [12], solubility measurements [13], cryoscopy [14], measurements of the rates of acid catalysed hydrolysis of esters [15], measurement of the relative distribution of an acid between two immiscible solvents [16], dissociation constant by capillary electrophoresis [17], NMR methods [18], feedback- based flow radiometry [19], interfacial Fourier transform infrared spectroscopy [20], etc. Further, in last few years dissociation constant of many substances such as[21-27] have been studied by various workers.In the present work, the dissociation constant of tetrahydropyrimidine compounds have studied in N, N- dimethyl formamide at 303.15K.
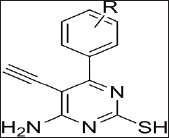
The Synthesized tetrahydropyrimidine derivatives are recrystallized. Figure 1 shows general structure of synthesized compounds.
Figure 1: General structure for tetrahydropyrimidine derivative.
Where R is:
SM-1: 4-OH, 3-OCH3-C6H4; SM-2: 4-OCH3-C6H4; SM-3: 4-OH-C6H4; SM-4: 4-C3l-C66H44;
SM-5: 3-Cl-C6H4; SM-6: 4-F-C6H4; SM-7: 3-NO2-C6H4; SM-8: -C6H5; SM-9: C4H3O;
SM-10: -CH=CH-C6H5.
For the dissociation study, all the chemicals used were of B.D.H Analar grade. All the solutions used for the titration are prepared using Mili-Q water. For the titration, different solutions of different concentrations were prepared. i.e.,nitricacid (1.0 M), sodium hydroxide (0.5 M), sodium nitrates (1.0 M). The Solutions of all the compounds were perepared in DMF and of 0.1 M concentration. Nitric acid and sodium hydroxide were standardized by titrating with 0.1 N NaOH and 0.05 M succinic acid solution respectively. The buffer solutions used for the calibration of pH meter were 0.05 M potassium hydrogen phthalate and 0.01 M Borax buffer.Calvin Bjerrum method [28] is used for the determination of dissociation constant. For this, two sets of mixtures were prepared for titration.
First set of solution contains 2 ml HNO3+ 4 ml water + 30 ml DMF + 4.0 ml NaNO3and second set of solution contains 2 ml HNO3+ 4 ml water + 28 ml DMF + 2.0 ml compound solution + 4.0 ml NaNO3.The total volume of each solution was 40.0 ml and dimethylformamide:water ratio was 60:40 (v/v).The abovementioned solutions were allowed to attain a constant temperature (303.15 K) and then titrated against standard NaOH solution under an inert atmosphere of nitrogen.A systronic pH meter (Model No. EQ 664) was used for the pH determination. The systronic glass electrode and a saturated calomel electrode were used as indicator and reference electrodes respectively. Before operation, the glass electrode was immersed in 0.1 M HCl for twenty minutes. Then, it was washed thoroughly with distilled water.Before measurement, the pH meter was calibrated with buffer solution of known pH.
From the above two titrations, two titration curves were obtained for each compound solution. From these curves, the average number of protons associated with compound ( ) can be calculated by Irring and Rossotti equation [29].
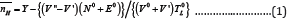
WhereY is the number of displaceable protons per compound molecule. V' and V" are the volume of alkali required at the same pH for both acid and compound titration curves respectively. V0 is the initial volume of the test solution. N0, E0 and T0Lare the initial concentration of the alkali, acid and compound respectively.For SM 1 and SM 3, value of Y is 2. Whereas for other compounds, Y is equal to one.
For all the compounds except SM-1 and SM-3 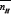 values are in between zero and one. For SM-1 and SM-3, nHvalue extends over the range from 0 to 2 indicating two dissociation steps. The values at = 0.5 were evaluated for each systemexcept SM-1 and SM-3. For these two compounds,
values are in between zero and one. For SM-1 and SM-3, nHvalue extends over the range from 0 to 2 indicating two dissociation steps. The values at = 0.5 were evaluated for each systemexcept SM-1 and SM-3. For these two compounds, 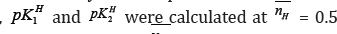 and
and 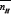 = 1.5. Figure 2 shows variation of
= 1.5. Figure 2 shows variation of 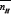 with pH (B) for SM-1 and SM-2.
with pH (B) for SM-1 and SM-2.
Further, the 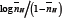 values are plotted against pH (B) for SM-1 is shown in Figure 3. The plot is a straight line from which
values are plotted against pH (B) for SM-1 is shown in Figure 3. The plot is a straight line from which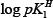 values were calculated at several pH (B) values, by the following equation:
values were calculated at several pH (B) values, by the following equation:
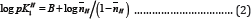
Figure 3: The plot of log nH/(2-nH) against pH (B) for [A] SM-1 and log nH/(1-nH) in against pH (B) for SM-2.
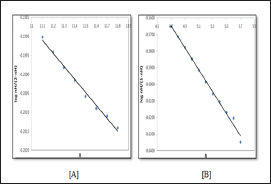
The average pk1H value is also reported in Table l.For all compounds. It is evident from tables that these pklHvalues are in agreement with that obtained by the Figure 2. i.e., at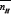 = 0.5.
= 0.5.
For SM-1 and SM-3, for all the points below 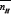 =1, the following equation was used.
=1, the following equation was used.
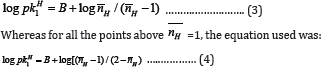
From the various values of log pKlH (or log pK2H) calculated for a system, the average value was calculated. The values of log pKlH and log pK2H calculated by these two methods i.e., half-integral method and average method are given in Table 1. It is observed that in most of the systems, the calculated values by these two methods are in good agreement.
Out of all systems studied, SM-1 and SM-3 are of H2L type whereas others are of HL type. Table 1 shows that the dissociation or acidic constant depends on the type of substituent groups present in the compound. Different groups interact differently with the solvent, which affect their dissociation.Comparison of pK1H values of compounds shows that, SM-5 is more acidic which contains m-chloro group. However, SM-8 is most basic which contains phenyl ring without substitution. SM-1 and SM-3 both contain hydroxyl groups at para positions. But, SM-1 is found to be more acidic than SM-3. From these results, it is concluded that different compounds exhibit different dissociation constant which also depends upon the type and position of substituent group.


