On One Aspect of Constrained Bayesian Method for Testing Directional Hypotheses Volume 2 - Issue 5

KJ Kachiashvili*

• Georgian Technical University, Faculty of Informatics and Control Systems, Georgia

Received: February 23, 2018;   Published: March 06, 2018

*Corresponding author: KJ Kachiashvili, Georgian Technical University, Faculty of Informatics and Control Systems, st. Kostava, Tbilisi, Georgia

DOI: 10.26717/BJSTR.2018.02.000821

Abstract PDF

The paper discusses the application of constrained Bayesian method (CBM) of testing the directional hypotheses. It is proved that decision rule of CBM restricts the mixed directional false discovery rate (mdFDR) and total Type III error rate as well.

Keywords: Cbm; Hypotheses Testing; Mixed Directional False Discovery Rate; Type Iii Error Rate

Directional hypotheses testing problem arises in many biomedical applications [1]. For parametrical models, the problem of testing directional hypotheses can be stated as H_o:θ = θ₀ vs. H_- :θ<θ₁ or H₊:θ>θ₀, where θ is the parameter of the model, θ₀ is known. A review of the works where the methods of testing the directional hypotheses are given can be found, for example, in [2,3]. Bayesian decision theoretical methodology for testing the directional hypotheses was developed and compared with the frequents method in [2]. While a new approach to the statistical hypotheses testing, called Constrained Bayesian Methods (CBM), was developed and applied alongside to other types of hypotheses to the directional hypotheses in [3]. One specific aspect of CBM for testing directional hypotheses, in particular, the fact that it restricts both the mixed directional false discovery rate (mdFDR) and total Type III error rate is proved below.

Let's denote: г₀ г_{_}, г₊ and are the regions of acceptance of the above-stated hypotheses ₀ , H_{_} and H₊ , respectively, and let us consider the following losses

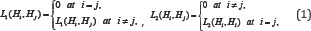
Where L₁(H_i,H_j) and L₂H_i,H_j) are the losses of incorrectly accepted and incorrectly rejected hypotheses. It is clear that the " 0-l" loss function is a private case of the step-wise loss (1). For loss functions (1), one of possible statement of CBM takes the form [3-5].

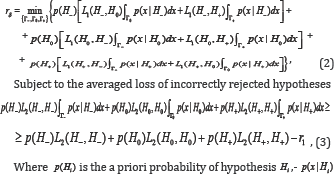
Denotes the marginal density of x given H_i , i.e. is a priori density with support 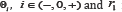is some real number determining the level of the averaged loss of incorrectly rejected hypothesis.

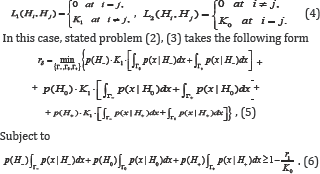
By solving constrained optimization problem (5), (6), using the Lagrange multiplier method, we obtain

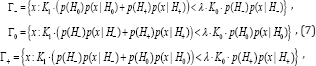
Where Lagrange multiplier λ is determined so that in [6] equality takes place. For optimality oftesting directional hypotheses, different concepts such as: mixed directional false discovery rate (mdFDR), directional false discovery rate (DFDR) and the Type III errors are offered in [1,6-10]. Let us consider mdFDR which is the exected proportion of falsely selecting H_- or H₊ . In our case, it has the following form

Theorem

When satisfying the condition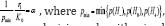 CBM with restriction level of [6] ensures a decision rule with mixed directional false discovery rate or with total Type III error rate less or equal to , i.e. with mdFDR = ERR^T_III + ERR^K_III ≤α .

Proof: Because of specificity of decision rules of CBM, alongside of hypotheses acceptance regions, the regions of impossibility of making a decision exist. Therefore, instead of the condition

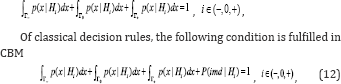
Where P(tmd| H_i) is the probability of impossibility of making a decision [3,11,12].

Taking into account [12], condition [6] can be rewritten as follows

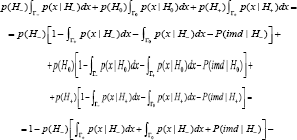
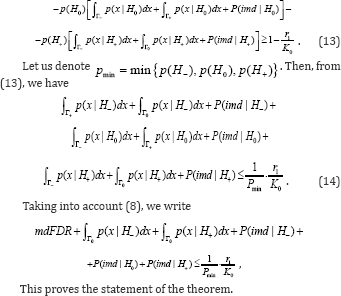
One more property of the optimality of CBM when testing the directional hypotheses is shown. In particular, when testing the directional hypotheses, the optimal decision rule of CBM restricts both the mixed directional false discovery rate [mdFDR] and total Type III error rate.

1. Bansal NK, Hamedani GG, Maadooliat M [2015] Testing Multiple Hypotheses with Skewed Alternatives. Biometrics 72[2]: 494-502.
2. Bansal NK, Sheng R [2010] Beyesian Decision Theoretic Approach to Hypothesis Problems with Skewed Alternatives. J of Statistical Planning and Inference 140: 2894-2903.
3. Kachiashvili KJ [2018] Constrained Bayesian Methods of Hypotheses Testing: A New Philosophy of Hypotheses Testing in Parallel and Sequential Experiments. Nova Science Publishers Inc p. 456.
4. Kachiashvili KJ, Hashmi MA, Mueed A [2012] Sensitivity Analysis of Classical and Conditional Bayesian Problems of Many Hypotheses Testing. Communications in Statistics-Theory and Methods 41[4]: 591605.
5. Kachiashvili KJ [2011] Investigation and Computation of Unconditional and Conditional Bayesian Problems of Hypothesis Testing. ARPN Journal of Systems and Software 1[2]: 47-59.
6. Shaffer JP [2002] Multiplicity, directional [Type III] errors, and the null hypothesis. Psychological Methods 7[3]: 356-369.
7. Benjamini Y, Yekutieli D [2005] False discovery rate: Adjusted multiple confidence intervals for selecting parameters. Journal of the American Statistical Association 100: 71-93.
8. Bansal NK, Miescke KJ [2013] A Bayesian decision theoretic approach to directional multiple hypotheses problems. J of Multivariate Analysis 120: 205-215.
9. Jones LV, Tukey JW (2000) A sensible formulation of the significance test. Psychological Methods 5[4]: 411-414.
10. Kaiser HF [1960] Directional statistical decisions. Psychological Review 67: 160-167.
11. Kachiashvili GK, Kachiashvili KJ, Mueed A (2012) Specific Features of Regions of Acceptance of Hypotheses in Conditional Bayesian Problems of Statistical Hypotheses Testing. Sankhya: The Indian J. of Statistics 74(1): 112-125.
12. Kachiashvili KJ, Mueed A (2011) Conditional Bayesian Task of Testing Many Hypotheses. Statistics 47(2): 274-293.