Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Mushref Algarni*1,2, Robert Stodilka1, Janine Riffel1, David Laidley1
Received: February 11, 2018; Published: February 23, 2018
*Corresponding author: Mushref Algarni, Department of Nuclear Medicine, London Health science, University Hospital, Schulich School of Medicine & Dentistry, Western University London, Ontario, Canada
DOI: 10.26717/BJSTR.2018.02.000795
London health sciences center is a frequent user of Lu-177 Dotatate for the treatment of neuroendocrine disease. We began using this radionuclide therapy as an in-patient procedure, where patients were released at 20 hours' post therapy administration with minimal restrictions. Over the course of 2013, we worked to transform this therapy into an outpatient procedure, where patients were released at 4-6 hours' post therapy administration with major restrictions. The previous methods and data we presented in December 17, 2013 were based on dose rates derived from cumulated doses measured over approximately 16 hours, and an assumption of Lu-177 clearance based on radioactive decay only. Since 2013, our hospital has gained more experience with Lu-177 Dotatate, enabling us to develop a better understanding of dosimetry. We describe new dose measurements, a new model we developed to describe our observations, and a revised schedule of patient release and restriction duration. Compared against previous measurements from 2013, our new measurements are of instantaneous (not cumulative) dose rates, and we now consider Lu-177 clearance to proceed both by physical decay and biologic excretion. Our new proposed model combines our experimental results with results from literature. The model will state the dose rate from time of discharge can be modeled as a decaying double exponential function [1-5].
Clearance processes are important to understand because they will allow us to predict dose rate from a radionuclide therapy patient after the patient is released from the hospital. Clearance kinetics for many radiopharmaceuticals can be described as having an early phase and a late phase. Early phase clearance is often dominated by protocol- and patient-specific variables that influence nonspecific uptake (for example: patient hydration, renal function). Conversely, late-phase clearance is usually from disease-specific uptake (for example: from a tumor). Many authors in literature model clearance kinetics using first-order approximations (first order rate kinetics), resulting in clearance equations with decaying exponential functions [6-10]. Following these examples, we propose the clearance of our radiotherapy product can be modeled as a summation of two exponential decay functions: [Equation 1]
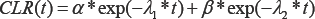
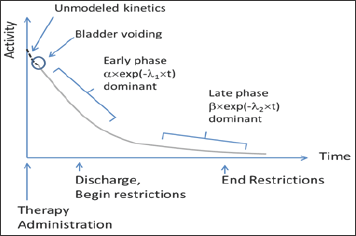
Where λ1 and λ2 describe the early phase and late phase effective decay constants, respectively; and α and β represent the respective proportions of our radiotherapy product governed by the early and late phase clearance processes. Note that the relationship between decay constant and half-life is λ =ln(2)/t1/2 where t1/2 is half-life (Figure 1).
Figure 1: In this figure, the radionuclide therapy is administered at time=0. At some point, the patient first voids their bladder, after which we begin to model the therapy product’s clearance kinetics. At first, clearance is rapid; and eventually clearance slows.
The total estimated effective dose (EEDTOTAL) received by an individual in close proximity to the patient is proportional to the area under the patient activity vs time curve, from [time = discharge] to [time = infinity] weighted by patient restrictions. We express this as follows: [Equation 2]
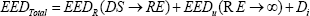
Where DS = discharge time and RE = restrictions end time. EEDR is the estimated effective dose received by the caregiver from discharge to end of restrictions, during which restrictions are in effect. We define it as: [Equation 3]
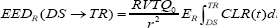
Where,
R [unitless] = dose reduction factor due to patient self-shielding (attenuation);
V [unitless] = dose reduction factor due to patient voiding after therapy administration;
г[uSv m2 / MBqhr] = specific gamma constant for Lu-177;
Q0[MBq] = initial amount of Lu-177 administered to patient;
r [meters] = distance between patient and exposed individual; ER[unitless] = restricted occupancy factor; and t [hours] = time.
EEDU is defined the same as EEDR, except the restricted occupancy factor, ER, is replaced with the unrestricted occupancy factor, EU; and the limits of integration are [time = RE] to [time = infinity]. Integrating Equation 2 is straight-forward, but leads to a lengthy equation that we omit here for brevity [10-15]. The term Di accounts for dose to the caregiver arising from internalized radionuclide's from the released patient, after NRC Regulatory guide 8.39. This is expressed as:
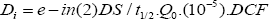
Where t1/2 is the Lu-177 physical half-life, 10-5 is the assumed fractional intake, and DCF is the dose conversion factor, taken as 0.05 [uSv/MBq]. What remains now is to assign numerical values to the variables. We have conducted an experiment to measure some of these values; whereas others are taken from literature, as will be described next.
Objective 2: Calculation of Voiding (V): We determined the fraction of radiotherapy product in the patient after voiding by comparing pre- and post-void dose-rate measurements in Table 1. We found the average ratio to be 0.87 [15-20]. The corresponding value in literature is 0.54. This void ratio is highly dependent on protocol design and time of voiding. All of our patients were instructed to void 1 hour post-administration of therapy.
Table 1: Calculation of Voiding (V) we determined the fraction of radiotherapy product in the patient after voiding by comparing pre- and post-void dose-rate measurements.

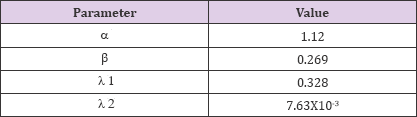
Objective 3: Parameters for Clearance Model CLR(t): The following values for CLR (t) parameters (Table 2). For interest, we note that the effective half-life associated with λ1 is t1/2 = 2.1 [hours], and λ2 is t1/2 = 91 [hours].
Table 2: CLR (t) parameters
Checking Model again Measurements: As a check of our results so far, we can plot our predicted dose rate for patients as a function of time; and compare this prediction with our measurements. Our predicted dose rate is given by:
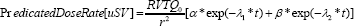
This predicted dose rate is compared with experimental measurements in Figure 2. For the case of 3700 MBq administered activities.
Figure 2: Dose rate for 3700 MBq Therapy at 1.9m.

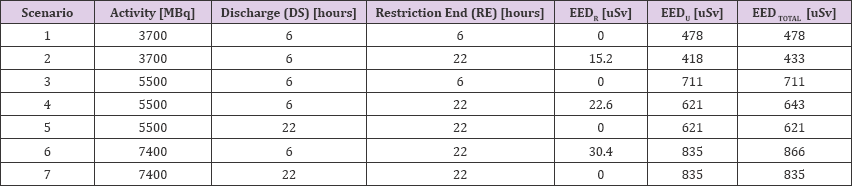
In all cases, restrictions are assumed to result in 0.25 occupancy (Table 3).
In our 2013 correspondence to you, we described an experiment where we measured cumulative doses from 14 patients. Dosimeters were placed in various locations in patients' rooms and measured over different time periods (up to 20 hours’ post therapy administration). During this time, patients moved around the room:from their bed to the bathroom, for example. We can compare this previous experimental data with our current model as follows:
Table 3: Model-Based Predictions of Eed.
a) In our previous study, the average activity administered was 5500 MBq, and the maximum was 7400 MBq.
b) We consider the longest cumulative dose integration time window in order to average patient movement: 4- 20 hours post therapy administration.
c) The dosimetry location we will select is the bottom of the patients' beds (near patient feet).
d) We will take this location as approximately "1 meter" away from the patient.
Table 4: Comparison of our 2013 data with our current mode. Thcorresponding calculations using our proposed model.

The same parameters can be entered into our model: an activity of 5500 or 7400 MBq, and a distance of 1 meter. We can use EEDR if we set DS=4 and RE=20, and restriction occupancy fraction to 1 [20-25] (Table 4).
From our 2013 data, the average dose measurement was 78 uSv (assuming the average activity of 5500 MBq). Our proposed model, assuming 5500 MBq, yields a dose of 101 uSv.
From our 2013 data, we have 0.18 uSv as a maximum dose (with 7400 MBq administered activity), and 140 uSv as the second highest recorded dose. Our model predicted 136 uSv. Our 2013 data shows variability, and there are differences compared with our proposed model ranging from 3% to 32%. Part of the variability and differences may be due to the patients of 2013 moving around their hospital rooms (their precise movement patterns over 20 hours were not monitored). However, overall we consider the 2013 experiment results and our model predictions reasonably close, especially considering we used two very different methods to arrive at dose. Our intention is to eventually use our new model to guide decisions for Lu-177 Dotatate patient restrictions and release from our institution. We would appreciate your thoughts on our proposal [25-28].


